设点与设线——一道解析几何题的解法探究

胡骏一 (江苏理工学院 231001)

在高三的一次练习中遇到一道解析几何题，笔者尝试从设点与设线这两个方向探究此题的解法．

图1

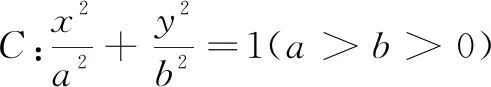
(2)思路1 (大三角形面积减小三角形面积)△PCD的面积很难直接用式子表示出来，由点P在第四象限，再结合图形观察到S△PCD=S△BCP-S△BCD，而△BCP和△BCD的面积比较好算．当然也可用S△PCD=S△ADP-S△ACD计算△PCD的面积．

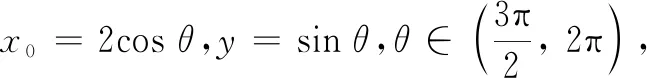
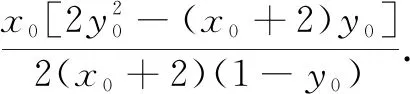
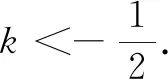
说明设直线PB方程来解决此题，最大的好处在于变量只有一个，即直线PB的斜率k，其他的计算都是常规套路．站在解题的视角来看，这道题设线应该要比上面的设点好解很多．

思路2 (用大三角形面积减四边形面积)如 图2，连结AB，观察到BC⊥AD，可知四边形ACDB的面积就是AD与BC长度乘积的一半，而△PAB中AB的长度是定值，这对于三角形的面积计算有帮助．

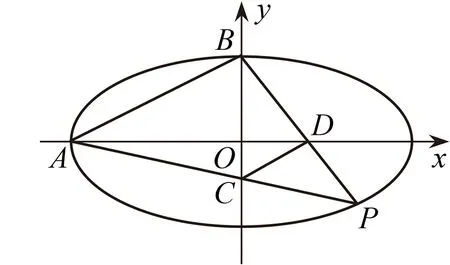
图2

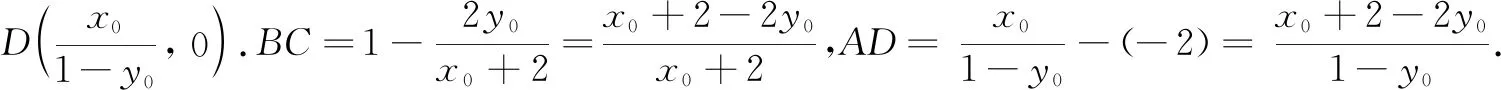
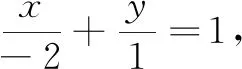
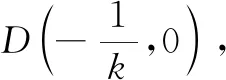
说明上述两个解法都解出四边形ACBD的面积为定值，又AB的长度为定值，进而只要研究点P到AB的距离最大值即可．