基于单线程的无锚点目标检测模型

李 浩，张晓强

（中国矿业大学信息与控制工程学院，江苏 徐州 221116）

0 概述

随着深度学习理论的发展和计算机性能的不断提升［1-3］，目标检测逐渐成为深度学习领域的热门研究方向，其实现方式为预测一幅图像的所有目标标注框以及对应分类。由于多数经典检测模型均是基于预设好超参数的锚点框，如RetinaNet［4］、SSD［5］、YOLOv3［6］等单阶段检测模型以及Faster R-CNN［7］等双阶段检测模型，因此研究人员普遍认为预设参数对目标检测模型至关重要，并证明了锚点的超参数设置可降低模型鲁棒性，并且显著增加模型参数调试的复杂度。自2018 年起，FCOS［9］、CornerNet［10］和CenterNet［11］等无锚点检测模型在无锚点的情况下预测物体，可避免调试锚点相关的超参数，但是获得的检测效果难以达到锚点检测模型的水平。

虽然锚点的设置使得目标检测领域取得显著进展，但是基于锚点的检测器仍面临诸多问题。在RetinaNet［4］中，锚点框的尺寸、比例与个数等超参数对该模型的平均精度影响较大，造成设置合理的上述参数较为困难。在设置合理的超参数后，由于锚点框的比例与尺寸在模型建立时必须固定，使得检测模型对形状变化较大的目标集的检测难度增大。同时，预制定的锚点框将会限制检测模型的鲁棒性与通用性，这是因为每遇到一个全新的数据集都需要重新设计锚点框的超参数以获得最优性能。为获得更高的召回率，一个基于锚点的模型需要在输入图像上密集铺置锚点框。比如在特征金字塔网络（Feature Pyramid Networks，FPN）［12］中，一幅图像的短边resize 为800 时，最终所需的锚点框数量将高达1.8×105，且多数锚点框在训练中均被标注为负例，而过多的负例将会加剧正负例数量的不平衡。全卷积神经网络（Fully Convolutional Networks，FCNs）［13］在语义分割［14-15］、深度估计［16］、关键点检测［17］、实例分割［18］以及全景分割［19］等密集检测任务获得显著效果。

近年来，无论模型是否使用锚点，预测头模块总是伴随着FPN，通过对FPN 中每张特征图对应的锚点框进行指定，特定的特征图仅预测特定大小范围的标签框。该预测结构的优点是可以使计算资源得到整合，有效提高检测精度以及模型对小型物体的召回率。但该预测结构与早期双阶段模型面对的问题类似，即从人类的视角来看，这种选择与屏蔽机制并不符合认知常识，并且无论是否是基于锚点的模型，特征金字塔结构的预测模式都会导致正例与负例的比例处于一个较低值，此时需要采取一些平衡正负例的措施，造成模型的冗杂度增加。为解决该问题，本文提出一种新的模型结构。该模型通过取消预设锚点参数环节和特征金字塔网络，避免与锚点相关的冗余并降低特征金字塔提取网络的权重，从而提高模型的鲁棒性。

1 全卷积单阶段单线程无锚点检测模型

1.1 无锚点预测头模块

本文提出的模型在训练阶段过程中，预测头模块的特征图标签制作过程舍弃了锚点与标签框匹配步骤，直接以预测头特征图的像素点为单位与标签框进行匹配。如图1 所示，预测头模块分为分类支路、检测支路与中心偏离支路3 个支路。

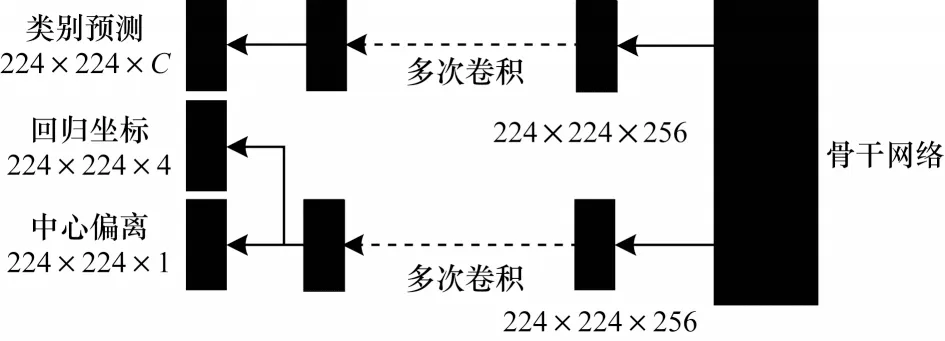
图1 预测头模块框架Fig.1 Framework of prediction head module

假设Fi∈ℝH×W×C为模型中一个预测头的特征图i，s是特征图到某一层为止的累加步长。一幅图像的标签框可以被定义为一个五维向量Bi，Bi=。其中，向量中的表示一个标签框的左上角与右下角对应的坐标，ci表示标签框的所属类别。C表示类别的个数，COCO 数据集的类别个数为80。对于特征图的每一个位置(x，y)，模型的坐标映射将其映射至初始输入图像对应的坐标位置([s/2]+xs，[s/2]+ys)，该映射得到的输入图像的坐标位置接近(x，y)坐标感受野的中心。

在基于锚点的检测器模型中，模型通常会输出几张特征图，这些特征图上的每一个坐标位置都会设置一个或多个锚点，而这些锚点的相关超参数与模型的预测结果相关联，锚点的超参数与目标签框的参数将会按照预设公式得到计算值。但是本文提出的模型中没有该步骤，其直接在每一个特征图的坐标位置回归标签框的坐标。即基于用于语义分割的FCNs［13］在舍弃锚点后，每一个坐标位置都会作为一个训练样本。取消锚点参数设置的原因如下：

1）目前主流的锚点超参数设置方式是基于特定数据集训练集的标签框形状进行聚类并计算得到。在模型进行检测时，由于检测集与训练集的数据分布相同，因此通常不会出现数据分布迁移的问题。但在实际应用中，训练集与预测对象的分布总是不同，而模型训练得到的权重往往与该组针对特定训练集的锚点超参数相关。针对利用单个图像中各个标签框与预测特征图中各个空间位置(x，y)的相对位置关系制作标签特征图问题，取消锚点机制可提高模型的通用性。

2）基于锚点的模型，通常标签特征图中的每个空间位置至少有9 个锚点，导致交并比得分计算过程中的数量较多，且密集的锚点铺设将会严重影响正负例标签的分布情况。损失计算与反向梯度传播过程中大量学习价值较低的负例降低了模型训练的效率，但基于空间位置的模型中每个空间位置只有一个损失计算对象，且正负例比例较锚点模型更高，这将大幅降低模型的运算量并提高训练效率。

3）研究实验表明，在增加了正例区域与中心偏离支路后，模型的检测精度与召回率均优于多数传统锚点模型。

1.1.1 正例区域原则

针对正例与负例的划分提出了正例区域原则，其规则为：取部分每个标签框的中心位置到该标签框4 条边的距离作为正例区域。假设原标签框高大于框宽，若原标签框的框高大于等于448，则取标签框高的1/3作为正例区域的高；若原标签框高大于等于224 小于448，则取标签框高的1/2 作为正例区域的高；若原标签框高小于224，则取标签框高作为正例区域的高。正例区域的宽遵循近似原则，不同之处是若标签框宽已经小于正例区域的高，则以标签框宽直接作为正例区域的宽。假设原标签框宽大于框高，则标签框宽首先按照上述规律计算获得正例区域的宽，接着换算正例区域的高，若标签框高小于正例区域的宽，则以标签框高直接作为正例区域的高。

若一张特征图中某个坐标位置(x，y)对应的原图位置落在任意一个正例区域内，则该位置被划分为正例，且其对应的类别c*是此正例区域对应的标签框类别；若一张特征图中某个坐标位置(x，y)对应的原图位置落在任意一个非正例区域的标签框内，则该位置将不会参与损失计算；否则此坐标位置将被归为负例，对应类别c*=0（背景）。正例区域选取方式示意图如图2 所示。

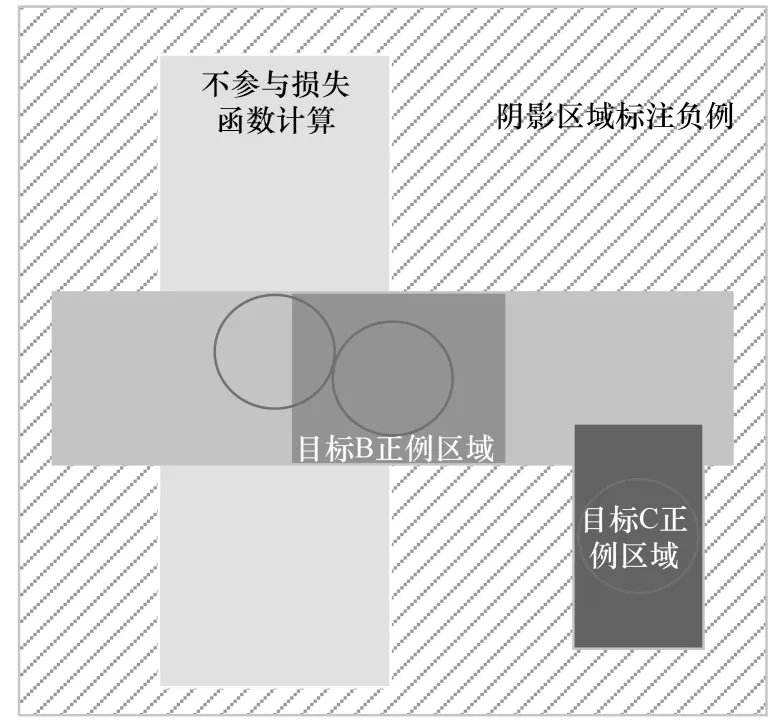
图2 正例区域选取方式示意图Fig.2 Schematic diagram of region selection method of positive example area

除了分类标签外，还可用检测标签的四维向量p*=(l*，r*，t*，b*)作为坐标位置的回归目标。四维坐标示意图如图3 所示。

图3 四维坐标示意图Fig.3 Schematic diagram of four-dimensional coordinates

(l*，r*，t*，b*)分别为坐标位置(x，y)对应的原图位置离标签框4 条边的距离。如果一个坐标位置同时落在多个正例区域内，则简单地将面积最小的正例区域作为其回归目标。正例区域原则上通过把图像中不同高宽比的标签框转换为形状趋向于正方形的正例区域，以调节正例坐标的分布，并将正例坐标集中在一起，且可获得以下2 个优势：1）正例区域原则降低了大型目标对应的特征图正例坐标个数，有效缩小了大型目标与小型目标在损失计算中所占比重的差别，且模型可对检测较为困难的小型目标投入更多注意力，不再将训练重心放在易检测物体上；2）只选取大型目标正例区域可有效避免关键位置被遮挡的问题（具体如图2 所示），关键位置是指以目标标签框中心为圆心的小型区域。实践证明该区域的检测结果通常是最优的，而如果不使用正例区域原则，目标A 的核心区域将会完全被目标B 的非核心区域所遮挡。坐标位置离标签框4 条边的距离如式（1）～式（4）所示：

1.1.2 中心偏离支路

中心偏离支路的作用是辅助筛除出低质量的预测框。研究表明，低质量预测框通常是由一些远离标签框中心点位置的坐标点所得，因此需尽可能降低坐标位置的分类预测值。在预测过程中，通过非极大值抑制（Non-Maximum Suppression，NMS）可筛除掉这类坐标位置，使得多数参与预测的坐标位置均接近目标物体中心位置。中心偏离是一个简单高效的筛除低质量检测框的手段。如图1 所示，仅需在预测头模块的分类支路或者回归支路中增加一个分支对中心偏离进行预测即可。此分支可用来计算预测点与对应目标框中心的距离，在给定标签位置(l*，r*，t*，b*)的情况下，中心偏离的回归目标S*计算方法为：

中心偏离的回归目标S*为0～1，损失函数将会被加入初始的损失函数中。在检测过程中，中心偏离预测分数将会乘以对应坐标位置的分类得分，并将得到的结果作为最终被使用的分类得分。因此，将会造成远离目标框中心的坐标位置对应的分类预测值大幅降低，而低质量的预测边框将会被NMS 清除，从而提高检测性能。

通过回归目标标签制作方式的更新与中心偏离模块的加入，本文提出的模型得以完全舍弃锚点，并以一种简单直接的方式进行训练，以获得更快的推理速度。

1.2 单线程骨干网络

将多个预测分支整合为单线程检测路线且不丢失小型物体的检测精度至关重要，一个可行的方法是尽可能地提高预测头特征图的分辨率，且为了避免模型过大而造成显存溢出，需使得骨干模型中的特征图分辨率尽量小。上述2 个要求看似存在相悖，但通过多次下采样之后再进行多次上采样的方式，可在减少模型参数量与计算量的同时，保证最终输出特征图和输入特征图的像素比达到一个较高的数值。在本文所提模型中，像素比达到了1∶4，则可避免由于像素丢失而导致位置信息丢失的问题。在减少模型中间部分参数量的同时，可将剩余的显存空间用来拓宽模型的深度，进而获得更深层的语义信息。不同于其他网络模型，本文模型使用沙漏形状的网络作为骨干网络，且不使用不同尺寸的特征图对不同大小的物体进行检测，省略了不同特征图制作训练标签时的信息判断过程。同时，模型构造时预测头的各个特征图之间的信息传递模块也将无需保留，最终模型只保留预测模块的3 个向量输出，从而节省了大量计算资源。

沙漏网络的内部结构如图4 所示。多个沙漏模块可以级联且方便扩展，从理论上可以无限制叠加，在本文提出的模型中，使用了2 个沙漏网络串联。沙漏模块先通过最大池化层以及一系列的卷积对输入特征进行下采样，再通过反卷积等一系列操作将特征图进行上采样直至恢复到原始分辨率。由于信息在最大池化层会存在一定的丢失，因此在沙漏网络中通过引入跳跃连接来弥补上采样模块中特征图损失的部分信息。该结构下的沙漏网络可采用一个整合归一的结构同时捕获特征图的全局信息与局部信息。

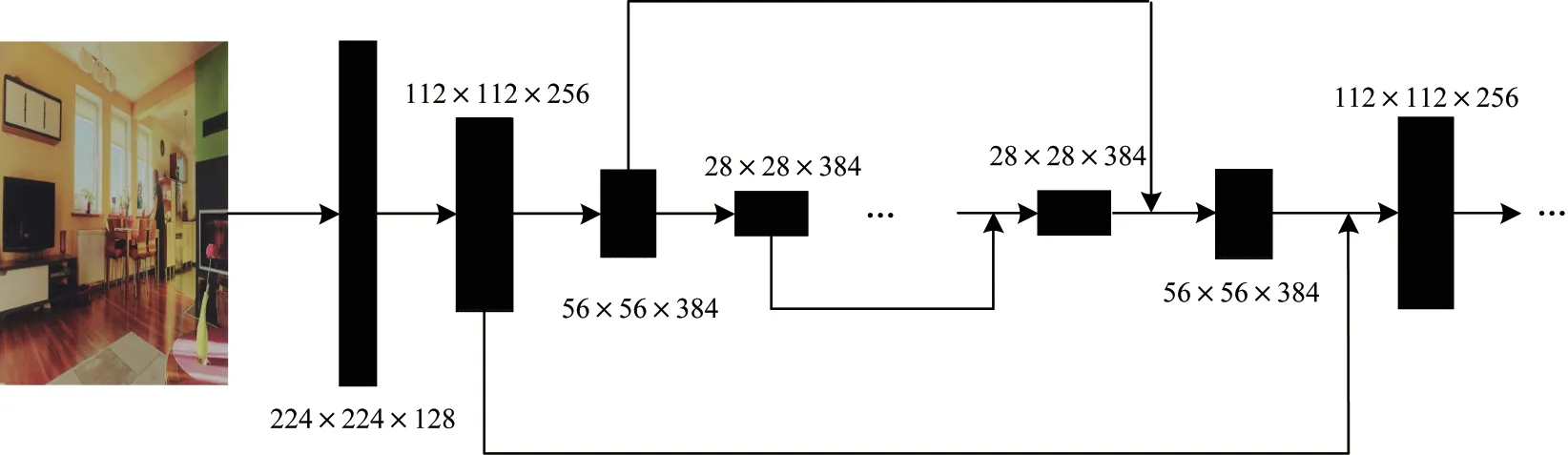
图4 沙漏网络的内部结构Fig.4 Internal structure of hourglass network

模型先通过2 个步长为2 的模块将特征分辨率降为原图的1/4，再将输出的特征图作为沙漏网络的输入。在如图4 所示的沙漏网络内部结构中，模型特征图的分辨率减半6 次，并按照256、384、384、384和512 的顺序改变其通道数。在达到最低分辨率时，沙漏模型通过最近邻上采样来逐步恢复其特征图边长，每次上采样前均会经过2 个残差网络模块，每个跳跃连接模块同样包括2 个残差模块，而拥有512 个通道数的特征图构成的沙漏网络中间位置则包含4 个残差网络。

通过把传统的骨干网络常用结构如Resnet［20］、Densenet［21］替换为沙漏网络，这样可以在骨干网络部分整合低阶几何（局部）信息与高阶（全局）语义信息。FPN 的核心作用也是整合这两类特征的信息，但区别在于以下2 个方面：

1）通常图像在每次下采样后都会损失部分信息，在后期即使进行特征融合也无法获得早期已损失的特征信息，因此早期在各个特征图之间加入信息传递模块。这是因为在加入信息传递模块后，下采样操作前的特征信息直接传递到模型后半部分，可有效保留早期损失的特征信息。沙漏网络在早中期特征提取阶段通过跳跃连接的方式对各个特征图之间的信息进行传递，尽可能地减少早期信息的损失，而FPN 主要作用于后期特征提取阶段，则早期阶段会不可避免地损失部分信息。

2）FPN 输出一组预测特征图（通常数量为3），假设未使用FPN 的模型预测特征图分辨率为7×7，则使用FPN 后分辨率变为7×7+14×14+28×28，极大地增加了制作标签特征图的计算成本。然而，由于骨干网络的特征图本身不直接参与标签制作，因此在骨干网络中进行特征整合可省略FPN 中多阶段的繁琐标签匹配过程。

当输入图像放大1 倍时，预测特征图的分辨率也仅为14×14，此时标签框制作的计算成本仍低于FPN 网络。但研究表明，通过沙漏网络对特征整合模块前置加上放大输入图像分辨率的联合操作，可获得高于FPN 网络的检测效果，且使用沙漏网络取代FPN 的作用，使得模型得以实现完全的全卷积单线程训练与检测。

1.3 模型结构与算法流程

模型的训练过程如算法1 所示。

算法1网络训练算法

图像输入至模型后通过2 次简单的卷积进行下采样操作，得到的特征图进入沙漏网络，并将经过多次沙漏模块提取后得到的特征图输入到预测头模块中，从而得到最终输出结果。模型最终输出层的每个空间位置预测一个80 维的分类标签向量c、一个四维预测框向量p=(l，t，r，b)与一个一维中心偏离向量。与文献［12］相同，模型没有训练一个复合类的分类器，而是训练了80 个二维分类器。在骨干模型得出的特征图的2 个分支上分别添加4 个卷积层，因为回归目标的值为正值，模型使用了exp(x)将回归分支的预测值x映射在(0，+∞)区间。损失函数如式（6）～式（9）所示：

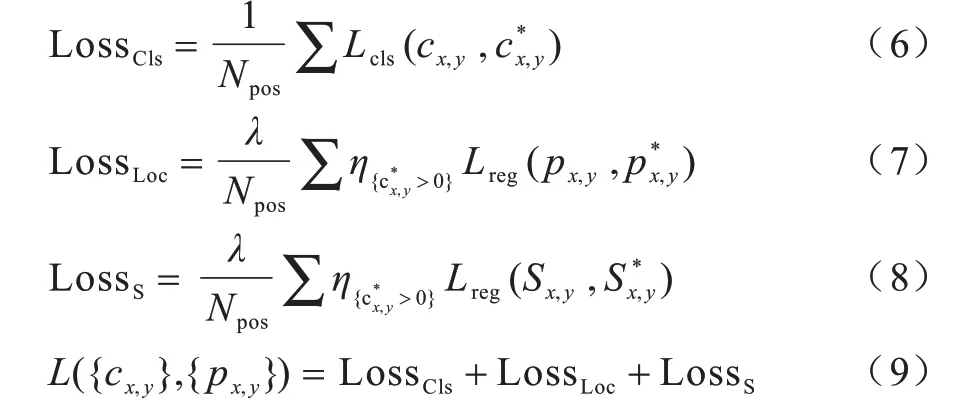
其中，Lcls为focal loss，而Lreg为GIOU loss，Npos表示正例的数量，λ是用于平衡分类与回归损失的比重超参数。Loss 的总值由特征图上所有坐标位置的损失计算而得出。η表示一个指示参数，若大于0 即对应坐标位置标签为正例，则η为1，否则为0。

模型的预测方式是输入一张图像，直接将其放入网络并获得最终特征图中每个位置的分类得分cx，y以及回归得分px，y。与文献［4］相同，参数选择cx，y＞0.05 的作为正例并通过式（1）～式（4）获得对应的预测框。

2 实验与结果分析

目标检测任务同语义分割任务类似，在逐像素全卷积预测中通过清晰简单的全卷积方式进行模型网络构建，并能获得与当前主流模型实现方式较为近似或更优的结果。

2.1 实验数据集

本文选择的实验数据集是基于大尺度目标检测基准数据集COCO，且COCO2017 与COCO2014 数据集对比如表1 所示。

表1 COCO2017 与COCO2014 数据集对比Table 1 Comparison of COCO2017 dataset and COCO2014 dataset

与文献［6，12，15］类似，本文模型使用COCO2017数据集进行训练与预测，COCO2017 比COCO2014拥有更多的训练图像且相应地减少了验证集的大小。模型没有对验证集进行微调，实验结果的预测性能基于验证集。

2.2 参数设置

模型使用随机梯度下降（Stochastic Gradient Descent，SGD）与动量Momentum 优化算法相结合，迭代2.7×105次，初始学习率为0.01，每批次有4 张图像，在2 个GPU 中训练。学习率为1.8×105与2.4×105时衰减为原来的1/10。权重衰减率设为0.000 1，动量Momentum 超参数设为0.9。模型使用Cornernet 的预训练权重初始化骨干模型。对于新增加的层，则参照文献［4］进行初始化，输入图像的尺寸统一缩放到896像素×896像素。

在检测过程中，模型通过对图像特征进行提取，获得每个坐标位置的预测坐标、预测类别与中心偏离，再通过点乘预测类别与中心偏离得到优化后的预测类别。接下来的后处理过程与文献［4］中的后处理方式相同，预测模式下的图像尺寸和训练模式的尺寸一致。

2.3 结果分析

实验将本文模型与其他经典模型的平均精度（Average Precision，AP）和平均召回率（Average Recall，AR）进行对比，结果如图5～图7 所示。在图5 和图6 中AP50 表示当检测框与标签框的交并比大于50%时预测正确，AP75表示当检测框与标签框的交并比大于75%时预测正确，APs、APm、APl分别表示模型预测小型、中型与大型目标的AP。在图7中，AR50、AR75以及ARs、ARm、ARl代表的含义与AP 同理。

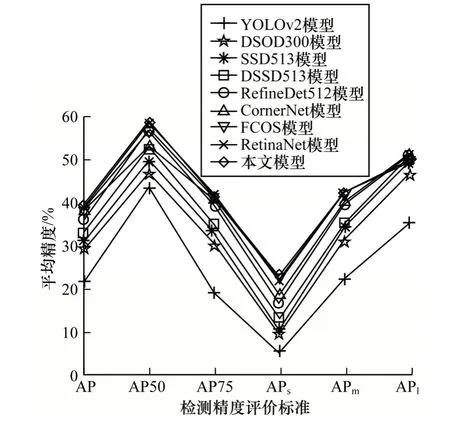
图5 单阶段检测模型的AP 对比Fig.5 AP comparison of one-stage detection models

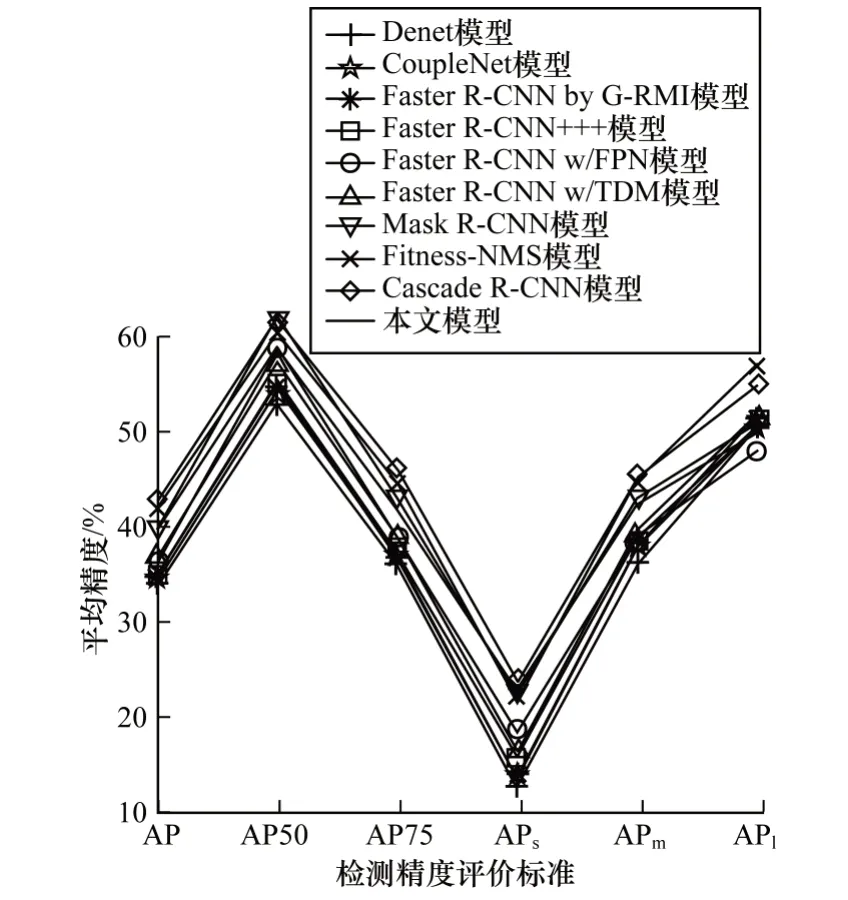
图6 双阶段检测模型的AP 对比Fig.6 AP comparison of two-stage detection models

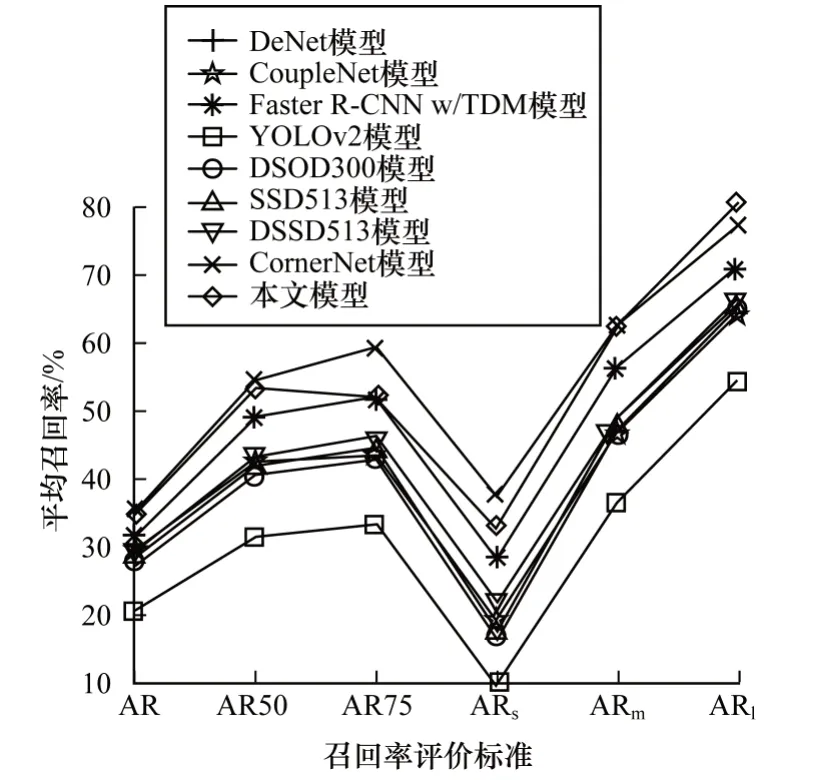
图7 9 种模型的AR 对比Fig.7 AR comparison of nine models

从图5、图6 可以看出，与基于锚点的经典单阶段检测模型（YOLOv2 与DSSD513）以及无锚点的新型单阶段检测模型（Cornernet 与FCOS）相比，本文模型的平均精度更优。虽然基于锚点的双阶段检测模型拥有比单阶段模型更复杂的结构与训练方式，但其精度水平与单阶段模型精度相当。在目标类别上，模型对大型目标的检测效率最优，其次是中型目标，而对小型目标的检测效果最差。

从图7 可以看出，单线程模型并未因为移除FPN而导致召回率明显下降，且其具有与FPN 模型相差不大的召回率，由此可见骨干网络的单线程构造可在一定程度上替代FPN 的功能。而在目标类别上，本文模型对小型物体的召回率相比其他模型好，这主要是因为通过正例区域原则增加了小型物体的预测损失在损失函数中的比重。若要继续提高小型物体的召回率，则需进一步对正例区域中手工选择的阈值超参数进行对比分析，以选择最优阈值。同时，还可以通过选取更多的阈值对取值区间进行细化，改进每个取值范围内标签框宽高与正例区域的宽高之间的映射关系。通过引入超参数软设置思想，对标签框宽高与正例区域的宽高构造连续函数，而不是简单地使用根据阈值分段的一次函数。

2.3.1 正例区域原则与中心偏离的效果

本文提出的无锚点检测模型使用正例区域原则与中心偏离技巧可以有效提高最终检测精度，正例区域平衡不同大小检测目标的对应坐标点的个数，并优化坐标点落点的分布。中心偏离赋给低质量的远离目标中心检测框较低的置信度，降低错误可能性较高的预测检测框通过非极大值抑制的几率。如表2 所示，正例区域原则与中心分离分支可以提高模型检测精度近4 个百分点，这说明正例区域原则与中心偏离支路可使得模型的精度超过了经典的基于锚点的模型Retinanet。

表2 正例区域原则与中心偏离对本文模型平均精度的影响Table 2 Effect of the principle of positive region and center deviation on the AP of the proposed model %

2.3.2 单线程效果

本文提出的沙漏型单线程网络结构具有与Resnet+FPN 结构模型相当的语义特征表征能力，且可节省大量的内存空间。节省的空间可以提高初始输入图像与最终用于检测特征图的分辨率，并进一步提升模型的特征提取与表征能力，从而保证了模型能够维持小型物体的预测精度。从表3 可以看出，沙漏网络+2 倍分辨率模型结构的检测精度高于Retinanet，而Retinanet 使用2 倍分辨率的特征图则会出现内存溢出问题。

表3 单线程网络对不同模型平均精度的影响Table 3 Effect of single-threaded network on the AP of the different models %

2.3.3 标签比例结果分析

在去除FPN 模块后，模型训练时的正负例比例得到平衡，模型正例标签在总标签个数占比如表4 所示。

表4 模型正例标签在总标签个数占比Table 4 Proportion of model positive example labels in total labels %

实验对本文模型与同样采用无锚点的FCOS 模型进行对比，其检测正例标签占总标签个数的比值远高于FCOS。正负例样本个数的不平衡会造成模型训练效率的降低，最终导致模型表现性能下降。虽然有方法可以减少这种比例不平衡造成的损失，比如设置正负比例标签输入模型的比例、增加正例标签对损失函数的影响权重等，但这些方法本身会引入大量的超参数和额外的计算量。而通过单线程的方法可降低模型本身标签的不平衡性，达到增加正例标签占比的效果。

2.3.4 推理速度对比

在模型推理速度方面，实验对本文模型与其他经典模型进行对比，结果如表5 所示。

表5 4 种模型的推理速度对比Table 5 Comparison of reasoning speed of four models ms

本文模型兼具较少计算量与较低模型复杂度的优势，使得预测图像的推理速度得到了提升。通过在1.1 节与1.2 节中对模型进行改进与精简，本文所提模型对每张图像的推理时间为149 ms，这主要是因为：1）模型没有采取现有常见的多阶段预测模块特征金字塔网络FPN，这种预测模式类似于双阶段检测模式，不符合人类视觉认知的方式，同时模块会增加计算量与权重参数；2）模型没有采取锚点可减少大量锚点的相关计算量。由此可见，本文模型的复杂度与推理计算量远低于传统基于锚点的FPN 预测头模型。

正例区域原则、中心偏离支路以及单线程构造网络使得本文模型的性能高于传统带有锚点超参数的单阶段检测模型，且模型复杂度远低于传统模型。虽然本文模型的预测精度为单模型单尺度测试，而部分对比模型的精度结果为多模型多尺度，但是该模型的总体预测结果仍优于对比模型。

3 结束语

本文提出一种基于单线程的无锚点模型，通过正例区域原则优化无锚点网络的标签特征图构造方式，加入中心偏离支路优化模型训练时权重的更新效率以及检测推理效果，并将骨干网络改造为单线程构造以减少模型的内存需求。实验结果表明，该模型可显著提高预测精度并加快推理速度。下一步将通过加入压缩激励模块和中间监督模块，解决特征提取效率较低的问题，进一步提高本文模型的预测能力。