一种新颖的基于混合不确定性的特征选择方法

2021-05-17苏婷婷

长春工业大学学报 2021年2期

苏婷婷, 胡明, 赵佳

(长春工业大学计算机科学与工程学院，吉林长春 130012)

0 引言

由于计算机行业与数据库技术飞速发展，在数据快速积累的情况下，数据挖掘技术成为当今研究热点[1]，人们通过对数据进行分析，从中获得具有更大价值的产品和服务。在数据中找出特征间的相关性，可以快速、高效地发现数据之间的内在联系，并有效地应用于相应领域，使得该领域得到最优解决方案。

近些年，数据挖掘技术已在各行各业不可或缺，原始数据集中特征相关性分析成了热门领域[2]。如何在看似不相关的数据中挖掘出其内在联系也是文中重点研究方向。特征的有效性可以使用特征选择算法来度量，特征选择可以提高实验结果的准确性,并降低所需计算成本。各个领域的数据集中包含了大量冗余特征或者不相关、无效的特征，特征选择算法通常被人们用来对数据做预处理工作，去除数据集中不相关、弱相关特征以及冗余特征，从而增强了数据质量以及实验结果的准确性。

特征间的相关性是特征选择领域里的热门问题[3]，而好的特征子集包括与类高度相关(可预测)，但彼此不相关(不可预测)的特征[4]。因此去除数据集中干扰特征,并找到数据集中的关联关系应用于该领域，是现在各个行业必不可少的技术。在海量数据中，快速获得有价值数据，并在这些有价值数据中找到数据之间联系，可以解决原始数据间的相关问题,并促进其有突破性进展，这也是文中所研究的重点问题。

近年来，大多数研究者更倾向于利用互信息来对特征间的相关性进行度量，比较经典的有Hanchuan Peng等[5]提出的基于互信息的特征选择：最大依赖、最大相关和最小冗余，简称mRMR，它在原始特征集合找到与输出结果相关性最大，但特征与特征之间相关性最小的一组特征。但是互信息的方法不能直接比较不同类型变量,且得出的结果具有较强的冗余性。Lei Y等[6]提出一种基于快速相关性的过滤性解决方案(FCBF)，通过对称不确定性方法有效删除高维数据中冗余和不相关的特征，挖掘出与类别变量最大相关的特征。但是该方法未能有效控制类别变量对数据集中特征间相关程度的影响，并没有做到对特征间关系的深度挖掘。

针对上述问题，文中设计一种对原始数据集之间的关联关系进行挖掘的SU-P方法。此方法基于对称不确定性(SU)来对数据间相关性进行度量，由于通过SU得到的特征子集存在很大的冗余性，则需要更深层次对数据集进行去冗余操作。为避免类别变量会对去冗余的结果造成影响，文中利用偏相关分析对特征子集进一步处理，并利用近似马尔科夫毯方法去除冗余特征，得到最终的最佳特征子集。

1 相关理论

1.1 特征选择

特征选择是数据的预处理过程，通常在数据挖掘、机器学习以及模式识别方面都有着不可或缺的作用[7-8]。特征选择主要是选择有效的特征子集，也就是说,去掉不相关和冗余的特征[9]，这样通过减少特征个数，从而使运行时间更短，大大提高了模型精度,并且特征选择后数据中特征值的数值没有发生变化。

特征选择方法分为包装法、嵌入法、过滤法[10-11]。包装法需要利用学习模型对特征子集进行分类评估，因此对大型数据集需要较高的计算成本[12]；嵌入法利用学习模型指导特征选择，并将特征选择作为训练中的一环，正则化方法就是嵌入技术之一，它可以连续收缩并自动选择特征子集[13]；过滤法将特征选择当成一个预处理的过程，根据数据中的特性对所选的特征子集进行评价，且独立于学习算法，因此计算成本低,且不会继承其他学习算法的偏差，还能快速方便地分析大型数据[14]。过滤法独立于模型本身，其结果比包装法更具有普适性，计算性能优于包装法。包装法和嵌入法与直接算法相关，且更易于获取特征子集，但是它们根据具体的学习算法而定，鲁棒性较差，容易过拟合，计算复杂度较高，所以不适合于大规模数据集[15-16]。相对于包装法，过滤法要快得多，可应用于特征数量非常多的大型数据集，文中SU-P方法也主要依赖于滤波方法。

1.2 理论基础

在信息论中，通常用熵来作为随机变量不确定性的度量，熵越高，不确定性越高。若随机变量X的概率密度函数为p(x)，那么X的信息熵为

H(X)=-∑p(x)log2p(x)。

(1)

服从联合分布为p(x,y)的一对离散型随机变量(X,Y)称为联合熵(复合熵)，定义为

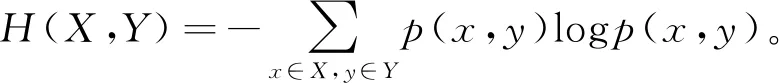
(2)

在两个随机变量中，其中一个随机变量在给定的另一个随机变量的条件下的熵为条件熵。在已知随机变量Y的情况下，随机变量X的条件熵H(X|Y)可推导为

H(X|Y)=H(X,Y)-H(Y)。

(3)

互信息定义是一个随机变量由于另一个已知随机变量而降低的不确定性，结合前几步可得

I(X;Y)=H(X)-H(X|Y)。

(4)

对称不确定性(SU)是标准化的互信息，有关对称不确定性的公式为

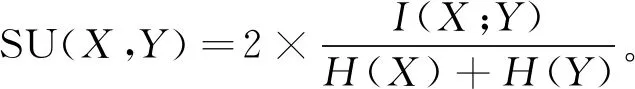
(5)

2 SU-P特征选择方法

由于互信息标准偏向于多值的特征，对称不确定性(SU)作为互信息归一化的表现形式，可克服其缺点。由下式计算特征与类别之间相关性，

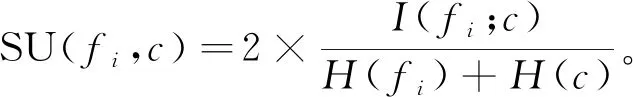
(6)

假设数据集S中有n个特征和m个类，设F={f1,f2,…,fi,…,fn}，F表示数据集中特征集合。C={c1,c2,…,ck,…,cm}，C表示数据集中类别集合。计算数据集中特征与类别之间的SU(fi,c)值，其值越大,则相关性越强。设定阈值σ,保留SU(fi,c)>σ的特征，根据其值将保留的特征降序排列方式,并将其插入特征子集列表中，构成与相应类别相关的特征子集F={f1,f2,…,ft}。

为了得到更精确的特征子集，还要进一步删除特征子集中冗余特征。利用偏相关系数对数据集进一步处理，这样不仅解决冗余性问题，还可以在计算特征间相关性时剔除类别的影响。公式如下

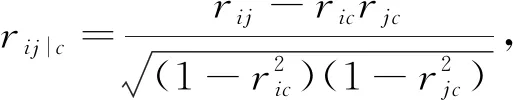
(7)

式中：c----类别变量;

rij|c----控制类别c时特征i和特征j之间的相关系数。

根据下式过滤特征子集F={f1,f2,…,ft}中冗余特征,

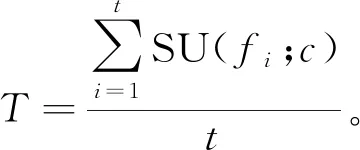
(8)

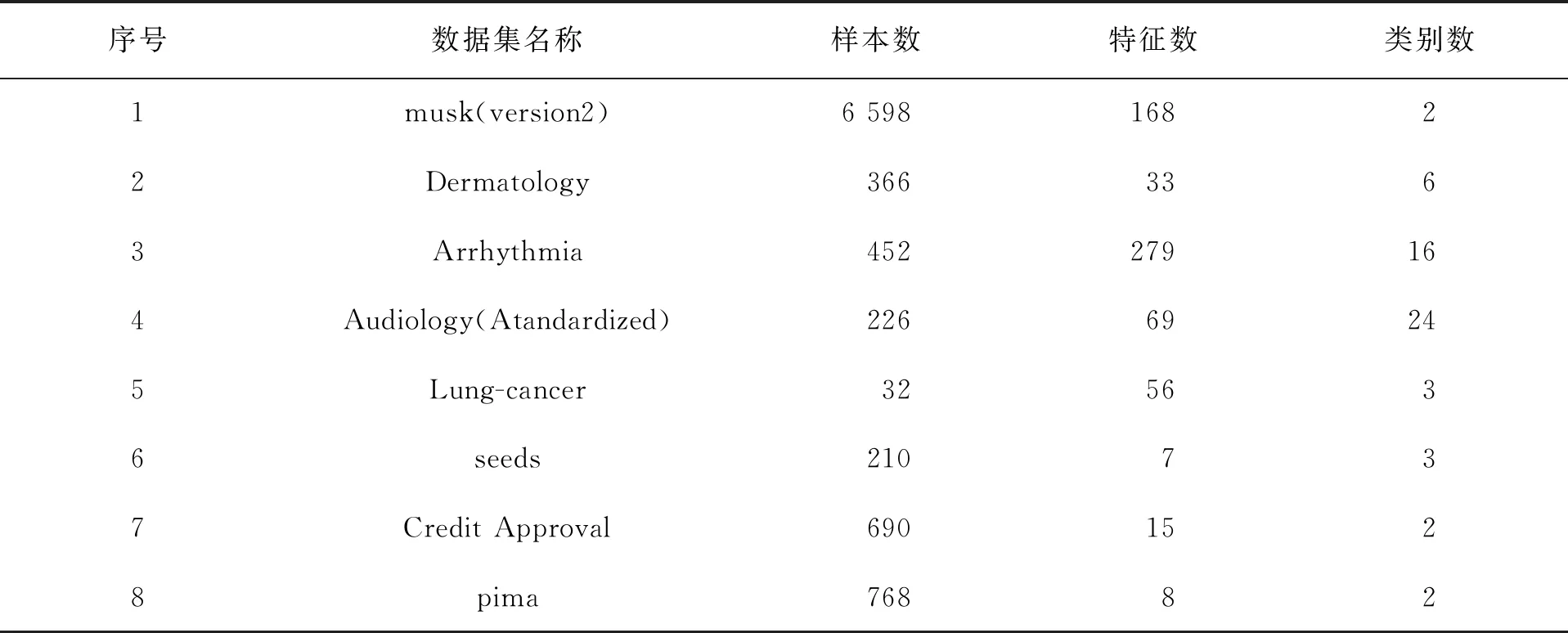
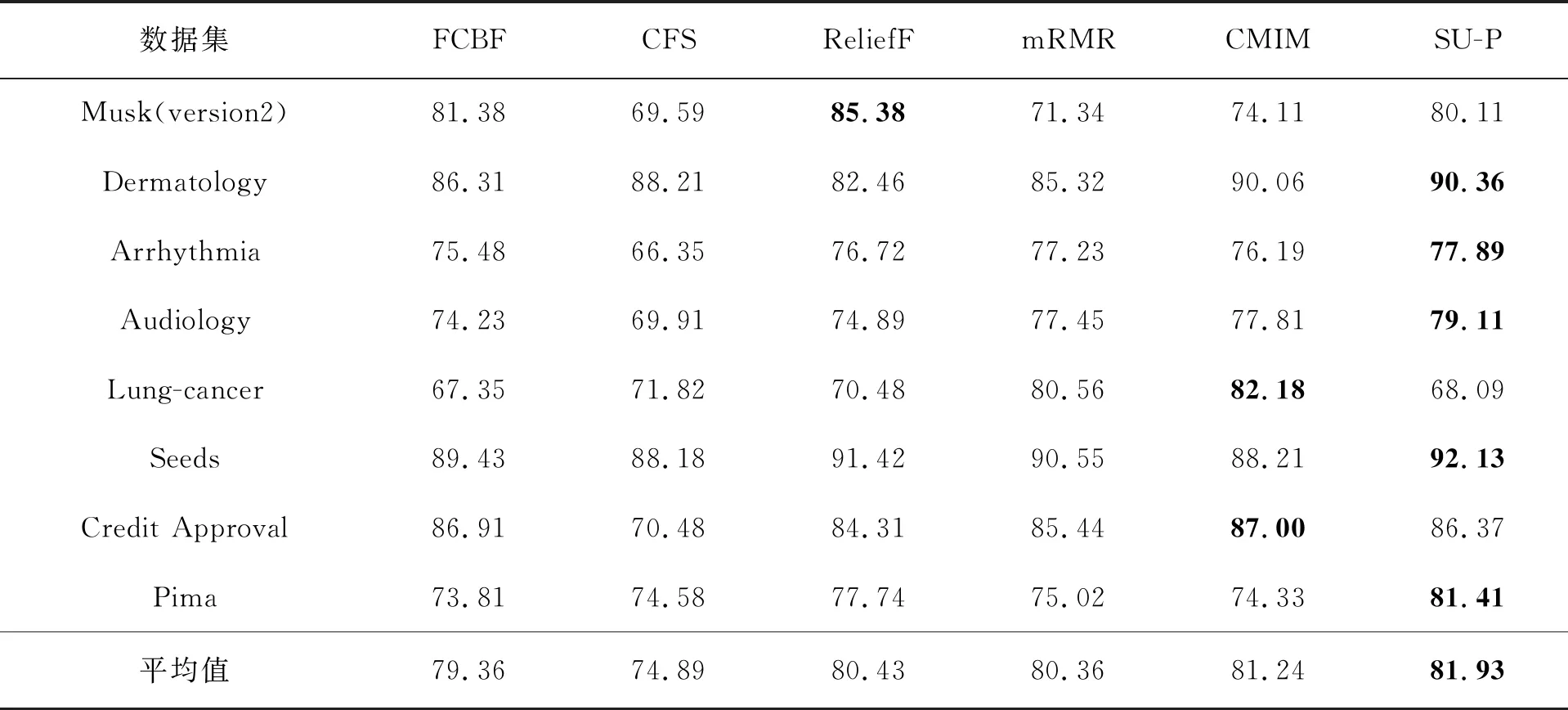
在给定类别c的情况下，计算特征fi与fj之间是否相互独立，通过式(7)来衡量。即将特征子集中排序第一的特征f1作为对比特征，通过依次计算特征子集里特征之间的相关性，若r12|c>T，则去除冗余特征f2(因为特征子集为降序排列，则f2与类的相关强度小于f1与类的相关强度)；若r12|c

3 实验结果及分析

通过将SU-P算法分别与FCBF、CFS、ReliefF、mRMR以及CMIM 5种特征选择算法在NBC、SVM以及KNN分类器上取得的分类准确性进行对比，证明SU-P特征选择算法的有效性，并用8个不相同的数据集来实现模拟比较实验。其中，数据集均是来自UCI机器学习存储库。关于8个数据集的相关信息分别为数据集名称、样本数、特征数和类别数。测试样本数据集的相关描述见表1。

表1 测试样本数据集的相关描述

从表1可知,这8个数据集所包含的样本数、特征数以及类别数各不相同。样本数最多为6 598个，最少为32个;特征数最多为279个，最少为7个;类别数最多为24种，最少为2个。由于以上8个数据集常被用于特征选择算法之中，所以,文中也利用这些数据集来验证实验结果的准确性。六种算法在NBC分类器上的分类准确率见表2。

表2 六种算法在NBC分类器上的分类准确率 %

表2给出了使用6种特征选择算法后，8个数据集在NBC分类器上的分类准确率，并用“平均值”表示8个数据集通过不同算法得到的平均分类精确度。

通过对比观察6种特征选择算法的分类准确率结果发现，虽然在Musk数据集中，SU-P算法的分类准确率要稍微低于FCBF算法与ReliefF算法，但是明显高于其他几种算法。在Lung-cancer数据集中,SU-P算法分类性能低于其它4种特征选择算法，但是其准确率要高于FCBF算法。在Credit Approval数据集中,SU-P的准确率尽管不是最好的，但是与在该数据集上表现最好的CMIM算法的准确率相接近。在剩余的5个数据集中可以看出,SU-P算法效果要优于其它5种算法。因此综合分析8个数据集的结果，可以得出文中提出的SU-P算法在大多数情况下比其它5种算法在NBC分类器上的准确率更高。六种算法在SVM分类器上的分类准确率见表3。

表3 六种算法在SVM分类器上的分类准确率 %

通过对比发现，Dermatology、Arrhythmia、Audiology、Credit Approval、pima这5个数据集中，SU-P算法的分类准确性要明显高于另外5种特征选择算法。在另外3个数据集中虽然分类效果不是最好的，但是准确率与其它几个算法在数据集上非常接近，且SU-P的平均准确率也要明显高于其他5种特征选择算法。总的来说，SU-P算法在SVM分类器上大多情况下要好于另外几个特征选择算法。

六种算法在KNN分类器上的分类准确率见表4。

表4 六种算法在KNN分类器上的分类准确率 %

在表4中仍然可以看出SU-P算法的有效性，在大多数数据集中SU-P算法的分类性能要优于其它几种对比算法，而只有在两个数据集中，SU-P算法在KNN分类器上的分类准确率要低于取得最高分类准确率的算法，但是其结果在6种算法中并不是最差的。总之，通过以上3个分类器中的对比情况可以看出SU-P算法的有效性。