基于二维分块自适应阈值小波的地铁塞拉门数据压缩

(西南交通大学电气工程学院，四川成都，610000)

随着我国高速地铁列车的蓬勃发展，地铁列车运行安全成为人们关注的焦点。地铁塞拉门作为直接关系乘客安全的核心部件，对地铁列车运行安全有着最为直接的影响[1-2]。为提高地铁列车运行的安全性和可靠性，车门预测与健康管理PHM(prognostics health management)日益受到重视。在塞拉门PHM 诊断中，塞拉门开关门过程中的电机电流数据蕴含了丰富信息，是塞拉门PHM相关研究基础。由于采集频率高，开关门过程频繁，产生的海量数据难以直接保存，因此，研究适合于实际工程的数据压缩方法已成为地铁塞拉门PHM的迫切需求[3]。

国内外学者对数据压缩方法进行了大量的研究，涉及多个领域，鉴于目前当前领域相关研究较少，塞拉门开关门过程数据本质仍是电机电流数据，因此，可借鉴电力系统录波、电能质量监测数据和心电图数据等领域的数据压缩方法。黄纯等[4-5]采用FFT 对数据进行压缩，取得了一定效果，但该方法是基于信号平稳、线性的假设，面对非线性平稳信号具有一定局限性。SANTOSO等[6-12]采用基于小波系数阈值压缩方法，将数据分解为小波系数，通过设置阈值，去除冗余数据，实现数据压缩。该方法有效处理了非线性、非平稳信号，展示了小波变换在数据压缩中的优越性。但其难以去除周期性数据周期间的冗余，导致压缩比受到很大限制。赵艳粉等[13-18]将多组周期性的一维数据进行了二维组合，使用二维小波对组合后的二维数据矩阵进行压缩试验，降低了数据周期间的冗余，进而极大提高了数据的整体压缩率，证明了相同条件下二维压缩算法的优越性。但由于其采用全局阈值的处理方式，在面对塞拉门电机电流这样高低幅值变化较大的数据时难以兼顾压缩率和压缩信号的重构精度。

针对以上问题，本文作者提出一种新的压缩算法。将塞拉门一次完整开关门过程电机电流数据作为一个周期，多个周期数据排列为二维矩阵，归一化后转换为二维灰度图像，使用二维小波变换对其进行压缩。压缩过程中，根据灰度图像各部分特点对二维灰度图进行自适应分块，根据预设阈值和压缩率等自动调整各块的小波阈值放大系数。分块之后的图像采用不同的阈值进行压缩。相对于传统二维小波压缩所使用全局阈值处理方式，二维分块自适应阈值小波压缩方法，在具备高压缩的同时，还能尽可能多地保留原始数据的细节，为日后地铁塞拉门故障诊断奠定了良好的原始试验数据基础。

1 二维小波压缩

小波变换是一种对信号的时间-频率的变尺度分析方法，在短时傅里叶的基础上，小波变换通过伸缩平移运算对信号进行多尺度细化，能自动适应时频信号分析的要求。通过小波变换，原始信号被近似系数和细节系数替代，可以在保证重构信号误差的前提下减少数据的存储空间，从而实现数据的海量压缩。

1.1 二维小波变换

二维小波变换是一维小波变换的推广，与一维小波变化不同的是，二维小波变换是对二维数据(行和列)进行处理。图1所示为金字塔式分解示意图。从图1可以看出：经过二维小波变换，可以将二维数据分为低频(LL)、水平高频(HL)、垂直高频(LH)以及斜线高频(HH)4部分。二维小波函数以及尺度函数可以通过一维小波函数以及尺度函数经过张量积变换得到[19]。

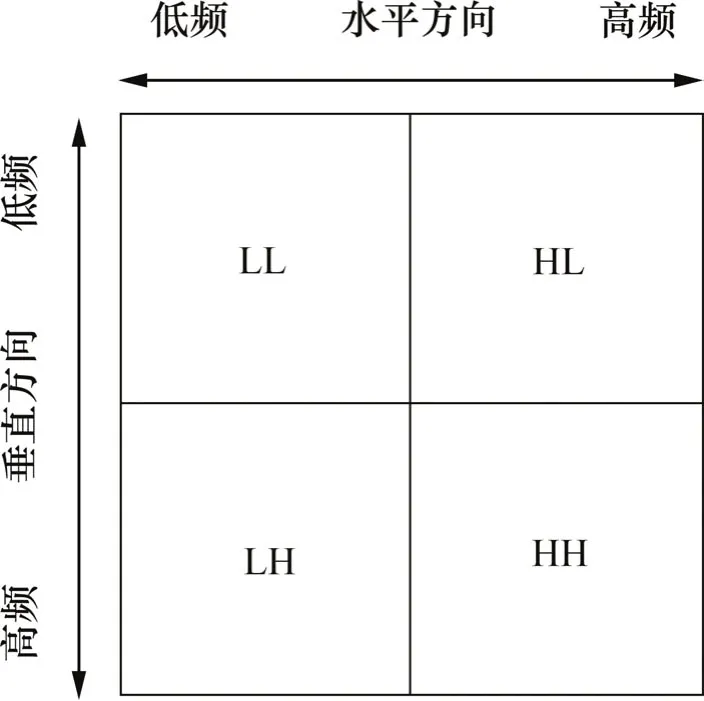
图1 金字塔式分解Fig.1 Pyramid-like multi-resolution structure

对于二维小波变换，其尺度函数为

式中：φ(x)和φ(y)为一维小波变换的尺度函数。其3个小波函数为

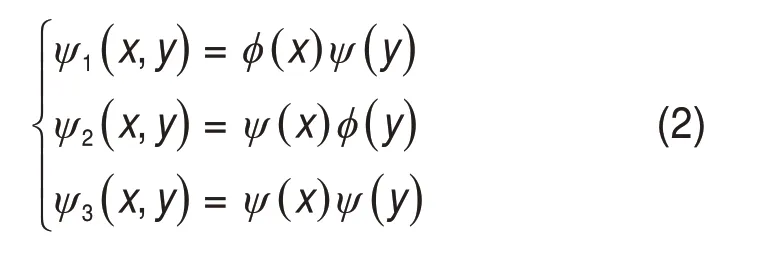
式中：ψ(x)和ψ(y)为一维小波函数；ψ1(x,y)，ψ2(x,y)和ψ3(x,y)分别为水平、垂直以及斜线高频部分。二维小波分解步骤如图2所示。

图2 二维小波分解步骤Fig.2 2D wavelet decomposition step

图2中：CA,j为第j层分解的低低频系数；CV,j+1为第j+1 层分解的低高频系数；CH,j+1为第j+1层分解的高低频系数；CD,j+1为第j+1层分解的高高频系数；“1↓2”为二倍抽取；Lo-D为低频滤波器；Hi-D为高频滤波器；行卷积与列卷积分别表示滤波器进行行卷积与列卷积运算。

二维小波重构的过程即为上述过程的逆变换，通过二维小波重构，可以将小波变换得到的小波系数还原为原始信号。

1.2 二维小波压缩流程

通过对二维数据进行二维小波变换可得到二维小波系数，对二维小波系数进行处理可以达到压缩的效果，其压缩过程如下：

1)根据选取的小波基以及分解层数对原始信号分解得到小波分解系数；

2)根据实际压缩需要(压缩比、误差比等性能指标)对分解后的小波系数选取适当的阈值；

3)根据实际情况，选用不同的阈值运算对得到的小波系数进行处理，去除冗余数据，得到新的小波系数；

4)对新小波系数进行二维小波重构，即可得到压缩后的重构信号。

2 地铁塞拉门数据特点及数据预处理

2.1 地铁塞拉门数据特点

图3所示为地铁塞拉门多次开关门数据三维示意图。从图3可以看出：地铁塞拉门开关门数据具有周期性、幅值变化大等特点。其周期性可以使数据按照周期固定整数倍截断，将截断的相同长度的数据并列排列获得二维数据。其幅值变化大的特点决定了其数据不能采用以往在小波压缩中使用全局阈值的方式。

图3 多组开关门数据Fig.3 Multiple sets of door data

2.2 地铁塞拉门数据二维表示

地铁塞拉门数据主要是对电流波形采样的一维数据，不能直接使用二维小波进行压缩。因此，需要对一维的数据进行变换。根据地铁塞拉门数据特点，本文将一次塞拉门开关门数据作为1个周期，将40组开关门数据按200 000个采样点进行截断，将截断的相同长度的数据并列排列获得二维数组，之后通过归一化，将得到的二维数组转换成二维灰度图像。对于平滑图像的压缩，任何压缩工具都可以表现出更好的压缩性能[20]。

图4所示为40 组数组转换得到的灰度图。从图4可以看出：转换为二维灰度图在行和列上的变换比较小，有利于信号的分解。地铁塞拉门数据采集的频率很高，采集间隔小。因此，所形成的二维矩阵在对角线方向上的变化也比较稳定。

图4 二维数据灰度图Fig.4 Two-dimensional data gray images

3 二维自适应阈值小波压缩算法

3.1 自适应分块

由于小波压缩时的阈值根据数据的幅值进行设定，而原始数据幅值变化大，若采用不分块处理，全局阈值只有1个，压缩时若阈值较小，则重构精度高，但压缩率低，反之若提高了压缩率则无法保证足够的精度[21]。

在保证过程数据具有较高压缩率的前提下，尽可能多的保留高幅值和低幅值的数据，使数据重构误差保持在允许范围内。现对经过归一化后的原始数据进行分块处理，设采集到的地铁塞拉门开关门数据，每个周期采样n点，共有m个周期。将每个周期的n个数据作为二维数据的1 行，将m个周期的数据按照顺序进行排列，即构成了1个如式(3)所示的m×n的二维数据矩阵。

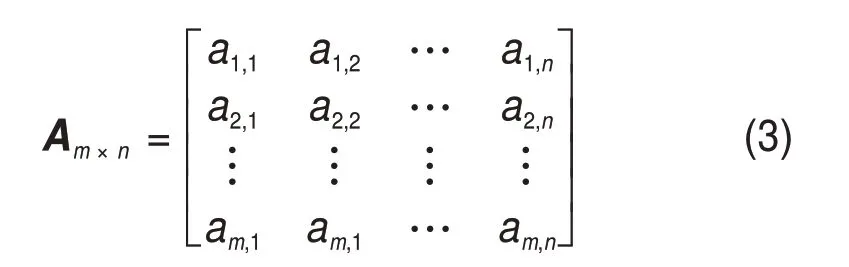
求取每一行的平均值得到Bm。

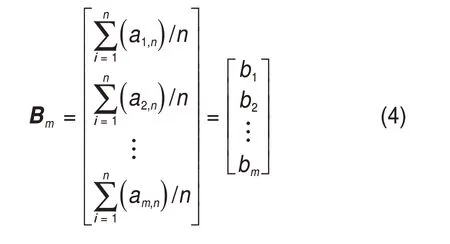
对形成的矩阵中的元素进行判断，当某一段元素的最大值最小值之差没有超过预设阈值Q时，该部分的数据视为1个数据块，当获得分块的块数以及分块的位置时，即可对获得的灰度图进行分块处理。

3.2 阈值处理

阈值选取是地铁塞拉门数据压缩的核心问题，目前阈值选取的方法众多，本文选择文献[22]中使用的通用阈值法，此方法与其他阈值选取方法相比，具有自适应性强、计算量小等特点，其计算公式如下：

式中：t为阈值；j为尺度；σ为噪声强度；K为该尺度下小波系数个数；γ为阈值放大系数。

当阈值确定之后，需要对其进行阈值运算。阈值运算分为：1)硬阈值，即将小波系数绝对值与给定的阈值进行比较，当小波系数绝对值大于或等于阈值时，系数保留原值，若小于阈值时，小波系数取值为0；2)软阈值，如式(6)对于给定的阈值，进行软阈值变换。

式中：c为小波系数。

软阈值法具有自适应光滑的特性，适合于信号去噪以及图像等要求自适应光滑特性的应用，但是，在采用相同阈值的情况下，硬阈值要比软阈值获得更小的均方误差。本文目的在于在获得高压缩的情况下，还能获得较小的均方误差，因此，选用硬阈值法对小波系数进行处理。

3.3 二维分块自适应阈值小波压缩算法

针对数据高低幅值不同不能采用全局阈值的问题，本文采用二维分块自适应阈值小波压缩的新方法，具体流程示意图如图5所示。

图5 二维压缩算法Fig.5 Two dimension data compression method

二维压缩算法压缩步骤如下。

1)前期数据准备。即使用数据采集卡采集地铁塞拉门开关门数据，之后将采集到一维地铁塞拉门数据进行二维表示，构成二维矩阵，经归一化将电流幅值表示为图像的灰度，得到二位灰度图像。

2)自适应分块。灰度图表示后的数据需通过预先设置的阈值以及相关限制条件对其进行分块，分块之后的灰度图像应具备相似的特征。

3)二维小波压缩与阈值修正。针对分块后的数据，分别选取不同的优化后的阈值，以获得尽可能大的压缩比，同时将误差限制在一定范围内。之后对每块灰度图各自进行二维小波压缩。通过将得到的小波系数进行保存对比预先计算的压缩率、均方误差、信噪比等判断与否，进行阈值修正，直至其压缩率达到预期的压缩率，最终完成数据压缩。

4 实验结果与分析

4.1 实验环境

本文实验数据来自江苏某地铁车辆现场采集的地铁塞拉门开关门实测数据。随机选用40 组数据进行测试，其余数据用于验证。计算机配置如下：处理器采用Intel(R)Core(TM)i5-8265U-CPU@1.6 GHz；内存为8 GB。程序在MATLABR2018A6 4bit条件下运行。

4.2 压缩性能指标

为衡量重构信号精度，本文选取4个评估参数对压缩算法进行评估[23-25]。

1)压缩率(compression ratio)CR为

式中：Nin为原始信号；Nout为压缩后最终保留的小波系数。通过压缩率，可以判断算法的压缩性能。

2)信噪比(signal to noise ratio)NR为

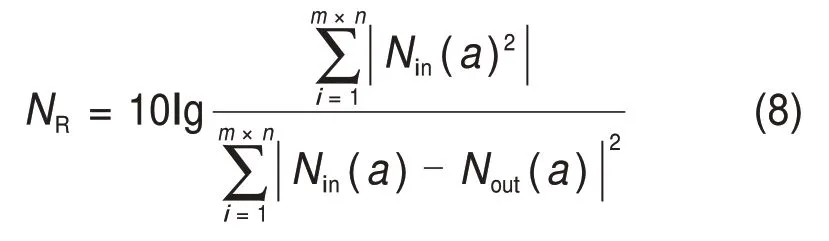
通过信噪比，可以判断压缩对信号失真的影响，信噪比越大，压缩对信号造成的失真越低。

3)均方误差(mean-square error)eMSE为

通过均方误差，可以判断压缩产生误差的相对大小，均方误差越大，其产生的相对误差越大。

4)平均绝对误差eMAE为

平均绝对误差可以避免误差相互抵消的问题，因而可以准确反映实际预测误差。平均绝对误差越大，其实际预测误差越大。

4.3 实验结果与分析

根据文献[26-27]对小波基与分解层数进行选择，通过对比试验，本文选用db3 小波作为小波基，分解层数取4。使用硬阈值法对原始信号进行压缩试验，当采用相近数据压缩率时(1.52%左右)，使用自适应分块法将数据分为17 块，每块的阈值放大系数如表1所示。

表1 各块放大系数γTable 1 Amplification factors of every segments

原始数据经过压缩算法压缩后，采用不同方式处理得到的重构波形结果及其局部细节放大图分别如图6和图7所示。使用文献[17]中提及的不分块全局阈值二维离散小波压缩算法与文献[24]中的二维DCT 压缩算法作为对比实验。各项参数对比结果如表2所示。

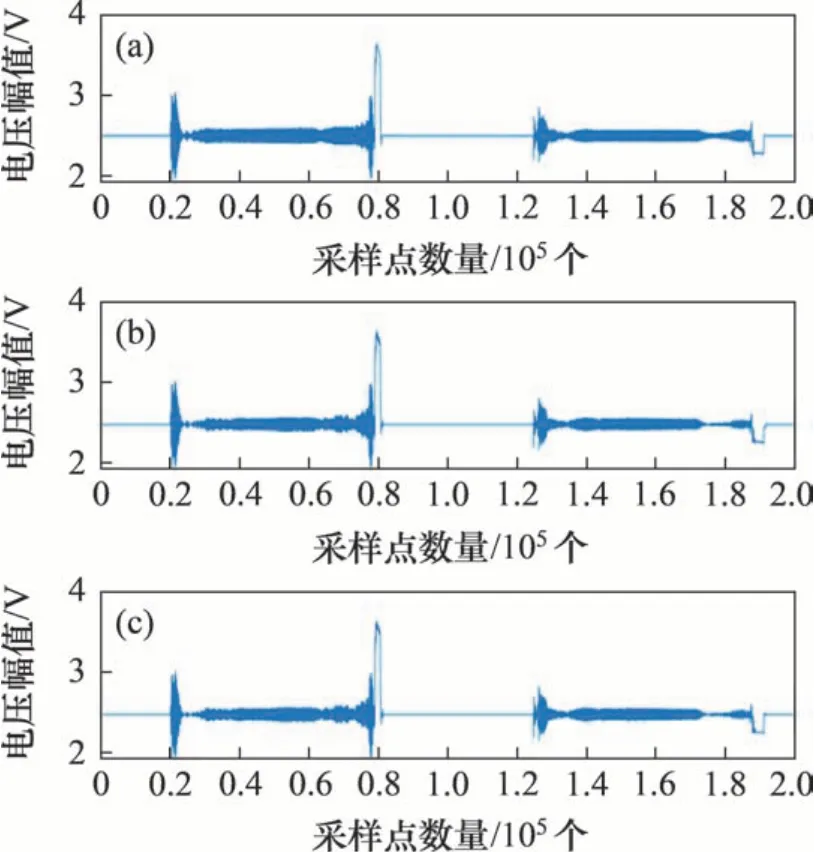
图6 原始信号及重构信号波形Fig.6 Original signal and reconstructed signal waveform

从图7和表2可以看出：二维DCT压缩算法可获得较高的信噪比以及较小的均方误差，但其压缩率较低，因此不适宜于地铁塞拉门数据压缩。而在压缩率(约1.5%)、信噪比(约43 dB)、均方误差(约0.7%)、平均绝对误差(约1.2 V)相近的情况下，采用分块自适应阈值分块的重构信号在波形幅值较小的区域，细节部分得到了很好的保留。相对于传统的方法，本文在幅值较小的区域可以保留更多的时频细节信息，系统的局部失真度更小。

表2 不同算法实验结果对比Table 2 Comparison of experimental results by different algorithms

图7 原始信号及重构信号局部细节放大图Fig.7 Enlarged view of original signal and partial details of reconstructed signal

为了进一步验证本文算法，采用图8所示实测的不同状态地铁塞拉门开关门数据进行试验，包括采集的A相开关门数据、B相开关门数据、C相开关门数据、单独A 相关门数据、B 相关门数据、C相关门数据、A相开门数据、B相开门数据以及C相开门数据，结果如表3所示。

从表3可以看出：在不同状态下，当信噪比约为43 dB、均方误差约为0.7%时，使用本文算法其压缩率基本保持在1.5%左右。基于分块自适应阈值小波压缩的方法效果稳定，具有一定的实用价值。

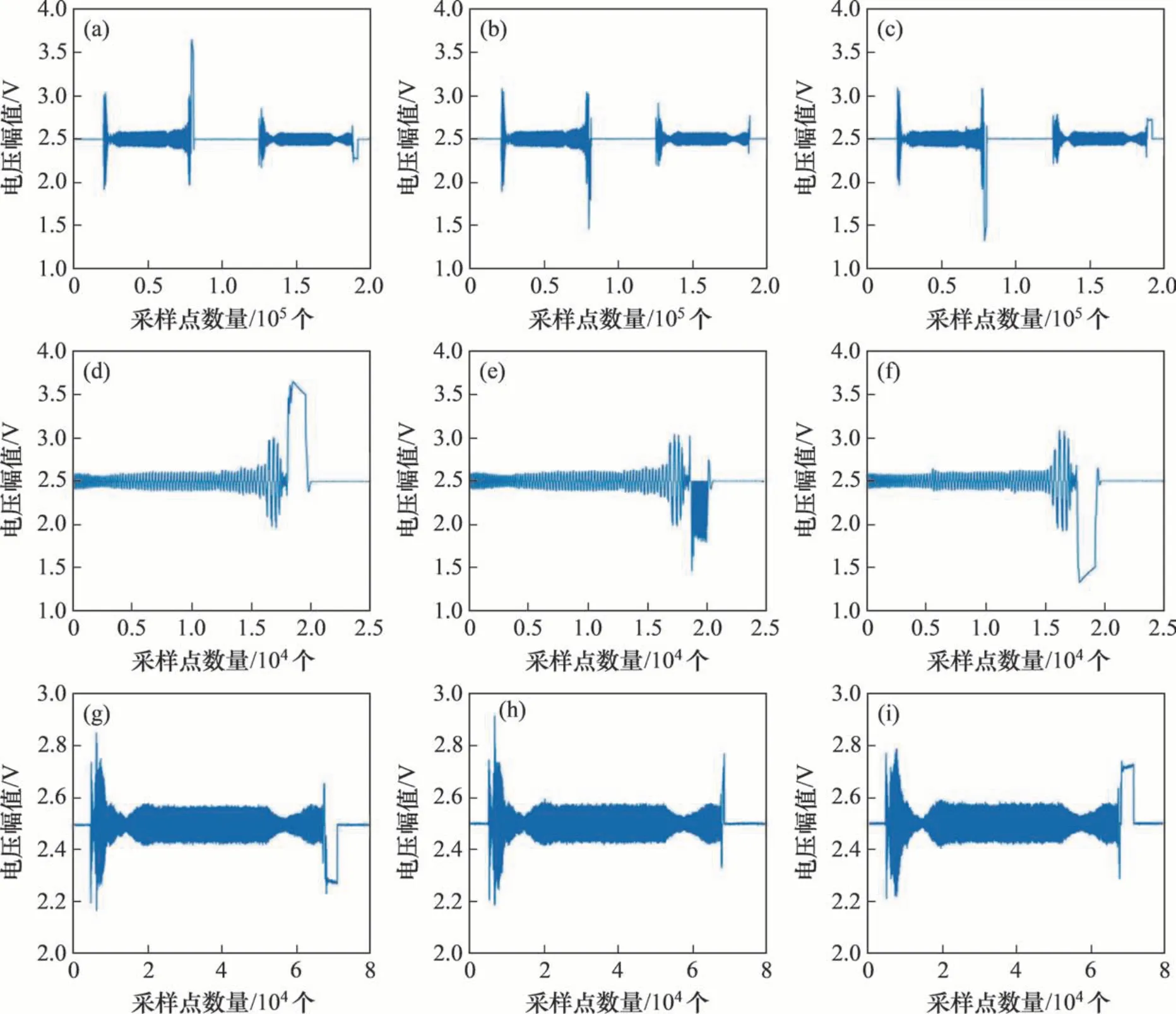
图8 地铁塞拉门不同状态数据波形图Fig.8 Data waveform diagram of different state of subway plug door

表3 地铁塞拉门不同状态数据实验结果对比Table 3 Comparison of experimental results of different state data for subway plug door

5 结论

1)将一维数据进行二维表示，经归一化形成灰度图进行压缩。降低了数据周期间的冗余，提高了压缩性能。

2)采用二维分块自适应阈值小波压缩算法，自适应分块，自动调整各块阈值。在压缩率一定的情况下，提高了数据重构精度。

3)以江苏某地铁车辆现场采集的地铁塞拉门开关门实测数据进行实验验证。实验证明该算法在幅值较小的区域可以保留更多的时频细节信息。

4)二维分块自适应阈值小波压缩算法效果稳定，对地铁塞拉门PHM 故障诊断具有一定的实用价值。