基于Gabor小波的汽车金属材料表面微小缺陷快速识别

2021-05-17周李洪龚金科李兵

中南大学学报（自然科学版） 2021年4期

周李洪，龚金科，李兵

(1.湖南大学机械与运载工程学院，湖南长沙，410082；2.湖南机电职业技术学院汽车工程学院，湖南长沙，410151；3.合肥工业大学电气与自动化工程学院，安徽合肥，30009)

在生产力水平迅速发展和工业技术、工艺水平不断提高的背景下，金属材料已广泛应用于社会发展的各个行业中，同时发挥了非常重要的作用。其中，汽车金属材料在加工时，会不可避免地出现一些缺陷，如铸造时生成的气孔、表层黏砂和夹砂等，还有锻造时的表层裂纹等。在材料整个使用周期中，在时间不断延长、气候和环境等一系列因素影响下，腐蚀和疲劳等不足也逐渐产生。此类缺陷会对材料整体使用寿命和力学特性等产生直接影响。一些微小缺陷的发展会造成材料失效同时出现断裂，因此，汽车金属材料表面微小缺陷的无损检测成为了急需解决的问题。国内无损检测起步相对较晚，但是整体发展很迅速。近年来，人们采用超声波、光声和机器视觉等多种手段进行了相应研究[1-2]。无损检测指的是以不破坏对象正常使用功能为前提条件，使用现代化技术与设备对因材料缺陷造成的异常进行检测，以此得到缺陷信息的检测技术，其能够减少及消除金属材料隐患。该技术为工业发展过程中不可或缺的有效工具，在提高生产力和促进国家发展中具有重要的现实意义[3-4]。李萍等[5]提出了一种基于深度学习的缺陷识别方法，通过卷积神经网络模型获得汽车金属材料表面缺陷特征，通过深度学习对汽车金属材料表面特征进行分析，提升了对汽车金属材料微小缺陷识别的适应性，但是缺陷类型判断效果不佳。兰红等[6]提出了三维灰度矩阵的汽车金属材料缺陷识别方法，通过图像灰度矩阵对样本图像空间特征进行分割，通过三维灰度矩阵构画等值线图，结合全局搜索与局部搜索方法确定材料表面凹凸区域位置，实现对微小裂纹缺陷精确定位。此方法能够有效提升缺陷识别率，但是抗干扰效果不佳。因此，为了有效地识别汽车金属材料表面缺陷，并进行及时处理，本文作者提出基于Gabor小波的汽车金属材料表面微小缺陷快速识别方法，利用Gabor小波技术对光照干扰进行处理，通过改进Otsu 阈值分割方法对汽车金属材料表面微小缺陷图像进行分割，然后，通过Gabor模板卷积操作获取图像边缘，实现汽车金属材料表面微小缺陷的快速识别。

1 基于Gabor 小波的汽车金属材料表面微小缺陷识别

1.1 汽车金属材料缺陷图像分割

为了提取图像中的缺陷，首先对图像进行分割，引入Otsu 阈值分割法对图像进行分割。该分割法可称作最大类间方差法，其运行原理为将原始图像基于灰度划分成目标与背景2个类别，同时使其类间的方差最大化。该算法的整个过程在图像一维直方图中执行。当获取图像一维直方图后，算法执行时与图像尺寸没有相关性，由此执行效率非常高。图1所示为汽车金属材料表面缺陷图。

假设图像中灰度i的像素占据整个图像的比例为pi，整幅图像灰度均值以t为阈值对缺陷图像C进行分类，分别为C0和C1，2个类别占据的比例为

图1 汽车金属材料表面缺陷图Fig.1 Surface defects of automotive metal materials

2个类别各自的灰度均值为传统Otsu算法目标函数是C0和C1这2个类别的类间方差，表示形式为

式中：ω0(t)为C0类缺陷图像类别占比；ω1(t)为C1类缺陷图像类别占比；μ0(t)为C0类缺陷图像灰度初始值；μ1(t)为C1类缺陷图像灰度初始值。

能够使式(3)获取最大值的t*就是分割阈值，从数学上证明式(3)最大化的目标函数Q(t)的表达式为

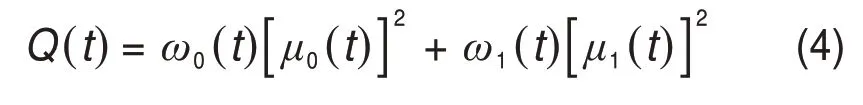
其中，最佳阈值t*可利用下式得到：

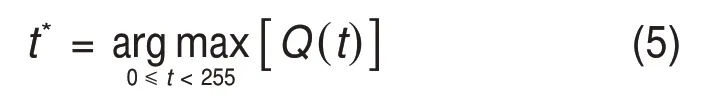
图2所示为缺陷图像的灰度直方图。从图2可以看出：直方图具有单峰性特征，不具备显著性双峰特征，使用Otsu 算法获得的阈值通常不在谷底部位，因此，传统Otsu 算法无法获取理想的图像分割结果。

图2 缺陷图像的灰度直方图Fig.2 Gray histogram of defect image

针对上述问题提出改进Otsu 算法，对图像进行分割。汽车金属材料表面微小缺陷属于小目标，因此，表面缺陷在图像中占据的比例非常低，导致图像直方图呈近单峰特征。根据分割阈值处在谷底的特征，通过强调谷底条件下的改进Otsu 算法实现图像分割。该算法与传统Otsu 算法最大的不同体现在目标函数上，改进算法目标函数Q(t)的表示形式为

由式(6)可知，该目标函数添加了权重参数(1-pt)。其中，pt越小，则表示出现概率越小，其在目标函数中占据的权重就越大，由此该目标函数能够确保阈值一直处在谷底，使占据图像比例相对大的背景可以被忽视，占据比例较小的缺陷目标可以被提取[7-8]。

综上可知，改进Otsu算法执行步骤如下。

步骤1：遍历图像中所有像素，统计图像一维灰度，并对各灰度出现概率进行计算。

步骤2：遍历所有灰度t，利用式(6)计算相应目标函数。

步骤3：在所有目标函数中寻找最大值，该最大值相应灰度t*就是分割阈值。

步骤4：将灰度比阈值低的像素灰度设置成0，剩下灰度设置为255，获取分割之后汽车金属材料表面图像的二值化图像。

1.2 缺陷识别

对上述缺陷图像进行分割后，将Gabor小波与马氏距离法结合，可快速识别汽车金属材料表面微小缺陷。

1.2.1 Gabor小波变换

Gabor 滤波器(带通滤波器)具有频率选择与方向选择等特征。因Gabor小波变换窗口函数为1个固定值，假设将小波函数用在变换过程中，能够以高分辨率分析频域与时间域[9-10]。图像的边缘特征为畸变像素点构成的集合，Gabor小波函数能够捕捉到对应空间部位、频率及方向选择性的像素数据对缺陷边缘进行识别。利用Gabor小波实现缺陷识别，不仅可以去除噪声，而且可以很好地保留缺陷纹理特征。

利用直接由频域构建Gabor小波二维的卷积模板，提取相同尺度下的8个方向上特征图像实现二维边缘图像重构[11]。

假设在笛卡尔坐标系中，方向和尺度分别为u和v的二维Gabor小波函数gu(z) 表示形式为

式中：z=(x,y)，代表图像的像素点坐标；‖·‖代表相应值欧式范数[12]；σ为图像像素点的散布函数；ku,v为高斯窗口波长变化函数，它能够控制高斯窗口整体宽度、振荡部分波长和方向。

式中：kv为滤波器采样频率；kmax为最大的采样频率；f为频域范围内核函数间隔因子[13]；φu=πu/8，u为图像灰度函数，该值反映了滤波器整体方向选择性。

根据式(7)可知，Gabor 小波函数gu(z)为R′2→C′上的一个复值函数[14]，R′2为缺陷图像像素离散域，C′为缺陷图像类间方差集合，利用实部R′u(z)、虚部I′u(z)有

式中：I′u(z)为利用Gabor小波函数和图像g之间卷积所得虚部函数。设定图像中1 点g0(x,y)，利用Gabor小波描述g0(x,y)位置周边图像特征，则缺陷图像卷积函数G′u,v(g0) 可表示为

其中：*代表卷积操作；G′u(g0)为点g0(x,y)位置汽车金属材料表面微小缺陷图像卷积。在图像边缘定义中，G′u(g0) 为图像周边像素灰度的阶跃变化，或者是屋顶状变化像素构建的集合，图像边缘点为一种信号突变点或者奇异点[15-16]，因此，能够利用下式描述图像Gabor特征集合S′，即

根据上述Gabor小波特性，该集合S′能够捕捉图像不同频率和方向下边缘，还有局部明显特征，此类突变或奇异点构成的组合就是目标缺陷区域。

1.2.2 马氏距离法

马氏距离法能够描述数据协方差距离，为得到2个未知样本集合相似程度的可靠方法。因汽车金属材料微小缺陷存在的特征，传统欧式距离法仅对图像中2 点间距离进行计算，结果误差较大，容易受外界干扰[17]。当协方差矩阵为C′z时，缺陷图像中随机2 点x和y的马氏距离函数服从正态分布。针对根据n′个样本zi=(xi,yi)τ构建的样本空间z={(xi,yi)τ,…,(xn,yn)τ}，τ为样本在空间的分布密度，随机样本点和样本均值μ′z=(μ′x,μ′y)之间马氏距离Di,j的计算式为

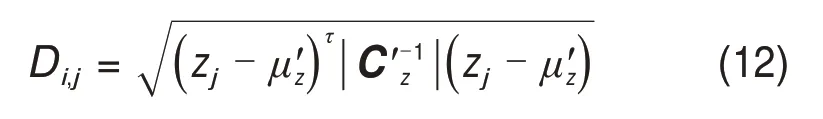
其中：

利用马氏距离能够增强图像边缘像素点的基本特征，并使缺陷兴趣区域像素点变得更为显著。传统马氏距离只是对整个图像协方差矩阵进行计算，对于兴趣区域、背景图像不进行划分，并且夸大了变化比较微小的像素，导致误检率较高[18]。经综合考虑，采用加权马氏距离实现图像增强处理。

在样本空间范围内，p′为特征维数，则当原灰度样本点和样本均值μ′=(μ′x,μ′y)时，将相关参数代入式(12)，获得马氏距离计算公式：

式中：Cij为灰度矩阵。

如果C′为正定阵，那么存在C′-1/2使式(16)成立：

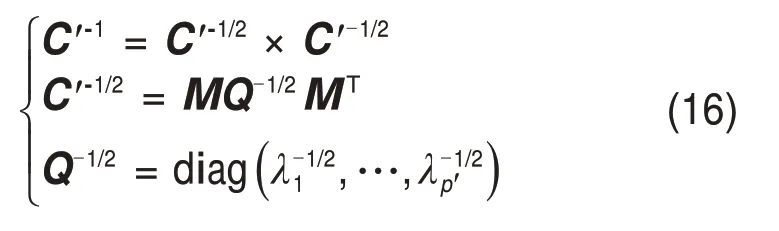
式中：λ1,…,λp′为C′的特征值；M列向量是对应单位特征向量；Q为缺陷图像边缘像素特征向量。综上，p′维空间范围内的点xi(p′)与样本均值μ′j(p′)之间加权马氏距离表达式为

加权之后图像中不同像素点权重见图3。

图3 加权后图像中不同像素点权重Fig.3 Weighting values of different pixels in weighted image

分析图3可知：归一化灰度与权重具有相关性，当归一化灰度为0.2时，权重为1.5，当归一化灰度为0.6时，权重为3.0；归一化灰度越大，权重增加越缓慢。

1.2.3 缺陷识别

在缺陷识别过程中，先对图像实行预处理，其中包含图像均衡化以及同态滤波等，以此去除光照产生的影响。利用模拟测试法得到Gabor滤波器运行中的最佳参数，对样本汽车金属材料表面微小缺陷图像进行Gabor模板卷积操作，获取边缘图像。针对边缘图像进行加权马氏距离计算，增强边缘轮廓特征。最后通过连通区域标记，检索并同时标记汽车金属材料表面的缺陷，实现缺陷识别。

综合Gabor滤波器自身组成特性，选择运行参数时，一般考虑的是频域空间[19-20]。在此，利用模拟试验机法，从整体到局部，设定在其他参数均为最优的前提下，剖析单个因素对图像边缘纹理产生的影响。其中，对Gabor函数提取图像边缘产生影响的主要参数包含卷积模板尺寸、最大的采样频率和空间频率以及滤波器模板大小等。

在Gabor 卷积模板尺寸选择中，当模板由16像素*16像素顺次增加到128像素*128像素时，对应的滤波器形状也会发生变化。在Gabor卷积模板范围不断增加下，对应Gabor卷积核非零部分变得越来越小，表示其提取到的特征不断趋向细节特征。由此，要基于具体应用选取合适Gabor 核函数窗。

假设最大样本采集频率为π，那么得到的边缘纹理非常细腻，特征十分显著，但是容易受到噪声影响；假设空间频率为π，那么得到的边缘纹理相对模糊，且细节特征显著性不强。因此，实验确定最大样本采集频率为π/2，而空间频率取为π/3。

当滤波器尺度(滤波算子的空间作用范围，对于高斯类算子指其均方差)相对小，则提取到的特征比较细腻，但受噪声影响。在尺度不断增加下，边缘细节会逐渐丢失，还会产生偏移现象。除此之外，多尺度会大大增加整体计算量。

加权马氏距离在阈值化之后，得到的边缘存在细微毛刺，利用设定阈值将毛刺去除会出现误检毛刺。经模拟可知，若阈值过小则会导致得到的边缘较粗糙，增加了误检率。若阈值过大，则导致边缘过于细腻，漏检率会偏高，并且容易受噪声影响。经测试，最佳阈值约为0.6。

在缺陷图像分割基础上，进行如下步骤。

步骤1：输入带有缺陷并分割完成的图像，对图像进行进一步处理。

步骤2：构建二维Gabor 小波函数。在指定尺度和不同方向下，构建8个方向上的Gabor卷积模板，并针对各方向下模板和缺陷图像进行Gabor卷积操作，得到8个卷积图像，然后利用逆滤波实现图像复原，获取Gabor提取到的边缘图像。

步骤3：利用步骤2 得到汽车金属材料表面微小缺陷边缘图像，对总灰度均值μ′=(μ′x,μ′y)进行计算。得到图像各像素点灰度zi=(xi,yi)τ，并构建权重函数。对加权像素数据集合进行计算，对协方差矩阵进行重新估计。

步骤4：基于加权马氏距离计算式获取任意灰度样本和总样本之间差值，以增强图像边缘特征。

步骤5：利用连通区域标记法实现兴趣区域检索和标注。引入2次扫描法，在第一次扫描时赋予不同label 值，二次扫描时对相邻连通区域label 值进行同化。最后在原图像中标记缺陷具体位置。图4所示为缺陷识别流程示意图。

2 实验结果与分析

在验证基于Gabor小波的汽车金属材料表面微小缺陷快速识别方法有效性过程中，将实验平台搭建在Matlab 上，对汽车空调压缩机表面缺陷进行实验检测，以验证所提技术实用性。压缩机缸体由灰铁(N0.35)铸造而成，其长×宽×高为370 mm×230 mm×180 mm。实验数据来源于某汽车生产厂家，共采集了横向划伤、纵向划伤和网纹等几种缺陷图像数据，原始图像像素为732×287。为了实验方便，在原始图像中截取128×128 带有缺陷的区域，共得样本为1 356 个，其中1 个样本中可能含有多种类型缺陷。

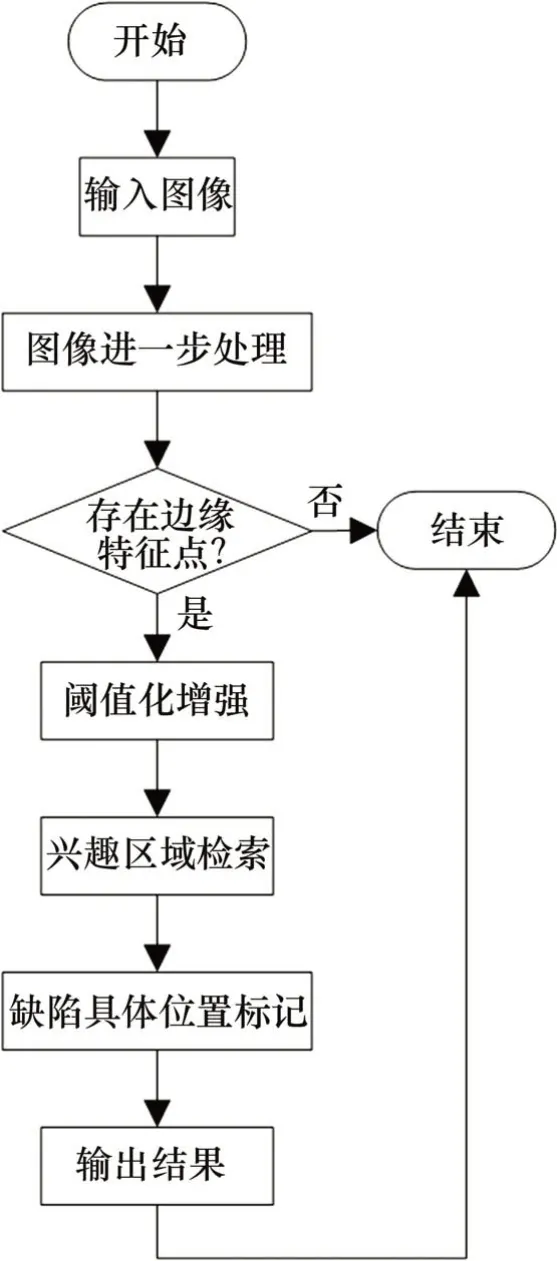
图4 缺陷识别流程示意图Fig.4 Schematic diagram of defect identification

2.1 缺陷识别结果

为了验证缺陷识别效果，采用三维灰度矩阵法、深度学习法以及Gabor小波法对汽车金属材料缺陷进行识别，得到放大10 000 倍后的电镜识别结果如图5所示。

图5 不同方法的缺陷识别效果Fig.5 Defect recognition effect of different methods

由图5可知：采用不同方法所得检索效果不同。采用三维灰度矩阵法识别出的缺陷图像清晰度明显较低，只能在检测结果中看见较为明显的3个缺陷，但是缺陷是凹陷还是凸起无法确定，缺陷识别效果不佳；采用深度学习法识别出的缺陷图像比较模糊，可能是受到了噪声的影响，缺陷识别效果较差。而图5(c)中的缺陷识别图像结果清晰度较高，能够有效确定缺陷位置，同时可以区分缺陷类型，说明Gabor 小波法具有较好的识别效果。

2.2 缺陷识别正确率对比

利用不同方法对比结果验证所提方法正确性，所得结果见图6。

图6 缺陷识别正确率Fig.6 Defect recognition accuracy

由图6(a)可知：采用不同方法所得横向划伤识别率不同；当样本图像数量为100幅时，三维灰度矩阵法的横向划伤识别率为87%，Gabor小波法的横向划伤识别率为99.5%，深度学习法的横向划伤识别率为83%；当样本图像数量增加到900 幅时，三维灰度矩阵法的横向划伤识别率为89%，Gabor小波法的横向划伤识别率为98%，深度学习法的横向划伤识别率为77%。采用本文方法所得横向划伤识别率一直较高。

由图6(b)可知：不同方法的纵向划伤识别率不同；当样本图像数量为300幅时，三维灰度矩阵法的纵向划伤识别率为79%，Gabor小波法的纵向划伤识别率为94.9%，深度学习法的纵向划伤识别率为77%；当样本图像数量增加到900幅时，三维灰度矩阵法的纵向划伤识别率为78%，Gabor小波法的纵向划伤识别率为95%，深度学习法的纵向划伤识别率为80%。本文方法的纵向划伤识别率较高。

由图6(b)～(f)可知：本文方法的横向裂纹识别率、纵向裂纹识别率、网纹识别率以及压痕识别率比其他2种传统方法的高，说明这种方法很好地解决了由于微小变化导致的误检问题，增强了汽车金属材料表面微小缺陷边缘特征，提高了缺陷识别率。

在上述基础上检测不同方法对金属缺陷的误判率，结果如表1所示。

表1 不同方法的缺陷误判率Table 1 Defect misjudgment rates by different methods

由表1可知：当识别出的缺陷图像数量为100幅时，三维灰度矩阵法的缺陷误判率为32%，深度学习法的缺陷误判率为22%，Gabor小波法的缺陷误判率为1%；在700 幅缺陷图像中，三维灰度矩阵法的平均缺陷误判率为32%，深度学习法的平均缺陷误判率为22%，Gabor小波法的平均缺陷误判率为1%。采用本文方法所得缺陷误判率比其他2种方法的低，缺陷识别效果好。

2.3 缺陷识别用时对比

采用sigmaplot 软件获得上述3 种方法的缺陷识别用时，结果如图7所示。

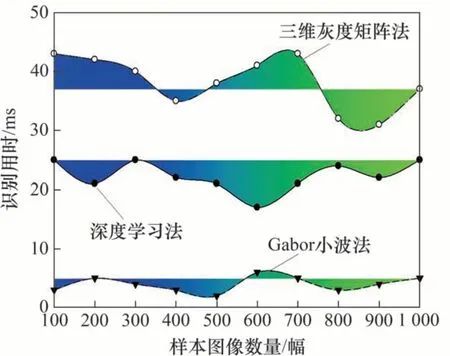
图7 缺陷识别用时Fig.7 Defect identification time

由图7可知：当样本图像数量为200幅时，三维灰度矩阵法的缺陷识别用时为42 ms，深度学习法的缺陷识别用时为21 ms，Gabor 小波法的缺陷识别用时为5 ms；当样本图像数量为800幅时，三维灰度矩阵法的缺陷识别用时为32 ms，深度学习法的缺陷识别用时为24 ms，Gabor 小波法的缺陷识别用时为3 ms。本文方法的缺陷识别用时始终较短，说明本文方法的识别效率最高，实现了汽车金属材料表面微小缺陷快速识别。