网格划分对多级离心泵水力性能计算精度的影响

2021-05-17刘志远王秀勇杜永峰汪东山

西华大学学报（自然科学版） 2021年3期

刘志远，王秀勇，杜永峰，汪东山，吕雪

（兰州理工大学能源与动力工程学院，甘肃兰州 730050）

近年来，CFD 技术在泵的性能预测、流场分析和水力优化方面被广泛应用，并取得了良好的效果[1 − 7]，同时在提高泵水力性能方面发挥了较大的作用。目前，提高CFD 的计算精度依然是研究的重点内容，其影响因素众多，其中一个重要因素就是计算域的网格划分。

网格划分是进行CFD 计算的关键一步，是保障数值计算精度的重要一环[8 − 9]。文献[10]探究了不同计算网格对离心泵数值计算精度的影响，结果表明计算网格中含有近壁面网格时计算精度最高，流场结构更符合实际流动情况。文献[11]以核主泵为研究对象，基于六面体网格，探究了影响核主泵计算精度的因素，结果表明合理的近壁面网格尺度能有效提高水力性能的计算精度。从目前已有研究来看，多级离心泵的研究主要集中在对泵内部流场的优化与分析中[12 − 15]，而关于多级离心泵计算精度的研究还比较少，尤其是关于网格划分对多级离心泵计算精度影响的研究更少，因此有必要研究不同网格划分对多级离心泵水力性能计算精度的影响。

本文以节段式多级离心泵为研究对象，采用ICEM 软件将计算域分别划分为四面体网格、混合网格和六面体网格3 种网格方案，在网格无关性的基础上，采用FLUENT 软件在多流量工况点进行数值计算，并对各网格划分方案的计算精度进行综合分析，以期在网格划分方面为提高多级离心泵的水力性能计算精度提供参考。

1 计算模型与网格划分

1.1 计算模型

计算模型为13 级节段式离心泵，其设计参数为：流量Qd=90 m3/h，扬程H=1 500 m，转速n=2 980 r/min，首级叶轮的叶片数为5 枚，次级为6 枚，正导叶和反导叶的叶片数均为9 枚。计算域主要包括吸水室、首级叶轮、次级叶轮、导叶、压水室、叶轮前后腔体及各级口环间隙。

1.2 网格划分

为了研究计算域网格划分的不同对多级离心泵水力性能计算精度的影响，分别采用3 种网格划分方案来进行定性分析。一是全计算域均采用四面体网格，其中导叶、压水室和吸水室的网格尺度为4 mm，叶轮的全局网格尺度为2 mm，叶片表面网格尺度为1 mm，网格总数为3 740×104；二是采用混合网格，即核心过流部件叶轮采用六面体网格，其第一层网格高度为0.4 mm，网格增长比率为1.2，其余各过流部件采用四面体网格，网格尺度与方案一相同，网格总数为3 078×104；三是全计算域均采用六面体网格，各过流部件近壁面第一层网格的高度均为0.4 mm，网格增长比率为1.2，网格总数为2 408×104。各方案的网格划分情况如图1 所示。经网格无关性计算验证，上述各方案的网格数量均满足要求。

图1 多级泵网格划分

图2 所示为四面体网格和六面体网格无量纲壁面距离y+的分布情况。其中四面体网格y+值的分布区间较宽，集中度不高，主要分布在500～900 区间范围内；六面体网格y+值分布较为集中，主要集中在0～300 的区间范围内。很显然，采用六面体网格划分方案时，由于在近壁面处对网格进行加密处理较为方便，能够明显降低全计算域的y+值，可以更好地满足湍流模型对近壁面网格尺度的要求。

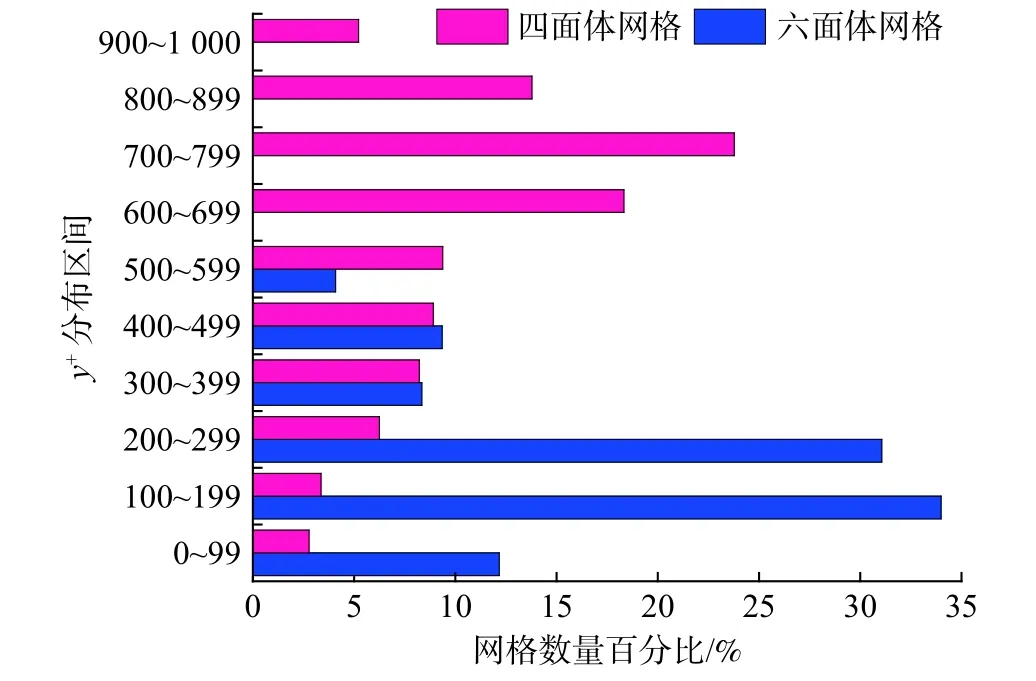
图2 近壁面y+的分布情况

2 数值计算方法与求解设置

湍流模型选择工程中常用的RNGκ-ε模型和标准壁面函数组合，压力与速度的耦合采用SIMPLEC 算法。计算域中静止和旋转过流区域之间采用多重参考系模型，各个过流部件之间通过Interface 边界条件进行数据传递。泵的进出口分别设定为速度入口和自由出流边界条件，壁面设置为无滑移壁面条件。当泵出口处的静压变化趋于稳定时即认为计算收敛。

3 计算结果分析

3.1 不同网格的水力性能计算结果对比分析

图3 所示为不同网格划分方案在多工况条件下对多级离心泵扬程的计算结果。从扬程计算曲线和试验曲线在多工况范围内的对比来看，各网格方案基本能够计算出扬程随流量增加时的变化趋势，均能够反映出1.0Qd工况点之前扬程下降较慢，1.0Qd工况点之后扬程下降较快的曲线特征。由3 种网格方案扬程的计算值和试验值之间的比较来看，六面体网格扬程的计算值在0.5Qd工况点明显高于试验值，在0.72Qd工况点与试验值相当，在其余工况点则均低于试验值；而四面体网格与混合网格扬程的计算值在（0.5～1.5）Qd流量工况区间内均明显高于试验值，随着流量的增大，混合网格扬程的计算值与试验值之间的偏差呈现先减小后增大的趋势，而四面体网格的偏差则持续增大。由各网格划分方案扬程计算曲线的对比来看，混合网格和六面体网格的计算曲线除在0.72Qd工况点之前比四面体网格的偏高且明显偏离试验曲线外，在其余工况点均偏低且更接近试验曲线；在（0.5～0.9）Qd工况区间内，随着流量的增大，四面体网格扬程计算曲线的变化趋势与试验曲线吻合度较好，而混合网格和六面体网格扬程计算曲线的下降速度较快；在0.9Qd工况点之后，六面体网格扬程计算曲线随流量增大时的变化趋势与试验曲线几乎一致，混合网格和四面体网格扬程计算曲线的下降速度相对较慢，其中四面体网格扬程计算曲线与试验曲线之间的差异最大。从多工况点综合来看，六面体网格的扬程计算曲线与试验曲线之间的吻合度最高，其次是混合网格，而四面体网格扬程计算曲线与试验曲线之间的吻合度相对较低。

图3 不同网格的扬程计算结果

从扬程相对计算误差的角度来看，随着流量的增加，3 种方案相对计算误差变化趋势各不相同。在多流量工况条件下，四面体网格方案相对计算误差变化呈现逐渐增大的趋势，最大误差值出现在1.5Qd工况点，为5.31%，其余工况点计算误差均在3.67%以内；混合网格方案相对计算误差在0.9Qd工况点之前呈现单调下降的趋势，在0.9Qd工况点之后随着流量增加逐渐增加，最大误差同样出现在1.5Qd工况点，为3.41%；而六面体网格方案在多流量工况下，相对计算误差变化趋势不稳定，但整体计算误差不大，相对计算误差最大值出现在0.5Qd工况点处，为1.90%，其他工况点相对计算误差位于0.10%～1.44%之间。

总体来看，在多工况条件下，六面体网格方案扬程计算曲线与试验曲线之间的吻合度远高于其他两种网格方案，在扬程性能预测中具有一定的优势。

图4 所示为在多工况条件下不同网格划分方案的轴功率计算结果。从3 种网格划分方案轴功率的计算值和试验值之间的对比来看，各方案的计算值除了在0.5Qd工况点略高于试验值外，在其他工况点均低于试验值；混合网格和六面体网格的轴功率计算值与试验值之间的吻合度要明显高于四面体网格，其中混合网格的计算值除了在0.5Qd工况点略高于六面体网格外，在其余工况点均偏低；六面体网格的轴功率计算值在各个工况点与试验值之间的吻合度最高。从轴功率的计算曲线和试验曲线在多工况条件下的总体对比来看，各网格方案均能够计算出轴功率随流量增加时的变化趋势，有所不同的是，随着流量的增加，四面体网格和混合网格轴功率计算曲线的斜率增长速度在1.0Qd工况点之前明显慢于试验曲线，而在1.0Qd工况点之后则快于试验曲线，导致四面体网格和混合网格的轴功率计算曲线与试验曲线之间有较大的偏差，其中四面体网格的偏差最大；六面体网格的轴功率计算曲线随流量增加时的变化趋势与试验曲线之间具有良好的吻合度，其吻合度是3 种网格划分方案中最高的。

图4 不同网格的轴功率计算结果

由各网格划分方案对轴功率相对计算误差的大小来分析，四面体网格除了在0.5Qd工况点轴功率相对计算误差比较小外，其余工况点的相对计算误差均明显较大，远超过其他两种方案，其最大误差出现在1.2Qd工况点，为9.12%，随着流量的进一步增加，相对计算误差又呈现递减的趋势；混合网格与六面体网格相对计算误差的变化趋势基本类似，均在1.2Qd工况点出现最大计算误差，分别为5.05%和2.44%，最小相对误差均在1.5Qd工况点，分别为0.87%和0.22%；六面体网格在各个工况点的轴功率相对计算误差均明显小于其他两种网格划分方案，其计算精度是最高的。

总体来看，在进行多级泵的轴功率性能预测时，六面体网格方案具有较高的计算精度，不论是在轴功率的相对计算误差上还是计算曲线与试验曲线的吻合度上均具有一定的优势。

图5 所示为不同网格划分方案在多工况条件下对多级离心泵效率的计算结果。从各方案效率的计算值和试验值之间的对比来看，除了在0.5Qd工况点各网格的计算值与试验值非常接近外，在其他工况点都高于试验值，其中四面体网格的效率计算值在0.5Qd工况点之后明显高于混合网格和六面体网格，并且该偏差值随着流量的增加逐渐加大；而混合网格效率的计算值虽比四面体网格小，但也同样明显大于六面体网格；六面体网格效率的计算值在各个工况点只是略微大于试验值。从效率计算曲线和试验曲线在多工况条件下的对比来看，六面体网格的计算曲线和试验曲线之间的吻合度较高，能够较为准确地反映出效率在（0.5～1.0）Qd工况区间内快速提升、在（1.0～1.4）Qd工况区间内增速放缓并且在1.4Qd工况点附近达到最高值之后又缓慢下降的变化趋势；混合网格的效率计算曲线也基本能够反映出效率随流量增加时的变化趋势，但在1.0Qd工况点之前计算曲线的斜率大于试验曲线，其计算精度不如六面体网格；而四面体网格的效率计算曲线随流量增加时的变化趋势和试验曲线之间存在较大差异，在1.2Qd工况点之前计算曲线的斜率明显大于试验曲线，在（1.2～1.5）Qd工况区间内则比较平坦，反映出的高效区宽于试验曲线，计算精度较低。

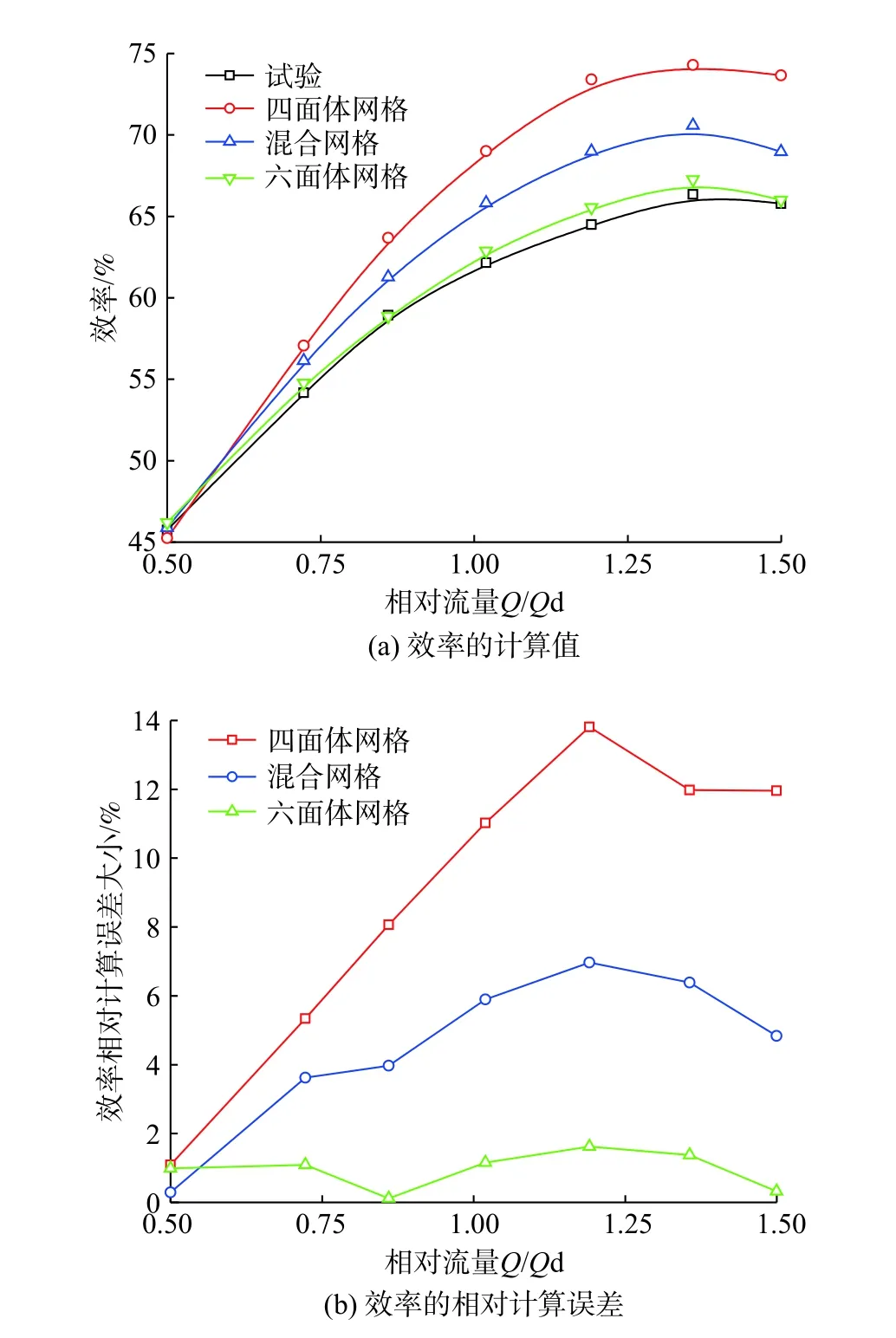
图5 不同网格的效率计算结果

从各网格划分方案的效率相对计算误差大小来分析，四面体网格的计算误差除了在0.5Qd工况点相对比较小外，在其余工况点均较大，且明显高于其他两种方案，最大误差出现在1.2Qd工况处，为13.81%，之后相对误差随着流量进一步的增加而逐渐减小；混合网格的计算误差在（0.5～1.2）Qd工况内呈现单调递增的变化趋势，在1.2Qd工况点处出现最大相对计算误差，为6.97%，随着流量的进一步增加相对计算误差再次递减；六面体网格相对计算误差的最大值在1.2Qd工况点，为1.62%，其余工况点的相对计算误差均未超过1.4%，在多工况条件下表现出了较高的计算精度。

总体来看，在对多级离心泵的效率进行性能预测时，六面体网格方案具有较高的计算精度，能够获得较为准确的效率计算曲线。

综上所述，对多级离心泵进行性能计算时，全局采用六面体网格并在近壁区域对局部网格进行加密处理的网格划分方法，其计算精度最高；其次是混合网格，也就是旋转部件采用六面体网格、静止部件采用四面体网格的网格划分方法，能够获得相对较高的计算精度；而全局为四面体网格的网格划分方法，计算精度最低。对过流部件合理的网格划分是保障计算精度的关键。

3.2 不同网格的计算误差综合分析

计算精度是判断各方案优劣的重要标准之一。在多工况条件下，将单一工况点计算结果连接成线，此时计算精度的高低就体现为计算曲线和试验曲线的吻合度上。而相对计算误差大小的平均值和相对计算误差的均方差是影响吻合度的主要因素。相对计算误差的平均值反映的是计算值和试验值之间的偏差大小，而均方差反映的则是计算曲线与试验曲线在曲线形状上的相似程度。当平均值和均方差都较小时，此时性能计算曲线与试验曲线之间的吻合度较高，表明计算精度也较高。

表1 所示为在多工况条件下3 种网格划分方案相对计算误差的综合统计结果。从表1 可知，在多工况条件下，四面体网格对各性能参数的计算误差最大，计算曲线与试验曲线之间的吻合度也最低；而将叶轮划分为六面体网格并对近壁面区域的网格进行加密处理后，上述两个问题得到了明显的改善，尤其是效率相对计算误差的平均值减小了4 个多百分点，相对计算误差的均方差也减小了2 个多百分点；当将计算域全局划分为六面体网格并对近壁区域的网格进行加密处理后，各性能参数相对计算误差的平均值和均方差进一步减小，均未超过1.29%和0.99%。由此可知，在数值计算方法不变的前提下，网格划分方案能否准确解析近壁面区域低雷诺数的流动特征是提高数值计算精度的关键。

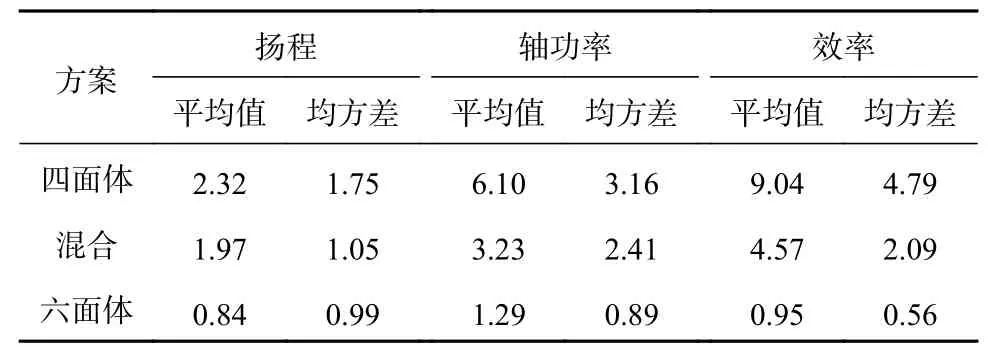
表1 多工况点计算误差分析 %

在工程应用过程中，设计工况点通常是泵类产品正常运行的工况点，对泵进行水力优化时，通常也是根据设计工况点的参数要求进行水力设计和数值分析，所以有必要单独在设计工况点对3 种网格划分方案的计算精度进行分析比较。表2 所示为在设计工况点3 种网格划分方案计算误差的统计结果。从表2 可知，在设计工况点，六面体网格划分方案不论是在扬程、轴功率和效率等单个性能参数的计算误差大小方面，还是在3 个性能参数综合计算误差的平均值和均方差方面，最大值均未超过1.2%，其中扬程相对计算误差的大小仅为0.71%，各方面均表现出了很高的计算精度；混合网格方案关于3 个性能参数计算误差的平均值和均方差分别比六面体网格高出了2.72 和3.19 个百分点，而四面体网格方案则比六面体网格分别高出了5.81 和6.72 个百分点。可见，在设计工况点对多级离心泵进行水力性能计算时，采用六面体网格划分方案更加合理，可以获得较高且相对可靠的计算精度，从而为提高产品性能、缩短设计周期、节约加工制造成本奠定良好的基础。

表2 设计工况点计算误差分析 %

综上所述，从网格划分难易程度、网格数量、近壁区域网格尺度和多级离心泵水力性能的计算精度等方面进行综合分析可知，对全流场进行四面体网格划分的难度最小，但网格数量较多，尤其是对近壁面区域的四面体网格进行加密后网格数量更多，即使如此其计算精度仍然是最低的，可见使用四面体网格对近壁面区域加密后并没有起到提高计算精度的作用，加密后庞大的网格数量反而过度占用了计算机资源；混合网格划分方案虽然在网格划分难易程度上较四面体网格偏难，但可以有效控制叶轮的网格数量和近壁面网格无量纲距离y+的值，同时其计算精度比四面体网格明显提高；全流场采用六面体网格划分方案，从网格划分的难易程度和时间耗费来看，六面体网格划分难度最大，耗费时间多，但可以合理控制全流场近壁面区域网格尺度y+值的分布，有效地反映了壁面对流动核心区的影响，使各项性能参数的计算精度明显高于其他两种网格划分方案，同时采用六面体网格后还可以减少全流场的网格数量，节约计算时间。在多级离心泵水力性能计算过程中，全流场网格划分方案采用六面体网格，能有效地保障数值计算的精度，提高理论指导实践的可靠性。