某静态混合器内气液两相流动及压降特性数值模拟
2021-05-17张慧宇张惟斌韩宇明衡亚光江启峰博华
张慧宇,张惟斌,2,韩宇明,衡亚光,2,江启峰,2*,G·博华,2
(1. 西华大学能源与动力工程学院,四川 成都 610039;2. 西华大学流体及动力机械教育部重点实验室,四川 成都 610039)
孔盘式静态混合器是一种新型高效的混合设备,被广泛地运用于多相流的混合、反应、分散、传质和传热,在核能、化学、原子能、航天、医药等领域广泛存在。通过各层塞孔强化相间相互作用[1],实现气液相混合,结构简单、安装方便、无液泛,对于相际传质的气液两相体系的混合操作具有良好的应用前景。但是,由于气液两相流流动过程中的不确定性,以及两相间界面效应的存在[2],且相界面的状态、形状和相介质的分布不但随空间、时间的变化而变化,还随含气率、管道几何尺寸和管道的空间内置元件等因素而改变,同时相间还出现不可忽略的滑移速度,致使流动特性变得更加复杂。
在评价静态气液混合器时,压降是决定传质传热效果的主要参数之一,通过观测压降的大小可以判断出能耗的高低[3]。目前,对于气液混合器流体动力学研究主要集中于SK、SMV 和SMX 型[4 − 9],其中的气液流动模式和接触方式与堆叠孔盘有较大区别,而针对孔盘式的气液混合流动含气率对压降的影响研究较少。与孔盘相关的研究主要集中于气液两相流通过管道内孔板的阻力系数与孔板参数的问题。余冬梅等[10]研究了多孔孔板水力空化装置的阻力特性,发现不同孔板的阻力系数与该孔板的结构参数有很大的关系。白兆亮[11]针对有压输水管相邻孔板间距局部阻力进行了试验,并用相邻影响系数对传统计算公式进行了修正。卢晓江[12]试验研究了不同开孔率的多孔孔板水力空化,结果显示单个多孔孔板阻力系数随着流量的增加,有增长的趋势但变化幅度不大,随着开孔率的增加,管路的阻力系数明显减小。
本文从设计应用出发,在涵盖工程实际应用的气液流量范围内,运用流体力学计算软件CFX 对孔盘式静态混合器内不同气液比下气液两相流的压力场进行数值模拟计算,分析了不同雷诺数对孔盘式静态混合压降的影响,旨在为工程应用中孔盘式静态混合器的设计提供参考。
1 孔盘式静态混合器计算模型简介
1.1 静态混合器计算区域及参数设置
本文研究的某孔盘式静态混合器主要由器顶封头、孔盘组、整流元件以及器釜组成。其中孔盘组由5 块直径为500 mm、高5 mm 的不锈钢孔盘等间距堆叠组成的圆形蜂窝结构,盘间由直径为10 mm、圆心间距为15 mm 的交错式通孔组成。器釜上部分别设有气体进口(40 mm)和液体进口(100 mm),下部设气液混合出口。气液混合按一定的比例依次通过以上4 个元件,经各相混合后,流体从器釜底部出口排出。混合器结构如图1所示。
选择4 种不同的网格单元数进行网格无关性验证,每种网格均采用非结构网格来离散计算域并对孔盘进行加密处理,如图2 所示,4 种不同的网格单元数如表1 所示。由于主要研究孔盘式静态混合器内气液两相流含气率对压降的影响,因此通过4 个算例中混合器进出口压差对比,来确定适合的网格单元数。计算结果表明当网格单元数由6 761602 增加到7266908,进出口压差的相对变化率为3.3%,此时认为计算结果与网格数量无关。考虑到时间成本和计算机资源,本文采用计算域网格单元数为6761602。
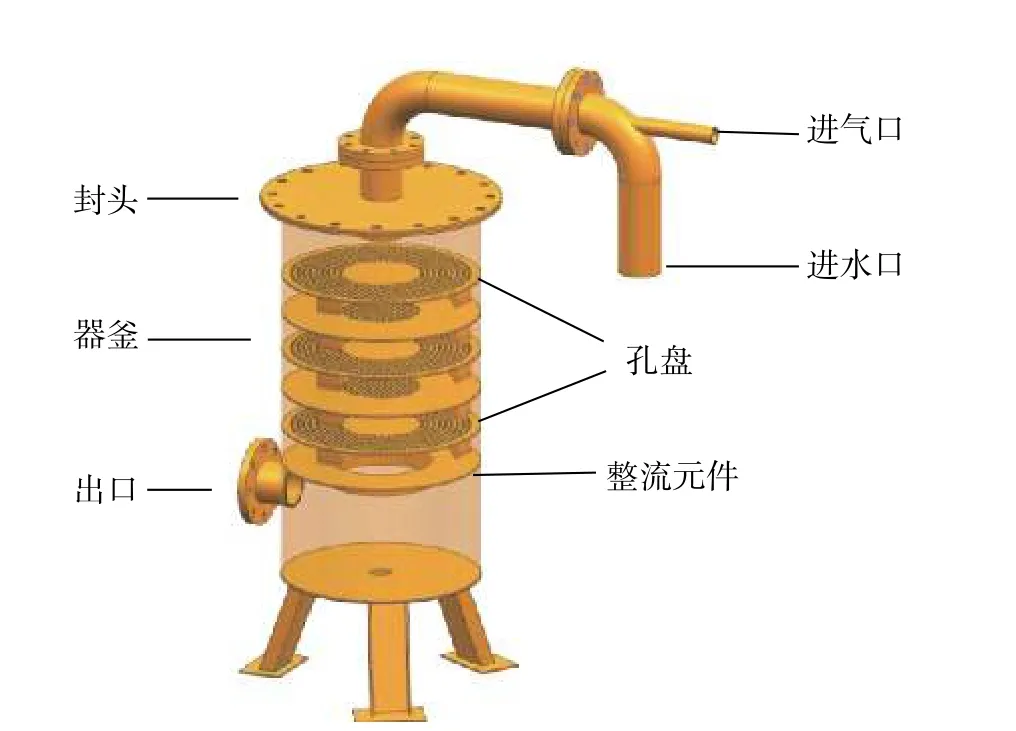
图 1 混合器结构示意图
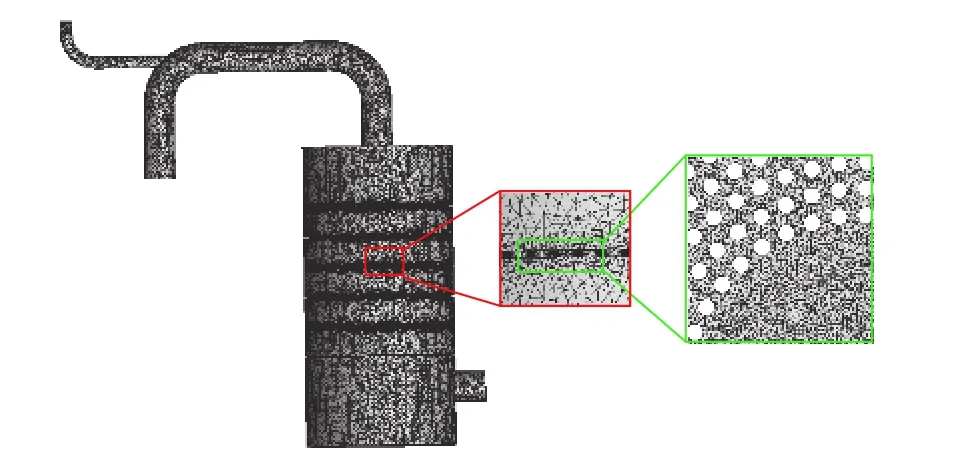
图 2 计算域三维水体网格模型
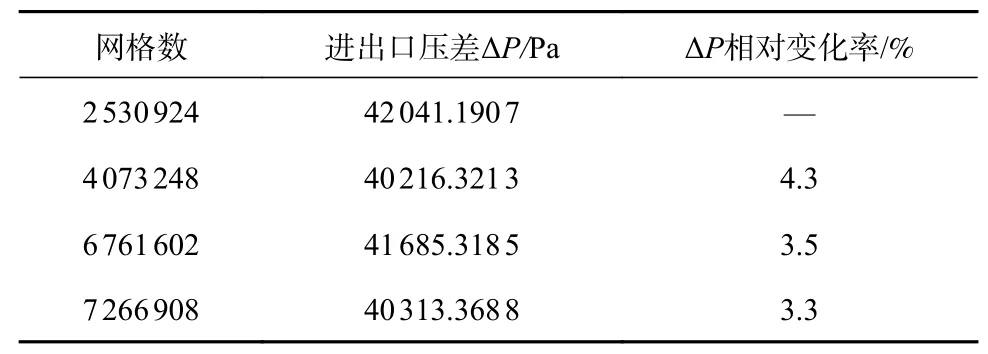
表 1 网格无关性验证
计算域内边界条件设置如下:相对压强为1atm,介质为水和空气(25℃)。气相和液相进口均采用速度入口且流动方向均垂直于进口边界,计算工况如表2 所示。出口边界条件为−10 Pa,方向垂直于出口边界。壁面采用无滑移边界条件。

表 2 混合器计算工况参数
1.2 数学模型
数值计算采用基于SST(Shear Stress Transport)模型的k-ω方程。该模型考虑了湍流剪切应力的传输,可以精确预测流动的开始和负压梯度条件下流体的分离量。SST 模型最大的优点在于考虑了湍流剪切应力,从而不会对不同气液比下涡流黏度造成过度预测。
湍动能方程:
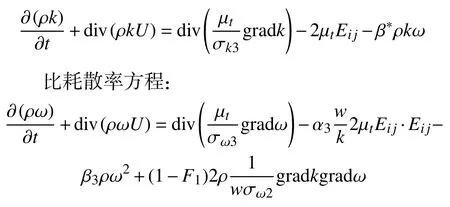
式中,各式系数根据Φ=F1ϕkw+(1−F1)ϕkε计算,即各系数为k-ω模型和修正k-ε模型相应系数的线性比例组合。

其传输行为可由包含限制数的涡流黏度方程求得
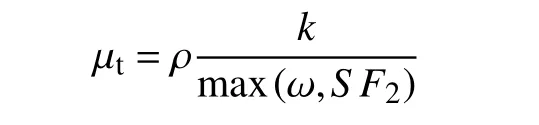
式中:F2为混合函数,由于模型中的假设不适用于自由剪切流动,该值确定了其限制范围;S为应变速度的不变量[13]。
2 模拟结果与分析
2.1 混合器内速度分布
图3 为水流量90 m3/h、空气流量10 m3/h 条件下水的轴面速度分布云图。两相流在进入静态混合器时,水的速度高于空气的速度,在黏性力的作用下,随着空气和水的混合,液相速度降低,气相速度增加,最终两相的速度趋于一致。
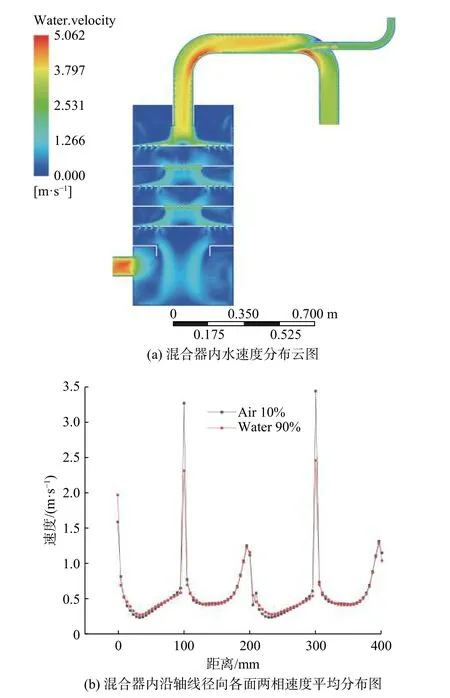
图 3 混合器内速度分布图
从图3(a)可以看出,在各级孔盘的相对上游,液体流速较小,当流体流经孔盘时,速度急剧增大,在各级孔盘的相对下游流速快速减小。其中孔盘上最大平均流速位于第3 孔盘。从图3(b)可以看出,最大流速水为2.46 m/s,气为3.44 m/s。孔盘的节流作用导致通孔内流速急剧升高,形成射流现象,并在节流孔盘相对下游形成了较大尺寸的涡流,但在一定程度上增加了气液两相流在器釜中的滞留时间,使两相流进行了相对充分的混合。
2.2 混合器内湍动能特性
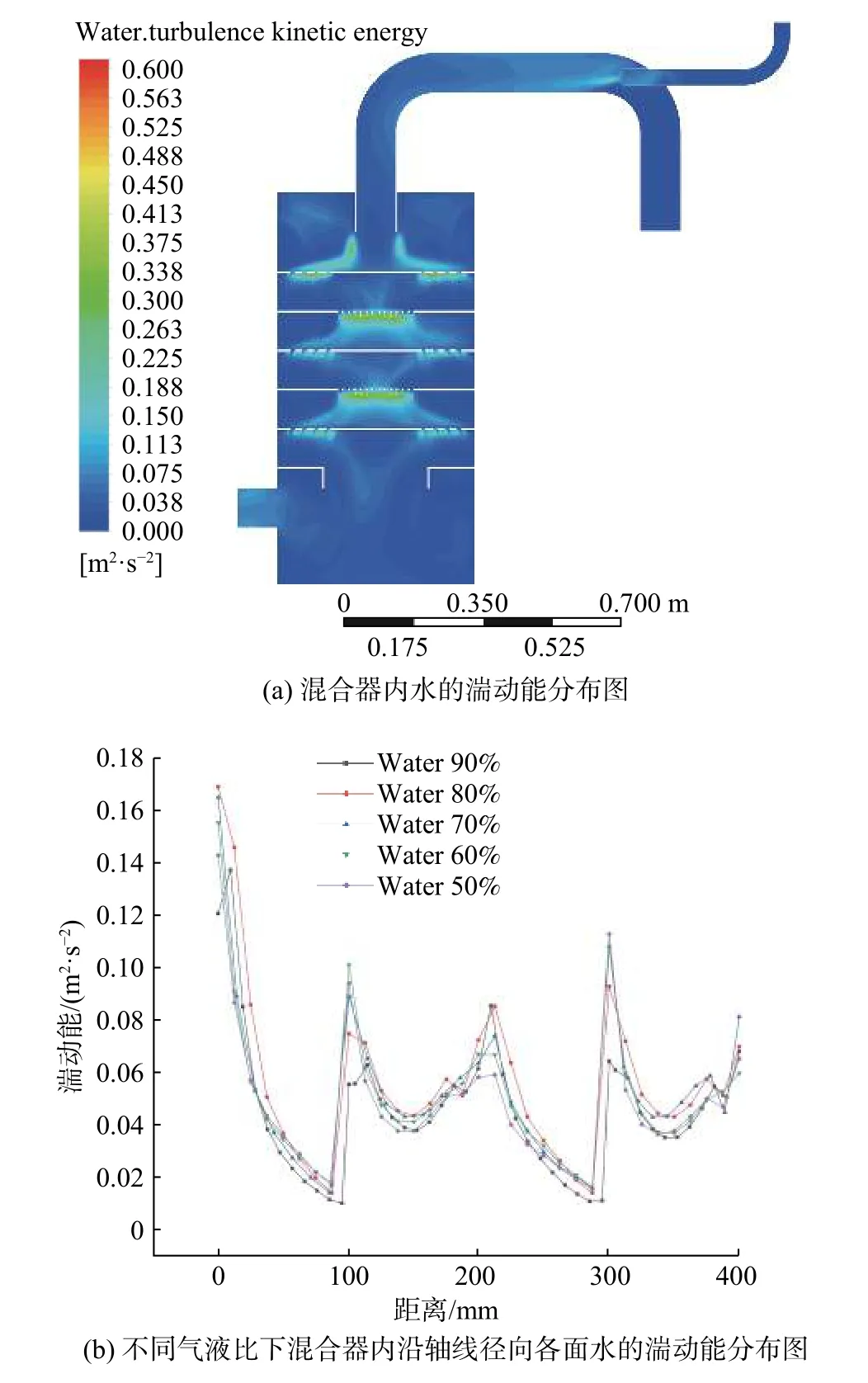
图 4 混合器内湍动能分布图
图4(a)示出总流量100 m3/h、体积流含液率90%时静态混合器湍动能沿轴线变化。由图4(a)可以得出:由于流体在孔盘通孔小截面流动中,雷诺数较小,水被层流化,导致流体的脉动速度小;当流体流出通孔后,压力变化大,流体在侧面的边界上与环境的流体之间形成了强烈的剪切,促使了流体流动的不稳定,在剪切层的粘性作用下降低射流外层流体的速度,同时也使环境中的流体运动起来;在高雷诺数的情况下,剪切层进一步转捩为湍流,使得流体通过孔盘后的湍动能比流体在孔盘中通孔的湍动能大。图4(b)为总流量100 m3/h、不同气液比下混合器内沿轴线径向各面的湍动能分布图。由图4(b)可以看出,在不同的气液比下湍动能沿轴线径向方向的变化趋势基本相同。流体在进入混合器经过每一个孔盘后,由于孔盘间压差变化不大(如图5(a)所示),对流体的流态扰动小,流体的湍动能在孔盘间沿程降低。
2.3 混合器内的压降特性
雷诺数是一种可用来表征流体流动情况的无量纲数,其公式为

式中:Re为雷诺数;ρ为流体密度,kg/m3;u为流体速度,m/s;L为特征长度,m。
计算雷诺数时参数中黏度和速度均采用加权平均[6],即:

式中:αg为气体体积分数;αl为液体体积分数;ug为气体速度,m/s;ul为液体速度,m/s;μg为气体动力粘度,Pa·s;μl为液体动力粘度,Pa·s。
体积流含液率为90%时,混合器轴面压力分布如图5(a)所示。从图5(a)可知,在每第一级孔盘相对上游,由于孔盘间距离较短,沿程流阻较小,所以每一级孔盘间压力基本不变。沿着流体流动的方向,在节流孔盘区域,由于节流孔盘的节流作用,强化了孔盘附近流体能量的耗散,导致了大部分静压转化为热能,使得压力急剧减小,形成了压力阶梯式下降的现象。
在保持总流量不变的情况下,通过改变气液两相流的入口速度来改变气液比和雷诺数。在等距离沿轴向径向方向检测各个截面上的平均压力,不同气液比和雷诺数下混合器内各截面压降沿轴线方向的变化如图5(b)所示。从图5(b)可以看出,在不同气液比下混合器内压降变化趋势基本一致,当体积流含液率大于50%时,器釜径向各截面压力均大于25 ℃时所对应水的饱和蒸汽压力3 169 Pa,没有发生空化现象。随着雷诺数的增大,体积流含液率增大,器釜径向各截面的压力也相对增大且总压降在增大。在雷诺数低的混合器中,压降变化小,在雷诺数高的混合器中,压降变化大,在每个相同结构的孔盘上局部压降基本相等。因此,总的局部压降可以认为是单个相同结构孔盘的局部压降与元件数的乘积。
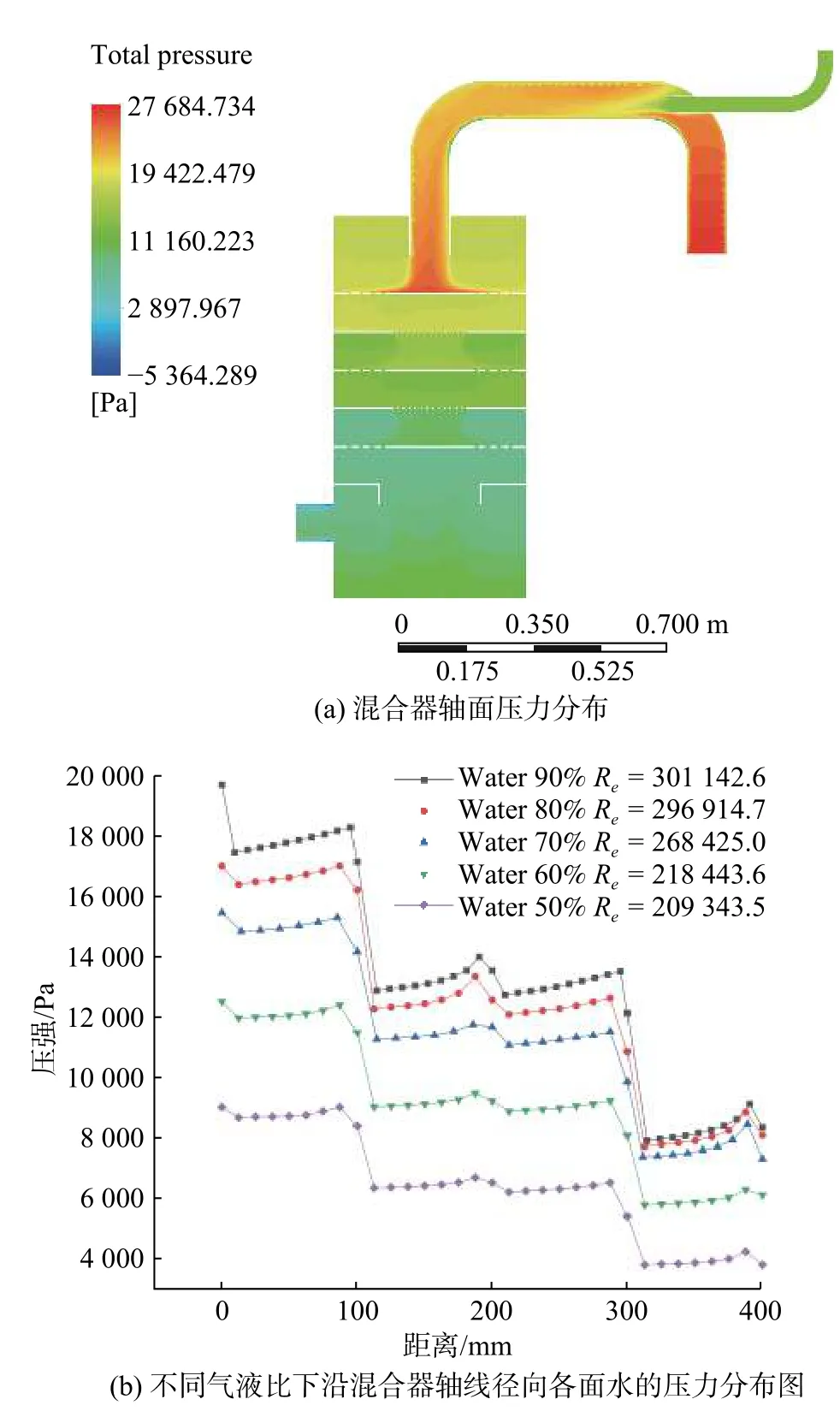
图 5 混合器内压强分布图
3 结 论
本文采用对一种具有孔盘式结构的静态混合器内气液两相流动进行了仿真计算,分析了该设备内部流场的流动与压降规律,得到下面的结论。
1)静态混合器内沿轴线的径向速度和湍动能分布显示,该设备对气液两相流在混合器中的流动混合具有促进作用,这样的促进作用是由孔盘的结构决定的,流体进入孔盘后,通过各层通孔强化相间的相互作用,实现了气液混合。
2)静态混合器内每个相同结构的孔盘上局部压降基本相等,因此总的局部压降可以认为单个相同结构孔盘的局部压降与元件数的乘积。
3)静态混合器内气液两相流的压降随雷诺数、体积含液率的增大呈明显增大趋势,当雷诺数大于268 425 时,两相流在混合器中压降更加显著。
