复合加载下油井管管柱的挤毁模型

2021-05-17郭克星袁雪婷田永强王维东于晨阳编译

焊管 2021年4期

郭克星，袁雪婷，董超，田永强，王维东，于晨阳，刘艺编译

（1. 宝鸡石油钢管有限责任公司，陕西宝鸡721008；2. 国家石油天然气管材工程技术研究中心，陕西宝鸡721008；3. 大连理工大学材料科学与工程学院，辽宁大连116000）

0 前言

在过去的几十年中， API 使用更精确的模型改进了对管柱性能的预测。美国石油学会（API）在相关标准中增加了一个公式，该公式考虑了管柱内部压力对挤毁强度的影响。 2015 年，API 技术报告的附录中添加了管柱基于三轴建模的挤毁强度预测公式，该公式更准确的预测了内部压力和轴向应力对挤毁强度的影响。 API 工作委员会通过同时进行内部压力的挤毁强度试验证明了该公式的有效性。

2013 年， API WG 2370 对API 挤毁预测公式进行了修正，以验证适用于三轴应力状态的试验。在外径为177.8 mm （7 in），等级为L80 的管柱上进行了24 次挤毁试验。挤毁试验分别在开放或封闭条件（OE/CE）下进行，使输入分别处于内部压力和无轴向载荷的三轴状态，并且分别给出内部压力和轴向应力的情况。相同的试验数据已应用于API/ISO TR 10400 中的Klever&Tamano （K&T）模型，并与API WG 2370 给出的结果进行了比较。

2018 年发布的API 报告中包含了2015 年发布的API 技术报告附录中的全部更新内容。它包括四个方程，这些方程根据外径（D）与壁厚（t）的比值以及材料的屈服强度来预测挤毁类型，挤毁的类型如图1 所示，分别为屈服强度挤毁、塑性挤毁、过渡挤毁和弹性挤毁。它们共同构成了所谓的“最小性能” 预测模型。

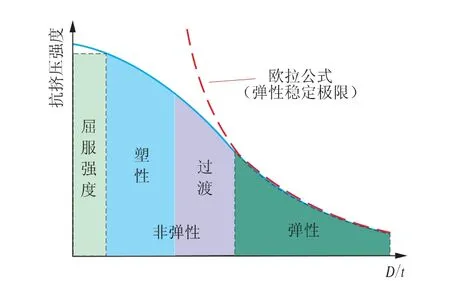
图1 API 规定的管柱挤毁类别

应用于API WG 2370 工作数据集的K&T 模型是API/ISO WG2b 在第5 指导委员会（SC5）下开发的，首次在API/ISO TR 10400：2007 中提出。 WG2b 对原有的K&T 模型进行了改进，并与其他10 个挤毁模型进行了比较，发现该模型是最准确的。 K&T 是一种极限强度模型（ULS），这意味着它可以预测管柱何时失效，对管柱挤毁的预测更准确，可以简化许多标准井套管的设计程序，并有助于降低成本和减少环境破坏。

1 管柱的抗挤强度预测

将最低性能模型的结果与极限强度模型（K&T）进行比较存在一些问题。最低性能模型内置了一些安全因素，而K&T 模型中没有这样的因素。有多种方法可以找到这些模型的“共同点”，其中两种明显的方法是消除API 模型中的嵌入式安全系数，或为K&T 模型添加安全系数。鉴于以下原因，本研究选择后者。

（1） API 挤毁模型与图1 中所示的四类挤毁预测并不一致。图1 中的四种类别管柱实际性能与API 挤毁预测模型之间的对比如图2 所示。

（2） API 模型输入三个参数（D、 t 和σs），均使用标准值。

（3） K&T 模型是利用统计学方法从多个材料参数中确定失效概率。

在不同的置信等级下调整K&T 模型的参数输入，然后比较实际挤毁数据与API 模型，可以了解API 模型中的嵌入式安全系数以及两种模型的准确性。

在当今的制造过程中，供应商能够控制管材的尺寸和力学性能。重要的尺寸特征，例如径厚比（D/t）、椭圆率和偏心率，对于抗挤毁性能至关重要。此外，影响抗挤性能的残余应力、屈服强度也可以通过热处理工艺得到控制，以确保最小的抗挤强度满足相关标准要求（如图2 所示）。

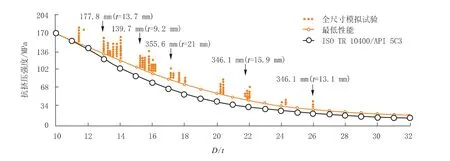
图2 管柱的实际抗挤性能和API 模型预测性能对比

1.1 API 挤毁模型预测

根据API 计算对挤毁进行建模需要以下步骤：

（1）通过D/t 和σs计算结果确定四个挤毁方程中哪一个与特定管材相关。

（2）如果D/t 和σs计算结果接近两个挤毁类型之间的极限，则应同时计算两者，并使用预测值最低的一个。

（3）计算值应理解为 “单轴”，即仅在管柱无轴向应力的情况下有效。

（4）对于具有内压、轴向应力或两者兼有的管柱，在确定挤毁极限之前，需要进行预计算，详见公式（1）。该公式更新于2015 年发布的ISO 10400： 2007 附录中。它的作用是修正屈服强度，以适应内部压力和轴向应力对所研究管材的挤毁强度产生的三轴效应。

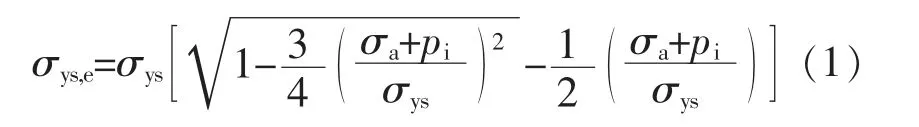
式中： σys——规定的最小屈服强度， MPa；

σa——非弯曲导致的轴向应力的分力， MPa；

pi——内部压力， MPa；

σys,e——组合载荷的等效屈服强度， MPa。

1.1.1 建模结果的分析

API 标准会议对目前的API 抗挤强度公式进行了详细的讨论，并在1968 年9 月发布的API 通告PS-1360 中进行了细致的报道。图3 是C75 级不同管柱的尺寸情况，说明了不同的API 挤毁类别。对于具有较高产量钢级管柱，方案之间的界限将降低到较低的D/t 值，反之亦然。

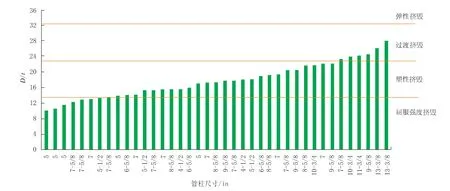
图3 C-75 钢级管柱尺寸及挤毁类型

1.1.2 屈服强度挤毁

屈服强度挤毁通常发生在小直径、大壁厚、高屈服强度的管柱上。由于超过屈服强度而导致的变形可能与在拉伸或压缩测试中经常看到的材料特定行为有关。根据Von Mises 屈服准则，导出了确定屈服强度破坏的公式。这意味着由屈服导致的管柱故障将仅限于图4 中标有黄色的椭圆区域内。

1.1.3 弹性挤毁

弹性挤毁遵循一种破坏机制，主要由与欧拉柱类似的不稳定性控制。 API 提出的屈服强度和弹性破坏预测公式均来源于理论推导。如图3 所示，由低屈服强度材料制备的大直径管柱通常是弹性挤毁造成管柱失效。由于弹性挤毁不受轴向应力的影响，这些管柱将限于图4 中标记为2 的水平线交叉点以及边界线。

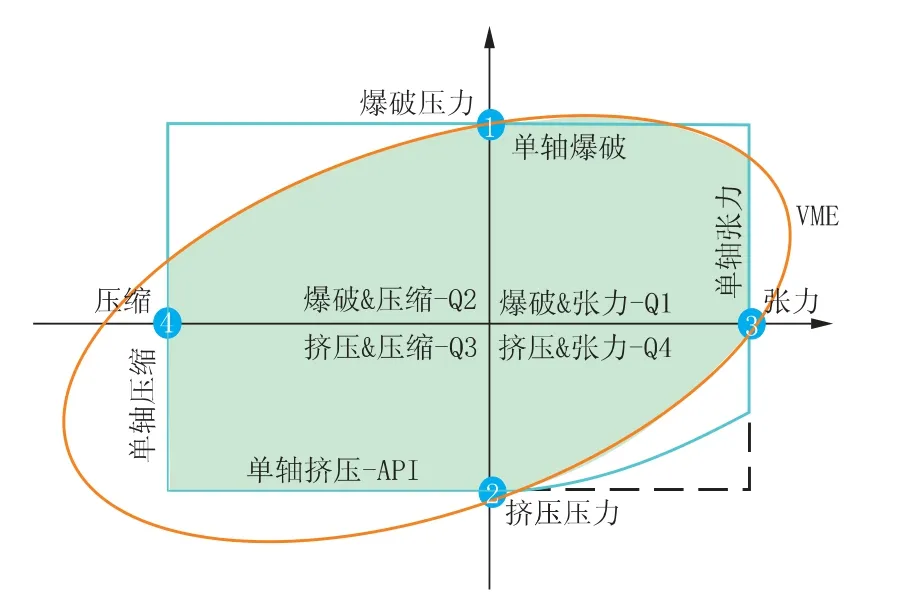
图4 三轴挤毁判定依据

1.1.4 非弹性挤毁-塑性和过渡挤毁

在材料科学中，屈服强度与弹性挤毁之间的区域是一个实体。但是， API 为 “过渡挤毁” 增加了理论范围，该范围用于推导管柱破裂的公式是经验性的。在20 世纪60 年代，塑性挤毁公式是根据在K55、 N80 和P110 级的管柱上进行了2 488 次挤毁试验得出的。由于试验是在没有轴向应力的情况下进行的，所以此时为单轴挤毁模型，如图4 中的点2。挤毁极限在第四象限呈曲线状，如图4 中点2、 3 之间的曲线。单轴值的计算见公式（2），该公式仅适用于张力计算。

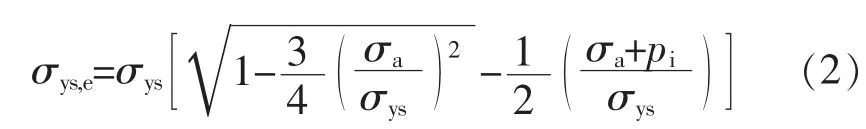
2015 年API/ISO TR 10400：2007 附录中增编了公式（2），由公式（2）到公式（1）的变更导致了三个重大变化：

（1）可以通过控制屈服强度来考虑内部压力对管柱抗挤毁性的影响。如Greenip 公式所述，假设内压和轴向应力对屈服强度产生的影响相等。

（2）将降低的屈服强度应用于传统的挤毁预测公式。

（3）三轴挤毁预测扩展到压缩在内。

在Greenip 的研究结果中，描述了Φ339.7 mm（133/8in） N80 管柱的公式（2）和公式（1）挤毁预测差异。该管柱的D/t 为26，这将使该管柱处于 “过渡挤毁” 段。上面第2 点中的一个重要注意事项是，当屈服强度降低约292 MPa时，发生过渡挤毁到弹性挤毁的潜在变化。

1.2 Klever 和Tamano 挤毁模型预测

软件模型中的理论来源于Tamano 等人，后来在2006 年与Klever 等人一起对模型进行了改进和修订。 API/ISO 工作委员会在对一系列调质管和非调质管进行了185 次的挤毁试验后，对模型进行了修正。首次在API 5C3/ISO TR 10400：2007 中提出，修正后的K&T 模型一致被认为是两个标准中预测挤毁最准确的模型。

修正后的K&T 模型能准确预测管柱的挤毁性能，因此是一个ULS 模型。抗挤毁性能由屈服强度、平均外径、平均壁厚、偏心率、椭圆度和残余应力共同决定。对测得的数据进行统计分析，使其呈现出概率分布。每个参数都有一个概率密度函数（PDF），这些参数在标准中的概率分布情况见表1。

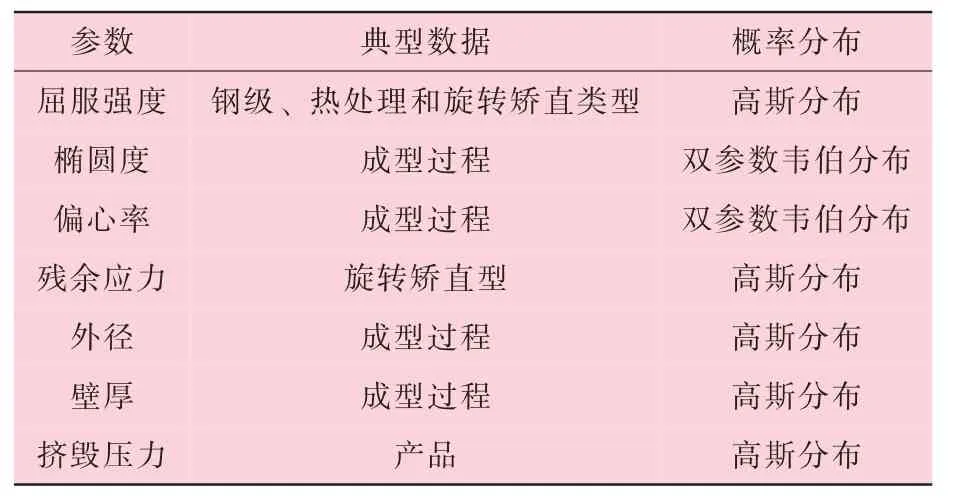
表1 每个参数的概率分布和典型数据

建立的K&T 挤毁模型考虑了三轴应力状态，因此选择正确的概率密度函数后无需进一步计算即可呈现出抗挤毁性能。从表1 可以看出，管柱的挤毁性能与图5 中的紫色线吻合。在进行管柱设计时，预期的最低管柱性能和最高的预期负载之间通常有一个裕度，如图5 所示。

图5 中显示为“隐含设计余量” 的差距也可以在图2 中看出，这取决于供应商的最低性能和API 挤毁性能。修正后的K&T 模型具有公式（3）所描述的“递减函数” 特性。

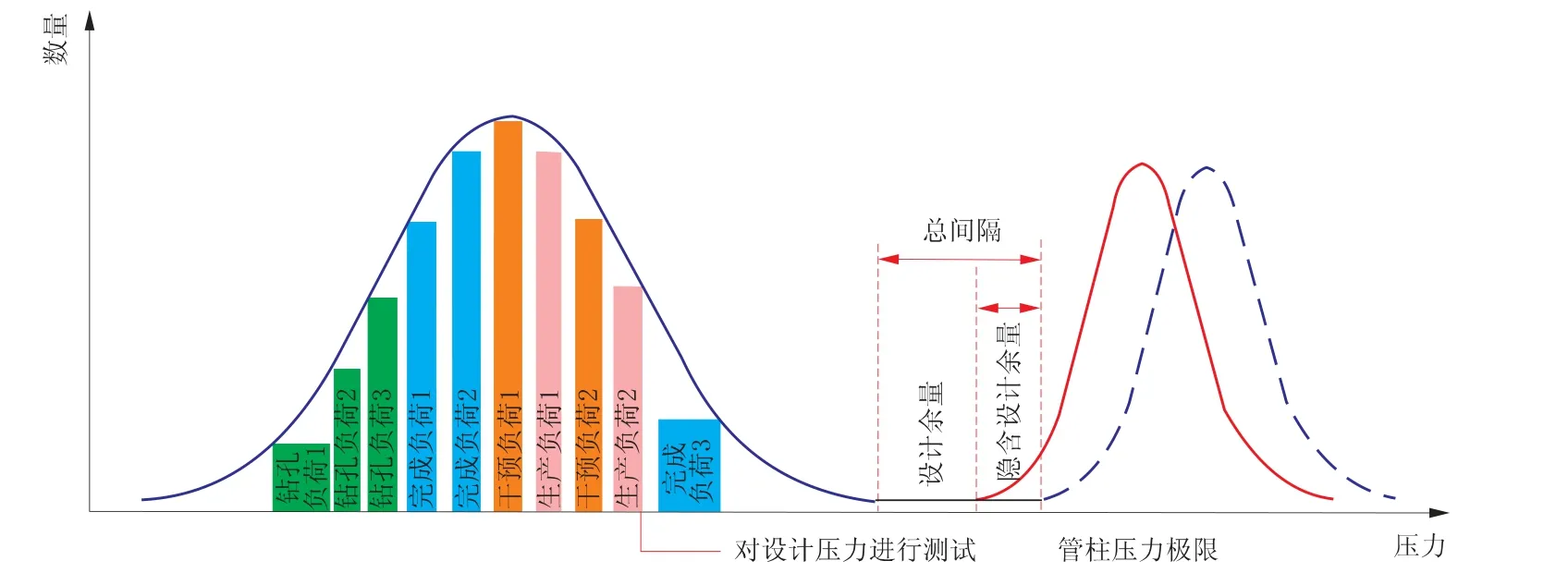
图5 复合加载、管柱性能安全裕度和管柱性能分布

式中： Ht——递减函数；

ov——椭圆度；

ec——离心率；

rs——残余应力， MPa；

σy——屈服应力， MPa；

hn——与低屈服强度钢的（典型圆形）拉伸试验曲线有关的因素。

递减函数描述了与抗挤毁性能相关的管柱物理特性的影响。为了获得具有代表性的值和真实的管柱性能，使用每个输入参数分布中的统计值来导出抗挤毁强度的概率分布，如图6 所示。

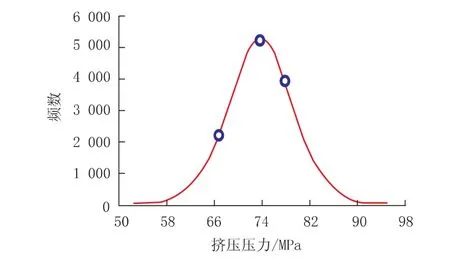
图6 P110 套管进行10 万次参数输入的挤毁预测的概率分布

使用管柱的具体性能将提供较准确的挤毁性能，即不是最低性能。利用特定管材特性进行单一预测，对被研究的管材将是准确的。考虑到对于表1 中列出的每一个参数，一批管材可能有不同的值，对这些参数进行基于概率的输入将产生更具代表性的抗挤毁能力。

API WG2b 收集了表1 中所列参数的大量制造统计数据。外径、壁厚以及6 000 个椭圆度和偏心率样品。分析了470 个热旋转矫直（HRS）样品和943 个冷旋转矫直（CRS）样品的残余应力测量结果，对P110 级套管进行了1 374 次拉伸测试，在此基础上绘制了屈服强度分布图。

在输入参数符合要求的情况下，管柱屈服强度分布如图6 所示，可以进行生产。挤毁的失效概率可以设置在任何期望的水平，例如2 个标准偏差意味着生产97.5%的管柱具有更高的屈服强度。此外，最高荷载和最低挤毁性能之间的设计系数通常为1.1，这为操作人员留出了足够的安全裕量。

2 管柱实际性能测试

表2、表3 列出了针对API 标准进行挤毁试验的结果和数据。挤毁测试是在L80 管柱上进行的，试验包含轴向应力。

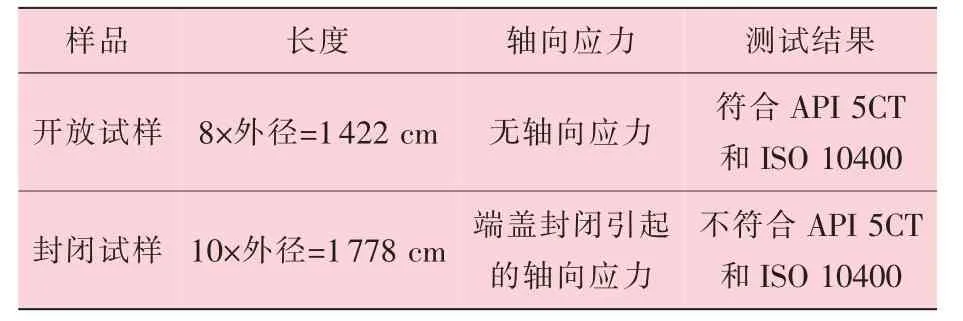
表2 开放试样和封闭试样的试验结果

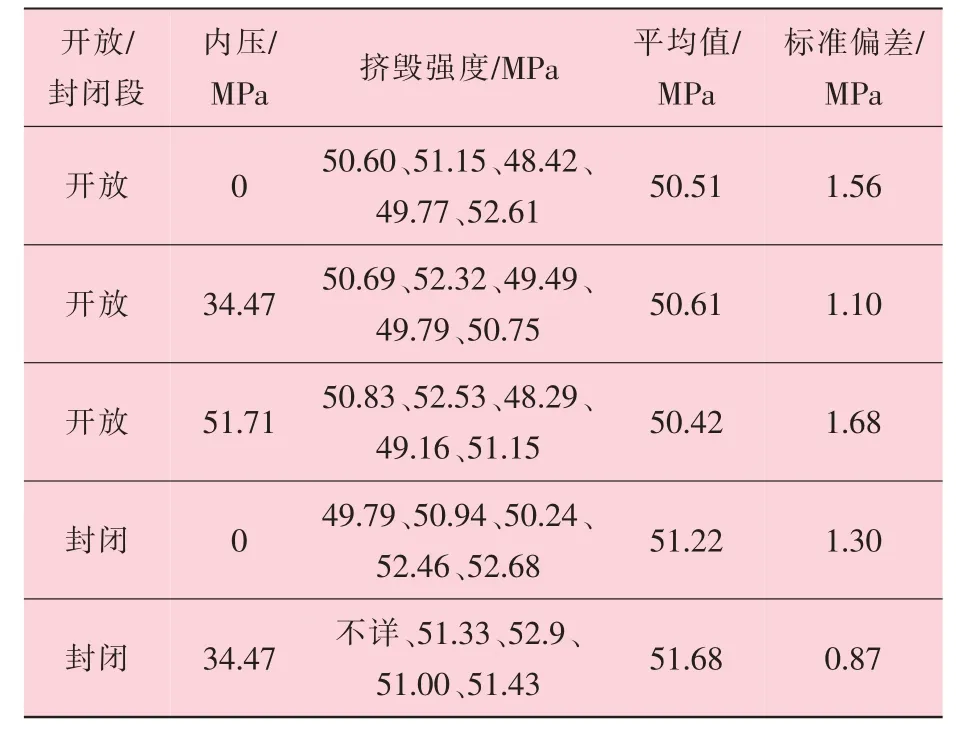
表3 API WG 2370 中的挤毁试验数据

模型的输入参数见表4，试验数据和相关的设备数据在Greenip 的研究结果中列出；壁厚的参数是根据Brechanetal 的建议进行有限元分析的结果；泊松比和弹性模量由套管材料决定；模型偏差因子选自ISO 标准（ISO/API-10400： 2007），其中使用了热旋转矫直的L80套管的值。由于大多数Q&T 管材的弯曲应力曲线都很尖锐，因此无需校正，并且形状常数设置为零（ISO/API-10400： 2007）。表4 中列出的用于定义其余输入的概率分布的参数源自（ISO/API-10400： 2007）中提供的HRS 套管的整体PDF。

通过应用随机数生成，使用列出的常数和概率分布进行了蒙特卡洛分析。该模型从每个概率分布中选择一个随机值，并使用相关的输入参数求解方程。重复此过程多次，以创建输出参数的概率分布。值得注意的是，在Klever 中讨论的“外部压力当量” 不适用在该分析中。

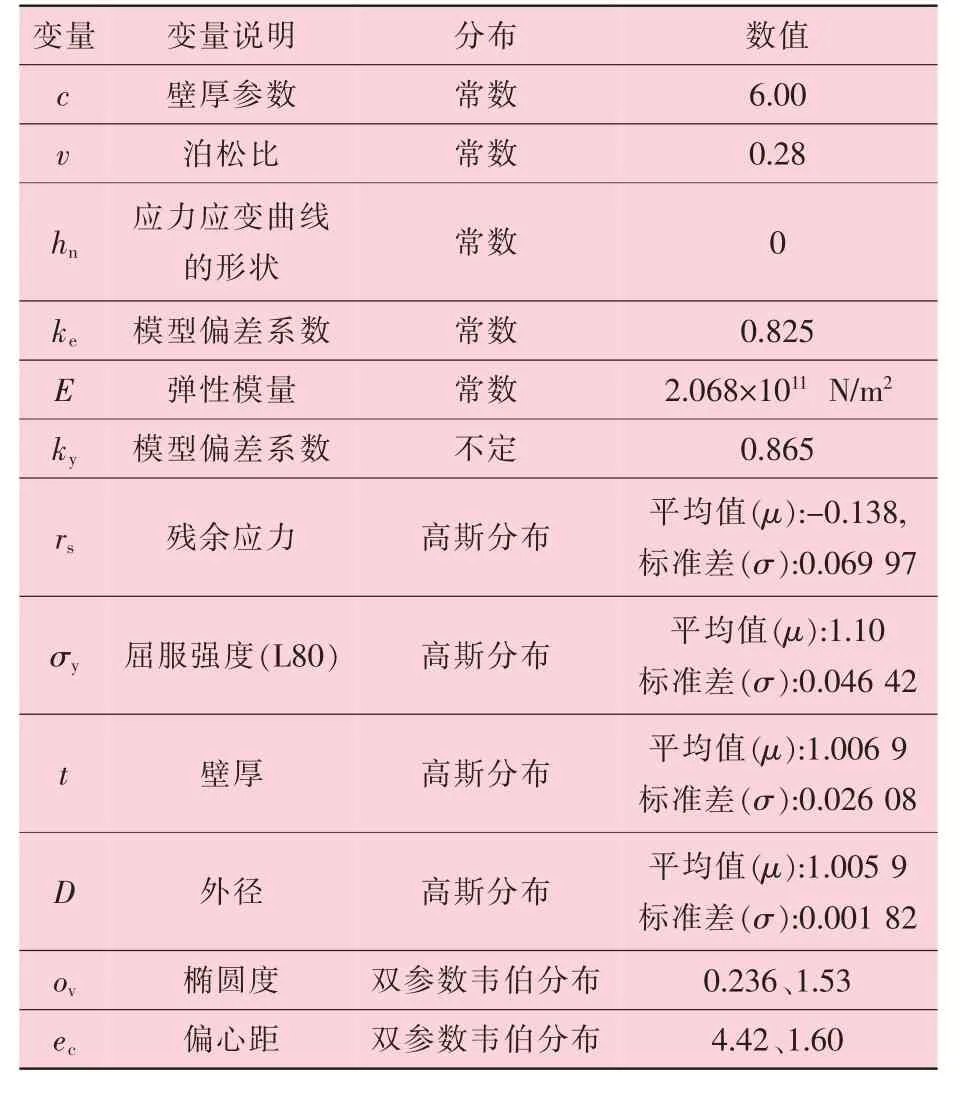
表4 K&T 模型中的参数

3 管柱挤毁预测结果与实测结果对比

实际挤毁结果如图7 所示。 x 轴上的试样编号与表2 中试样顺序相对应，即前15 个试样为开放式（OE），后9 个为封闭式（CE）。 API 标准预测的平均值如图7 所示。表5 为两种模型模拟值与试验值的相对差异。 API 模型的结果与K&T 模型的结果相差约3 个标准差。

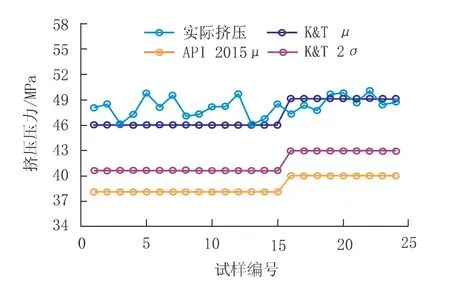
图7 管柱实测结果与预测结果的对比

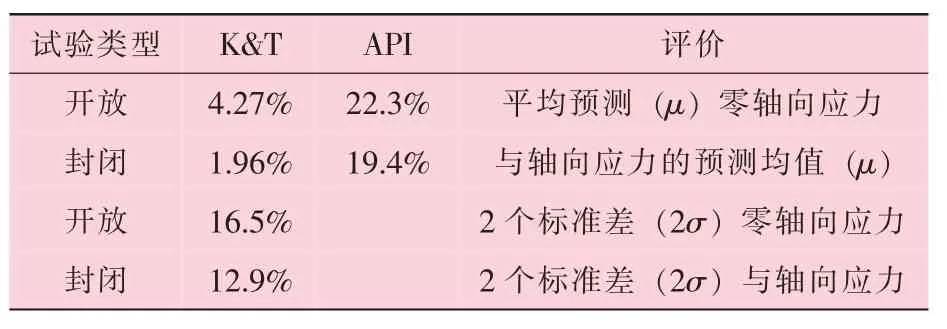
表5 两种模型模拟值与试验值的相对差异

4 讨论

API 在50 年前开发了行业标准挤毁预测模型。最常用的管柱属于塑性和过渡挤毁类别，对于某些管柱，其隐藏的安全系数为10%～35%。图2 中的曲线表示零轴向应力，所分析的试样是无缝的，热旋转矫直管不同于冷旋转矫直管的性能。每种材料的制造工艺参数K 和T 都是特定的， K&T 计算方法是最精确的极限强度模型，即预测每种管柱的实际挤毁性能。了解了材料的基本特性，就可以针对管柱将要承受的载荷进行安全系数设计。

在其他基于风险的计算中（例如防撞），即钻入另一口井或错过储层目标的风险，井眼测量精度行业指导委员会（ISCWSA）提出了两个标准偏差的安全级别。对于25 个试样中的第5 个试样，第5 个模型之间的平均差异为2 个标准差， K&T 挤毁预测减少42.12 MPa （6 109 Psi），降低16.6%， API 预测会减少0.36 MPa （52.3 Psi），降低22.3%， K&T 模型与API 模型在3 个标准偏差下重合。

估算其他管柱的影响可根据图2 推断，其中非弹性挤毁范围的嵌入设计裕度为15%～35%。使用K&T 或API 在2015 年API 附录中提供的三轴挤毁模型进行计算，对于了解管柱在役性能至关重要。由于采用最小性能法， API 挤毁预测不会区分管柱的制造方法或材料特性。因此可以得出结论，由于API 计算值与大型管柱生产厂家在图2 中所示的管柱实际最小性能之间的差距，K&T 和API 的挤毁预测值之间的差异将随D/t 范围和生产管柱的性能成比例变化。因此， ISO 10400/API 5C3 规定K&T 更精确，该方法在图2中的D/t 范围内更精确。