高强预压锚固技术抗拔力提升效应

2021-05-15杨渝南叶志强李洪亚

建筑材料学报 2021年2期

刘杰, 孙涛, 杨渝南, 叶志强, 李洪亚

(1.三峡大学三峡库区地质灾害教育部重点实验室, 湖北宜昌 443002; 2.三峡大学土木与建筑学院, 湖北宜昌 443002)

锚杆、锚索抗拔力不足是造成支护结构破坏的主要诱发因素.因此,如何有效增强锚杆抗拔力是国内外研究人员最关心的岩土锚固问题之一.

在锚杆抗拔力方面,国内外工程技术人员及学者进行了大量的试验及理论研究,且取得了可观的研究成果.Philips[1]给出了锚杆极限抗拔力公式,并计算出了相应的锚杆参数.Hyett等[2]通过室内模型试验及现场试验认为,适当降低水泥浆的水灰比,可以提高锚杆的极限抗拔力.Mostafa等[3]研究表明,锚杆剪切应力呈指数衰减，并提出了一种新的计算位移和剪切应力的解析解.Martín等[4]探讨了锚杆-浆体界面在拉拔环境下的力学响应过程和相关受影响因素.周密[5]推导了深埋式、浅埋式单盘锚杆和多盘锚杆的极限抗拔力计算公式.李哲等[6]根据已有理论提出了多段扩大头锚杆的抗拔力计算公式.梁月英[7]依据弹性力学理论,推导了扩孔压力型锚杆锚固体轴向应力及剪应力计算公式.王祥秋等[8]指出锚固长度等长时,扩孔锚杆的抗拔力是非扩孔锚杆的1.6倍.陆晓琴[9]基于Mindlin解探讨了主要影响扩孔锚杆极限抗拔力以及侧摩阻力的因子.刘国楠等[10]通过分析现场试验数据，对扩大头锚索的极限抗拔力计算进行了探讨.唐孟华等[11]通过锚杆的破坏性试验,得到了锚杆在中风化岩层中的剪应力分布规律,并给出了一种锚杆抗拔力的确定方法,可以为实际工程设计提供依据.

综上所述,目前对于锚固方面的研究多集中于探究锚杆类型或锚固方式对锚杆抗拔力的影响.通过在锚固体中加入5%～30%(质量分数)的膨胀剂,利用其膨胀性提高锚杆抗拔力的技术研究,目前未见相关报道.针对此,笔者提出了新型自膨胀高强预压锚固技术,并开展了高强预压锚固技术抗拔力提升效应研究.

1 自膨胀高强预压锚固技术原理分析

该新型锚固技术主要是将膨胀水泥浆体作为锚杆锚固体材料,通过锚孔周围土层来限制膨胀浆体的膨胀,以此产生径向的膨胀压应力,从而提高锚固体与土层界面的侧摩阻力.由于土层本身的弹塑性特性,在受到膨胀浆体膨胀产生的径向膨胀压应力后,锚固体本身的截面周长会增大,即产生扩头效应,增大锚固体与土层的接触面积,最终达到提高锚杆极限抗拔力的目的.

基于以上原理分析,定义抗拔力提升效应如式(1)所示.

λ=λ1+λ2+λ3

(1)

式中：λ为抗拔力提升效应;λ1为密实度提升效应,锚固体及周边受影响的土体抗剪强度参数在密实度提升的条件下得到大幅提升,密实度可以由CT值或者体应变进行表征;λ2为正应力提升效应,膨胀压应力将增大锚固体与锚杆、土体界面正应力,从而提升拉拔时的界面摩阻力;λ3为扩头作用引发的抗拔力提升效应.

本文主要对密实度提升效应λ1及正应力提升效应λ2作重点研究,篇幅所限,扩头作用引发的抗拔力提升效应λ3将另文叙述.

2 基于CT扫描技术的自膨胀锚固体及周围土层荷载传递机理研究

为定量研究λ1、λ2,采用笔者发明的基于CT扫描测定膨胀锚固体及周围土层密实度的试验方法(专利号：201811160702.0),以CT值表征密实度,以压应力片测试膨胀应力在径向和环向上的传递规律,开展定量获取CT值、径向和环向膨胀应力、体应变相互关系的研究.

2.1 试验步骤

(1)高强度侧限设置：利用高为40cm,直径为25cm的PVC管作为筒体,使用碳纤维布(2～3层)配合AB胶形成高强侧限,防止其中的水泥膨胀胀裂筒体.

(2)土体取样及压实：土样取自湖北省秭归县万古寺渡口旁土质边坡,主要以黄褐色或灰褐色粉质黏土为主,黏聚力为14.9kPa,内摩擦角为8.9°,在PVC管内预留孔后填土压实,并使土样筒内土体平均CT值达到1050.

(3)压力传感器布置：压力传感器埋入土样筒内圈层交界面(见图1).

图1 压力传感器布置Fig.1 Pressure sensor layout

(4)含膨胀锚固体的土样试件灌浆：将能消除CT扫描伪影的φ20×50cm玻璃纤维锚杆放入PVC管土样筒预留孔中心位置,以膨胀剂掺量(wE)分别为0%、5%、10%、15%、20%、25%、30%灌入土体中，得到膨胀锚固体的土样试件(见图2).

图2 含膨胀锚固体的土样试件Fig.2 Soil sample with expansion anchor solid

(5)膨胀锚固体试件灌浆：为更清晰掌握膨胀锚固体内部的密实度变化规律,将土样筒中的土全部置换为膨胀水泥,膨胀剂掺量同步骤(4).

(6)精准定位扫描：在土样筒周边布置扫描标记物(见图3),便于精准定位扫描.将试件同一横截面划分成半径为2.5,5.0,7.5,10.0,12.5cm的5个圈层(见图1),锚固体竖向上间隔30mm布置8个扫描面(见图4),养护21d后对锚固体进行CT扫描.

图3 膨胀锚固体试件Fig.3 Expansion anchor solid sample

图4 CT扫描面至交界面距离划分Fig.4 Distance division diagram of CT scanning surface to interface

2.2 锚固体不同交界面距离下CT值与膨胀剂掺量的变化规律分析

2.2.1不同膨胀剂掺量下锚固体CT值随扫描面至交界面距离的变化规律分析

图5为不同膨胀剂掺量下锚固体CT值随扫描面至交界面距离(c)的变化曲线.由图5可知：(1)同等条件下,膨胀锚固体CT值大于素水泥浆锚固体,最大相差25.4%,说明膨胀剂能大幅度提高浆体密实度,导致其抗渗能力和强度值相应增加.(2)当膨胀剂掺量为30%时,因为膨胀剂掺量过大,产生的膨胀压力超过该土体环境约束能力的极限值,土体出现裂纹,膨胀压力释放,同时导致膨胀锚固体内部孔隙率增大,密实度下降,CT值最高跌幅达199.

图5 不同膨胀剂掺量下锚固体CT值随扫描面至交界面距离的变化曲线Fig.5 Curves of CT value of anchor solid with the distance between the intersections of the scanning surface and the different content of expansion agent

2.2.2不同交界面距离下锚固体CT值预测公式建立

由图5可知,不同膨胀剂掺量下锚固体CT值A随扫描面至交界面距离的变化呈现指数变化趋势,具体计算公式见式(1).

A=aebc

(2)

式中：a为交界面锚固体CT值,hu;b为交界面距离对锚固体密实度的影响系数.

图6、7为不同膨胀剂掺量下的a、b值变化曲线.

图6 a值随膨胀剂掺量变化Fig.6 a value varies with the expansion agent content

图7 b值随膨胀剂掺量变化Fig.7 b value varies with the expansion agent content

由图6、7可见,锚固体顶层CT值随膨胀剂掺量呈现线性递增变化规律,密实度影响系数随膨胀剂掺量呈线性递增变化,其拟合公式如下：

a=247wE+1187

(3)

b=0.0018wE+0.0001

(4)

将式(3)、(4)代入式(2),得到不同膨胀剂掺量下的锚固体CT值与扫描面至交界面距离的关系,如下式所示：

A=(247wE+1187)e(0.001 8wE+0.000 1)c

(5)

根据式(5)可以在给定膨胀剂掺量及交界面距离下确定对应层面CT值.

2.3 膨胀锚固体及土体CT值随圈层变化规律分析

根据笔者提出的分圈层定量CT扫描技术(专利号：201610597318.1),根据式(6)可以计算出各圈层的CT值.

(6)

式中：AN为圈层n的CT值,hu;An为圈层n所在圆的CT值,hu;Sn为圈层n所在圆的面积,cm2.

以膨胀剂掺量25%为例,由于第1圈层为锚固体,故而建立圈层2～圈层5土体的CT值与到锚孔中心距离d之间的变化曲线，如图8所示.建立圈层1～圈层5膨胀锚固体CT值与到锚孔中心距离d之间的变化曲线，如图9所示.由图8可知,在土体中,CT值从内圈层到外圈层呈线性递减规律.由图9可知,在膨胀锚固体中,CT值从内圈到外圈呈线性递增趋势.对比图8、9可以发现,两者规律相反,为多层面解析膨胀锚固体及土体CT值随圈层变化机理,下面从锚固体及土层膨胀力径环向传递机理、体应变随圈层变化规律及体应变随CT值变化规律3个方面进行阐述.

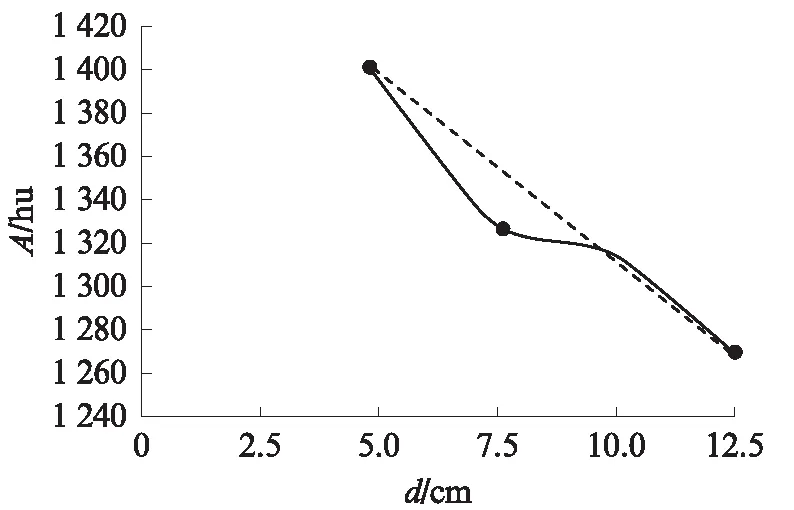
图8 土体CT值随圈层变化Fig.8 CT value of soil varies with circle-layer

图9 膨胀锚固体CT值随圈层变化Fig.9 CT value of expanded anchor solid varies with circle-layer

2.4 自膨胀高强预压锚固材料膨胀压应力在土体中传递规律及密实度分析

2.4.1土层径环向膨胀压力传递规律机理研究

2.4.1.1径向膨胀压力渐变规律分析

膨胀锚固体内环1,外环5(土层)这2个单元体的受力状态如图10所示.

图10 单元体内、外环受力图Fig.10 Force diagram of inner and outer ring of unit

由M1=M2=…=Mn静力平衡得：

σ1×l1=σ2×l2=…=σn×ln

(7)

(8)

式中：σ为膨胀应力；l为圆弧长度；γ为径向膨胀系数.

由式(7)、(8)知：因为S1σ2>…>σn,即从内环到外环所受径向膨胀压力(P)呈线性渐减的变化规律.

2.4.1.2径向膨胀压力测试结果与理论分析对比研究

定义Kn值为不同圈层径向膨胀压力实测值与理论值的差值,即Kn=|PMeasured-PTheoritical|(n=1,2,3,4,5).Kn值为土体非均匀性定量描述指标,图11为径向膨胀压力实测值与理论值插值随不同圈层的变化曲线.由图11可见：(1)膨胀锚固体所产生的膨胀压力在土体中从内环到外环呈现线性下降规律.(2)圈层3的Kn值最大,说明在实际试验中,膨胀锚固体的力在圈层2土体内传递较均匀,圈层3土体内的均匀程度较低并开始发生显著偏移,偏移值在0.25～0.50MPa.(3)理论值是在假定土体严格均匀条件下得出的,由于试验中土体存在不均匀性导致理论值与实测值存在偏差.

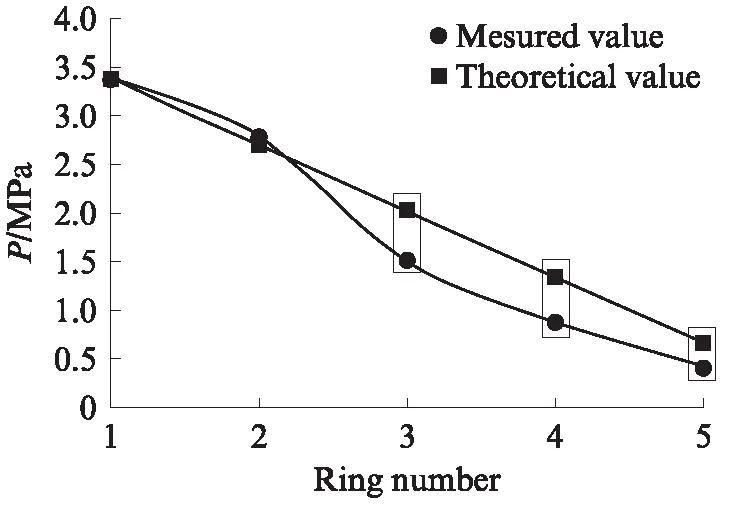
图11 径向膨胀压力随划分圈层变化曲线Fig.11 Radial expansion pressure curve with the division of ring

2.4.1.3环向膨胀压力渐变规律分析

外侧有约束自膨胀锚固体土体的受力状态如图12所示.

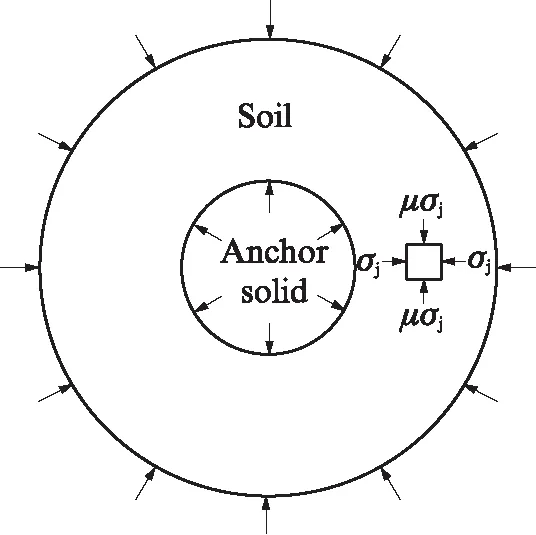
图12 有约束与有膨胀力状态受力图Fig.12 State diagram with constraint and expansion force

由泊松比公式可得：

(9)

式中：μ为土体泊松比;E为土体弹性模量;εh、εj为环向、径向应变；σh、σj为环向、径向应力.

由式(9)可知：假设土体是均匀压实的,因此土样筒内土体的泊松比相等,环向应变与径向应变比值为固定值(见式(10)),因此不同圈层的环向应力与径向应力变化规律应保持一致,如式(11)所示.

(10)

(11)

定义ρ为环向膨胀系数.

由于锚固体膨胀产生径向应力,土体径向上发生挤压从而产生次生环向应力.当土体均匀，其泊松比不变情况下,其环向应力和径向应力比值固定.根据式(12)推导出对应的环向膨胀压力随圈层变化曲线，如图13所示.由图13可见,土体环向膨胀压力随划分圈层变化与径向一样呈线性递减变化.

图13 环向膨胀压力随划分圈层变化曲线Fig.13 Curve of circumferential expansion pressure with dividing ring layer

σh=μσj=0.35σj

(12)

式中：μ为根据本试验得到的平均泊松比，0.35.

2.4.2基于圈层应力比的压缩面积分析

2.4.2.1膨胀锚固体外土体压缩面积分析

通过上述对径向、环向膨胀系数的分析,给出具体的算例分析.

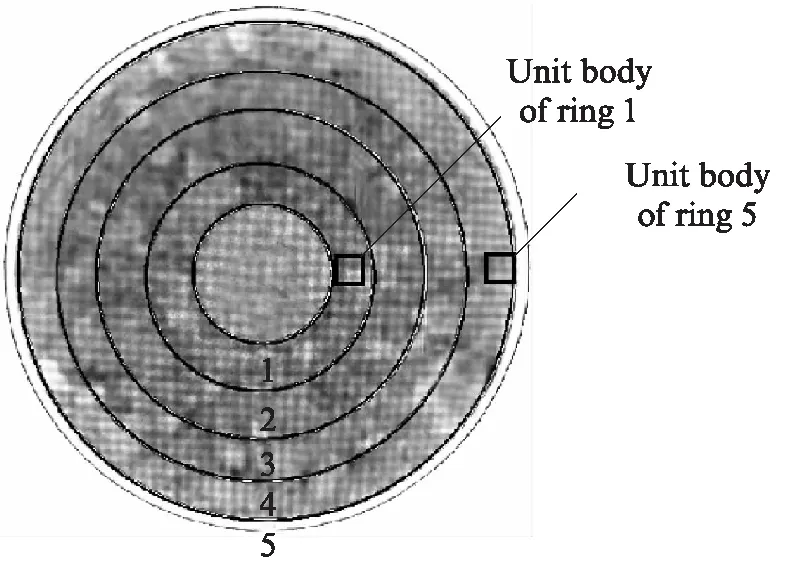
图14 锚固体外土体内外环单元体位置示意图Fig.14 Schematic diagram of position of inner and outer ring elements in external soil mass

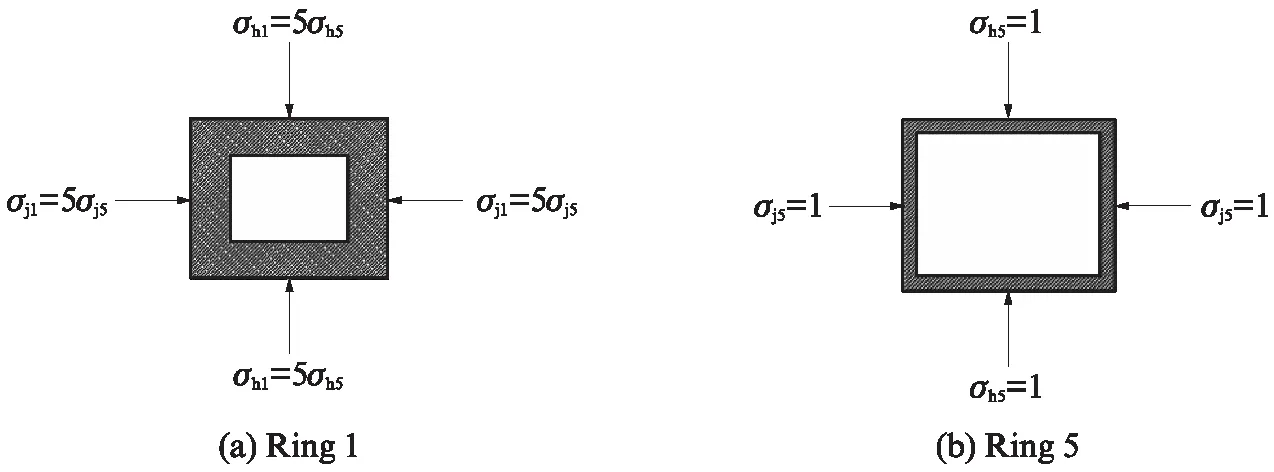
图15 土体内外环单元体受力示意图Fig.15 Stress diagram of inner and outer soil ring element

由图15可知，内环压缩面积：

ΔS=S1+S2-Δlj×Δlh=lh×
Δlj+lj×Δlh-Δlj×Δlh

(13)

外环压缩面积：

ΔS′=S′1+S′2-Δl′j×Δl′h=lh×
Δl′j+lj×Δl′h-Δl′j×Δl′h

(14)

式中：lh为单元体环向长度;lj为单元体径向长度;Δlh为内环单元体环向压缩长度;Δlj内环单元体径向压缩长度;Δl′h外环单元体环向压缩长度;Δl′j外环单元体径向压缩长度;S1为径向压缩面积;S2为环向压缩面积.

ΔS′-ΔS=S′1+S′2-Δl′j×Δl′h-(S1+S2-Δlj×Δlh)

=lh×(Δl′j-Δlj)+lj×(Δl′h-Δlh)+

Δlj×Δlh-Δl′j×Δl′h

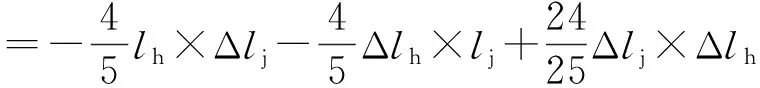
≪0

(15)

由式(15)可见：在锚固体发生膨胀之后，锚固体外土体外环压缩面积ΔS′≪内环压缩面积ΔS,进一步验证了膨胀锚固体外土体在同一层面上存在分环,表明膨胀压力及密实度在锚固体外土体从内环至外环呈线性渐降的变化规律.

2.4.2.2膨胀锚固体压缩面积分析

同理,通过对膨胀锚固体径向、环向膨胀系数的分析,给出具体的算例分析.得到：σj1′=5σj5′,σh5′=35σh1′.当膨胀水泥膨胀后，膨胀锚固体内、外环受力示意图如图16所示，其中外环单元体位置与图14所示相同.

图16 膨胀锚固体内外环受力示意图Fig.16 Stress diagram of inner and outer ring of expanded anchorage

同理,膨胀锚固体内外环压缩面积之差：

ΔS′-ΔS=S′1+S′2-Δl′j×Δl′h-(S1+S2-Δlj×Δlh)

=lh×(Δl′j-Δlj)+lj×(Δl′h-Δlh)+

Δlj×Δlh-Δl′j×Δl′h

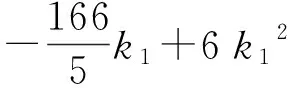
(16)

对比式(15)、(16)可知,膨胀锚固体外环压缩面积ΔS′≫内环压缩面积ΔS,与膨胀锚固体外土体压缩规律相反.

锚固体外土体中的膨胀应力由膨胀体界面传导而来,自膨胀锚固体则与之不同,其自膨胀应力是在锚固体内均匀产生的,该应力在边界上受到了最大的约束效应,使得环向上的应力增大35倍,形成了外圈层挤压密实度远高于内圈层的现象.

2.5 压缩体应变随圈层变化规律

2.5.1膨胀锚固体外土体应变变化规律

假设土体中E值处处相等,根据体应变公式(17)计算出各圈层的体应变.

(17)

式中：θ为体应变.

内环圈层1的体应变：

(18)

外环圈层5的体应变：

(19)

式中：μ为本试验测定的锚固体泊松比，0.15.

同理算出圈层2～4的体应变,并绘制体应变随圈层变化规律图(见图17).

图17 土体应变随圈层变化规律图Fig.17 Diagram of variation law of soil body strain with ring layer

由图17可知：锚固体外侧土体单元体的体应变随圈层变化规律严格按照圈层半径比从内圈到外圈呈幂函数下降趋势，如式(20)所示.

θ=16.87d-1

(20)

式中：16.87为体应变随其到锚孔中心距离的影响系数.

2.5.2膨胀锚固体各圈层体应变变化规律

同理可计算出膨胀锚固体各圈层体应变.

内环圈层1体应变：

(21)

外环圈层5体应变：

(22)

式中：S为压力传感器测力面积;F为压力传感器测得的压力.同理可算出圈层2～4的体应变并绘制体应变随其到锚孔中心距离d的变化规律图(见图18).

图18 膨胀锚固体体应变随其到锚孔中心距离变化规律图Fig.18 Figure of the variation law of the bulk strain of the expansion anchor solid with its distance to the center of the anchor hole

由图18可知：膨胀锚固体单元体体应变随圈层由内而外呈线性递增规律变化(见式(23)).

θ=0.72d+0.88

(23)

式中：0.72为体应变随其到锚孔中心距离影响系数;0.88为锚孔中心体应变.

2.5.3讨论

以上分别从锚固体及土体膨胀力径环向传递机理、体应变随圈层变化规律及体应变随CT值变化规律3个方面建立了膨胀力、体应变、CT值在不同土体层面上的演化模型,各模型之间相互印证、相互支撑.由于本文试验土样选自湖北省秭归县万古寺渡口旁土质边坡,因此本文计算公式的适用土体为粉质黏土.

上述分析表明：(1)在土体中CT值从内圈层到外圈层呈线性递减规律;(2)在膨胀锚固体中CT值从内圈层到外圈层呈线性递增规律.

3 抗拔力提升效应分析

高强预压锚固体系中自膨胀作用引发的密实度和正应力的提升效应是锚固体抗拔力提升的重要因素.根据上述算例对式(1)作定量表征,在土体锚孔中加了膨胀锚固体后,锚固体及周边土体内外环单元体密实度提升效应λ1示意如图19所示,锚固体及周边土体内外环单元体正应力提升效应λ2如图20所示.

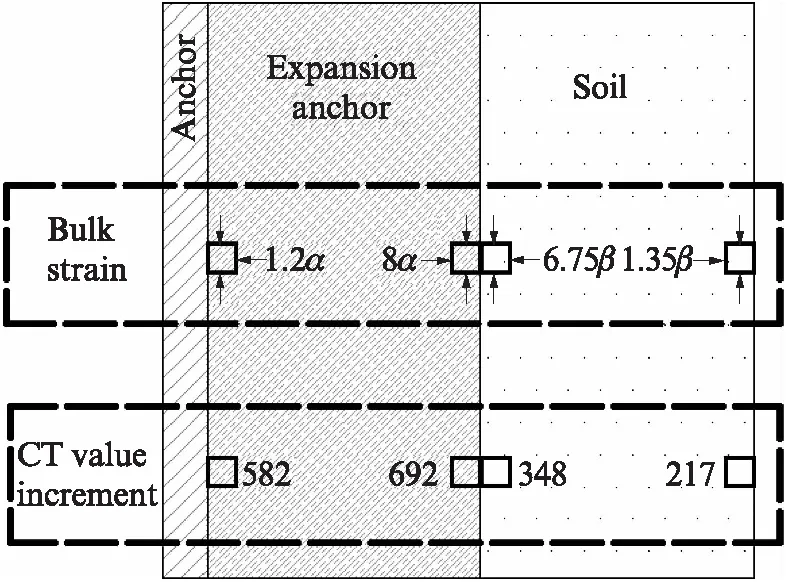
图19 密实度提升效应λ1示意图Fig.19 Schematic diagram of density enhancement effect λ1

图20 正应力提升效应 λ2示意图Fig.20 Schematic diagram of positive stress lifting effect λ2

图中各变量含义如下：

P=P0+ΔP

(24)

式中：P0为锚固体未施加膨胀剂时的初始应力,定为0;ΔP为膨胀应力导致锚固体自身及周边土体的附加应力,即图20中所示的正应力值皆为自膨胀应力引发的应力增量值.

(2)以土体外界面土体附加正应力ΔPt2为标准量,定义γt为土体附加正应力增长系数(见式(25)).

(25)

式中：ΔPt1为土体内界面附加正应力;ΔPt2为土体外界面附加正应力.

(3)以锚固体外界面附加正应力ΔPm2为标准量,定义γm为锚固体附加正应力增长系数(见式(26)).

(26)

式中：ΔPm1为锚固体内界面附加正应力;ΔPm2为锚固体外界面附加正应力.

由图19、20可知：当锚固体自膨胀应力施加后,体应变、CT值增量、界面正应力增量均会相应提升,且在锚固体及土体中分别呈相反的分圈层渐进变化规律,最终导致锚固体抗拔力大幅提升.

4 试验验证

为进一步验证高强预压锚固技术抗拔力提升效应,研究其抗拔力增加的机理,并最终形成一套切实可行的工程技术,在三峡库区地质灾害较为频发的区域开展了现场拉拔试验.

4.1 锚杆拉拔试验

(1)试验场地选取：现场试验地点选在湖北省秭归县万古寺渡口旁土质边坡,坡角60°,主要以黄褐色或灰褐色粉质黏土为主,黏聚力为14.9kPa,内摩擦角为8.9°,采用空压风钻机在土质边坡钻孔,钻孔深度为2m,钻孔直径为90mm.

(2)锚杆准备：试验选用锚杆为φ25三级螺纹钢筋,锚杆长度为2.5m,将压力传感器及导线用绝缘胶带固定在锚杆杆体上,以便随锚杆一同浇入钻孔内.

(3)灌浆、养护及现场锚杆拉拔试验：锚固长度设为60cm,膨胀剂掺量依次为0%、10%、15%、20%、25%、30%,每种掺量进行5组平行试验,水灰比取0.5.膨胀锚固体锚固段注浆完成后,在其上部灌注140cm普通水泥净浆,作为封口段,使膨胀锚固体处于封闭环境中,充分发挥其膨胀效果.自然状态下养护28d后开展拉拔试验.