水泥石灰石粉浆体颗粒水膜厚度与其屈服应力关系
2021-05-15张泽的韩凯东田承宇
肖 佳, 张泽的, 韩凯东, 田承宇, 邱 凯
(1.中南大学 土木工程学院, 湖南 长沙 410075; 2.中国水利水电第八工程局有限公司科研设计院, 湖南 长沙 410004)
水泥浆体的流变性能直接影响了施工操作时的难易程度及施工质量,并对浆体硬化后的力学性能、耐久性能有着重要的影响[1-2].屈服应力是表征浆体流变性能的重要参数,它指的是浆体发生流动所需要的最小剪切应力,屈服应力越小,浆体越容易发生流动.屈服应力主要由颗粒间作用力和水化产物的化学连接作用产生,水化初期主要受颗粒间作用力的影响[3-4].水泥浆体作为悬浮体,颗粒总比表面积、堆积密度等颗粒群特性对浆体屈服应力有重要的影响[1,5-6].石灰石粉掺入浆体中,由于其细度、掺量的不同,对颗粒群特性的影响不同,进而对浆体屈服应力的影响也不同.掺入水泥浆体中的细颗粒填充于粗颗粒之间,减小了颗粒之间的空隙,从而减少了用于填充空隙的水量,多余的水则润湿包裹在颗粒表面.同时掺入的细颗粒增加了颗粒总比表面积,减小了颗粒表面包裹层的厚度,具体表现为水膜厚度的变化[7],水膜厚度综合表征了颗粒堆积密度和总比表面积对浆体屈服应力的影响[6-7].Kwan等[8]研究发现,多余水比是影响浆体流动性的重要参数,但浆体的流动性同时受颗粒形状、细度的影响,水膜厚度与流动性之间关系的量化值得进一步研究.Li等[7,9]、Pui-Lam[10]和Kwan等[11]认为水膜厚度是影响砂浆新拌性能的最重要因素,并建立了砂浆工作性与水膜厚度、纤维因子(纤维体积、纵横比)的数学模型.Ye等[5]研究了水膜厚度对新拌浆体流动性的影响,建立了水膜厚度与相对流动直径和流动时间的定量关系.Vance等[6]研究发现,浆体屈服应力
随水膜厚度增大而减小,并以线性函数描述了二者之间的关系.以上研究多为水膜厚度对浆体工作性的影响,关于水膜厚度与屈服应力关系的研究较少,且已有的研究不够精细,多为定性描述二者间的关系.
本文通过标准稠度需水量试验测定颗粒堆积密度,并结合颗粒总比表面积来计算水膜厚度,同时采用旋转黏度计测定水泥-石灰石粉浆体的屈服应力,通过BP神经网络对测定数据进行训练并预测不同水膜厚度对应的屈服应力,建立了水泥-石灰石粉浆体颗粒水膜厚度与浆体屈服应力的关系模型,并对模型的准确性进行了验证.
1 试验
1.1 原材料及配合比
水泥(C)为中国联合水泥集团有限公司产P·Ⅰ 42.5拉法基瑞安基准水泥,其比表面积为347m2/kg.石灰石粉CaCO3含量(质量分数)为99%,比表面积分别为411、807、1007m2/kg,依次编号为LⅠ、LⅡ、LⅢ.水泥、石灰石粉的粒度分布如图1所示.水为自来水.水泥-石灰石粉浆体配合比如表1所示.

图1 水泥、石灰石粉的粒度分布Fig.1 Particle size distributions of the cement and ground limestone powder

表1 水泥-石灰石粉浆体配合比
1.2 流变性能测定

采用改性宾汉姆模型来描述水泥-石灰石粉浆体的流变行为,其表达式为τ=τ0+μγ+cγ2,其中τ0为动态屈服应力(Pa);μ为塑性黏度(Pa·s);c为二阶参数(Pa·s2).拟合数据的范围为下行段剪切速率在11~200s-1的区间.
1.3 计算公式
(1)水泥-石灰石粉浆体固体颗粒总比表面积(TSSA)[12]可由式(1)计算.
TSSA=ycmucm+ylul
(1)
式中:ycm、yl分别为水泥、石灰石粉颗粒的比表面积,μm2/μm3;ucm、ul分别为水泥、石灰石粉颗粒占固体总颗粒的体积分数.
(2)水泥-石灰石粉浆体固体颗粒堆积密度φ可由式(2)[13]计算.
(2)

(3)水泥-石灰石粉浆体颗粒水膜厚度(WFT)可通过式(3)[6-7]计算.
(3)
式中:uw′为多余水量与固体颗粒体积之比(多余水比);uw为水体积与固体颗粒体积之比;uvoid为空隙体积与固体颗粒体积之比.
2 结果与分析
2.1 水泥-石灰石粉浆体颗粒水膜厚度
图2为水胶比为0.38时水泥-石灰石粉浆体中固体颗粒总比表面积对水膜厚度的影响.由图2可见,随着固体颗粒总比表面积的增大,水泥-石灰石粉浆体颗粒水膜厚度先增大后减小,在总比表面积为1.113μm2/μm3处水膜厚度值最大.

图2 水泥-石灰石粉浆体颗粒总比表面积对水膜厚度的影响Fig.2 Effect of total specific surface area on water film thickness of cement-ground limestone powder paste
由式(3)可知:水泥-石灰石粉浆体颗粒水膜厚度为固体颗粒多余水比与总比表面积的比值,总比表面积的增大对水膜厚度有减小作用,多余水比的增大对水膜厚度有增大作用;多余水比由固体堆积密度决定,堆积密度越大,多余水比越大,因此水膜厚度的大小取决于二者作用的相对大小.
图3为固体颗粒堆积密度φ与总比表面积TSSA之比对水泥-石灰石粉浆体颗粒水膜厚度的影响.由图3可见,固体颗粒堆积密度与总比表面积之比越大,水泥- 石灰石粉浆体颗粒水膜厚度越大.结合表2可知,颗粒总比表面积为1.113μm2/μm3时,固体颗粒堆积密度与总比表面积之比达到最大,为0.51962.

图3 水泥-石灰石粉浆体颗粒堆积密度与总比表面积之比对水膜厚度的影响Fig.3 Effect of the ratio of packing density to total specific surface area on water film thickness of cement-ground limestone powder paste
由图3还可以看出,水泥-石灰石粉浆体颗粒水膜厚度的大小取决于固体颗粒堆积密度与总比表面积的比值.若以动态的观点看,不同水泥-石灰石粉浆体间水膜厚度的变化是固体颗粒堆积密度和总比表面积共同变化的结果,本文用固体颗粒堆积密度与总比表面积的相对增加速率来表征水泥-石灰石粉浆体颗粒水膜厚度的变化,结果如图4所示.其中ΔWFT表示水泥-石灰石粉浆体颗粒水膜厚度的变化率,用Δ表示固体颗粒堆积密度与总比表面积的相对增加速率,ΔWFT和Δ可采用式(4)、(5)计算,计算结果见表2.
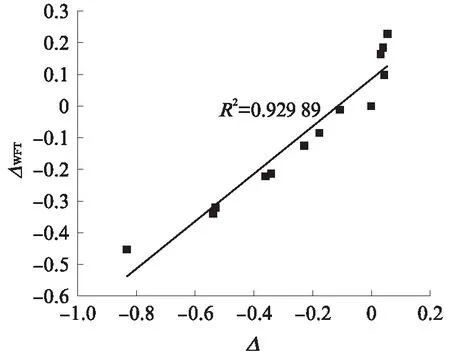
图4 水泥-石灰石粉浆体颗粒堆积密度与总比表面积的相对增加速率对水膜厚度变化率的影响Fig.4 Effect of relative increase rate of packing density and total specific surface area on variation of water film thickness of cement-ground limestone powder pastes
(4)
(5)
式中:WFT0为水泥净浆颗粒水膜厚度,μm;δφ为固体颗粒堆积密度的增加速率;δTSSA为总比表面积的增加速率;φ0为水泥净浆颗粒堆积密度;TSSA0为水泥净浆颗粒总比表面积,μm2/μm3.
由图4可见:水泥-石灰石粉浆体颗粒水膜厚度与固体颗粒堆积密度和总比表面积的相对增加速率有良好的相关性,随着固体颗粒堆积密度与总比表面积相对增加速率的增大,水泥-石灰石粉浆体颗粒水膜厚度变化率逐渐从负值变为正值;当Δ>0,即固体颗粒堆积密度增加速率大于总比表面积增加速率时,ΔWFT>0,水膜厚度增大;当Δ<0,即固体颗粒堆积密度增加速率小于总比表面积增加速率时,ΔWFT<0,水膜厚度减小.

表2 水泥-石灰石粉浆体颗粒堆积密度与总比表面积之比及相对增加速率
2.2 水膜厚度与屈服应力相关关系
图5为水胶比为0.38时水泥-石灰石粉浆体颗粒水膜厚度与浆体屈服应力(τ)的关系.由图5可见:浆体屈服应力与水泥-石灰石粉浆体颗粒水膜厚度呈负线性相关,随着水膜厚度增大,浆体屈服应力减小.原因是水泥-石灰石粉浆体颗粒水膜厚度增加了颗粒间距,减小了颗粒间作用力,同时颗粒表面的水膜有润滑作用,减小了颗粒之间的摩擦力[14],因此浆体屈服应力随水膜厚度的增大而减小.

图5 水泥-石灰石粉浆体颗粒水膜厚度与屈服应力关系Fig.5 Relationship between water film thickness and yield stress of cement-ground limestone powder paste
图5虽然描述了浆体屈服应力与水泥-石灰石粉浆体颗粒水膜厚度的关系,但更多是一种规律性描述,无法准确解释水膜厚度是如何影响浆体屈服应力的.基于此,本文采用旋转黏度计测定了水胶比为0.30的水泥-石灰石粉浆体颗粒水膜厚度和浆体屈服应力,结果见表3.同时,采用BP神经网络对水胶比为0.30和0.38的水泥-石灰石粉浆体颗粒水膜厚度、浆体屈服应力进行训练,其中水膜厚度为输入,浆体屈服应力为输出,预测水胶比为0.34和0.36时水泥-石灰石粉浆体的屈服应力,最终建立浆体屈服应力与水膜厚度的数学模型.

表3 水胶比为0.30的水泥-石灰石粉浆体颗粒水膜厚度、屈服应力

BP神经网络的实现主要有以下几步:
(1)设计输入、输出层.本模型以水膜厚度为输入、浆体屈服应力为输出,故输入输出层的神经元个数均为1.
(2)隐含层的设计.目前对于隐含层中神经元数目的确定并没有明确的公式,只有一些经验公式,本文在选取隐含层神经元个数的问题上参照了以下的经验公式:
(6)
式中:n为输入层神经元个数;m为输出层神经元个数;a为1~10间的常数.因此可知隐含层神经元个数在3~11之间,本文取5.
(3)激励函数的选取.选择S型正切函数tansig作为隐含层神经元的激励函数,S型对数函数logsig作为输出层神经元的激励函数.
(4)模型的实现.通过Matlab编程实现网络的训练与数据的预测,训练函数为traingdx,性能函数为mse,迭代参数设为5000,期望误差为0.0000001.
表4为BP神经网络预测结果统计.由表4可见,回归系数R均大于0.97,表明神经网络的预测值接近目标值,此过程中模型的预测精度很高.图6为某次预测过程中BP神经网络的总体效果图(R=0.99084).

表4 BP神经网络预测结果统计表

图6 BP神经网络总体预测效果Fig.6 Overall prediction effect of BP neural network
基于BP神经网络预测的浆体屈服应力数据和试验测定的水胶比为0.38和0.30的水泥-石灰石粉浆体颗粒水膜厚度与浆体屈服应力数据,研究了水膜厚度与浆体屈服应力的关系,如图7所示.由图7可见,浆体屈服应力与水泥-石灰石粉浆体颗粒水膜厚度有良好的相关性,可用半经验公式(式(7))来表达.

图7 水泥-石灰石粉浆体颗粒水膜厚度与浆体屈服应力关系Fig.7 Relationship between water film thickness and yield stress of cement-limestone powder paste
τ=k/(a+WFT)
(7)
由此可通过浆体颗粒水膜厚度近似计算浆体屈服应力.与图5对比后发现,采用线性函数来描述水泥-石灰石粉浆体颗粒水膜厚度与浆体屈服应力的关系并不准确.
采用旋转黏度计测定了水胶比为0.40的水泥-石灰石粉浆体颗粒水膜厚度、浆体屈服应力,通过对比浆体屈服应力的试验值和式(7)计算值的差异以检验上述半经验公式的准确性,对比结果见表5.运用SPSS统计分析软件对2组数据进行Peasron相关性分析,得到Peasron相关系数为0.955,双尾显著性检验值为0.003,表明二者相关系数的显著性水平在0.01以下,有统计学意义,从而证明上述半经验公式(式(7))具有较高的准确性.
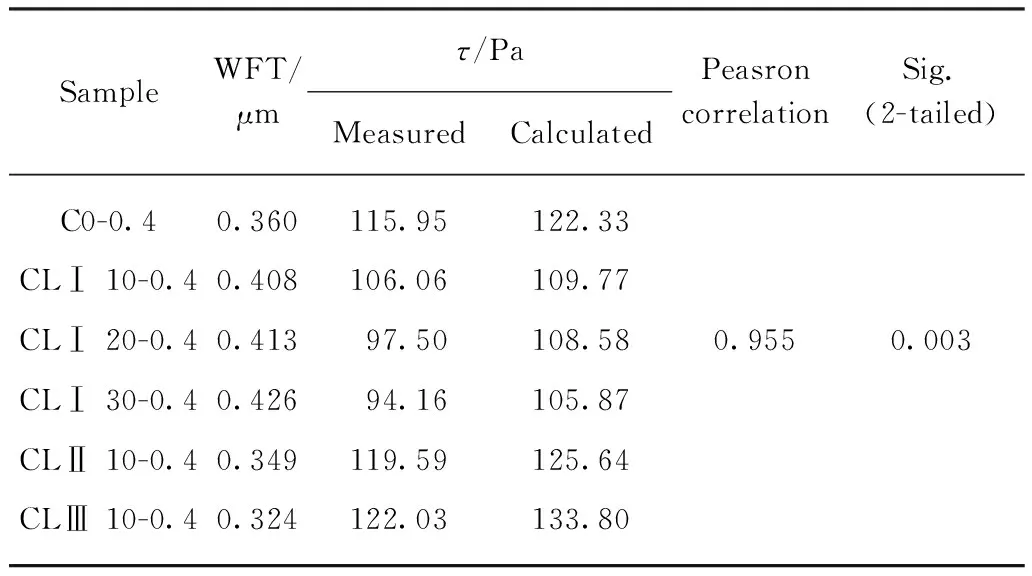
表5 水泥-石灰石粉浆体屈服应力式(7)计算值与试验值对比
3 结论
(1)随着固体颗粒总比表面积的增大,水泥-石灰石粉浆体颗粒水膜厚度先增大后减小,在总比表面积为1.113μm2/μm处的水膜厚度值最大.
(2)水泥-石灰石粉浆体颗粒水膜厚度取决于固体颗粒堆积密度与总比表面积之比,并随固体颗粒堆积密度的增大而增大;水膜厚度的变化与固体颗粒堆积密度和总比表面积的相对增加速率Δ显著相关,固体颗粒堆积密度增加速率大于颗粒总比表面积增加速率时(Δ>0),水膜厚度增大,反之水膜厚度减小.
(3)基于BP神经网络建立了水泥-石灰石粉浆体颗粒水膜厚度与浆体屈服应力之间的关系,可用半经验公式τ=k/(a+WFT)表达.公式计算值与测定值的Peasron相关系数为0.955,表明计算模型具有较高的精确度.
