从共线三球体碰撞问题的分析谈科学思维方法的训练

邹 斌 吴广国

(1. 中央民族大学理学院,北京 100081; 2. 北京景山学校,北京 100006)

科学思维是物理学科核心素养的重要组成部分．[1]如何通过物理理想模型的建构,如何科学合理的分析推理,怎样基于前人已有研究成果开展符合学术规范的论证研讨,并对不同观点与结论进行科学检验和修正,是需要物理教师在教学过程中深入思考和躬身实践的重要内容．共线三球体是三体问题中较为简单的理想模型,本文拟通过对该问题的分析求解,帮助学生正确理解经典物理学中弹性碰撞内容,并结合分析过程,浅谈如何对学生进行科学思维方法的训练．

以2020年北京高考物理试卷第13题(共线三球体问题,或称为三球牛顿摆问题)为例进行分析．已知编号分别为1号、2号和3号的三个完全相同的小钢球悬挂在同一竖直空间平面的同一高度处,初始时刻三只小球恰好能接触并且保持悬线平行,如图1所示．并且该体系中各悬线始终处于绷紧状态,各球之间都是对心正碰．

图1 共线三球体示意图

当1号球移到高度h后从静止状态释放,经过一系列碰撞后,可以观测到2号球静止,而3号球可以达到与1号球初始时相同的高度h．该题A选项创新性地提出,如果将中间的2号球换成质量不同的小钢球,并再次重复该碰撞实验,问考生3号球是否还能摆至高度h．

从该题所给条件可以判断出,三个完全相同的小钢球在最低点碰撞过程需要满足机械能守恒和动量守恒(即碰撞过程为弹性碰撞),否则3号球是不能摆到h高度的．分析该选项通常的思路是,在保证对心正碰的前提下,如果2号球的质量发生了改变,1号球和2号球的碰撞(后文记为“碰撞1”)会导致1号球碰后速度不为零．根据机械能守恒,2号球和3号球碰(后文记为“碰撞2”)后,3号球就不能获得足够的初动能,从而不能摆至高度h．因此似乎可以排除该题的A选项．

问题是,这样的思路是否可靠?在2号球质量改变后,该共线三球体问题是否只进行了1和2球之间及2和3球之间的两次碰撞?3号小钢球有没有可能从1号和2号球那里获得全部的动量(机械能),依然摆到h高度呢?

尽管该问题涉及到三个质点的运动和相互作用,但是这三个质点在各自最低点是共线的,我们可以反复利用二体弹性碰撞的思路逐次进行求解．需要指出的是,在理论上共线三球体问题中各球的碰撞次序是有争论的,各球递次发生碰撞和同时发生碰撞,其理论计算结果显然是不同的．[2]不过,陈小兵等人考虑小钢球的形变和密度参数,利用弹性体中的纵波关系给出碰撞作用力的传播速率为5.04×103m/s．[3]即使在毫秒时间间隔量级下,该数值也远大于小钢球的线度,因此实际发生的碰撞应认为是各球依次进行了碰撞．本文采用递次弹性碰撞的假设进行后续讨论．

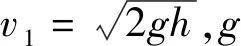
1号球从高度h处摆至最低点与2号球发生体系的第一次弹性碰撞(记为“碰撞1”),碰撞前后动量守恒和机械能守恒,有

v1+0=v1(1)+αv2(1)，

(1)

(2)

联立(1)式和(2)式得到

(3)

(4)

2号球与1号球碰撞后,与3号球发生第一次弹性碰撞,这是该体系的第二次碰撞,记为“碰撞2”．2号和3号球碰撞前后动量和机械能守恒,即

αv2(1)+0=αv2(2)+v3(2)，

(5)

(6)

联立(5)、(6)两式,有

(7)

(8)

1 关于时间间隔的讨论

本文上述理论模型中,各球之间的碰撞为弹性碰撞,时间间隔极短．问题是从1号球摆到最低点发生碰撞前开始,到3号球开始以v3(2)速率作圆周运动为止,经历的时间间隔具体有多长呢?“时间间隔极短”的提法有何依据呢?

由此还可以看出,尽管本文中1号、2号和3号小钢球有各自的悬线,各小球会绕各自悬点作圆周运动,但是时间间隔极短,在讨论问题时不需要考虑机械能中动能和重力势能的相互转化．并且上述论证过程也同时说明,本文所提到的碰撞满足文献[7]所要求的弹性碰撞条件．

此外,在这么短时间内的碰撞过程采用动量守恒或角动量守恒的观点进行计算,其结果是一致的．

2 关于α取值范围的3种情形

(1) 当α=1时,显然有v1(1)=v2(2)=0,v3(2)=v1．即经过”碰撞1”和“碰撞2”后,1号球和2号球先后静止,3号球获得了1号球的全部动量．这种情形就是题目中给的已知条件．

(2) 当α>1时,考虑到(1+α)2>4α,有v1(1)<0,v1>v3(2)>v2(2)>0．也就是说体系两次碰撞后,1号球向左运动,2号球和3号球向右运动,并且3号球摆动更快．由于3号球的速度小于v1,在“碰撞2”发生后3号球无法摆到高度h．该情形对应前文中提到的通常解决思路．

(3) 当0<α<1时,v1(1)>0,v2(2)<0,v3(2)>0,即此时1号球继续向右运动,而2号球向左,3号球向右．1号球和2号球将发生第二次碰撞(记为碰撞3)．下面我们主要讨论0<α<1的情况．

3 0<α<1情形的深入探讨

1号小球和2号小球的“碰撞3”过程依然满足动量守恒和机械能守恒,写为

v1(1)+αv2(2)=v1(3)+αv2(3).

(9)

(10)

将(3)式和(7)式代入上述两式,先消去v1(3),后联立(9)和(10)式求得

(11)

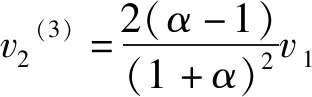
(12)

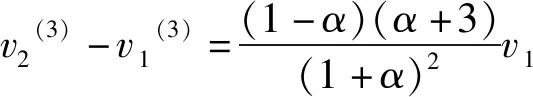
也就是说,在0<α<1情形下,考虑到各次碰撞时间极短,2号球将再次追上3号球,并与之发生第二次共线弹性碰撞(记为碰撞4)．

2号小球和3号小球的“碰撞4”过程动量守恒和机械能守恒可分别表示为

αv2(3)+v3(2)=αv2(4)+v3(4)，

(13)

(14)

需要指出,3号球第二次碰撞前速度大小取的是其第一次碰后速率,这是由于考虑两次碰撞(碰撞2和碰撞4)之间的时间间隔极短,3号球可认为作匀速直线运动,以下讨论思路与此相类似．

将(8)式和(11)式代入并消去v3(4),可以得到

(15)

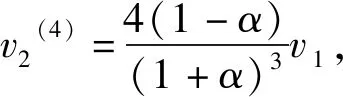
(16)

由(15)式和(16)式相减,可以得到

2]v1>0.

且有v3(4)>0．因此在“碰撞4”发生后,3号小球继续向右摆动,并且速率大于2号小球的速率．

如果令v3(4)=v1,则要求-4α(α+3)(α-1)=(1+α)4,经整理有

α4+8α3+14α2-8α+1=0.

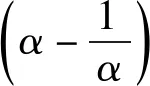
(α2+4α-1)2=0.

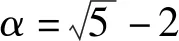
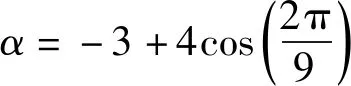
图2给出了2号球与3号球发生的前四次弹性碰撞后(也是与1号球发生了四次碰撞),要使3号球获得全部动量(机械能),其质量比α的取值情况．这里α的数值分别为1.0000、0.2361、0.1099和0.0642,其解析表达式见上文．由图2可以明显看出来,随着碰撞次数的增加,α的取值会衰减．可以预见,随着碰撞次数的增加,满足条件的α值将会趋近于零．

综上所述,共线三球体系统(三球牛顿摆系统)的2号球质量较大时,3号球肯定不能上摆到高度h处．但是,当2号钢球质量较小,且满足特定数值时(如图2所示),位于中间的2号球将与1号球和3号球发生若干次碰撞．最终通过2号球的能量传递,3号钢球获得该共线三球体系统的全部动量(机械能),从而有可能摆到高度h处．需要指出的是,只有α值为上述特殊取值,并且碰撞发生在递次弹性对心正碰撞体系这一严格限定性条件下,理论上3号球才能上摆到与1号球相同的初始高度．在一般情况下3号球还是无法摆至高度h的,因此题目中的A选项依然是要被排除的．

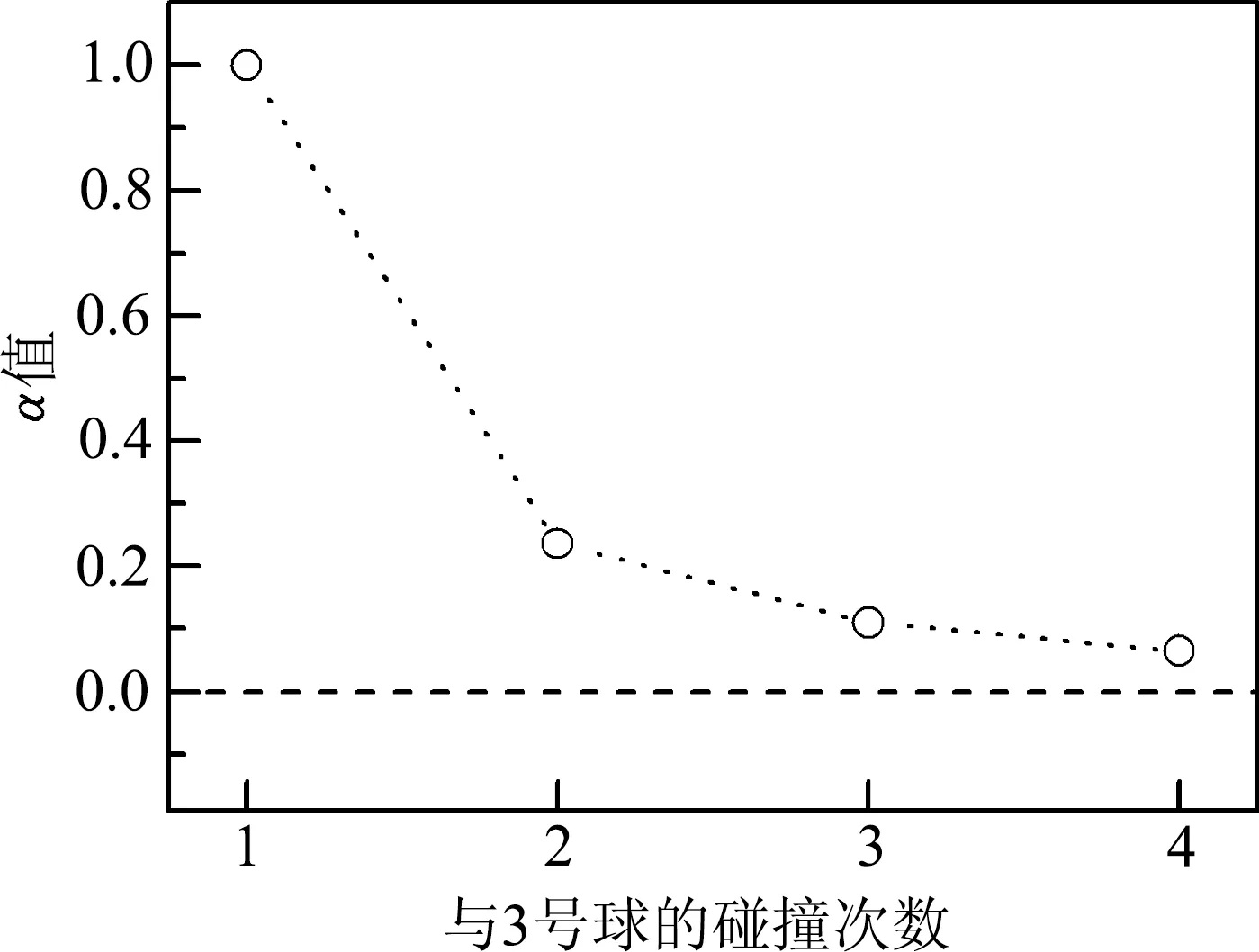
图2 不同碰撞次数情况下3号球能到达高度h处的α取值

本文对一类特殊的共线三球体系统(两端球质量相同,中间球质量有变化)进行分析讨论,可以很清楚地展示出如何借鉴他人的计算结果引入递次碰撞的假设,如何论证各次碰撞时间间隔极短,从而建立本文的计算模型;针对通常的分析思路,本文也给出了如何进行普通物理与初等数学水平下的理论检验和数据修正;本文还较为详细地展示了在弹性碰撞的前提下,通过动量守恒定律和机械能守恒定律的反复使用,如何进行推理和论证,从而得到右侧钢球也有可能达到相同高度地结论．此外,在引导学生一步步思考和论证共线三球体问题过程中,教师需要适当引申说明多体碰撞问题是当前机械工程、航空航天等关键领域的重要研究课题,这也是物理课程教学落实“立德树人”根本任务的重要一环．