蹦极者下落阶段运动规律的讨论
2021-05-15江俊勤邱为钢姜付锦
江俊勤 邱为钢 姜付锦
(1. 广东第二师范学院物理与信息工程系, 广东 广州 510303; 2. 湖州师范学院理学院,浙江 湖州 313000; 3. 湖北省武汉市黄陂区第一中学,湖北 武汉 430300)
1 问题的提出
蹦极或落绳(落链)下落阶段的运动规律与自由落体相同,还是比自由落体更快,一直存在不同的观点,例如某些奥林匹克竞赛物理教程或题选[1,2]认为落绳(落链)端点的加速度与自由落体加速度相同,a=g.

图1 蹦极过程示意图
第33届(2016年)全国中学生物理竞赛复赛的第四题给出了简单的解法和清晰的答案:蹦极者受绳子向下拉力作用,其加速度a>g.
复赛原考题:蹦极是年轻人喜爱的运动.为研究蹦极过程,现将一长为L、质量为m、当仅受到绳本身重力时几乎不可伸长的均匀弹性绳的一端系在桥沿b,绳的另一端系一质量为M的小物块(模拟蹦极者);假设M比m大很多,以至于均匀弹性绳受到绳本身重力和蹦极者的重力向下拉时会显著伸长,但仍在弹性限度内.在蹦极者从静止下落直至蹦极者到达最下端、但未向下拉紧绳之前的下落过程中,不考虑水平运动和可能的能量损失.重力加速度大小为g.
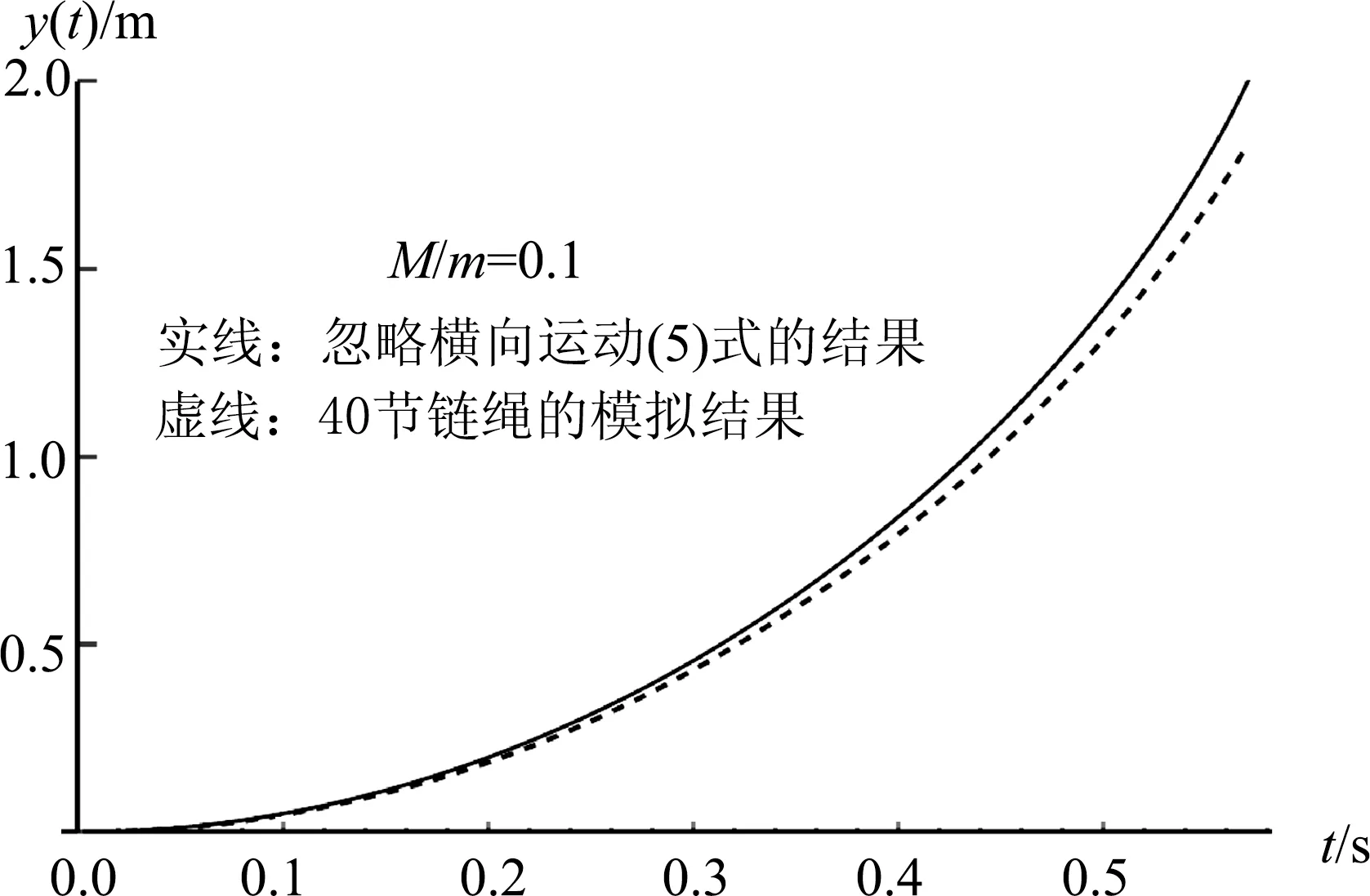
(1) 求蹦极者从静止下落距离y(y (2) 求蹦极者从静止下落距离y(y 试题问(1)的参考解答(有删节并补充注解): 取桥面为重力势能零点,系统初始能量是绳的初始势能(左半段势能不改变,不计入,M的初始势能为零),即 Ei=-mgL/4. (1) 蹦极者下落距离y时,系统的机械能为 (2) 按题意,不考虑可能的能量损失,Ei=Ef,有 (3) 将式(3)两边求导得 (4) (5) 加速度的上限大小为 (6) 至此,考题的原解应用机械能守恒定律巧妙地计算出了蹦极者加速度,但仔细考察以上的解答过程及其结果,我们发现有一些问题值得进一步讨论: (a) 当M=0(m≠0)时,ay→L→+∞,这显然是不符合实际的!问题出在哪? (b) 当M比m大很多(M/m≫1)时,a≈g, 蹦极者的运动与自由落体运动无明显差异(差异几乎可以忽略),这是合乎物理实际的;但是在这种情况下,绳子向下拉力(甩力)几乎可以忽略,本模型及其结果式(5)和式(6)的实际意义也就不是很大了. 如果在(a)和(b)两种极端情况之间的普通条件下,式(5)和式(6)仍然适用,那么该竞赛题的解法及其结果将具有更重要的意义,例如当M与m同数量级时式(5)和式(6)还适用吗?此时蹦极者的运动与自由落体明显不同(如取M/m=1,则ay→L=1.625g), 这种情况下研究绳子对蹦极者运动的影响才具有实际意义. 为了研究式(5)和式(6)的适用范围,下面我们考察在质量比M/m取不同值时,式(5)所描述的M(小物块或绳子自由端)的速度v和加速度a以及下落距离y(y 为了详细研究该竞赛题的解法及其结果式(5)和式(6)的适用范围(即研究质量比M/m在什么范围内式(5)和式(6)适用),可先求解体系动力学微分方程, 将式(5)改为微分方程形式并写出初始条件: (7) 式(7)在给出L、M和m的值后是一个定解问题,借助Mathematica就可得到蹦极者下落阶段的运动规律. 本文固定L=100 m,而M和m取多种不同的值. 不妨以M=55 kg和m=5 kg为例,求解式(7)可得蹦极者(以后简称M)到达最低点的时间为td=4.5009 s, 0~td时间内M的下落高度y,速度v和加速度a随时间t的关系如图2~图4的长划线所示. 在这种情况下蹦极者的运动规律与自由落体十分接近,下落到最低点的时间也与自由落体下落100 m的时间(4.51754 s)差别很小,这是合乎物理实际的, 式(5)和式(6)当然是适用的;但是蹦极者的运动规律与自由落体几乎无差异也反过来说明在M≫m条件下本模型的实际意义不大. 以M=m=55 kg为例,则M到达最低点的时间为td=4.37341 s,比自由落体快,绳的拉力(甩力)开始明显起作用,0~td时间内的M下落高度y,速度v和加速度a随时间t的关系如图2~图4的点线所示(曲线形态平稳).最低点的加速度a(t=td)=a(y=L)=1.625 g, 速度v=49.4975 m/s,大于自由落体的速度44.2719 m/s. 图2 3种不同情况下蹦极者(绳子自由端)下落高度y与时间t的关系 图3 3种不同情况下蹦极者(绳子自由端)下落速度v与时间t的关系 图4 3种不同情况下蹦极者(绳子自由端)下落加速度a与时间t的关系 这种情形最典型的例子就是没有蹦极者,纯粹的落绳,M=0,式(7)可进一步化简,它与m无关,描写的是绳子自由端处(为方便,下面仍称之为M)的下落规律 (8) 数值求解方程式(8)可得:到达最低点的时间为td=3.82732 s,比自由落体快得多,M的下落高度y,速度v和加速度a随时间t的关系如图2~图4的点划线所示(曲线形态异常:末端变化率几乎为无穷大).最低点的加速度a(y→L)→∞(a的极限值与L大小无关), 这显然是违背物理规律的. 对于M与m同数量级的情形,从图2~图4的点状曲线看,式(7)即式(5)的计算结果是合理的(曲线形态正常),初步认为考题的解法也适用这种情况. 为了检验上述论断,下面用有限元法对链绳的下落运动进行数值模拟. 表1 取不同M/m时,M到达最低点的高度和经历时间的模拟结果(L=2 m) 图时蹦极者下落高度y与时间t的关系(从开始至到达最低点两种结果的比较) 图时蹦极者下落高度y与时间t的关系(从开始至到达最低点两种结果的比较) 经过对考题原解法及其结果的分析,并用数值模拟进行了辅助检验,总结如下. (2) 考题的解法及结果式(5)和式(6)可以用于M与m同数量级的情况,蹦极者首次下落到最低点需要的时间可以通过解微分方程式(7)得知,若M=m, 取L=100 m,则蹦极者下落到最低点的时间td=4.37341 s,略短于自由落体的时间4.51754 s. 当然,由于考题的解法使用了简化模型,忽略了绳子的水平运动,式(5)~式(7)与实际结果之间必然存在一些误差; 有限元法的数值模拟可以研究蹦极者和落绳(落链)的真实运动,但过程比较复杂、计算量大.
2 加速度a、速度v和路程y与时间t的关系
2.1 M比m大得多(M≫m)的情形
2.2 当M与 m同数量级时
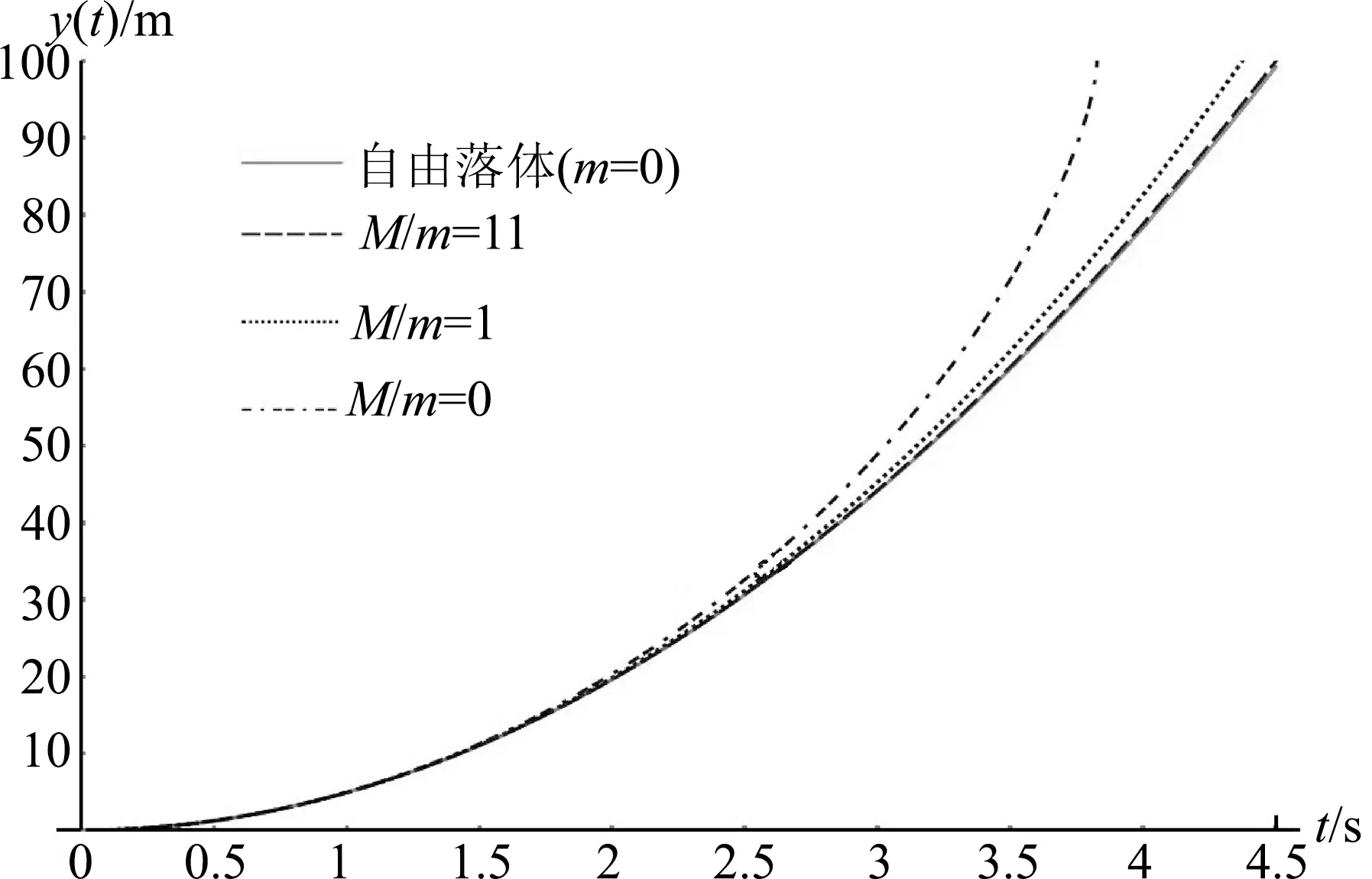
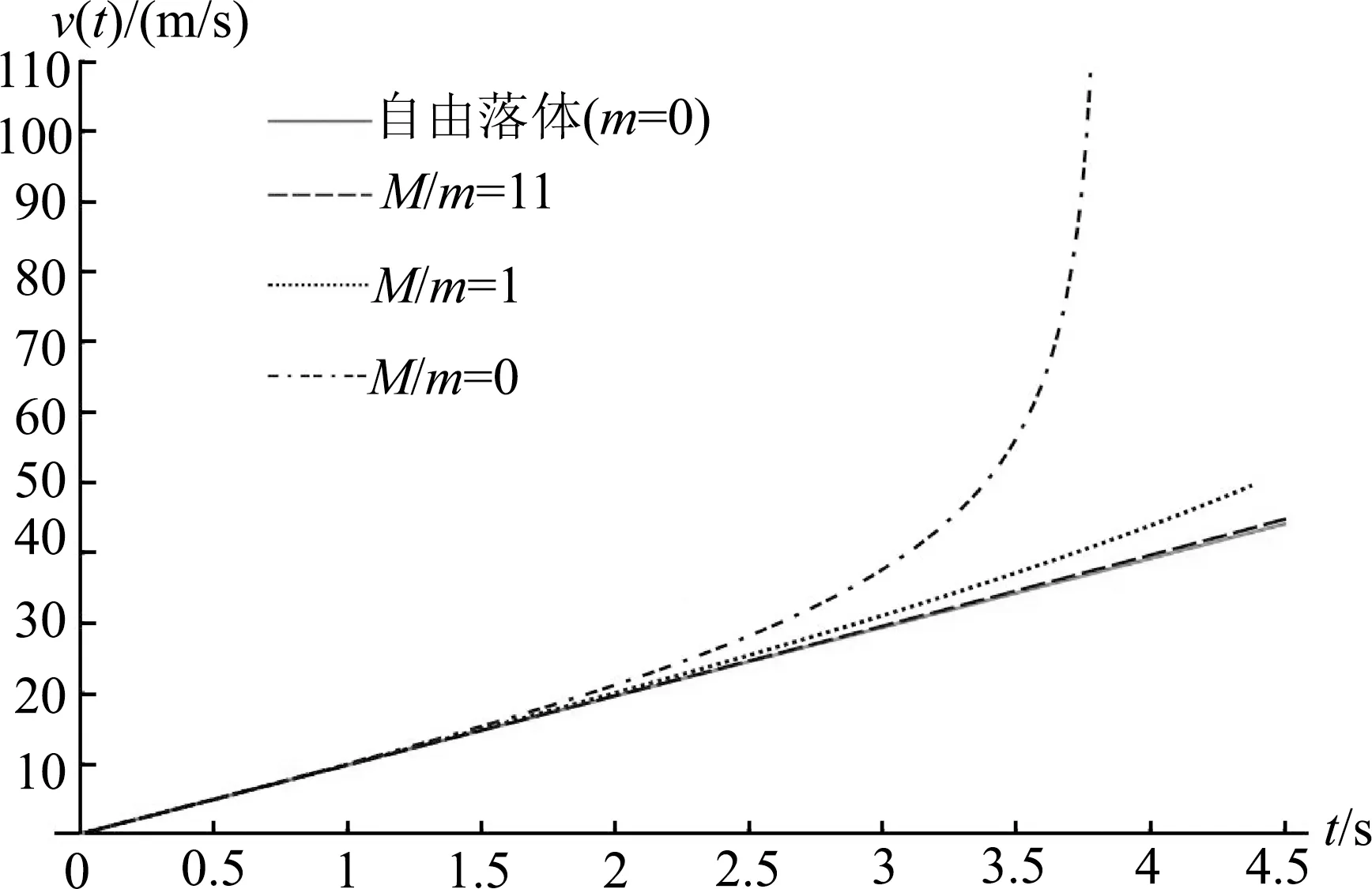

2.3 M比m小得多(M≪m)的情形
3 对考题答案适用范围的初步判断
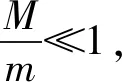



4 N节链绳下落运动的数值模拟






5 结论和讨论