鸢尾花数据集在随机向量数字特征中的相关应用
2021-05-15马淑兰
马淑兰
(宁夏师范学院 数学与计算机科学学院,宁夏 固原 756000)
多元统计分析是统计学中内容十分丰富、应用性极强的一个重要分支,它在自然科学、社会科学和经济学等各个领域中得到了越来越广泛的应用,是一种非常重要和实用的多元数据处理方法.它的内容从一元统计推广到多元统计,主要阐述了多元分布的基本概念及其统计推断,也涉及了多元统计独有的涉及降维方法包括:费希尔判别、主成分分析、因子分析、对应分析和典型分析[1-2].多元统计分析是指针对多元数据的统计分析方法,是同时考量多个变量,从多元数据集中获取信息的统计方法.在当前大数据时代,信息技术推动了可视化教学发展,借助计算机软件搜集可视化教学素材成为新的理工科教学理念的重要内容[3-4].R语言是新西兰奥克兰大学的Robert Gentleman 和Ross Ihaka及其他志愿者人员共同开发,主要用于统计分析、数据挖掘以及数据可视化,是一个用于统计计算和统计制图的优秀工具[5].RStudio是一款R语言的综合开发环境,使得R运行更加方便.本文以Fisher的鸢尾花数据集为研究对象[6],利用R语言对随机向量数字特征相关内容进行数据可视化,帮助学习者理解和掌握数学期望、协方差矩阵、相关系数矩阵等概念及性质.
1 随机向量数字特征
1.1 数学期望
p×q随机矩阵X=(xij)的数学期望定义为
特别地,当q=1时得随机向量x=(x1,x2,…,xp)′的数学期望定义,即
E(x)=[E(x1),E(x2),…,E(xp)]′.
1.2 协方差矩阵
设x=(x1,x2,…,xp)′和y=(y1,y2,…,yq)′分别为p维和q维随机向量,x和y的协方差矩阵定义为
可将其简写为
Cov(x,y)=E[x-E(x)][y-E(y)]′.
当x=y,Cov(x,x)称为x的协方差矩阵,记作V(x).
1.3 相关矩阵
设x=(x1,x2,…,xp)′和y=(y1,y2,…,yq)′分别为p维和q维随机向量,x和y的相关矩阵定义为
当x=y,ρ(x,x)称为x的相关矩阵,记作R=(ρij),其中ρij=ρ(xi,yj),ρii=1,即
2 多元数据数字特征的展示与可视化
2.1 数据来源
鸢尾花数据集(Fisher′s iris flower data set)由英国统计学家Ronald Aylmer fisher(费希尔)于1936年整理得到的,为了量化不同种类的鸢尾花形态上的区别进行收集的,它包含了三类鸢尾花数据:山鸢尾(Setosa)、杂色鸢尾(Versicolour)、维吉尼亚鸢尾(Virginica)的花萼、花瓣的长度与宽度.这个数据集是一个非常典型的多元数据集,共有150个不同种类鸢尾花的观测值,每一种鸢尾花的观察数据均为50个.数据集中的行代表了很多朵鸢尾花的样本,数据集中的每一列代表一个信息维度,共有五个信息维度即花萼的长(Sepal length),花萼的宽(Sepal width),花瓣的长(Petal length),花瓣的宽((Petal width ),鸢尾花的种类(Species).不同的鸢尾花在形态上有没有什么不同呢?这个问题给了Fisher研究多元统计分析方法的动机,面对这样一个数据集能做很多统计分析,比如变量之间的相关性分析,判别分析、回归分析等.生活中这样类似的数据集有很多,这也是利用该数据集做统计分析的原因.
2.2 基于R语言的数据结果展示与可视化
在多元统计分析中,相比一元随机变量数字特征的表达,多元数据的数字特征表达方式要复杂一些.在一元状态下,数学期望、协方差、相关系数等都用一个数值可以表示,而多元情况则用随机向量及矩阵表示.在R中调用colMeans函数对上述数据集中前四列变量求出数学期望,如表1所示

表1 三种鸢尾花前四个信息维度的数学期望
所求数学期望结果应记为(5.84,3.06,3.76,1.20).
在R中分别调用cov及cor函数即可得出前四列变量协方差矩阵及相关系数矩阵,如表2,表3所示.

表2 三种鸢尾花前四个信息维度的协方差阵
所求协方差矩阵结果应记为


表3 三种鸢尾花前四个信息维度的相关矩阵
以上是数字特征数值形式呈现,为了更好的解读数字特征在数据分布及其数据间相互依存关系中所起的作用,仍然以鸢尾花数据集前四个信息维度为例,利用R绘图功能以图形方式展现数据分布如图1所示,数据间两两相关程度如图2所示.
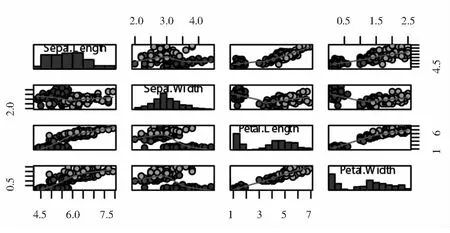
图1 三种鸢尾花前四个信息维度的分布直方图与两两散点图
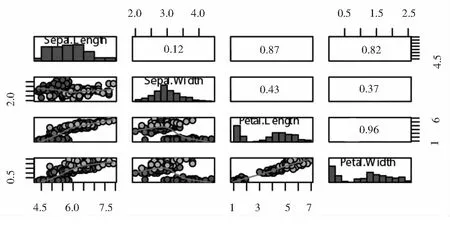
图2 包含相关系数的三种鸢尾花前四个信息的分布直方图与两两散点图
2.3 结果与分析
表1分别给出了鸢尾花数据集前四个变量数据的均值,即刻画了前四个信息维度的中心位置为(5.84,3.06,3.76,1.20),结合图1中的直方图分布图可以看出数据集里三种鸢尾花的花萼的长(Sepal length)、花萼的宽(Sepal width)、花瓣的长(Petal length)、花瓣的宽((Petal width )都分别向各自的中心位置集中.表2列出了鸢尾花数据集前四个变量数据的协方差矩阵数表,刻画了前四个信息维度的两两线性关系,结合图1中的二维散点图可以了解到四个信息维度数据的分散程度,利用图中的线性拟合曲线能看出花瓣的长(Petal length)、花瓣的宽((Petal width )线性关系最强.表3给出了鸢尾花数据集前四个变量数据的相关系数矩阵数表,这个数表理论上可以认为是协方差矩阵数表的标准化结果,将两两散点图的信息用[-1,1]之间的数去刻画,由于协方差矩阵的对称性,图2在图1的基础上把上三角的位置用相关系数填充,这样增强了图形的可视化效果,图2中上三角位置中的数据越大意味着其对称位置数据的线性相关性越强,譬如花瓣的长(Petal length)、花瓣的宽((Petal width )线性关系最强,相关系数为0.96.
3 结论
本文以随机向量数字特征理论为研究内容,以Fisher的鸢尾花数据集为研究对象,利用R语言强大的统计和绘图功能,完成了相关数据的展示和可视化,整个分析结果一目了然.“数缺形时少直觉,形少数时难入微”,在互联网和信息技术突飞猛进的背景下,数据的可视化充斥在生活的方方面面,利用理论知识和实用的计算机软件,提炼数据隐含信息、挖掘其统计规律并对其发展规律进行预测分析将成为数据分析的关键内容.
