基于商密SM9 的高效标识签密*
2021-05-15赖建昌黄欣沂何德彪
赖建昌, 黄欣沂, 何德彪, 伍 玮
1. 福建师范大学 数学与信息学院 福建省网络安全与密码技术重点实验室 福建省应用数学中心, 福州350007
2. 武汉大学 网络安全学院 空天信息安全与可信计算教育部重点实验室, 武汉430072
1 引言
互联网、量子计算、云计算、区块链等技术的发展和应用离不开加密和签名等密码技术的保障. 数据加密能有效保护数据的私密性, 数字签名可以保证数据的完整性和真实性, 以及签名者的不可否认性. 用户可根据应用的需求选择不同的密码技术. 当同时需要签名和加密时, 采用先签名后加密的方法会增大计算开销, 同时增加密文长度, 效率较低. 为了有效解决该问题, Zheng[1]在1997 年美密会上提出签密的概念. 一次签密运算就能同时实现签名和加密的功能, 只有知道接收者的私钥才能正确解密出签名的数据,进一步验证签名的有效性. 与先签名后加密的方法相比, 签密能显著减少计算开销和通信代价.
传统公钥密码体制需要第三方机构为每个用户颁发证书, 绑定用户公钥和身份, 确保用户公钥的真实有效性. 然而证书存在管理问题, 且证书的验证开销较大, 不适用于传感器、智能卡等计算资源有限的设备. 为了解决证书问题, Shamir[2]1984 年提出标识密码系统(Identity-Based Cryptosystem), 也称为基于身份的密码系统. 在标识密码系统中, 用户的公钥可以是邮箱地址、手机号码等能唯一标识用户的任意字符串, 相应的私钥由密钥生成中心(Key Generation Center, KGC) 统一计算. 标识密码系统消除了证书, 有效解决了证书的验证和管理问题. 自标识密码概念提出后, 标识密码得到国内外学者积极的研究, 但直到2001 年, Boneh 和Franklin[3]利用基于椭圆曲线的双线性对(Pairing over Elliptic Curves)技术提出第一个实用可证明安全的标识加密方案. 接着, 不同性能的标识密码方案被大量提出[4–11]. Malone-Lee在文献[12] 中将标识密码体制拓展到签密系统, 并提出实现标识签密的有效方法. 随后, 标识签密在文献[4,13–18] 中得到了进一步的研究.
虽然标识密码得到了广泛的研究, 取得了积极的进展, 但从整体上看, 标识密码研究大多围绕国外提出的算法展开. 秉承着核心技术自主创新、信息安全自主可控的理念, 我国积极推进标识密码算法的研究,自主设计了包括数字签名算法、密钥交换协议、密钥封装机制和公钥加密算法的SM9 标识密码算法[19].2016 年3 月, 国家密码管理局正式发布《GM/T0044-2016 SM9 标识密码算法》密码行业标准. 2020 年4 月, GB/T 38635.1-2020《信息安全技术SM9 标识密码算法第1 部分: 总则》、GB/T 38635.2-2020《信息安全技术SM9 标识密码算法第2 部分: 算法》两项国家标准获批发布, SM9 正式成为国家标准, 将于2020 年11 月1 日起实施. SM9 相关算法已被陆续纳入ISO/IEC 国际标准, 相关研究取得了积极进展[20–25]. 然而, 目前未见基于SM9 的标识签密方案在国际密码学主流期刊和会议上正式发表, 现有标识签密方案依然以国外设计为主.
1.1 本文贡献
面向密码技术自主先进安全可控的战略需求, 本文根据SM9 标识密码算法的特点, 凝练其核心技术,利用非对称双线性对提出首个基于我国SM9 商用密码的标识签密方案. 方案具有定长的系统公钥、用户私钥和签密密文, 其中用户的私钥由一个群元素组成, 密文由两个群元素和n 比特组成, n 为签名数据的长度. 与先采用SM9 数字签名算法对数据进行签名, 然后利用SM9 加密算法加密签名后的数据相比, 本文方案的计算开销和密文长度明显减少. 在随机谕言模型中, 基于q-BDHI 困难问题假设, 证明方案在适应性选择密文攻击模型下是不可区分的. 基于q-SDH 困难问题假设, 证明方案在适应性选择消息和标识攻击模型下满足存在性不可伪造. 理论分析表明方案的通信开销和计算开销与现有高效标识签密方案相当. 最后, 对方案进行实验仿真, 签密时间约为18 毫秒, 在实际应用中是可行的.
1.2 相关工作
本节回顾标识签密和SM9 标识密码算法的研究进展. 自2001 年Boneh 和Franklin 在文献[3] 中利用基于椭圆曲线的双线性对技术提出第一个实用可证明安全的标识加密方案后, 标识密码得到飞跃式发展. Malone-Lee 在文献[12] 中首次将标识密码体制拓展到签密系统, 提出第一个标识签密方案. Libert和Quisquater 在文献[26] 中指出Malone-Lee 方案的设计采用先加密后签名的方法, 无法达到语义安全(Semantic Security), 攻击者很容易区分挑战密文中的加密数据, 并提出一个更安全、更高效的标识签密方案. 2005 年, Barreto 等[27]提出一个在计算效率上优于之前所有签密方案的标识签密方案, 并在随机谕言模型中证明方案具有IND-CCA(Indistinguishability against Adaptive Chosen-Ciphertext Attasks)的安全性. 在给定标识和选择消息攻击下(Selective Identity and Chosen-Message Attacks, sID-CMA)满足存在性不可伪造.
Yu 等[13]借鉴Waters 标识加密方案[7]中的构造技术, 提出了第一个在标准模型下可证明安全的标识签密方案. 签名的安全性和密文的安全性分别基于CDH 和DBDH 困难问题假设. 然而, 文献[14] 指出Yu 等提出的方案存在和Malone-Lee 方案同样的安全缺陷, 无法达到语义安全, 并对Yu 的方案进行改进, 在保证不可伪造安全性的同时实现语义安全. Selvi 等[15]结合Waters 标识加密方案[7]和Paterson等人的标识签名方案[28], 设计一个在标准模型下可证明安全的标识签密方案. 该方案在选择消息和标识攻击下具有强不可伪造的安全性(Strong Unforgeability against Chosen Message and Identity Attacks,SUF-CMIA). Li 和Takagi[16]提出一个在标准模型下完全安全的标识签密方案, 代价是增加签密密文长度和计算开销. Li 等[17]对文献[13] 中的方案进行修改, 实现安全高效的标识签密方案. Karati 等[18]针对物联网应用需求, 提出一个适用于物联网的可证明安全的标识签密方案. 方案的安全性基于修改的BDHI 困难问题假设和修改的B-SDH(Bilinear Strong Diffie-Hellman) 困难问题假设. 文献[29–34] 分别研究了不同功能的签密方案.
自2016 年正式公布SM9 标识密码算法成为国家密码行业标准后, SM9 标识密码算法得到国内学者的积极研究. Cheng[35]给出了SM9 密钥协商协议和加密算法的规范安全性证明. 文献[21] 把盲签名技术拓展到SM9 数字签名算法中, 提出了一个基于SM9 的盲签名方案. 文献[20] 研究如何提高SM9 数字签名算法的计算效率, 提出能够实现快速签名和验证的具体方法, 有效降低了签名算法的计算复杂度. 文献[24] 研究SM9 标识密码算法中用户私钥的生成, 提出可分离匿名分布式密钥产生分发方案. 用户私钥生成是一个交互过程, 该过程无双线性对运算且不需要通过安全信道发送私钥. 文献[22] 提出基于SM9算法的可证明安全区块链隐私防护方案, 实现不可伪造、保证节点匿名和前向安全等性能. 文献[25] 研究SM9 标识加密算法中用户的撤销, 提出具有鲁棒性的安全用户撤销方案. 方案中用户的撤销通过服务器辅助实现. 文献[23] 研究了SM9 中R-ate 双线性对的快速计算方法. 综上, 目前尚未发现基于商密SM9 的标识签密方案的公开研究成果.
1.3 本文组织结构
在第2 节回顾双线性群、困难问题假设、标识签密和安全模型的形式化定义等预备知识. 第3 节给出基于SM9 的签密方案的具体构造. 在第4 节, 根据安全模型证明了方案的安全性, 并在第5 节对提出的方案进行性能分析和编程实验仿真. 第6 节对本文的工作进行总结.
2 预备知识
本节回顾双线性群、困难问题假设、标识签密和安全模型等基本知识.
2.1 双线性群
设λ 为安全参数, N 是与λ 相关的大素数. G1, G2和GT都是阶为N 的循环群, 双线性映射e:G1×G2→GT满足以下条件:
(1) 双线性性(Bilinearity): 对任意的元素P ∈G1, Q ∈G2和a, b ∈ZN, 都有e(aP,bQ) =e(P,Q)ab;
(2) 非退化性(Non-degeneracy): 至少存在元素P ∈G1, Q ∈G2, 满足e(P,Q)̸=1;
(3) 可计算性(Computability): 对于任意的P ∈G1, Q ∈G2, 存在多项式时间算法高效地计算e(P,Q).
此外, 若P, Q 分别为群G1和G2的生成元, 则存在有效的公开可计算同构映射ψ :G2→G1, 使得ψ(Q)=P. 双线性群BP 由以上五元组(G1,G2,GT,e,N) 组成.
2.2 困难问题假设

2.3 标识签密方案的定义
一个标识签密(Identity-Based Signcryption) 方案由以下四个多项式时间算法描述.
• Setup(λ): 以系统安全参数λ 为输入,系统建立算法Setup 输出系统主公钥mpk 和主私钥msk.该算法由密钥生成中心(KGC) 运行.
• KeyGen(mpk,msk,ID): 以系统主公钥mpk, 系统主私钥msk 和用户标识ID 为输入, 用户私钥生成算法KeyGen 输出用户ID 对应的私钥skID. 该算法由KGC 运行.
• Signcrypt(mpk,M,skIDS,IDR): 以系统主公钥mpk, 明文数据M, 签名加密者的私钥skIDS和接收者标识IDR为输入, 签密算法Signcrypt 输出签密密文CT. 该算法由签名加密者执行. 在下文中, 默认签名加密者和密文发送者是同一个实体.
• Unsigncrypt(mpk,CT,IDS,skIDR): 以系统主公钥mpk,签密密文CT,发送者标识IDS以及接收者IDR对应的私钥skIDR为输入, 解密验证算法Unsigncrypt 输出明文数据-签名对(M,σ)或者⊥. 符号⊥表示该签密密文的解密结果不是一个由发送者签名的数据. 该算法由密文解密者执行.
标识签密方案的正确性要求对任意的(mpk,msk)←−Setup(λ), skID←−KeyGen(mpk,msk,ID)和 CT ←− Signcrypt(mpk,M,skIDS,IDR), 当且仅当发送者 IDS对 M 进行了有效签名,Unsigncrypt(mpk,CT,IDS,skIDR)=(M,σ).
2.4 安全模型
签密既包含数据加密功能, 又包含数据签名功能. 只有授权的接收者才能正确解密获得明文数据, 并验证发送者是否对该数据进行签名. 因此, 签密的安全性不仅要求保护数据的私密性, 而且要求加密数据签名的不可伪造性. 本文参考文献[27], 针对数据私密性, 给出在适应性选择密文攻击下的不可区分性(Indistinguishbility against Adaptive Chosen-Ciphertext Attacks, IND-CCA) 安全模型; 针对签名的不可伪造性, 给出适应性选择消息和标识攻击下的存在性不可伪造(Existentially Unforgeable against Adaptive Chosen Message and Identity Attacks, EUF-CMIA) 安全模型. 这两个安全模型都是通过由挑战者(challenger) 和攻击者(adversary) 参与的游戏来定义. IND-CCA 安全模型的定义如下.
系统建立阶段. 给定安全参数λ, 挑战者运行算法Setup(λ), 生成主公钥mpk, 并发送mpk 给攻击者.
询问阶段1. 攻击者可以适应性询问以下谕言器.

猜测阶段. 最后, 攻击者输出对µ 的猜测µ′∈{0,1}. 如果µ′=µ, 则攻击者获胜.
定义攻击者A 获胜的优势为

EUF-CMIA 的安全模型定义如下.
系统建立阶段. 给定安全参数λ, 挑战者运行算法Setup(λ), 生成主公钥mpk, 并发送mpk 给攻击者.
询问阶段. 攻击者可适应性发起IND-CCA 安全模型中的询问, 挑战者按IND-CCA 安全模型回复攻击者.

3 方案构造
本节给出基于SM9 的标识签密方案的具体构造. 方案设计采用SM9 标识密码算法中的符号, 方案的具体描述如下.
3.1 方案描述

3.2 方案正确性分析
假设签密密文CT=(c,S,T) 由发送者IDS生成, 接收者为IDR, 则:

本文方案满足标识基签密系统的正确性要求.
4 安全性分析
本节分析上述方案的安全性. 从方案的构造可以看出,当系统的主公钥确定后,hid 和N 是固定的. 为描述方便, H1(ID||hid,N) 和H2(M||w,N) 分别简写为H1(ID) 和H2(M||w). 方案的安全性由定理1和定理2保证. 安全性证明借鉴文献[27] 中的证明技术.
定理1 令密码杂凑函数H1,H2,H3是随机谕言器. 如果q-BDHI 问题是难解的, 则本文提出的基于SM9 的标识签密方案是IND-CCA 安全的.

• H3询问. 针对三元组(Ti,wi,IDi) 的询问, B 为H3建立列表L3, 列表中的元素以四元组(T,w,ID,R) 的形式存储. 如果(Ti,wi,IDi) 在L3中, 则返回相应的Ri. 如果不存在, 从{0,1}n中随机选取一个元素Ri, 设H3(Ti,wi,IDi)=Ri, 发送Ri给A 并以(Ti,wi,IDi,Ri) 更新L3.
询问阶段1.

其中等式(4)中的左边是可计算的.
接着, B 执行以下步骤:
S1 遍历列表L3, 找出所有满足Ti=T,IDi=IDv的四元组(Ti,wi,IDi,Ri). 若没有对应的四元组, 则拒绝该密文并结束, 否则执行步骤S2;
S2 计算Mi=c ⊕Ri, 遍历列表L2, 找到(Mi,wi) 相应的hi, 如果不存在, 则拒绝该密文并结束,否则执行步骤S3;
挑战阶段. A 输出两个等长的挑战明文数据(M0,M1) 和发送者/接收者组合(IDS∗,IDR∗), 其中A没有询问过IDR∗的私钥. 如果IDR∗̸= IDk, B 终止模拟. 否则, B 随机选取t ∈Z∗N, c∗∈{0,1}n,S∗∈G1, 计算T∗=−tP1, 并返回挑战密文CT∗=(c∗,S∗,T∗). 设r∗=t/a, 因为α=−a −Ik, 有
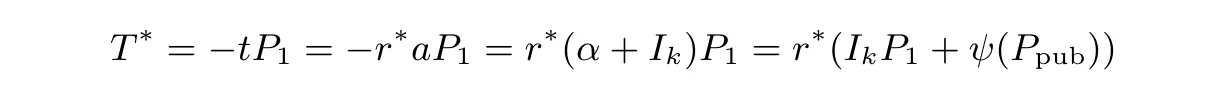
因此, A 不能分辨CT∗是否是一个有效的签密密文, 即模拟和真正的方案攻击不可区分, 除非它询问过H2或者H3关于w∗=e(P1,Ppub)r∗的值.
询问阶段2. A 继续询问私钥, 签密密文和解密. 但是, A 不能询问IDR∗的私钥, 同时也不能询问CT∗对应(IDS∗,IDR∗) 的解密. B 根据询问阶段1 回复A.

因此, 可计算q-BDHI 问题的解为
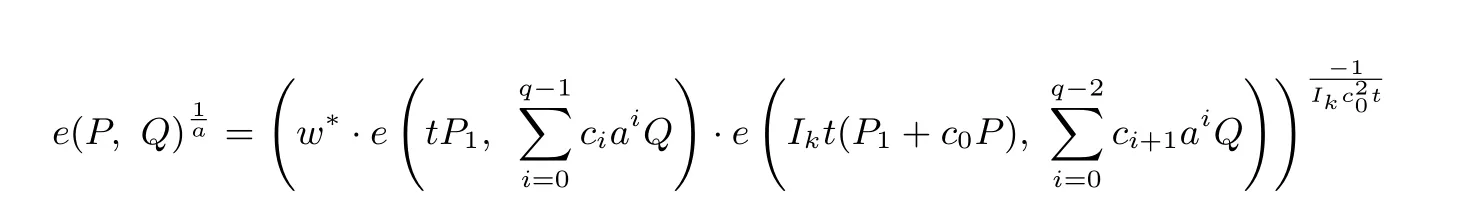
最后分析解决q-BDHI 问题的概率. 从证明的设置可知, I= IDk, 即A 选择IDk作为挑战接收者的概率为1/qH1. 综上, 如果A 以不可以忽略的优势ϵ 攻破所提的方案, 则B 解决q-BDHI 问题的概率为
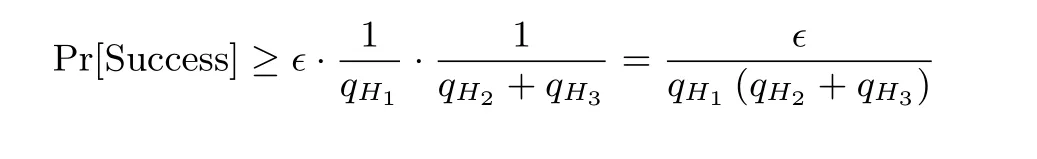
定理2 令密码杂凑函数H1,H2,H3是随机谕言器. 如果q-SDH 问题是难解的, 则本文提出的SM9标识签密方案是EUF-CMIA 安全的.

• H3询问. 针对三元组(Ti,wi,IDi)的询问,B 为H3建立列表L3,列表元素以四元组(T,w,ID,R)的形式存储. 如果(Ti,wi,IDi) 在L3中, 则返回相应的Ri. 如果不存在, 从{0,1}n中随机选取一个元素Ri, 设H3(Ti,wi,IDi)=Ri, 发送Ri给A 并以(Ti,wi,IDi,Ri) 更新L3.
效果分为显效、有效以及无效3个等级,显效是指患者治疗后的临床症状明显改善,透析过程中无低血压发生;有效是指患者的临床症状有所缓解,收缩压在透析的过程中基本正常;无效则为患者在治疗的过程中临床症状和体征无明显好转,并出现低血压[5]。
询问阶段.

其中等式(8)中的左边是可计算的.
接着, B 执行以下步骤:
S1 遍历列表L3, 找出所有满足Ti= T,IDi= IDv的四元组(Ti,wi,IDi,Ri). 若没有对应的四元组, 则拒绝该密文并结束, 否则执行步骤S2;
S2 计算Mi= c ⊕Ri, 遍历列表L2, 找到(Mi,wi) 相应的hi, 如果不存在, 则拒绝该密文并结束, 否则执行步骤S3;
S3 检查所找到的hi是否满足等式(8), 如果都不满足, 则拒绝该密文并结束. 如果存在唯一满足条件的三元组(Mi,wi,hi), 则输出Mi和签名(hi,S) 作为解密结果发送给A.

5 方案性能分析
本节从存储效率、安全性、困难问题假设和计算效率等方面分析基于SM9 的签密方案.
5.1 理论分析
首先从理论上比较本方案和相关的标识签密方案, 对比结果见表1 和表2. 从表1 可知文献[18] 和本方案具有定长的公钥且安全性都基于q-type 类型的困难问题假设, 其他方案的公钥长度是线性的, 安全性基于DBDH 和CDH 困难问题假设. 本方案的安全性依赖于随机谕言模型, 其他方案都在标准模型下证明方案的安全性, 但文献[13,14,16,17] 存在安全性不足. |G1|, |G2| 和|GT| 分别表示群G1, G2和GT中元素的大小, n 是消息的比特长度, ROM 表示随机谕言模型, |G| 表示对称双线性对中群G 元素的大小(比较方案的设计都基于对称双线性对), N 为大素数且是群G, G1, G2和GT的阶, k 是相应文献方案中与哈希函数输出长度和标识长度相关的整数. 其中“*” 表示对应的安全性存疑.
从表2 可知, 本方案的计算效率和比较方案总体相当, 其中解密验证算法的效率与文献[18] 是可比的,仅包含两个双线性对运算, 优于文献[13–17] 中的方案. 对比方案都基于双线性群设计且方案的构造都使用了密码哈希函数, 而生成双线性群的操作可以预先完成, 所以本文忽略这部分的计算开销. 由于比较文献中使用的密码哈希函数类型较多, 本文统一定义HB为映射到比特串的密码哈希函数, HZ为映射到的密码哈希函数, N 为大素数且是相应方案中群的阶. 计算效率的对比结果见表2.

表1 标识签密方案性能比较Table 1 Performance comparison of identity-based signcryption schemes

表2 标识签密方案计算效率比较Table 2 Computation comparison of identity-based signcryption schemes
由于比较方案的设计采用乘法群表示, 本文使用加法群表示. 为方便比较, 本文统一在加法群下统计计算开销并定义如下符号: sm1表示群G1中的标量乘运算(Scalar Multiplication)1在乘法群表示中, 该运算等价于相应群中的指数运算., sm2表示群G2中的标量乘运算, p 表示双线性对运算, Et 表示群GT中的指数运算, sm 表示对称群G 中的标量乘运算.表2 的统计不包含中的模运算(Modular), G, G1和G2中的点加运算(Point Addition), GT中的乘法运算.
5.2 实验仿真
本节对方案进行编程仿真, 测试方案中各个算法的运行时间. 为测试方便, 忽略方案描述中ψ 函数,并使用Type III 双线性对仿真方案. 仿真中使用的库为PBC (Pairing-Based Cryptography), 采用的椭圆曲线为Type F, 其中|G1| = 256 bits. 测试环境中所用的设备是一台内存为16.0 GB 的笔记本电脑,操作系统为64 位的Windows 10, CPU 为Intel(R) Core(TM) i7-8558U@1.80Hz 2.00 GHz, 使用的编程语言为C++. 本文运行程序20 次后取平均值, 测试的结果如图1 所示. 从图1 可知, 本方案的签密算法时间约为14.65 毫秒, 具有一定的可行性. 系统建立和解密验证开销较大, 系统建立时间约为54.4 毫秒, 主要开销源自群元素的初始化和双线性对运算及群G2上的标量乘法. 解密和验证算法计算时间约为86.5毫秒, 主要开销源自两个双线性对运算, 群G2上的标量乘法, 群GT上的指数运算和三个密码哈希函数的计算.

图1 方案算法的运行时间Figure 1 Computational overheads for each algorithm
6 总结
本文秉承核心技术自主创新、信息安全自主可控的理念, 结合我国商用密码SM9 标识密码算法, 设计了首个基于SM9 的高效标识签密方案, 同时实现数字签名和数据加密的功能, 有效保护了签名数据的私密性. 与先采用SM9 签名算法对数据签名, 然后用SM9 加密算法加密签名后数据的方法相比, 本方案能够显著减少计算开销和通信开销. 在随机谕言模型中, 证明方案是IND-CCA 和EUF-CMIA 安全的.方案的安全性依赖于q-BDHI 和q-SDH 困难问题假设. 理论分析和实验仿真结果表明本文提出的基于SM9 的标识签密方案与现有国际主流高效标识签密方案在计算效率和通信效率上相当, 在实际应用中是可行的.
