一种高效的关于两方集合并/交集基数的隐私计算方法
2021-05-15赵运磊
程 楠, 赵运磊
1. 复旦大学 软件学院, 上海210203
2. 复旦大学 计算机科学技术学院, 上海210203
1 引言
在当今的数字时代, 越来越多的公司通过收集数据, 并基于自身的合理需求加以利用而获得了相当的回报, 例如: 基于消费者使用偏好等数据, 互联网公司研发出推荐系统, 个性化地提供互联网产品或服务;基于用户历史浏览数据并结合智能算法, 广告商实现了精准营销. 这一回报也就反过来激发出更多的数据采集需求, 在这个过程中, 用户的个人隐私必然越来越难以被保护, 因此数据隐私计算技术就变得越来越重要: 于用户而言, 这一技术能在最大限度地保护他们的隐私的同时提供便捷; 于商家而言, 这一技术可以在帮助他们避免核心数据的泄漏的前提下最大限度地发挥其核心数据的价值. 在全球日益重视数据安全的背景下, 各大国家已纷纷立法保护数据隐私(如美国的HIPAA、COPPA、GLBA、欧盟的DPP), 数据隐私计算技术逐渐成为当前学界研究的一个热潮.
两方PSI (Private Set Intersection) 问题是关于安全两方计算模型中最基础的一类问题. 在两方PSI问题中, 我们用Alice 和Bob 表示参与方, 并假设其分别持有任意长度字符集合X 和Y. 在一系列的交互完成后, 我们要求至少有一方能得到双方的交集X ∩Y, 并且每一参与方都不能获知关于对方集合元素的任何其它知识. 我们可以使用基于不经意传输(Oblivious Transfer, OT) 的协议[1–4]来高效地解决这个问题.
两方PSU/PSI-CA (Private Set Union/Private Set Intersection Cardinality) 问题是两方PSI 问题的延伸, 它要求最终计算出|X ∪Y|/|X ∩Y|, 且在此过程中不泄漏任何其它的信息(包括自己的任何一个元素信息及自己的集合大小). 该问题对应于现实中许多隐私计算场景, 例如: 在社交网络中, 两个用户可以在不泄漏自己具体好友信息的情况下比较其相同好友的比例, 来计算社交关系重合度; 在健康领域, 持有私有基因数据的客户可以放心地与公共风险基因数据库交互, 从而得知自己感染某种疾病的概率; 本文就是要讨论解决PSU/PSI-CA 问题的相关协议.
一般而言, 理论上所有的隐私计算问题都可以用通用的的安全计算协议来解决(如GMW 协议[5]、混淆电路[6]). 但这些通用的方案需要较高的计算和通讯代价. 因而, 对于具体的安全计算问题, 我们通常使用专用的高效协议. 具体地, 对于解决PSU/PSI-CA 问题的协议而言, 从输出结果的精确程度来分类, 我们分为如下两类.
(1) 第一类协议为完美计算协议, 它输出精确的结果. 以文献[7–12] 等工作为例, 它使用模糊多项式评估方法, 选定一个多项式来代表输入集合并通过同态加密技术来合并评估集合的交. 但是这一类的协议使用大量的公钥原语, 因此, 即使在半诚实模型下, 它们实际执行时的资源消耗也非常大.
(2) 第二类协议为不完美计算协议, 它的输出结果容许一定的误差. 面对数量级较大的数据时, 该类协议由于能够在效率与可用性之间取得较好的平衡, 因而在现实中得到更广泛的应用. 例如:
• Egert-Fischlin 协议[13]通过将其中一方的布隆过滤器的每一位用ElGamal 公钥系统[14]进行加密, 从而实现隐私计算. Egert-Fischlin 协议的优点在于非平衡性, 协议的主要计算开销集中于其中一方, 因此它适合于服务器-客户端类型的应用场景[13]. 不过因其计算与通信复杂度均为O(n),所以当输入量级逐渐变大时, 它便难以推广应用.
• Dong-Loukides 协议[15]基于Flajolet-Martin 技术[16]和OT14技术, 它够将长度为n 的集合预处理为长度为log(n) 的Flajolet-Martin 概要[16], 因而大大降低了后续使用OT14原语产生的计算开销. 但该计算必须串行地调用OT14协议, 因此它的通信轮数较多, 网络环境较差时, 网络时延影响比较明显. 此外, 为了提高输出结果的精确度, 这一协议需要在离线阶段对同一个集合生成大量不同的Flajolet-Martin 概要[16], 因此它的哈希成本相对较高. 不过, 实验数据[15]表明,Dong-Loukides 协议依然是目前解决PSU/PSI-CA 问题最高效的协议之一.
本文侧重于不完美计算协议的设计与分析, 因为它能够在效率与可用性之间取得较好的平衡. 受Dong-Loukides 协议的启发, 我们提出一种基于预计算OT 模型[17]的方案, 在该方案中, 无论是解决PSU-CA 问题还是PSI-CA 问题, 首先都要进行秘密分享(Secret Sharing), 它分为两个阶段: 即离线阶段和在线处理阶段. 离线阶段中, Alice 和Bob 分别调用Silent-OT 协议[18]交互生成足够多的伪随机相关消息对. 在线阶段中, 假设Bob 为不经意传输的发送方, 则Bob 根据之前已生成好的伪随机相关消息对跟自己真正要发送的消息做掩码运算, 之后发送给Alice, Alice 直接通过离线阶段收到的消息进行解密.这两步操作完成后, Alice 和Bob 将分别得到关于HW(BFA∨BFB) 的秘密分享SA和SB. 而后:
• 在解决PSU-CA 问题的子协议中, 不妨设Alice 为最终结果的输出方, 那么此时Bob 需将其秘密分享SB发送给Alice, 则Alice 将两个秘密分享SA和SB合并, 最终输出估算的两个集合的并集的势.
• 在解决PSI-CA 问题的子协议中, Alice 和Bob 还需要额外执行一个同态计算协议, 完成协议执行后, 输出方输出估算的两个集合的交集的势.
由于进行秘密分享的离线过程的计算可以事先完成, 而在线阶段的计算只进行高效的掩码运算, 因此我们的秘密分享非常高效. 而且无论是对应PSU-CA 还是PSI-CA 问题的子协议, 后续的开销都很小. 因此同之前大部分基于公钥计算的协议相比, 我们的方案带来了较大的效率提升.
2 预备知识
在本文中, 对于一个有限集合X 我们用符号|X| 表示它的势, 符号|X|∗表示集合势的近似整数估值. 符号BFX表示对应集合X 的布隆过滤器. 表达式r ←$S 表示从有限集合S 中随机均匀选取一个元素r. 对于正实数x, 符号⌊x⌋表示x 向下取整的值. 对于二进制串B, 符号HW(B) 表示B 上1 的个数.
2.1 布隆过滤器
在我们的方案设计中, 我们首先使用布隆过滤器(Bloom Filter, BF) 对集合进行预处理, 布隆过滤器被Bloom[19]首次提出, 他将一个集合中的每一个元素通过若干哈希函数到映射到一个二进制串, 最终得到一个轻量级的二进制串, 这就是布隆过滤器. 它主要被用于检测一个元素是否隶属于某些数据集合. 当构建某个数据集X 的布隆过滤器时, 首先我们会选定生成参数: 包括k 个相互独立的哈希函数, 该布隆过滤器所预设的容量d, 错误率e. 此外初始化一个全为0 的二进制串BFX, 设其长度为m, 继而使用k个彼此独立的哈希函数hi: {0,1}{1,··· ,m} (其中i ∈{1,··· ,k}) 将集合中的每一个元素映射到某个正整数, 若BFX对应位置的值为0, 则将其更改为1. 任何第三方若要检测某个元素a 是否位于集合X中, 首先可使用对应的哈希函数组计算a 所有的映射值, 接着检查BFX上对应位置是否全为1, 是的话说明元素a 很可能位于集合X 中, 否则说明a 一定不是集合X 中的元素.
图1 展示了对集合{x,y,z} 生成布隆过滤器及进行元素检测的图示[20], 其中哈希函数组的个数为k =3, 最终生成的布隆过滤器长度m=18, 其中元素w 经过检测可知不在集合{x,y,z} 中, 因为该元素的某个哈希值对应的位置为0.
由于哈希碰撞的存在, 布隆过滤器存在一定的假阳性检测. 布隆过滤器的长度m 与哈希函数组的大小k 和其容量大小d 直接相关, 直观上, 将m 取得很大的话, 哈希的碰撞会减少, 布隆过滤器的检测错误率e 会降低, 但这样在计算上会降低效率. 根据文献[21], 使用如下公式对k 和m 进行约束, 我们可以在布隆过滤器的计算效率与错误率之间取得较好的平衡.

图1 布隆过滤器生成及元素检测示例Figure 1 Example for Bloom filter generating and membership checking

对于一个集合X, 我们可以用如下公式[22]估算它的势:
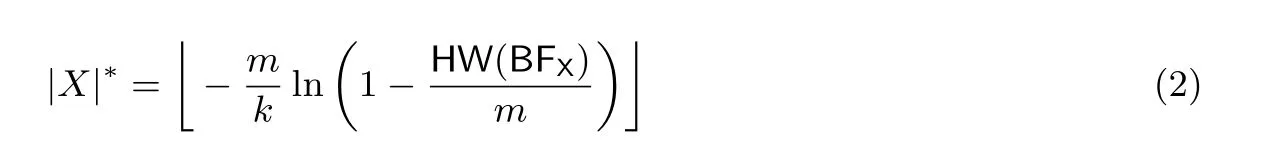
对两个不同的集合A 和B, 设其使用同样的参数分别生成BFA,BFB, 令BFA∨BFB表示BFA和BFB按位求或的二进制串, 则估算两个集合A, B 的并交集大小的公式分别为:

综上所述, 布隆过滤器可以被用来估算两方集合的并集的势, 不过这隐含地意味着它们都知晓对方集合的势的上界.
2.2 Paillier 加密系统
本文在解决PSI-CA 问题的协议中使用了Paillier 加密系统[23], 它是一个具有同态性质的公钥加密系统, 分为密钥生成算法、加密算法和解密算法, 如下所示(其中符号Z∗n表示集合, 它满足Z∗n= {x ∈Zn:gcd(x,n)=1}).
密钥生成算法:

Paillier 加密系统的安全性基于判定性复合剩余类假设(Decisional Composite Residuosity Assumptio, DCRA). 一般认为, 当n 足够大时, 对攻击者而言, 不知道n 的素因式分解, 判定性复合剩余问题是困难的. 该加密系统具备加法同态性:
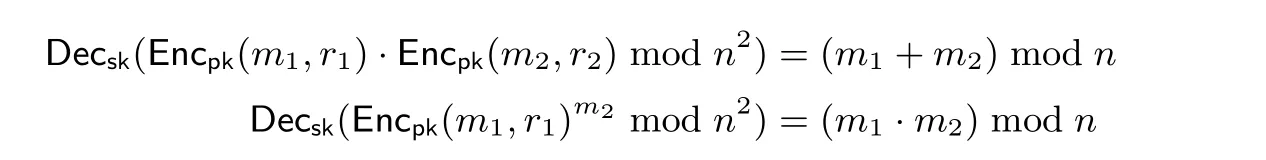
2.3 不经意传输


图2 离线-在线框架Figure 2 Offline-online framework
3 两方PSU/PSI-CA 协议
本节中, 我们将给出解决PSU-CA 问题和PSI-CA 问题的协议构造和相关证明. 首先, 我们分别给出解决PSU-CA 问题和PSI-CA 问题的两个协议构造(3.1 节), 然后分别给出它们的正确性证明(3.2 节),最后我们给出基于模拟的安全性证明(3.3 节).
3.1 协议构造
在两个协议执行中, 我们不妨设两方参与者分别为Alice 和Bob, 分别持有集合A 和B. 我们的协议要求两方输入两个结构相同的布隆过滤器, 其生成过程如下:
(1) Alice 和Bob 约定足够大的容量d, 输入错误率e, 由公式(1)并经过取整计算, 分别得到所使用哈希函数个数k 及所要生成的布隆过滤器的长度m.
(2) Alice 和Bob 分别使用相同的k 个哈希函数对他们的输入集合A,B 进行处理, 最终独立地得到各自的布隆过滤器BFA,BFB.
此后在协议描述中我们直接将BFA,BFB作为输入, 不再赘述该生成过程. 无论是PSU-CA 协议或者PSI-CA 协议, Alice 和Bob 在离线阶段执行相同的操作, 如下所示.
3.1.1 离线阶段

3.1.2 在线阶段
无论是计算PSU-CA 问题还是PSI-CA 问题, Alice 和Bob 首先都要执行秘密分享协议, 如图3 所示.

图3 秘密分享协议Figure 3 Secret sharing protocol
(i) 首先Alice 和Bob 执行两轮交互, 具体步骤如下:


图4 同态计算协议Figure 4 Homomorphic computing protocol
3.2 正确性分析


故原命题得证.
3.3 安全性分析
目前两大主流安全模型是半诚实模型(Semi-Honest Model) 和恶意模型(Malicious Model)[27]. 在半诚实模型下, 敌手会记录协议交互过程中的所有数据, 并尝试提取其它参与方的秘密信息. 在恶意模型下, 敌手会以任意的方式偏离协议的执行来进行破坏或窥探.
本文所涉及的所有安全协议都是在半诚实模型下[27]证明的. 一般而言, 当构建一个隐私计算协议时,我们会首先在半诚实模型下构建. 虽然半诚实模型比恶意模型的假设要弱, 但实际上, 现实的业务部署都必须符合某些安全法令的制约, 这保证了半诚实模型下的协议依然有广泛的应用前景.

定理1 存在一个概率多项式时间的模拟器Sim1使得对于所有的安全参数n 满足2n> |BFA| 和输入BFA, 有其中S(·),R(·) 分别表示Alice 和Bob 的伪随机相关预设消息,(BFA,BFB,S(·),R(·)) 表示在协议#1 执行中Alice 的视图.

算法1: Alice 的模拟算法Input: 1n,BFA,{(R01,R11),··· ,(R0m,R1m)}Output: Sim1(·)1 随机选取¨r ←${0,1}m, 作为Bob 第一轮发送给Alice 的输入模拟.2 Alice 真实按照协议执行计算{(M0i,M1i)}i∈[m] 和S1, 模拟第二轮的输出.
证明: 我们用算法1 描述Sim1(·).
在算法1 的第一步中, ¨r 在 {0,1}m上随机均匀选取, 而在真实的执行中, ¨r = {d1⊕(1 −BFB[1]),··· ,dm⊕(1 −BFB[m])}, 因为di为随机选取, 因此模拟的Bob 输入¨r 与真实协议执行中Bob发送给Alice 的¨r 是计算不可区分的. 在第二步中, 由于上述模拟算法完全按照真实协议执行的步骤, 因此模拟的输出与真实的输出同分布.
综上所述, 上述Alice 的模拟算法能模拟协议#1 执行中Alice 的交互视图. 因此定理得证.
定理2 存在一个概率多项式时间的模拟器Sim2使得对于所有的安全参数n 满足2n> |BFA| 和输入BFA,BFB, 有

其中S(·),R(·) 分别为Alice 和Bob 的伪随机相关预设消息, View#1
B (BFA,BFB,S(·),R(·)) 为上述协议
#1 中Bob 的交互视图.

算法2: Bob 的模拟算法Input: 1n,BFB,HW(BFA ∨BFB),R(·)Output: Sim2(·)1 Bob 输入R(·) 和BFB 之后, 按照协议#1 的真实执行过程输出Bob 第一轮的输出模拟¨r.2 对于∀i ∈[m], 选取ri ←${0,1}n. 选取MBFB[i]i = ri ⊕Rdii . 计算S1 = (2n +m −HW(BFA ∨BFB)−(∑m i=1 ri) mod 2n)) mod 2n. 则上述{(M0i,M1 i)}i∈[m],S1 即为对第i ←${0,1}n;令M1−BFB[i]二轮Alice 输入的模拟.3 真实地按照第三轮的执行计算S2 作为对S2 的模拟输出.

定理3 存在一个概率多项式时间的模拟器Sim1使得对于所有的安全参数λ 满足2λ>m 和所有的输入(S(·),R(·),|A|,|B|,m,k,(pk,sk)), 有


算法3: Alice 的模拟算法Input: 1λ,S(·),|A|,f(·)Output: Sim1(·)1 令S∗1 := Encpk(0), 模拟Alice 第一轮输出S1 的模拟.2 令ˆS∗:= Encpk(0), 作为第二轮中ˆS 的模拟输出.3 随机选取β ←$(0,1) (表示从该区间选取小数点后四位的小数), 计算ϕ = |A|−f(·)+β, 然后计算Dec ˆS∗= p·m ϕ·k exp m, 模拟Bob 的ˆS 的解密值T∗, 最后输出f(·).


算法4: Bob 的模拟算法Input: 1λ,R(·),|B|,BFB Output: Sim2(·)1 令 ˆS1∗:= Encpk(0), 模拟协议第一轮Alice 的输入 ˆS1 的模拟.2 令ˆS∗:= Encpk(0), 作为第二轮ˆS 的模拟输出.
证明: 我们用算法4 描述Sim2. 由于Bob 只需要模拟由同态加密保护的消息, 由于Paillier 加密系统抗选择明文攻击(Chosen Plaintext Attack, CPA) 的特性, 因此其能够完美模拟真实协议中的消息. 那么通过上述给定输入1λ,R(·),|B|,BFB, 该构造能够模拟协议#2 中Bob 的交互视图, 故定理得证.
综上所述, 结合定理1 和定理2, 我们使用模拟的方式证明了协议#1 在半诚实模型下的安全性. 结合定理1–4, 我们证明了协议#2, 即解决PSI-CA 问题的协议在半诚实模型下也是安全的.
4 性能评估
本节我们从理论分析和具体实验两个方面, 将我们的协议同Dong-Loukides 协议[15]在不同指标上进行比较, 来说明我们的协议在总体上有较好的性能, 并且适用于更广泛的应用场景.
4.1 理论评估
表1 为定性的性能对比. 其中N 为集合的大小, k1为生成布隆过滤器的哈希函数个数, k2为生成Flajolet-Matin 概要所需的哈希函数个数. 且k1≪k2. 其中的哈希开销一列是指预处理阶段的哈希开销,在Dong-Loukides 协议中即指将集合转化为Flajolet-Martin 概要[16]的哈希开销(为了提高协议的计算结果准确度, 一般需要将k2设置为比较大的常数), 而在协议#1,#2 中, 指布隆过滤器生成时的哈希开销(此时k1=−, r 为错误率).
从表1 可以看出协议#1 和协议#2 的通信轮数及幂指数运算开销均为为常数, 此外可知, 协议#1和协议#2 除了通信量比Dong-Loukides 协议要大之外, 其它方面都更好. 且当一个数据集的数据有微小更新时, 在Dong-Loukides 协议中也需要几乎重新生成Flajolet-Matin 概要, 这一不足也大大限制了Dong-Loukides 协议可能适用的应用场景. 此外, Dong-Loukides 协议的离线预计算依赖于具体的数据集,而我们所调用的Silent-OT 协议[18]不依赖于任何具体的数据集, 因此它具有更广的应用场景.

表1 理论对比Table 1 Theoretical comparison
4.2 实验评估
我们分别对三个协议做了实现(https://github.com/athenKing/PSU-PSI-CA) 来对比他们具体的性能表现, 三个协议都通过C++ 完成实现, 进行测试的平台搭载了2.9 GHz double core Intel-core I5 处理器和16 GB 1867 MHz DDR3 内存. 该测试在LAN 网络环境下完成, 网络时延较低. 在Dong-Loukides协议的实现中, 设置安全参数λ = 128, 设置独立哈希函数的个数k2为4096, 输出的Flajolet-Martin 概要[16]长度设置为32 (其理论上能统计至多232−1 个元素). 协议#1 和协议#2 的实现中, 同样设置安全参数λ=128, 布隆过滤器的错误率设为r =0.05, 三组数据(从小到大) 对应的布隆过滤器最大容量分别设为5000, 50 000, 400 000. 表2 展示了它们在不同数量级输入下的实际性能比较结果. 其中Nx和Ny表示输入的两个集合的大小, PSU/PSI-CA 误差(%) 表示输出结果的相对误差, 即两个集合并集和交集基数输出结果相对真实结果的误差. DL 协议表示Dong-Loukides 协议.

表2 实验对比Table 2 Experimental comparision
由表2 的实验结果可知, Dong-Loukides 协议的预处理阶段比较耗时, 因此它不适合数据集更新频繁的场景, 只适用于某些数据永久或半永久化存储场景下的安全计算. 可以看到, 无论数据集的大小, 相比Dong-Loukides 协议协议#1 和协议#2 的总耗时都更小, 而且当数据集的输入从小变大时, 这种性能优势也越来越明显. 所以, 我们的协议在数据集更新频繁的计算场景中有比Dong-Loukides 协议更高的计算效率.
5 总结与展望
本文提出一种新的解决PSU/PSI-CA 问题的不完美计算协议, 并在半诚实模型下证明了它的安全性.它使用布隆过滤器对集合预处理, 并混合了OT 预处理[17]和Paillier 同态加密技术[23]. 同最先进的协议之一Dong-Loukides 协议相比, 该协议总耗时更低, 并且有较广泛的应用场景.
我们的协议不能抵抗恶意的敌手, 因此下一步, 通过结合当前方案和零知识证明[27]的技巧, 我们会尝试构建一个高效的在恶意模型下[27]可证明安全的协议.
