基于初值更新的水下纯方位短时目标跟踪

郑 艺, 王明洲

基于初值更新的水下纯方位短时目标跟踪

郑 艺, 王明洲

(中国船舶集团有限公司 第705研究所, 陕西 西安, 710077)

水下被动单站纯方位目标跟踪具有布局简单、隐蔽性强的优点, 但所使用的滤波方法均存在对初值选取敏感的问题, 且实际工程中会遇到目标速度快、观测时间短、量测数据少的情况, 使这一问题更加凸显。针对这一情况, 文中研究了初值对滤波产生影响的原因和方式, 提出了一种基于初值更新的扩展卡尔曼滤波改进方法, 通过后向迭代对初值重新估计并不断更新, 逐步降低初值误差对滤波结果的影响。仿真结果表明, 该方法可减少滤波器对初值选取的依赖, 降低最终的估计误差。

纯方位; 目标跟踪; 初值; 后向迭代

0 引言

水下纯方位目标跟踪是仅通过观测到的目标方位信息来估计目标的位置、速度等状态的过程, 由于其可以在隐蔽自身的情况下对目标进行跟踪, 更适合进行秘密的行动策划和目标打击, 是目标跟踪领域的重要方法之一。其中, 单观测站纯方位目标跟踪是指仅依靠单个观测站获得的目标方位信息来进行目标跟踪的方法, 具有成本低、布局简单、隐蔽性强等优点。但单站纯方位目标跟踪的难点更为突出, 主要是由于观测过程是非线性的[1], 且目标距离的可观测性不确定。针对观测过程非线性这一问题, 目前应用最广泛的是非线性高斯贝叶斯滤波器方法, 主要有扩展卡尔曼滤波(extended Kalman filter, EKF)[2]、无迹卡尔曼滤波(unscented Kalman filter, UKF)[3]以及粒子滤波[4](particle filter, PF)等方法。寻求收敛速度快、稳定性好的滤波跟踪算法是研究的重点。近年来, 学者们致力于纯方位目标跟踪方法的研究, 如基于正交三角分解的平方根无迹卡尔曼滤波(square root unscented Kalman filter, SRUKF)方法[5]、自适应方差的容积卡尔曼滤波(cubature Kalman filter, CKF)方法[6]、基于平滑器的滤波方法[7-8], 以及不等式约束下的滤波方法[9]等在该领域的研究。

上述滤波方法存在一个共同的问题, 就是对于滤波初值的选取非常敏感, 并且滤波初值带来的误差可能在多次迭代后依然存在[10]。在实际工程应用中, 当被跟踪的目标为水下高速运动平台时, 末程攻击阶段会出现目标运动速度快的情况, 导致观测时间短。此时一般的非线性滤波方法难以迅速收敛, 初值选取带来的误差难以通过短时滤波得到消除, 初值对于滤波结果的影响更加不容忽视。针对卡尔曼滤波初值选取的问题, 主要有以下几种处理方法: 一是假定初值已知或不对初值选取方法作出讨论; 二是将关注点放在算法的收敛性上, 以此忽略初值误差带来的影响; 三是通过如最小二乘法、粒子滤波等方法对初值进行估计, 从而改善滤波性能。有学者也对此问题提出了一些改进方法: 李绍荣等[11]将测向交叉定位中的滤波初值分为2类, 从几何原理上解释了不同初值对定位结果的影响, 并提出了一种增加相位差观测量来改善定位结果对初值依赖性的方法, 但该方法需要已知来波频率, 对于水下被动跟踪而言实现; 余小琴等[12]提出了一种卡尔曼滤波初值选取方法, 但该方法需要多基地浮标进行几何定位解算, 对于单观测站并不适用。

针对水下高速目标运动速度快、观测时间短的问题, 文中以卡尔曼滤波为基础, 研究了滤波初值对目标状态估计结果产生影响的方式, 并针对这种现象提出了一种基于初值更新的EKF改进方法, 通过滤波后向迭代对初值进行不断更新, 从而减少对滤波初值的依赖, 降低跟踪误差。

1 初值选取的影响

1.1 基于EKF的单站纯方位目标跟踪

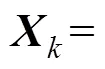
系统状态方程

系统量测方程

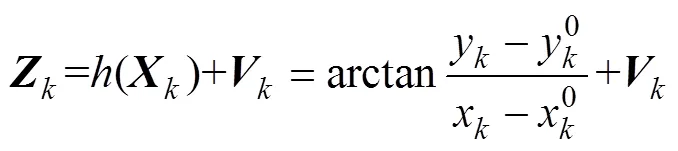
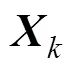
则线性化的量测方程可写为

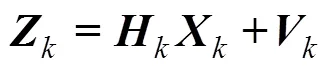
利用式(1)和式(4)组合成状态空间模型, 可利用EKF的递推方程进行状态估计, 完成目标跟踪, 步骤如下。

目标状态预测

状态协方差预测

卡尔曼滤波增益

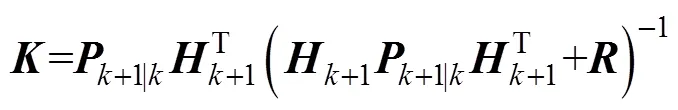
目标状态更新

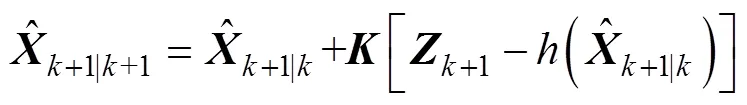
状态协方差更新

1.2 初值选取对定位结果的影响

对于NCV目标和匀速直线运动观测站, 可将目标作为静止参考点, 将观测站的运动轨迹转换为其对于目标参考点的相对运动, 因此, 文中以静止目标为例来说明初值的影响。

由图1可知, 对于纯方位单站被动目标跟踪而言, 由于目标位置的状态初值并不是随着迭代直接向真实值移动, 而是垂直于测向线方向移动。因此, 选取2种不同的初值0观察其递推情况, 如图2所示。每次迭代目标位置的状态估值都向垂直于此时刻的测向线方向移动, 经过3次迭代后, 位置估计结果位于点3处。由图可知, 此时图2(b)中的估计值已经非常接近真实值, 而图2(a)中的估计值向真实值的移动情况则不甚理想, 滤波结果呈现出对初值的依赖。实际工程中, 短时间内观测站难以通过足够的机动来使估值快速收敛, 且无法预知初值与真实值间的位置关系和误差, 因此初值对滤波误差的影响更为明显。

图1 目标位置估计值变化(情况1)

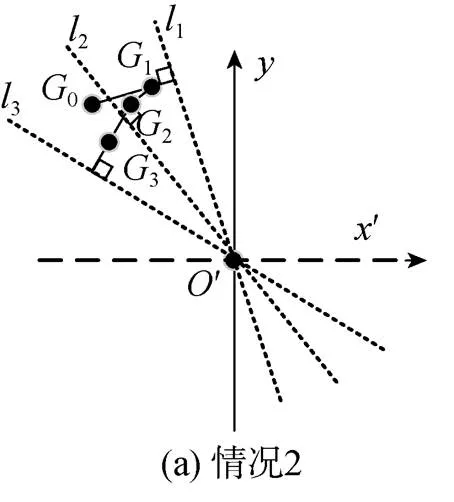
图2 不同初值滤波情况几何解释

通过仿真试验来观察单站纯方位目标估计中不同初值的滤波情况。设目标真实位置在原点处, 图3(a)初值坐标为(–10,10), 对应图2(a)中的情况2; 图3(b)初值坐标为(10,10), 对应图2(b)中的情况3。观测站从(0, –100)位置开始, 以50 kn的速度向45°方向行驶。经过60次观测, 通过常规EKF进行状态估计, 目标位置的估计分别如图3(a)、(b)所示, 并将状态估计变化部分进行放大显示。可以看到, 图3的仿真情形与图2的分析结果十分相似。

由此可见, 初值选取对于EKF的单站纯方位目标跟踪有重要影响。而对于观测时间较短的高速目标跟踪而言, 较少的滤波迭代次数和有限的观测站机动难以消除初值带来的误差, 初值选取不当对滤波结果的影响会更为显著。

2 基于初值更新的EKF改进方法

针对纯方位目标跟踪对初值选取的依赖性问题, 根据1.2节中所分析的初值对滤波的影响方式, 文中提出一种基于初值更新的EKF改进方法。该方法通过后向迭代滤波对初值进行估计和更新, 利用更新后的初值进行最新的目标状态估计, 以减少滤波对初值的依赖。

将式(1)展开为

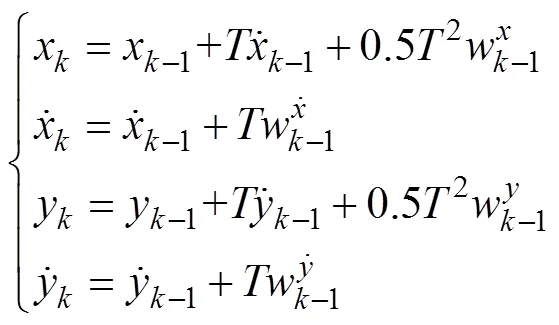
对于NCV目标, 有

将式(11)代入式(10)中, 整理可得

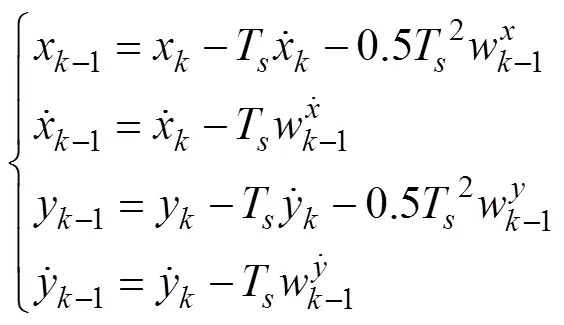
将式(12)改为矩阵形式, 即

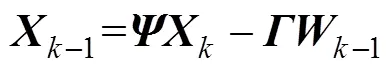
式中

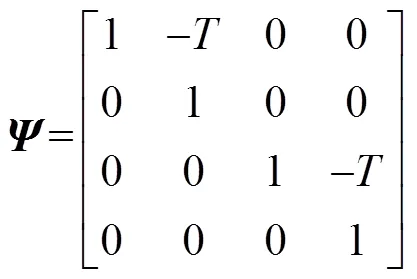
将式(13)与式(4)组成新的状态空间模型, 从而实现EKF的后向迭代, 其过程为

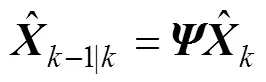
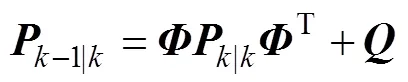
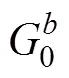
为验证所提方法的有效性, 在1.2节的条件下, 对图4中2种情况进行仿真, 并通过后向递推方法得到新的初值估计, 2种情况的初值0坐标分别为(–2, –10)和(–10, 10)。仿真结果如图5所示, 图中圆圈标记的是初值位置和后向递推更新后的初值位置。2种情况下状态估计变化情况与图4所示情况相似, 且后向递推得到的初值估计均比原始初值更接近真实值。

图4 后向迭代初值估计

基于初值更新的EKF改进方法的核心是: 通过后向迭代对目标状态初值进行重新估计, 并不断对状态初值进行更新, 使用最新更新的初值进行EKF滤波。具体步骤如下:

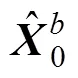
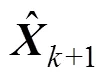
该方法在不增加新量测的情况下, 通过加强对观测数据的反复运用对初值进行更新, 从而使状态估计更容易向真实值收敛。

3 仿真试验与分析

为验证文中方法的性能, 通过仿真试验对比了该方法与常规EKF方法的跟踪效果。试验以短时观测、高速运动目标为背景, 目标起始位置为原点, 以50 kn速度向正东方向匀速运动, 观测站起始位置在目标东偏北30°方向, 距离目标250 m, 以7°提前角跟踪目标, 采样间隔0.1 s, 观测时间6 s。设过程噪声协方差强度为0.1, 观测噪声协方差为3(°)2。分别设置如下3种不同初值误差的仿真条件: 1) 初值距离误差5%, 初值速度误差2%; 2) 初值距离误差10%, 初值速度误差5%; 3) 初值距离误差20%, 初值速度误差10%。

在每种条件下进行200次蒙特卡洛试验, 利用均方根误差(root mean squared error, RMSE)来衡量2种方法的估计偏差, 其定义为

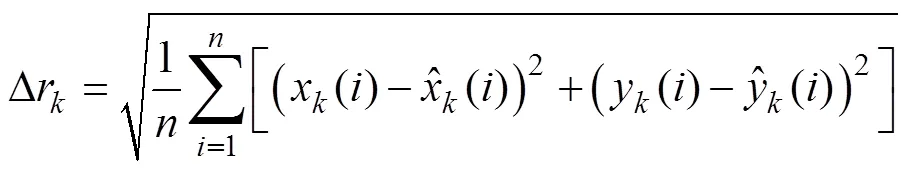
不同初值误差的条件下, 2种方法的RMSE对比分别如图6~图8所示。

根据仿真结果可以看出, 文中方法相比常规EKF方法具有更小的估计误差。随着观测时间增长, 文中方法的优势更加明显。将3种仿真条件下2种方法的RMSE进行比较, 如表1所示。对比可知, 不论是全程平均RMSE还是观测结束时的最终RMSE, 文中方法都比常规EKF方法具有更低的误差, 尤其是对观测结束时的最终误差降低效果更明显。

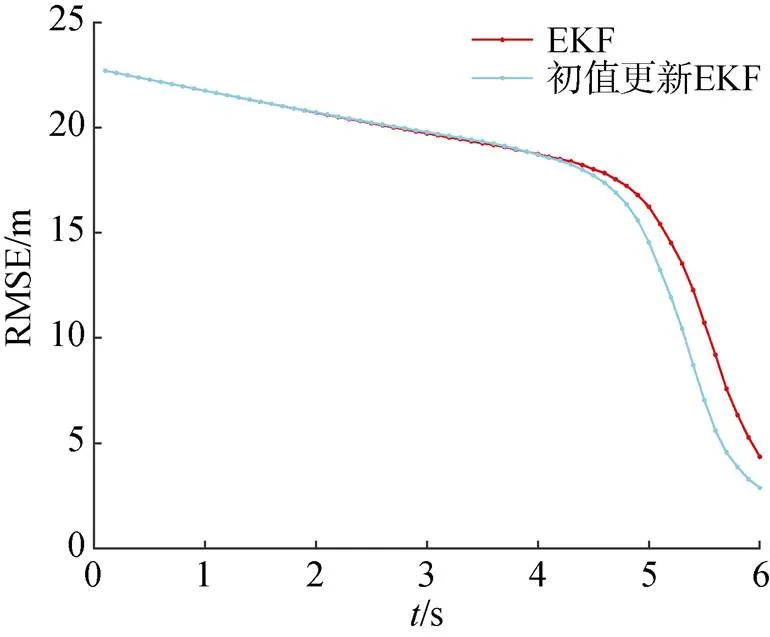
图7 试验2误差比较

图8 试验3误差比较

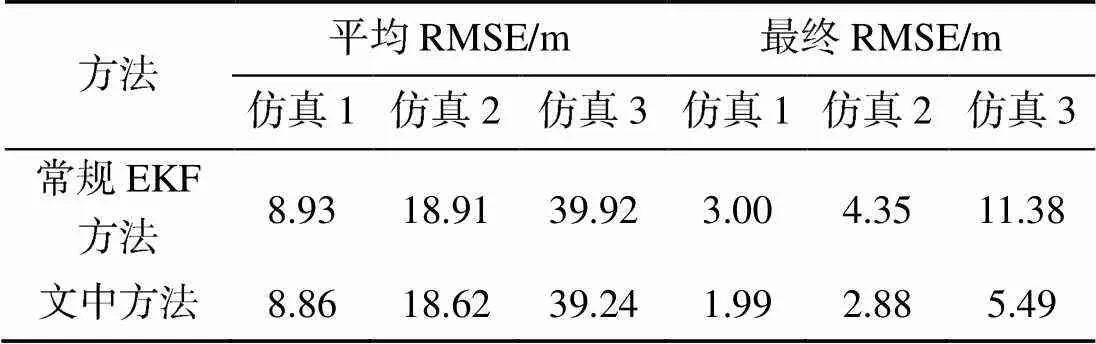
表1 2种方法RMSE比较

对比3种不同的仿真条件, 在相同的量测精度下, 最终的RMSE有着较大差异, 这是对初值依赖的表现。试验3中EKF的最终RMSE相差11.38 m, 而采用文中方法后最终RMSE仅相差5.49 m。可见文中方法通过对初值进行不断优化和更新, 减小了最终的滤波误差, 降低了对初值的依赖性。

为了验证文中方法的实时性, 采用酷睿i5 8250CPU, 在试验2条件下统计了100次试验的平均计算时间, 结果如图9所示。正如文中分析, 文中所提初值更新EKF方法与常规EKF方法相比, 计算量更大。但是计算量与EKF呈倍数关系, 而并非指数性增长。文中方法的单步计算时间在10 μs量级, 对于100 ms的采样间隔, 该方法满足工程应用的实时性要求。

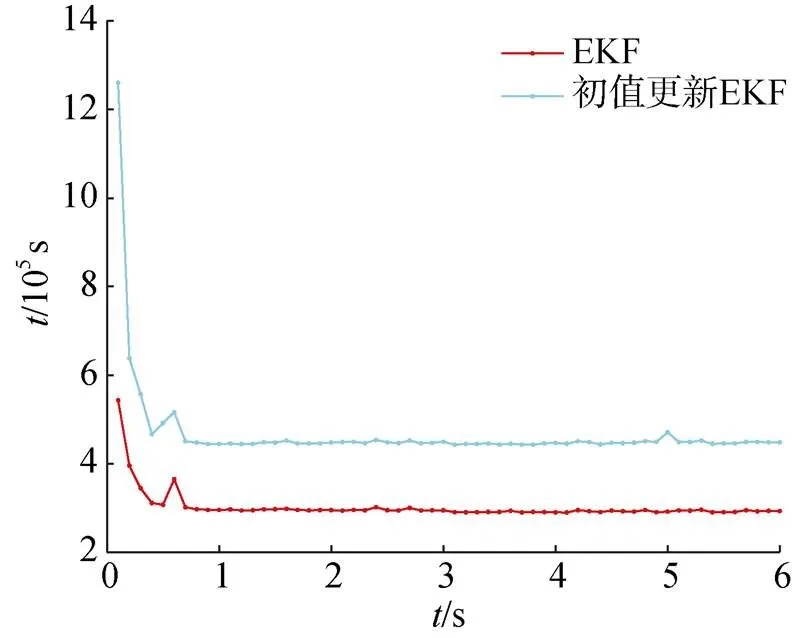
图9 计算时间比较

4 结束语

文中针对纯方位目标跟踪中滤波器对初值依赖较大的问题, 研究了纯方位目标跟踪中EKF初值选取对滤波的影响, 提出了一种基于初值更新的EKF改进方法。通过对2组不同情况下的后向递推初值估计, 证明了所提方法可使初值更接近真实值。最后通过3组初值误差不同的仿真试验进行验证, 结果表明所提方法可降低最终跟踪误差, 以减少滤波对状态初值选取的依赖。对比常规EKF, 该算法计算量更大, 更加适用于数据量较少的情形。但通过计算量的比较表明, 该方法满足工程应用的实时性要求。

下一步工作重点: 一是考虑如何有效降低算法计算量; 二是尝试该算法在更多非线性滤波场景和领域中的应用。

[1] 刘忠, 周丰, 石章松, 等. 纯方位目标运动分析[M]. 北京: 国防工业出版社, 2009.

[2] Shalom Y, Li X R, Thiagalingam K. Estimation with Applica-tions to Tracking and Navigation[M]. New York: Wiley, 2001: 381-394.

[3] Julier S J, Uhlmann J K. Unscented Filtering and Nonlinear Estimation[J]. Proc. of the IEEE, 2004, 92(3): 401-422.

[4] Carpenter J, Clifford P, Fearnhead P. An Improved Particle Filter for Non-linear Problems[J]. IEEE Proceedings-Ra- dar, Sonar and Navigation, 1999,146(1): 2-7.

[5] Li X H, Zhao C X, Yu J, et al. Underwater Bearing-only and Bearing-Doppler Target Tracking Based on Square Root Unscented Kalman Filter[J]. Entropy, 2019, 21(8): 740-756.

[6] He R, Chen S, Wu H, et al. Adaptive Covariance Feedback Cubature Kalman Filtering for Continuous-Discrete Bearings-Only Tracking System[J]. IEEE Access, 2019, 7: 2686-2694.

[7] Liu M Q, Zhang D, Zhang S L. Bearing-only Target Tracking Using Cubature Rauch-Tung-Striebel Smoother[C]//第三十四届中国控制会议论文集. 杭州: 中国自动化学会控制理论专业委员会, 2015.

[8] Razali S, Watanabe K, Maeyama S, et al. An Unscented Rauch-Tung-Striebel Smoother for a Bearing Only Tra- cking Problem[C]//ICCAS 2010. Gyeonggi-do, Korea: IEEE, 2010.

[9] Lai H C, Yang R, Ng G W, et al. Bearings-only Tracking and Doppler-Bearing Tracking with Inequality Constraint[C]//2017 Sensor Data Fusion: Trends, Solutions, Applications(SDF), Bonn, Germany: IEEE, 2017.

[10] Lin X D, Kirubarajan T, Shalom Y B, et al. Comparison of EKF, Pseudomeasurement, and Particle Filters for a Bearing-Only Target Tracking Problem[C]//SPIE, Signal and Data Processing of Small Targets. Orlando, FL, United States: SPIE, 2002: 240-250.

[11] 李绍荣, 付中, 廖平. 滤波初值对测向定位的影响及其消除方法[J]. 电子科技大学学报, 2008, 37(3): 331-334.Li Shao-rong, Fu Zhong, Liao Ping. Influence and Elimination of Algorithm Initial Value in Bearing-Only Passive Location[J]. Journal of University of Electronic Science and Technology of China, 2008, 37(3): 331-334.

[12] 余小琴, 沈文苗. 扩展卡尔曼滤波算法初值选取方法[J]. 声学与电子工程, 2012(1): 12-13,17.Yu Xiao-qin, Shen Wen-miao. Initial Value Selection Method of Extended Kalman Filter Algorithm[J]. Acoustics and Electronic Engineering, 2012(1): 12-13,17.

[13] Rong Li X, Jilkov V P. Survey of Maneuvering Target Tracking. Part I. Dynamic Models[J]. IEEE Transactions on Aerospace and Electronic Systems, 2003, 39(4): 1333- 1364.

1. 吴翔, 钟雨轩, 岳琪琪, 等. 基于深度学习的尺度自适应海面目标跟踪算法. 2020, 28(6).

2. 郑艺, 王明洲. 一种滑动后向递推的EKF纯方位目标跟踪方法. 2020, 28(6).

3. 杨向锋, 熊淑贞, 石磊. 声自导鱼雷目标跟踪误差仿真与分析. 2020, 28(5).

4. 王斌, 温泉, 范世东. 基于Huber M-CKF的UUV目标跟踪算法. 2020, 28(1).

5. 李娟, 张建新, 杨莉娟, 等. 未知环境下UUV动态目标跟踪导引方法. 2019, 27(3).

6. 张思宇, 何心怡, 张驰, 等. 水下多目标跟踪技术现状与展望. 2018, 26(6).

7. 郭龙祥, 虞涵钧, 生雪莉, 等. 基于协同探测数据融合的水下多目标跟踪. 2018, 26(5).

8. 苏骏, 李亚安, 陈晓, 等. 双观测站水下纯方位多目标跟踪的数据关联算法. 2018, 26(2).

9. 赵振轶, 李亚安, 陈晓, 等. 基于双观测站的水下机动目标被动跟踪. 2018, 26(1).

Underwater Bearings-Only Short Time Target Tracking Based on Initial Value Updating

ZHENG Yi, WANG Ming-zhou

(The 705 Research Institute, China State Shipbuilding Corporation Limited, Xi’an 710077, China)

Underwater passive bearings-only target tracking by single-observer has the advantages of simple layout and strong concealment. However, the filtering methods are sensitive to the initial value, and the actual engineering will encounter the situation of fast target speed, short observation time and less measurement data, which makes this problem significantly prominent. In view of this situation, this paper studies the causes and the effect of initial values on filtering, and presents an improved method of extended Kalman filter based on initial value update. By re-estimating and updating the initial values through backward iteration, the effect of the initial error on the filtering result is gradually reduced. The simulation results show that this method can reduce the dependence of the filter on initial value selection and the final estimation error.

bearings-only; target tracking; initial state; backward iteration

TJ630.34; TB56

A

2096-3920(2021)02-0189-07

10.11993/j.issn.2096-3920.2021.02.009

郑艺, 王明洲. 基于初值更新的水下纯方位短时目标跟踪[J]. 水下无人系统学报, 2021, 29(2): 189-195.

2020-10-13;

2020-11-04.

郑 艺(1992-), 女, 博士,主要研究方向为水下目标定位跟踪.

(责任编辑: 陈 曦)