用于单矢量水听器方位估计的加权直方图法

张小勇,张国军,尚珍珍,王帅

用于单矢量水听器方位估计的加权直方图法

张小勇1, 2, 张国军1, 尚珍珍1,王 帅2

(1. 中北大学 动态测试省部共建实验室, 山西 太原, 030051; 2. 太原学院 计算机科学与工程系, 山西 太原, 030032)

在水下无人系统中使用矢量水听器进行声源方位估计具有较大的优势, 采用加权直方图法可以利用单个矢量水听器实现方位估计, 且计算量较小。文中分析了声能流检测器的原理, 由声能流可以获得平面内声能量的分布情况, 为加权直方图法提供了理论基础。通过分析发现: 在低信噪比下, 声源的能量扩展到了真实方位之外, 使得加权直方图法的统计间隔会分割声源能量, 从而出现方位估计误差。针对这一问题, 提出了改进的基于能量搜索的加权直方图法, 该算法采用滑动窗口法寻找声源所在区间, 并利用重心法获得区间内的能量中心即方位估计的结果。通过仿真证明: 改进后的算法在统计间隔为10°, 信噪比为-10~10 dB时, 均比原算法具有更好的性能, 其均方根误差平均减小43.7%, 且在多目标(干扰)环境下的方位估计结果也更准确。文中研究可为有效改进单矢量水听器方位估计算法提供参考。

水下无人系统; 矢量水听器; 方位估计; 加权直方图; 滑动窗口法; 重心法

0 引言

水听器可有效感知水声信号, 被广泛应用于水下无人系统声源方位估计中。在无人水下航行器、潜标等设备布放空间严格受限的水下无人系统中, 标量水听器阵列因为体积较大, 使用受到了极大限制[1]。矢量水听器具有共点测量声压与声矢量的特点[2], 采用加权直方图法可以利用单个矢量水听器实现声源目标方位估计[3]。近年来出现的微机电系统(micro-electro-mechanical system, MEMS)矢量水听器兼具性能好、体积小及功耗低等优点[4]。因此, 在水下无人系统中使用矢量水听器进行方位估计具有较大的优势, 对单矢量水听器方位估计算法的研究具有重要意义。

近年来, 国内外学者对单矢量水听器方位估计领域展开了诸多研究。Nehorai[5]提出用于单矢量水听器方位估计的复声强法, 对算法的性能进行了分析, 给出了理论误差的计算方法; 孙贵青等[6]证明了在各向同性噪声场中声能流是极大似然检测, 声能流方向是声源方位的极大似然估计, 并给出了这种估计方法的克拉美罗界; 姚直象等[7]在复声强法的基础上, 提出直方图与加权直方图方位估计算法, 给出了信号处理流程, 并指出加权直方图法适用于声源包含线谱与宽带信号的情况, 而这种信号更接近现实中舰艇产生的信号。除此以外还有大量波束形成、子空间类算法研究, 这些算法的理论精度较好, 但计算复杂度较高[8], 不利于在水下无人系统中的使用。

矢量水听器在水下无人系统中使用时, 要考虑其所搭载系统的姿态变化与自身运动对测量结果的影响, 使用姿态传感器、加速度传感器等配合三维矢量水听器及相关算法, 可以对上述因素所造成的误差进行修正[9]。文中讨论了在远场平面波场中使用二维矢量水听器(矢量输出为振速)且其姿态水平的情形, 对用于单矢量水听器方位估计的加权直方图法的原理做了进一步研究, 分析了该算法存在的问题, 在此基础上提出了改进的基于能量搜索的加权直方图法, 并与原算法进行了仿真对比, 对理论进行了验证。

1 声能流检测器原理

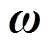
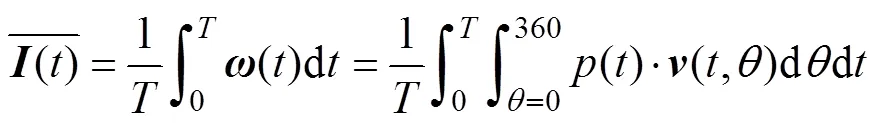
将式(1)更换积分顺序可得

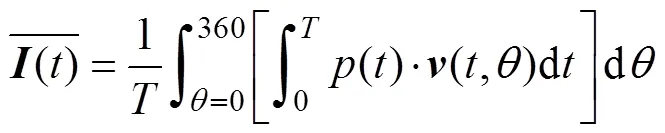
式中, 声能流检测器输出可视为对各个向上的声能流密度进行时域积分后得到每个角度对应的声能量, 再对所有角度上的能量积分。即: 声能流检测器的输出是与各角度的声能量之和正相关的量。

将式(2)变换到频域, 得

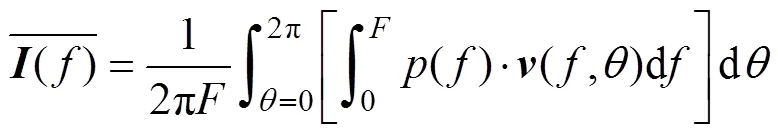
二维矢量水听器并不能直接输出声能流矢量, 它的3个输出量()、v()和v()分别为声压及振速的2个相互垂直分量的模, 声能流的模为[10]

声能流的方向可由下式获得, 该结果是对声源方位角的极大似然估计

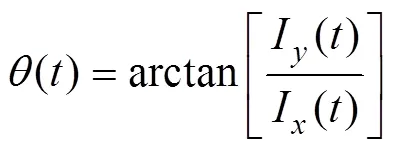
将式(4)和式(5)变换到频域时, 便可得式(3)所需各频率的声能量与方位。在各向同性高斯噪声场中, 声能流检测器的输出也可写为

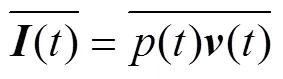
其中

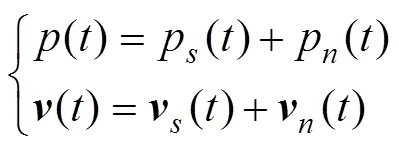
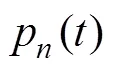
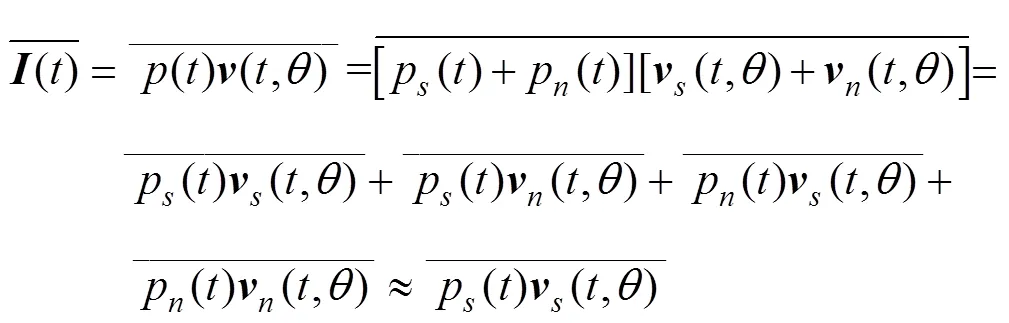
由式(8)可知, 声源与噪声不相关时, 矢量声能流检测器能够抵消各向同性噪声的干扰, 使得检测器在噪声干扰下依然能够分辨声源的声能流信号。

2 加权直方图方位估计算法

应用于单矢量水听器的加权直方图法的信号处理流程框图如图1所示。

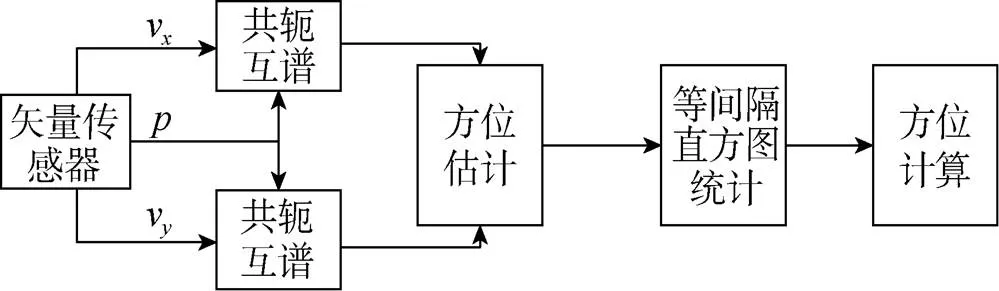
图1 加权直方图法信号处理流程框图

在海洋信道中, 近似满足声学欧姆定律, 声压与振速同相位, 根据傅里叶变换的基本特性, 2个同相位输入的能量集中在互谱的实部[12]。因此, 对式(9)的运算结果取实部便得到各频率的声能流分量()和I(), 将式(4)和式(5)变换到频域, 得到各频率的声能流模为

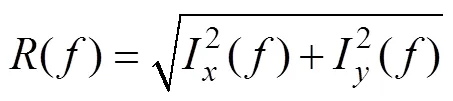
各频率声源的方位估计值为

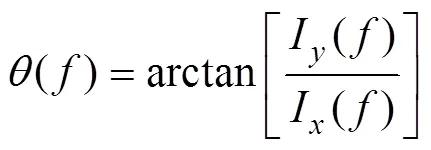
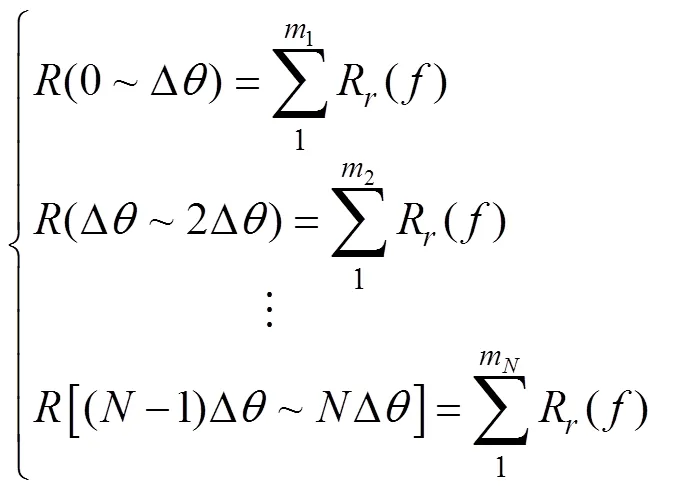
由式(8)可知, 在存在各向同性噪声时, 依然可在声源方位上获得较大的能量值, 从而在加权直方图中形成1个峰值。在加权直方图法中, 使用较小的统计间隔, 峰值所对应的角度即声源方位估计结果, 其分辨率取决于统计间隔的值, 例如: 统计间隔取1°时, 所获结果的置信区间为1°。

3 改进的加权直方图法

3.1 算法原理

由第2章可知, 使用加权直方图法对声源方位进行估计, 本质上是寻找声源能量所在方位。在低信噪比下使用加权直方图法对声能量的分布情况进行仿真, 仿真条件为: 信噪比0 dB, 噪声为与声源不相关的高斯噪声, 采样率4 kHz, 采样时间1 s, 声源为连续谱宽带信号(10~500 Hz), 方位为20°。仿真得到的声能量分布如图2所示。

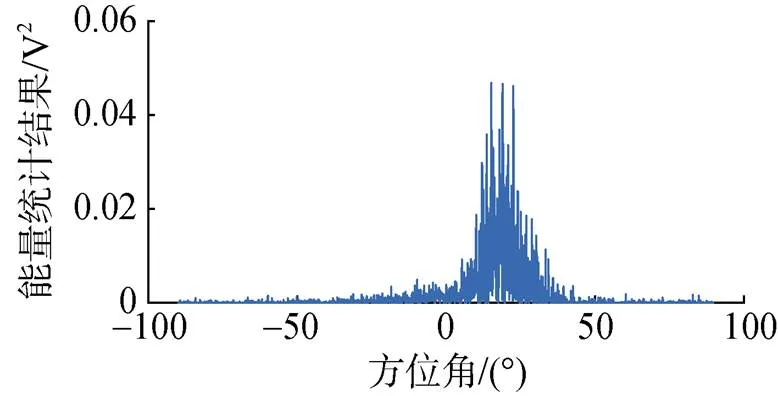
图2 信噪比为0 dB时声能量分布图

由图2可知, 信噪比较低时, 在声源方位附近形成了1个峰, 但声源能量在真实方位之外较大的范围内均存在, 且分布图上的峰值不一定是真实方位。这种情况下使用加权直方图法, 在较小的统计间隔下, 必然造成声源能量被分割在不同的统计间隔中, 真实方位所在统计间隔的能量不一定是最大的, 从而引起方位估计误差。为避免这种情况, 文中提出一种改进的基于能量搜索的加权直方图法, 其信号处理流程如图3所示。

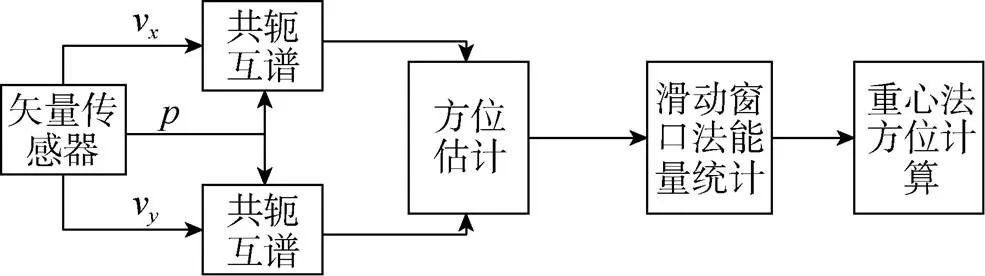
图3 改进算法信号处理流程框图

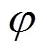
然后, 进一步在这一区间中确定声源的方位。由于已经获得了能量的分布情况, 这里使用能量重心法计算能量中心所在位置, 并以此位置作为方位估计结果。能量重心法基于对称窗函数功率谱的能量重心特性, 在得到声源所在的统计间隔后, 将该区间的各个角度及其对应的声能流值代入下式即得到目标方位角[15]

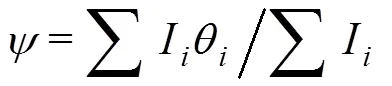
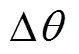
3.2 实验与结果分析

均方根误差用来衡量观测值与真实值之间的偏差, 能够很好地反映出测量的准确度, 其值是测量值与真实值偏差的平方和与观测次数比值的平方根。文中采用均方根误差这一指标对算法的性能进行验证与分析。

为了验证统计间隔对改进算法的影响, 进行如下仿真。仿真条件为: 信噪比0 dB, 噪声为与声源不相关的高斯噪声, 采样率4 kHz, 采样时间1 s, 声源为连续谱宽带信号(10~500 Hz), 方位20°, 统计间隔由1°~10°, 滑动步距0.1°。仿真次数1 000次, 仿真结果如图4所示。

由仿真结果可知, 方位估计结果的均方根误差随着统计间隔的增加而减小, 在10°附近均得到较小的值, 且基本达到稳定。这表明: 随着统计间隔的增加, 被测声源能量更多的被纳入统计间隔之中时, 增大了方位估计的准确性, 从而有效判断区间内能量中心的所在位置。

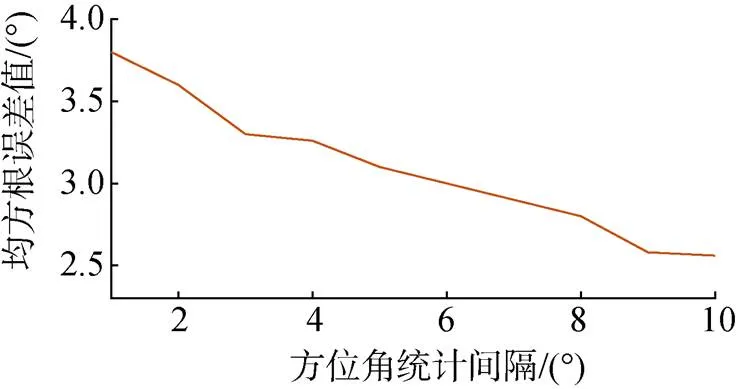
图4 不同统计间隔下的仿真结果

图5 不同信噪比下的仿真结果Fig. 5 Simulation results under different SNRs

由仿真结果可知: 当信噪比为–10~10 dB时, 2种算法的方位估计结果均随着信噪比的增加而改善, 改进算法的估计结果在各个信噪比均优于原算法; 均方根误差平均减小了43.7%, 这表明所获数据的准确性有所提高。

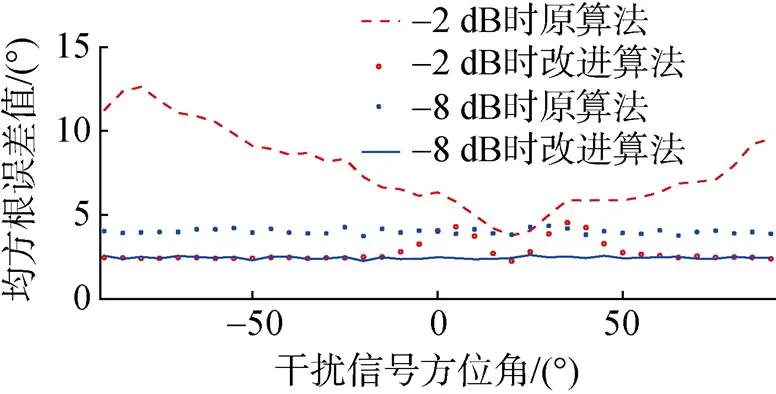
图6 干扰信号与目标频带不同时的仿真结果

其他条件不变的情况下, 在干扰信号为连续谱宽带信号(10~500 Hz), 即与目标声源频带相同时进行仿真, 各条件下的仿真次数均为1 000次。仿真结果如图7所示。

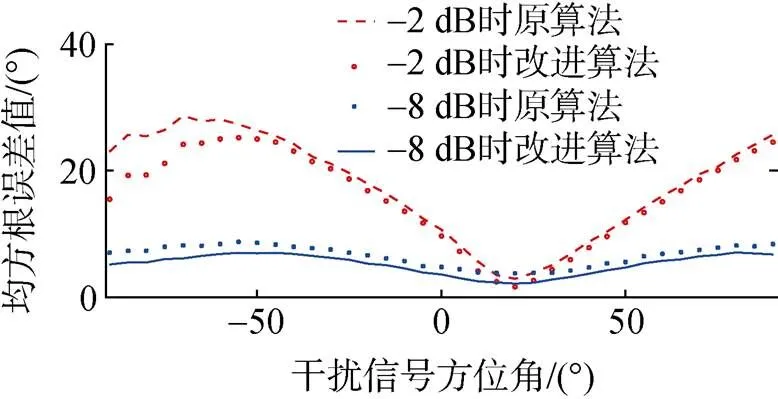
图7 干扰信号与目标频带相同时的仿真结果

4 结束语

[1] 申辉. 基于纤毛式纳机电矢量水听器的潜标系统设计与实现[D]. 太原: 中北大学, 2015.

[2] Zhang G P, Zheng C, Lin W S, et al. Steering Acoustic Intensity Estimator Using a Single Acoustic Vector Hydrophone[J]. Journal of sensors, 2018(3): 1-10.

[3] Anbang Z, Lin M, Juan H, et al. Open-Lake Experimental Investigation of Azimuth Angle Estimation Using a Single Acoustic Vector Sensor[J]. Journal of Sensors, 2018(3): 1-11.

[4] Zhang X Y, Xu Q D, Zhang G J, et al. Design and Analysis of a Multiple Sensor Units Vector Hydrophone[J]. Aip Advances, 2018(8): 085124.

[5] Nehoral A. Acoustic Vector Sensor Array Processing[J]. IEEE Trans．Signal Processing, 1994(9): 2481-2491.

[6] 孙贵青, 杨德森, 张揽月, 等. 基于矢量水听器的最大似然比检测和最大似然方位估计[J]. 声学学报, 2003, 28(1): 66-72.Sun Gui-qin, Yang De-sen, Zhang Lan-yue, et al. Maximum Likelihood Ratio Detection and Maximum Likelihood DOA Estimation Based on the Vector Hydrophone[J]. Acta Acustica, 2013, 28(1): 66-72.

[7] 姚直象, 惠俊英, 殷敬伟, 等. 基于单矢量水听器四种方位估计方法[J]. 海洋工程, 2006, 24(1): 122-127.Yao Zhi-xiang, Hui Jun-yin, Yin Jin-wei, et al. Four Approaches to DOA Estimation Based on a Single Vector Hy- drophone[J]. The Ocean Engineering, 2006, 24(1): 122-127.

[8] 曾雄飞, 孙贵青, 李宇, 等. 单矢量水听器的几种DOA估计方法[J]. 仪器仪表学报, 2012, 33(3): 499-507.Zeng Xiong-fei, Sun Gui-qin, Li Yu, et al. Several Approaches of DOA Estimation for Single Vector Hydrophone[J]. Chinese Journal of Scientific Instrument, 2012, 33(3): 499-507.

[9] 孙芹东. 一种新型姿态实时修正矢量水听器的设计[C]// 中国声学学会水声学分会2015年学术会议论文集. 武汉: 中国声学学会水声学分会, 2015.

[10] 杨德森, 洪连进. 矢量水听器原理及应用引论[M]. 北京: 科学出版社, 2009.

[11] 李春旭, 王逸林, 梁国龙. 平均声强器性能分析[C]//中国声学学会1999年青年学术会议论文集. 武汉: 中国声学学会, 1999.

[12] 姚直象, 惠俊英, 蔡平, 等. 单矢量水听器方位估计的柱状图方法[J]. 应用声学, 2006, 25(3): 161-167.Yao Zhi-xiang, Hui Jun-yin, Cai Pin, et al. A Histogram Approach of the Azimuth Angle Estimation Using a Single Vector Hydrophone[J]. Applied Acoustics, 2006, 25(3): 161-167.

[13] 彭策. 单矢量水听器被动定位方法研究[D]. 哈尔滨: 哈尔滨工程大学, 2014.

[14] 吴鹏, 赵风海, 黄洋. 一种结合线性预测倒谱法和组合滑动窗口平滑法的基音周期估计改进算法[J]. 南开大学学报(自然科学版), 2019, 52(2): 29-33.Wu Peng, Zhao Feng-hai, Huang Yang. An Improved Pitch Period Estimation Cepstrum Algorithm Combined Linear Prediction and Sliding Window Smoothing[J]. Acta Sci- entiarum Naturalium Universitatis Nankaiensis(Natural Science Edition), 2019, 52(2): 29-33.

[15] 陈平, 王佳昌, 吴兴研. 能量重心法的改进FFT算法分析及应用研究[J]. 机械科学与技术, 2018, 37(12): 1883-1889.Chen Ping, Wang Jia-chang, Wu Xing-yan. Analysis and Application of an Improved FFT Algorithm for Energy Centrobaric Correction Method[J]. Mechanical Science and Technology for Aerospace Engineering, 2018, 37(12): 1883-1889.

[16] 惠俊英, 惠娟. 矢量声信号处理技术[M]. 北京: 北京国防工业出版社, 2004.

Weighted Histogram Method for DOA Estimation Using Single Vector Hydrophone

ZHANG Xiao-yong1, 2, ZHAGN Guo-jun1, SHANG Zhen-zhen1, WANG Shuai2

(1. State Key Laboratory of Dynamic Testing Technology, North University of China, Taiyuan 030051, China; 2. Department of Computer Science and Engineering, Taiyuan University, Taiyuan 030032, China)

unmanned undersea system; vector hydrophone; direction of arrival(DOA) estimation; weighted histogram; slide window method; gravity center method

TJ630.34; TB566

A

2096-3920(2021)02-0164-06

10.11993/j.issn.2096-3920.2021.02.005

张小勇, 张国军, 尚珍珍, 等. 用于单矢量水听器方位估计的加权直方图法[J]. 水下无人系统学报, 2021, 29 (2): 164-169.

2020-04-27;

2020-07-30.

国家自然科学基金项目资助(61525107, 61727806).

张小勇(1982-), 男, 在读博士, 副教授, 主要研究方向为矢量水听器及其信号处理.

(责任编辑: 杨力军)