随机错位组合阵列分级波束旁瓣控制方法
2021-05-15杜金香
祝 鹏, 杜金香
随机错位组合阵列分级波束旁瓣控制方法
祝 鹏, 杜金香
(西北工业大学 航海学院, 陕西 西安, 710072)
为了降低水下大型声呐阵列波束形成算法的工程实现难度, 可采用阵元级分区波束扫描模式的大型平面阵列, 无需改变每个扫描分区内的阵元幅相权, 仅通过子阵级数字波束形成即可完成阵列的波束扫描。但该模式会带来高旁瓣问题。针对此, 文中提出一种基于规则子阵的随机错位组合阵列设计方法, 打破现有研究方法中错位量为整数倍阵元间距的限制, 利用遗传算法同时对子阵相邻列错位量与子阵级权系数进行联合优化, 以主旁瓣比作为适应度函数, 使得综合方向图最高旁瓣最低, 从而降低了由于子阵级大阵元间距带来的栅瓣效应。仿真结果表明, 采用随机错位的子阵结构, 优化后的阵型和权系数能够有效避免大分区下带来的高旁瓣, 在不同分区内都能获得较高的主旁瓣比, 对于旁瓣的控制效果优于现有错位组合阵列方法, 验证了随机错位组合阵列设计优化方法的有效性。
声呐阵列; 随机错位; 旁瓣控制; 分区扫描; 组合阵列; 遗传算法
0 引言
随着海洋开发、海洋勘探及水下作战等领域的不断深入发展, 大型声呐阵以及数字波束形成技术得到越来越广泛的应用[1]。大型阵列进行阵元级集中波束形成在工程实现上由于数字接收通道多, 对于数据存储和处理的实时性提出了更高的要求, 这就导致了硬件复杂度增加, 成本高昂。分级波束形成是解决这一问题的重要途径之一。
分级波束形成将阵列按照一定的规则划分为多个子阵, 每个子阵形成1个通道, 通过对子阵进行数字加权形成期望波束。子阵划分方式主要有规则不重叠子阵、规则重叠子阵和不规则不重叠子阵。不规则不重叠子阵能够很好地降低子阵级带来的栅瓣影响[2], 但是结构复杂。而规则子阵由于结构简单、算法较易实现, 仍然是分级波束形成的重要研究对象[3-4]。
规则子阵划分方法按照排布方式可分为邻接子阵、重叠子阵与错位子阵等[5]。邻接子阵在扫描过程中周期出现的栅瓣会导致方向图形成高旁瓣, Mailloux[6]基于规则子阵给出了简单的近似公式和拟合曲线来评估栅瓣水平。重叠子阵通过子阵复用阵元减小子阵中心间距, 有利于栅瓣抑制[7-9], 但是阵元的复用导致拓扑结构复杂, 不易于工程实现。Wang等[10]结合重叠子阵技术提出子阵周期错位排列的等效重叠阵列思想, 在均匀平面阵的基础上调整位置关系, 使相邻列沿列方向错位1个阵元间距, 降低了俯仰方向的栅瓣效应, 不足之处在于阵列三维方向图其他角度上的栅瓣无法避免。黄飞等[11]在等效重叠阵列的基础上提出相邻列错位整数倍阵元间距的随机错位布阵方式, 对于子阵规模为4个子阵的仿真实例, 错位量在0~3中随机选择(为阵元间距), 采用粒子群算法取波束指向的俯仰角绝对值最大的4个波束指向作为代表进行优化, 在扫描范围内取得了较低的旁瓣, 但有限的错位组合和扫描范围限制了性能的进一步提升。除此之外, 其他的错位方法也有相应研究, 比如杨功清等[12]以规则矩形子阵几何中心为优化变量, 每个子阵在八边形阵面不重叠地随机分布, 通过在子阵间增加平移错位量, 使得方向图的高旁瓣得到有效降低。
文中首先介绍了阵元级分区波束扫描技术及其高旁瓣形成原理, 提出一种平面阵列的错位组合阵列优化设计方法, 突破现有研究方法中错位量为整数倍阵元间距的限制, 最后利用遗传算法对错位量及子阵级权系数进行联合优化, 优化后的错位组合阵型和权系数在一定范围的扫描分区内都能获得较低的旁瓣级。
1 阵元级分区波束扫描高旁瓣形成原理
为了降低大型阵列波束形成算法工程实现难度, 阵元级采用大间距扫描, 即分区扫描, 子阵级使用高精度扫描。将阵元级的扫描区间划分为若干分区, 阵元级移相器在同一分区内保持不变, 由子阵级移相器的不断变化来完成扫描工作。基于阵元级分区波束扫描模式的子阵划分结构图如图1所示。

图1 子阵划分结构图
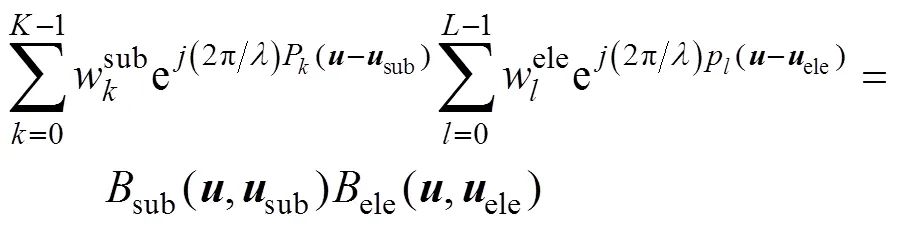

由上式可知, 规则子阵划分的综合波束方向图为阵元级、子阵级方向图的乘积, 当两级阵因分区波束扫描导致预形成波束指向角度不同时, 若子阵级的栅瓣位置处所对应的阵元级输出增益过高, 将会导致综合波束方向图出现高旁瓣。例如, 采用规则划分为5子阵的25阵元均匀线列阵, 阵元间距半波长, 两级均采用等加权, 阵元级指向40°, 子阵级分别指向40°和30°, 仿真结果如图2~3所示。可以发现, 如果两级波束指向相同时, 子阵级栅瓣出现的位置与阵元级的零点位置相同, 栅瓣将被抑制; 采用阵元级分区波束扫描模式导致两级波束指向不同时, 栅瓣出现的位置对应的阵元级方向图输出增益过高, 栅瓣未被抑制并产生高旁瓣。因此, 需要进行合理的优化设计以实现旁瓣控制, 从而获得较低的旁瓣级。
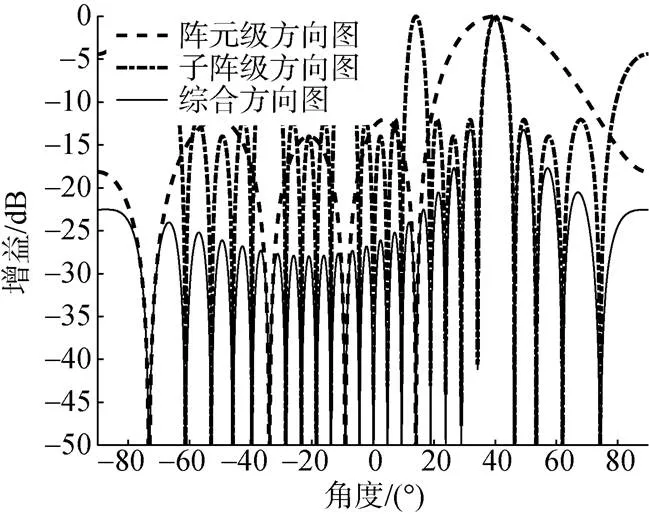
图2 两级指向角度相同时综合方向图
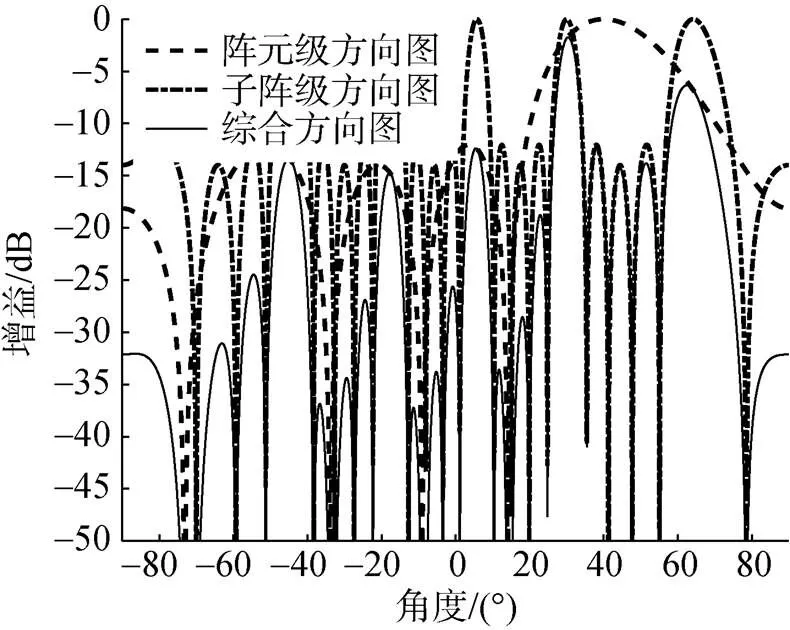
图3 两级指向角度不同时综合方向图
2 错位组合阵列优化设计
对于大型子阵阵列结构, 影响综合波束方向图性能的主要因素包括子阵阵因子(阵元级方向图)和子阵方向图(子阵级方向图)。常见的非规则子阵划分通过影响子阵阵因子获得低旁瓣的综合方向图。错位组合子阵结构则主要从控制子阵方向图的角度来影响综合方向图性能, 一般采用规则的子阵结构铺满整个阵面, 通过子阵间的几何错位来抑制大间距引起的栅瓣效应, 从而实现旁瓣控制。
2.1 随机错位组合结构
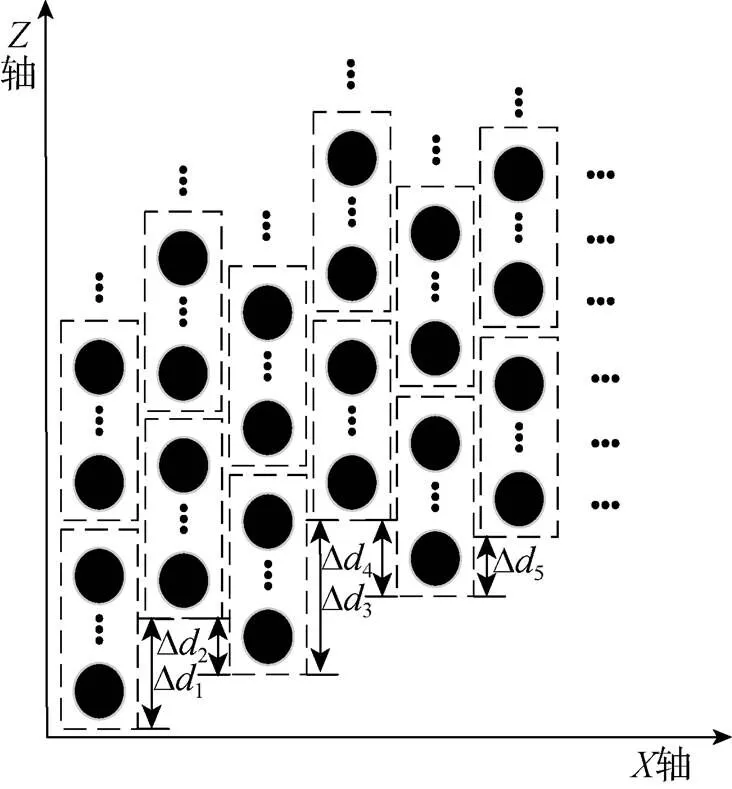
图4 随机错位组合子阵结构


可以发现, 随机的子阵排布方式打乱了子阵方向图规则的大子阵间距, 当子阵方向图的高副瓣与子阵阵因子的低增益点对齐时就可以获得较好的旁瓣控制效果; 同时, 非整数倍阵元间距的错位量减少了错位组合的组合限制, 增加了子阵排布的自由性, 可以获得更高的主旁瓣比。
2.2 优化问题求解
遗传算法(genetic algorithm, GA)模拟自然界的淘汰和遗传法则, 通过群组对比搜索, 达到对参数空间的快速有效搜索, 非常适用于处理传统搜索算法难以解决的复杂和非线性优化问题。基于此, 将上文中的阵元级分区波束扫描模式应用于平面阵优化, 并使用GA来解决上述的联合优化问题。


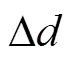

式中:为阵列列数;为每一列线型子阵个数。变量的保留位数由随机量精度确定。
3 仿真结果与分析

图5 整数倍阵元间距子阵结构综合方向图
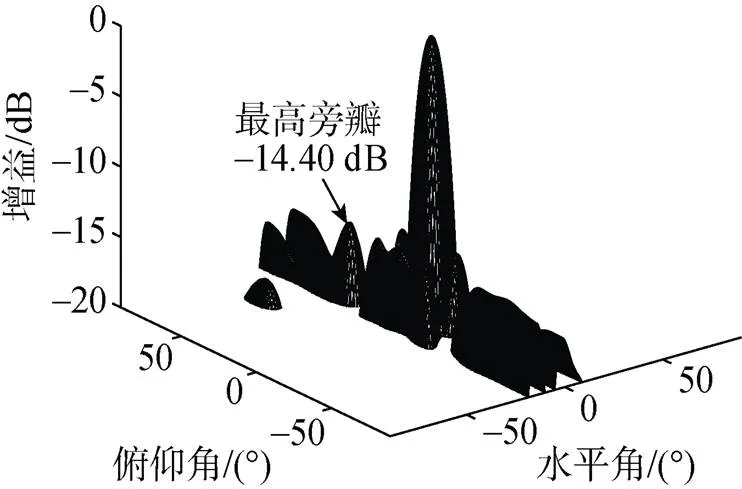
图6 随机错位子阵结构综合方向图

表1 子阵级主轴指向不同角度下最高旁瓣
将该优化结果应用于其他分区, 表2列出了不同分区极限扫描角度下的最高旁瓣。

表2 不同分区极限扫描角度下最高旁瓣
由表1可以看出, 在子阵级指向分区极限角度下优化的子阵错位结构和子阵级权系数对于当前分区内其他指向角度仍然具有较低的旁瓣级。
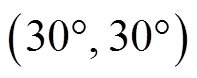
4 结束语
规则子阵划分方法虽然容易引起高旁瓣问题, 但其构造方法简单, 在工程实现上仍具有较多优势。文中以平面阵为例, 阵列工作采用阵元级分区波束扫描模式, 对相邻列子阵随机错位量及子阵级权系数联合优化, 突破了现有文献中错位量为阵元间距整数倍的限制, 得到了更低的最高旁瓣; 以扫描分区内某一极限角度计算获得的优化结果适用于当前分区以及一定范围的其他分区内的所有扫描角度, 降低了大型阵列算法实现的复杂度。
由于水下应用环境存在一定程度的误差, 同时文中使用的联合优化遗传算法收敛速度较慢, 后续将对优化结果的阵元位置误差稳健性进行进一步的研究, 并力求降低算法的时间复杂度。
[1] 熊子源. 阵列雷达最优子阵划分与处理研究[D]. 长沙: 国防科学技术大学, 2015.
[2] 程乃平, 潘点飞. 大型阵列天线子阵划分及栅瓣抑制方法[J]. 信号处理, 2014, 30(5): 535-543.Cheng Nai-ping, Pan Dian-fei. Subarray Partition Method and Grating Lobe Suppression for Large Array Antenna[J]. Journal of Signal Processing, 2014, 30(5): 535-543.
[3] 王景梅. 基于规则子阵的数字波束形成及旁瓣对消[D].西安: 西安电子科技大学, 2014.
[4] 江禹生, 周勋, 刘枫. 基于遗传算法的均匀子阵数字多波束形成研究[J]. 系统仿真技术, 2008, 4(2): 102-106 .Jiang Yu-sheng, Zhou Xun, Liu Feng. Study on DBF for Multi-beam at Uniform Subarray Level Based on Genetic Algorithms[J] .System Simulation Technology, 2008, 4(2): 102-106.
[5] 陈碧仙, 金荣洪, 耿军平, 等.均匀邻接子阵的栅瓣抑制[J].上海交通大学学报, 2011, 45(3): 340-344.Chen Bi-xian, Jin Rong-hong, Geng Jun-ping, et al.Beam Scanning Uniform Subarray Scanning Regional Division Particle Swarm Optimization(PSO) Beamforming[J]. Jour- nal of Shanghai Jiaotong University, 2011, 45(3): 340- 344.
[6] Mailloux R. Array Grating Lobes Due to Periodic Phase, Amplitude, and Time Delay Quantization[J]. IEEE Tran- sactions on Antennas & Propagation, 1984, 32(12): 1364- 1368.
[7] 丁婷, 赵拥军. 基于重叠子阵的毫米波大规模MIMO混合预编码算法[J]. 信息工程大学学报, 2019, 20(5): 5-11, 17.Ding Ting, Zhao Yong-jun.Overlapped Subarray Based Hybrid Precoding for mm Wave Massive MIMO[J].Jo- urnal of Information Engineering University, 2019, 20(5): 5-11, 17.
[8] 娄昊, 张群, 朱丰, 等. 基于交错稀疏阵列优化的雷达-通信共享孔径方法[J].电光与控制, 2018, 25(2): 83-87.Lou Hao, Zhang Qun, Zhu Feng, et al.Radar/Commu- nication Antenna Aperture Sharing Based on Staggered Sparse Antenna Array Optimization[J].Electronics Optics & Control, 2018, 25(2): 83- 87.
[9] 陈建锋, 吴海. 基于子阵重叠结构的子阵划分技术研究[J]. 舰船电子对抗, 2016, 39(1): 95-98 .Chen Jian-feng, Wu Hai. Research into Subarray Division Technology Based on Overlapped Subarray Architectu- re[J]. Shipboard Electronic Countermeasure, 2016, 39(1): 95-98.
[10] Wang L L, Fang D G, Sheng W X. An Equivalent Overlapping Array with Optimized Sub-Array Pattern[C]// 2002 3rdInternational Conference on Microwave and Millimeter Wave Technology. Beijing: IEEE, 2002.
[11] 黄飞, 盛卫星, 马晓峰.随机错位子阵阵列天线及其优化设计[J].电波科学学报, 2008, 23(5): 917-921. Huang Fei, Sheng Wei-xing, Ma Xiao-feng.Plane Ante- nna Arrays with Randomly Staggered Subarrays and Its Optimal Design[J].Chinese Journal of Radio Science, 2008, 23(5): 917-925.
[12] 杨功清, 徐振海, 董玮.错位子阵波束形成与优化设计[J].现代雷达, 2019, 41(9): 1-3.Yang Gong-qing, Xu Zhen-hai, Dong Wei. Beamforming and Optimization Design of Displaced Subarrays[J]. Mo- dern Radar, 2019, 41(9): 1-3.
1. 王莎, 施博, 郝程鹏. 基于斜对称阵列的水下单脉冲降维空时自适应处理. 2020, 28 (2).
2. 张舒皓, 马晓川, 杨力, 等. 基于多片高性能DSP的主动声呐低速运动小目标探测系统. 2019, 27(6).
3. 朱少豪, 杨益新, 汪勇. 基于协方差矩阵特征向量的圆环阵目标方位估计方法. 2019, 27(4).
4. 苏梦娜, 梁红, 杨长生. 基于SCAT模型的水下多目标高分辨仿生成像方法. 2019, 27(2).
5. 胡桥, 刘钰, 赵振轶, 等. 水下无人集群仿生人工侧线探测技术研究进展. 2019, 27(2).
6. 朱峰, 朱元林, 刘松海. 一种基于互谱法的鱼雷末弹道定位方法. 2019, 27(1).
7. 张倩, 梁红, 杨长生. 基于四元稀疏T型阵的AUV方位估计算法. 2019, 27(1).
8. 张红梅, 陈明杰, 刘洪丹, 等. 基于CS和随机声呐阵列的水下目标方位估计. 2018, 26(6).
9. 朱少豪, 杨益新, 汪勇. 圆柱阵特征波束分解与综合超指向性波束形成方法. 2018, 26(5).
10. 戚茜, 陈航, 周标. 水下噪声源可视化识别系统设计与实现. 2018, 26(4).
11. 汪勇, 杨益新, 马远良. 圆环形声学传感器阵列超指向性理论及方法. 2017, 25(5).
Side Lobe Control Method in Subarray Beamforming Based on Randomly Staggered Combination Array
ZHU Peng, DU Jin-xiang
(School of Marine Science and Technology, Northwestern Polytechnical University, Xi’an 710072, China)
In order to reduce the difficulty of engineering implementation of the underwater large-scale sonar array beamforming algorithm, a large planar array with element-level partitioned beam scanning mode can be adopted, without changingthe weight of amplitude and phase of the array element in each scanning partition, and only the subarray-level digital beamforming is adopted, then the beam scanning of the array can be completed. However, this mode will bring high side lobe problems. To solve this problem, a new method of randomly staggered combination array based on regular subarray division is proposed, which breaks the limit of the existing research method that the offset is an integer multiple of the element spacing, and uses genetic algorithm to simultaneously optimize the offseof adjacent columns of the subarray and the subarray-level weight coefficients. The main side lobe ratio is used as the fitness function. Hence, the highest side lobe of the integrated pattern is the lowest and the grating lobe effect caused by the large element spacing at the subarray level is reduced. The simulation results show that the use of random staggered subarray structure, the optimized formation and weight coefficients can effectively avoid the high side lobe in large partitions and obtain a higher main side lobe ratio in different partitions. The control effect of the side lobes is better than that of the existing staggered combination array method, which verifies the effectiveness of the proposed method.
sonar array; randomly staggered subarray; side lobe control; regional division scanning; combination array; genetic algorithm
TJ630.34; TN820 .1
A
2096-3920(2021)02-0183-06
10.11993/j.issn.2096-3920.2021.02.008
祝鹏, 杜金香. 随机错位组合阵列分级波束旁瓣控制方法[J]. 水下无人系统学报, 2021, 29(2): 183-188.
2020-08-05;
2020-12-03.
祝 鹏(1993-), 男, 在读硕士, 主要研究方向为阵列信号处理.
(责任编辑: 杨力军)
