谈拉格朗日方程在高中物理竞赛中的应用

孙 伟

(南京市雨花台中学,江苏 南京 210012)

对高中物理力学竞赛题的处理基本上是以牛顿运动定律来求解的,而用牛顿运动定律来求解质点组的运动问题时,常常要解算大量的微分方程组.如果质点组受到约束,则因约束反力都是未知的,所以并不能因此减少而且甚至增加了问题的复杂性.为此,利用分析力学的思路解决这类问题往往相对简单.下面对拉格朗日方程的应用做简单介绍.

1 完整约束

某些约束仅对力学系统的几何形象加以限制,即仅对系统的位形加以限制,而对质点的速度没有限制,这种约束称为几何约束.对于涉及力学系统运动情况的约束,即对速度也有限制的,则称为运动约束.可积分的运动约束与几何约束在物理实质上没有区别,合称为完整约束.

2 保守力系的拉格朗日方程

3 应用步骤

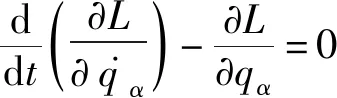
题1.(第30届决赛)质量均为m的小球1和小球2由一质量可忽略、长度为l的刚性轻杆连接,竖直地靠在墙角,如图1所示.假设墙和地面都是光滑的.初始时给2一个微小的向右的初速度.问系统在运动过程中,当杆与竖直墙面之间的夹角为何值时,球1开始离开墙面?

图1

解析: 球1开始离开墙面前两球各自沿直线运动,它们的运动受到一个刚性杆的限制,因此系统只有1个自由度.建立如图2所示的坐标系,取杆与竖直墙面的夹角θ为广义坐标,此时球1的y轴坐标为

y=lcosθ.

(1)

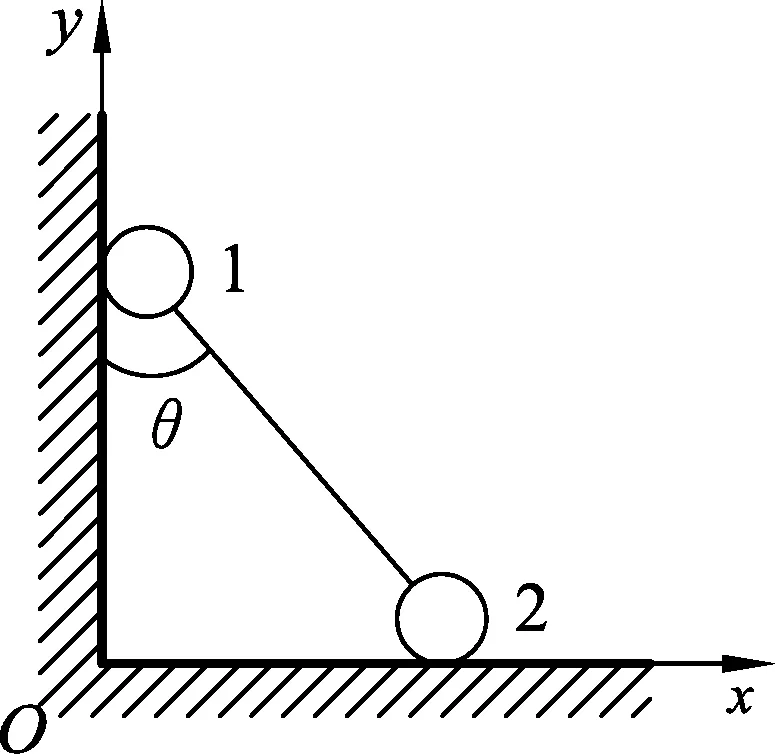
图2

球2的x轴坐标为

x=lsinθ.

(2)

(1)(2)式分别对时间求导得:球1的的速度

(3)

球2的速度

(4)

主动力为两球的重力,它们为保守力.系统的动能

(5)

系统势能

V=mglcosθ.

(6)

拉格朗日函数

L=T-V.

(7)

由(3)～(7)式得

(8)

由拉格朗日方程得

(9)

由(9)式得

(10)

对(10)式积分并代入初始条件得

(11)

球1脱离墙面时,杆对两球没有作用力,球2的加速度为零,对(4)式求导得

(12)

联立(10)～(12) 3式得

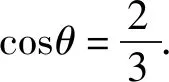
(13)

题2.(第33届决赛)如图3所示,AB为一根均质细杆,质量为m,长度为l2;杆上端B通过一不可伸长的软轻绳悬挂到固定点O,绳长为l1.开始时绳和杆均静止下垂,此后所有运动均在同一竖直面内.

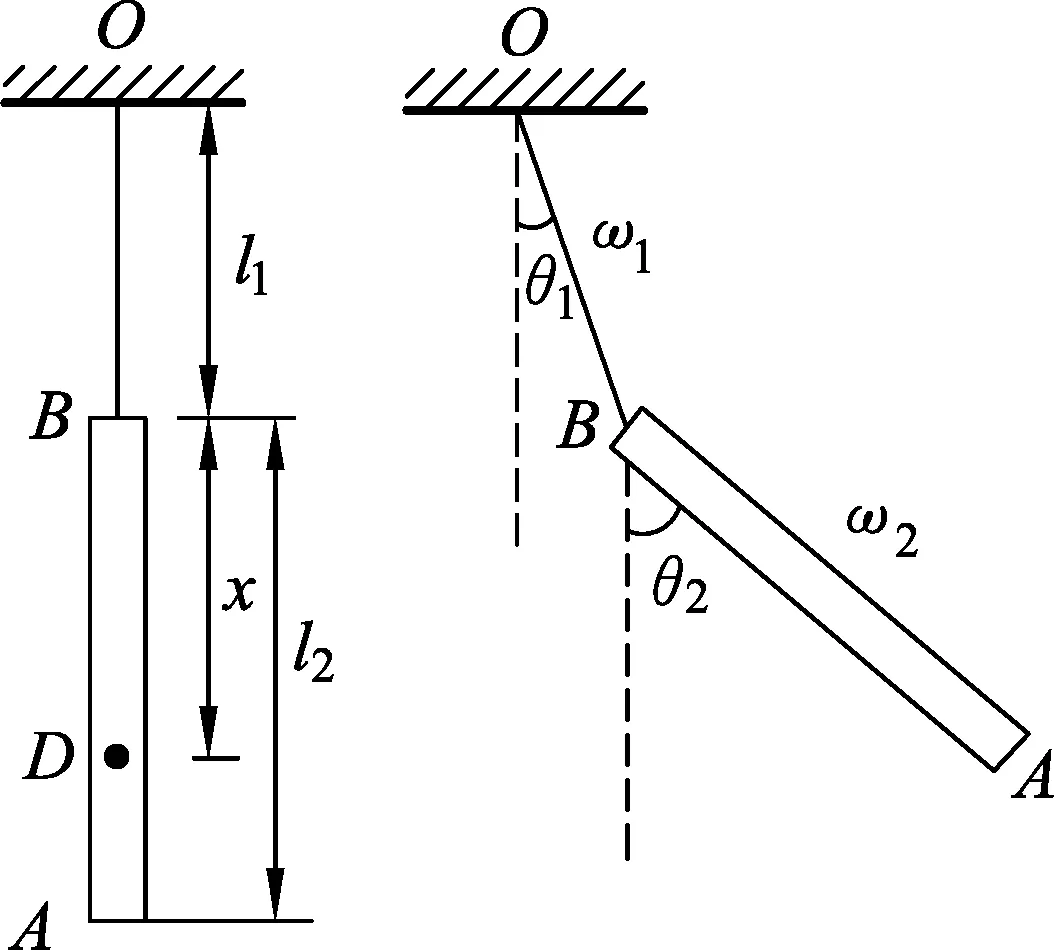
图3 图4

(1) 现对杆上的D点沿水平方向施加一瞬时冲量I,若在施加冲量后的瞬间,B点绕悬点O转动的角速度和杆绕其质心转动的角速度相同,求D点到B点的距离和B点绕悬点O转动的初始角速度ω0.

(2) 设在某时候,绳和杆与竖直方向的夹角分别为θ1和θ2(如图4所示),绳绕固定点O和杆绕其质心转动的角速度分别为ω1和ω2,求绳绕固定点O和杆绕其质心转动的角加速度α1和α2.

解析: (1) 设在施加冲量后的瞬间杆的质心C速度为vC,由冲量定理得

I=mvC.

(1)

由刚体转动定理得

(2)

B、C点以同一角速度绕O点转动,B点速度满足

(3)

由(1)(2)(3)式得

(4)

(2) 系统有2个自由度,以绳和杆与竖直方向的夹角θ1和θ2作为系统的广义坐标.建立以点O为原点,水平向右为x轴,竖直向下为y轴的坐标系,则杆的质心坐标为

(5)

(5)式对时间求导得质心速度

(6)

主动力为杆的重力,是保守力.系统的动能为

(7)

系统的势能

(8)

拉格朗日函数

L=T-V.

(9)

由拉格朗日方程得

(10)

(11)

由(10)、(11)式得

(12)

(13)

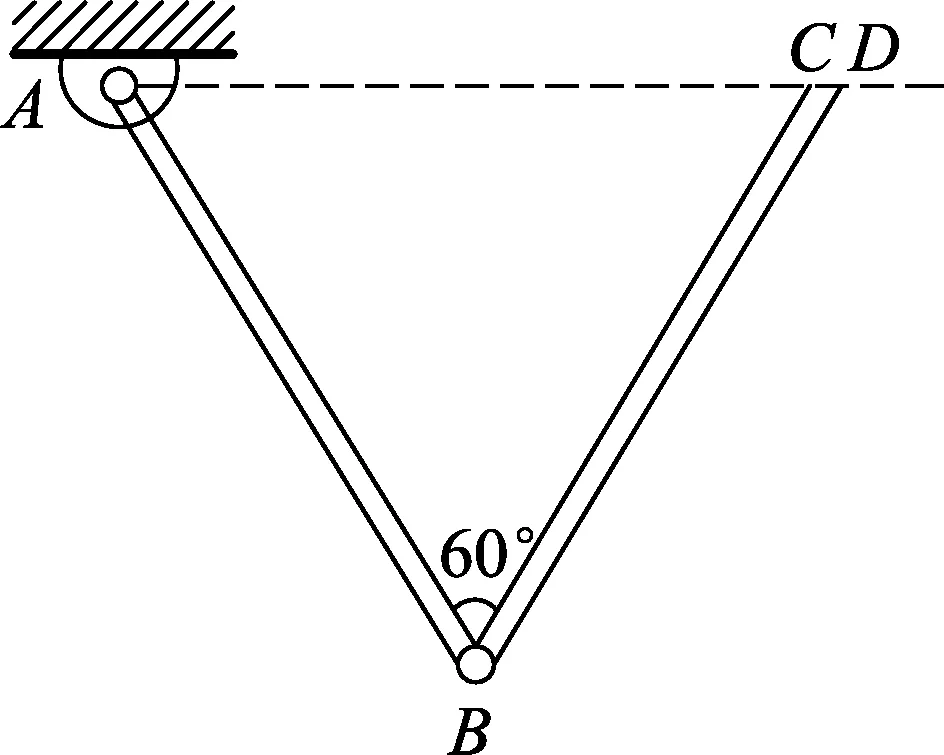
图5

题3.(第33届复赛)两根质量均匀分布的杆AB和BC,质量均为m,长均为l,A端被光滑铰接到一固定点(即AB杆可在竖直平面内绕A点无摩擦转动).开始时C点有外力保持两杆静止,A、C在同一水平线AD上,A、B、C3点都在同一竖直平面内,∠ABC=60°.某时刻撤去外力后两杆始终在竖直平面内运动．

(1) 若两杆在B点固结在一起,求

(i) 初始时两杆的角加速度;

(ii) 当AB杆运动到与水平线AD的夹角为θ时,AB杆绕A点转动的角速度.

(2) 若两杆在B点光滑铰接在一起(即BC杆可在竖直平面内绕B点无摩擦转动),求初始时两杆的角加速度以及两杆间的相互作用力.

解析: (1) (i) 设两杆的角加速度为α,两杆绕A点做定轴转动,由刚体转动定理得

(1)

由(1)式得

(2)

(ii) 系统势能的减少量为

(3)

系统动能的增加量为

可以将激励与考核机制设置为：按应收账款账龄或者应收账款逾期天数为标准来计算，把账龄分为不同的区间，再结合公司应收账款金额的具体情况和公司薪酬的状况来设计相应的比例，在不同的区间按不同的比例扣除薪酬。该措施是为了引导与应收账款管理相关的部门正确合理运用信用管理，将信用额度控制在合理范围内，从而降低企业发生坏账的风险，实现公司利益最大化。

(4)

整个过程机械能守恒

ΔEp减=ΔEk增.

(5)

由(3)～(5)式得

(6)

(2) 系统有2个自由度,以AB杆和BC杆与竖直方向的夹角θ1和θ2作为系统的广义坐标,设AB杆和BC杆的角加速度分别为α1和α2.建立以点A为原点,水平向右为x轴,竖直向下为y轴的坐标系,则BC杆的质心坐标为

(7)

(7)式对时间求导得质心速度

(8)

主动力是两杆的重力,是保守力.系统的动能为

(9)

系统的势能

(10)

拉格朗日函数

(11)

由拉格朗日方程得

(12)

(13)

(14)

设BC杆对AB杆的作用力沿x轴和y轴的分量分别为Fx、Fy.

对AB杆,相对于A点,由转动定理得

(15)

对BC杆,其绕质心转动,由转动定理得

(16)

两杆间相互作用力的大小为

(17)

联立(14)～(17)式得

(18)

BC杆对AB杆的作用力与竖直方向夹角φ满足

(19)

题4.(国家集训队)蒸汽机的飞球调速器,由两个质量为m的球通过4根长为l的铰臂,与套在竖直轴的上、下两个套筒连接而构成,上面的套筒固定,下面的套筒质量为M,可沿轴无摩擦地上、下滑动,如图6所示.整个装置绕竖直轴以恒定角速度ω0匀速转动,忽略各铰臂的质量及套筒M的转动惯量.

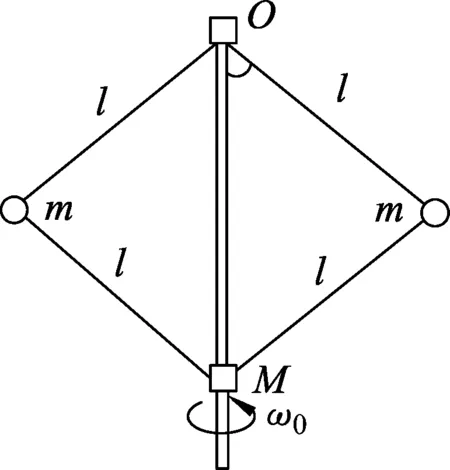
图6

(1) 求套筒M平衡时与上套筒之间的距离；

(2) 求套筒M在平衡位置附近上、下小振动的频率.

解析: (1) 设套筒M平衡时,在以角速度ω0绕轴旋转的转动参考系中,其中一个小球m的受力如图7所示,其中惯性离心力fi=mω02lsinθ,则有

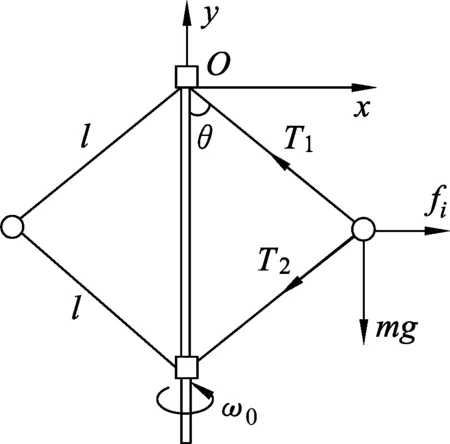
图7

(T1-T2)cosθ=mg.

(1)

(T1+T2)sinθ=fi=mω02lsinθ.

(2)

2T2cosθ=Mg.

(3)

由(1)～(3)式得

(4)

上下套筒距离

(5)

当然θ=0也是体系的一个可能平衡状态,此情况下L=2l.

(2) 系统有1个自由度,以上臂与竖直方向的夹角θ作为系统的广义坐标,系统动能为

(6)

系统势能:

V=-2(m+M)glcosθ.

(7)

拉格朗日函数:

L=T-V.

(8)

由拉格朗日方程得

(9)

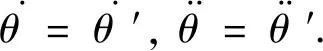
(m+M)gsinθ=0.

(10)

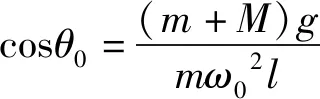
(11)

故小振动的频率为

(12)

总结:其实还有不少的竞赛题都能用拉格朗日方程求解,比如:第26届复赛第8题,第30届复赛第1题,第32届决赛第1题等,读者可以尝试求解并归类.