托卡马克等离子体中共振磁扰动场放大效应对离子轨道特性的作用*

苏春燕 牟茂淋† 陈少永 郭文平 唐昌建

1) (四川大学物理学院, 成都 610065)

2) (四川大学, 高能量密度物理及技术教育部重点实验室, 成都 610065)

首先, 利用MARS-F 程序模拟了HL-2A 装置中不同电阻率、环向旋转频率和环向模数条件下等离子体对共振磁扰动(RMP)的线性响应过程, 分析了不同情况下共振场放大效应对三维扰动磁场的影响; 然后, 利用Boris 算法追踪了三维场作用下的离子轨道, 并详细探究了不同扰动磁场改变离子轨道特性的物理机制.研究发现, 考虑等离子体响应后的扰动磁场可增强离子轨道径向展宽, 且轨道最大径向展宽随轨道上扰动磁场平均值的增大而增大; 同时, 离子在通过扰动磁场被强烈放大的区域时轨道径向展宽会显著增加.该物理机制可用于解释RMP 缓解边界局域模实验中离子直接损失增加和等离子体径向输运增强现象.

1 引 言

未来大型托卡马克聚变实验装置, 如中国聚变工程实验堆[1]、国际热核聚变实验堆[2]都将设计在高约束模式下运行.但是, 托卡马克高约束模式运行时常伴随着一种使边缘输运垒周期性地崩塌和重建, 同时快速释放热流和粒子流的不稳定现象,即边界局域模(edge localized mode, ELM)[3].未来聚变堆中I 型ELM 的爆发不仅会引发大量的粒子和能量损失, 同时还会对装置偏滤器靶板和第一壁造成极大损害.因此, 对ELM 的有效控制是未来托卡马克长时间稳定运行亟待解决的问题.

共振磁扰动(resonant magnetic perturbation,RMP)是目前已被证实的可有效控制ELM 的一种重要方法[4−7].RMP 由加在等离子体外部的磁扰动线圈产生, 由于RMP 的作用, 托卡马克中磁场的环向对称性将被破坏, 形成新的三维平衡.DIIID[8,9], KSTAR[10], ASDEX Upgrade[11]和MAST[12]等装置上的实验研究表明, 受三维共振磁扰动影响, 离子损失率会有所提升.为理解RMP 粒子约束物理, 最直接的方法就是在相关装置中模拟RMP作用下的粒子轨道: 一是简单将真空近似RMP 场叠加到平衡场中, 然后计算叠加磁场中的粒子轨道[13,14], 该方法的优点是计算过程简单, 可以定性给出RMP 对粒子约束的影响; 二是考虑RMP 场与等离子体的响应过程, 将等离子体响应后的扰动磁场与平衡磁场叠加再计算离子轨道, 由于此方法与真实物理过程更为接近, 所以得到的离子损失率与实验数据符合更好[10,15].

等离子体对RMP 的响应结果主要包含两种效应, 一是扰动磁场屏蔽效应(shielding effect)[16],即扰动磁场的共振分量在共振面上激发的感应电流产生的磁场与外加扰动磁场相抵消, 使得共振面上的总径向场减小的现象; 二是共振场放大效应[17,18], 即扰动磁场的非共振分量激发的近稳定模式产生的扰动电流, 使得非共振面上的总径向场增大的现象.已有代码如IPEC[19], MARS-F[20−22]等对不同装置中不同条件下等离子体对RMP 的线性响应过程都进行了较多模拟, 并且得到了与实验符合较好的模拟结果.但目前利用等离子体响应后的扰动磁场计算粒子轨道的研究还相对较少, 并没有系统给出RMP 响应场影响粒子约束的物理机理.为了更好地理解RMP 在粒子约束中的作用,有必要对不同条件下的RMP 响应场及其对离子轨道的影响进行全面分析.因此, 本文以HL-2A托卡马克装置第29676 炮放电820 ms 的平衡为基础, 计算了不同电阻率、环向旋转频率以及环向模数条件下考虑等离子体响应作用的RMP 场分布,分析了其对离子运动轨道产生的影响, 并得出了扰动磁场影响离子轨道的物理机理.

本文内容安排如下.第二部分介绍了模拟等离子体对RMP 的线性响应过程和离子轨道追踪使用的物理模型及文中使用的托卡马克平衡参数, 第三部分对比了不同参数条件下考虑等离子体响应后的扰动磁场分布, 计算了不同三维扰动磁场作用下的离子轨道, 并详细分析了轨道展宽机制.最后,第四部分对本文工作进行了总结.

2 物理模型及平衡

2.1 RMP 响应场物理模型

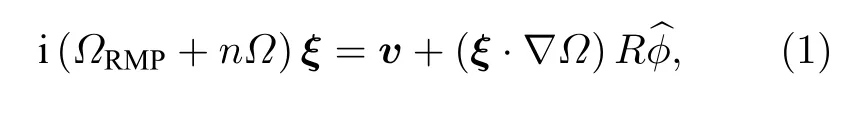
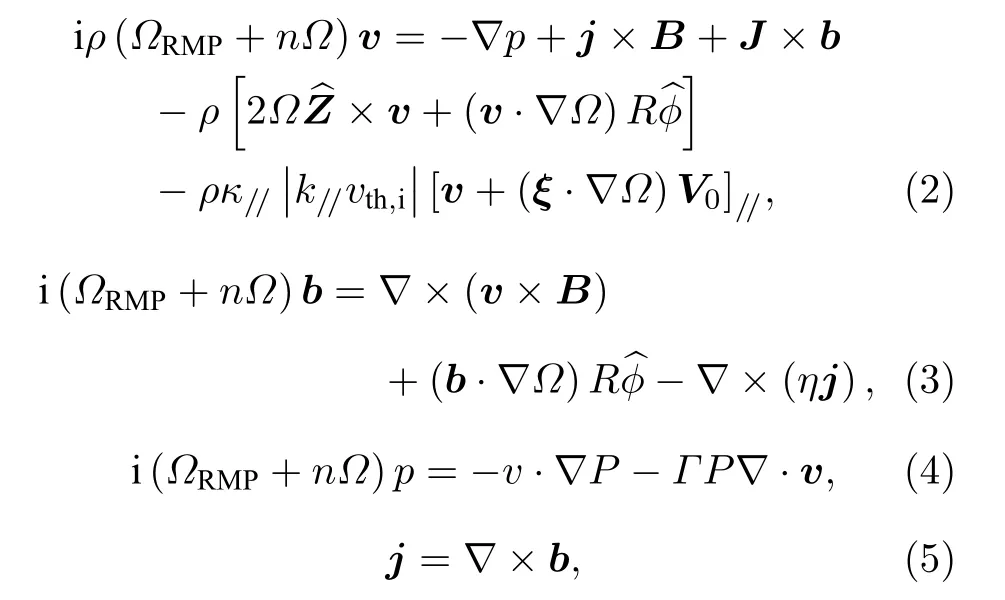
方程组中B,J,P和ρ为等离子体平衡量, 分别表示平衡的磁场、电流密度、压强和等离子体密度;ξ,v,b,j和p为等离子体扰动量, 分别表示扰动的位移、速度、磁场、电流密度和压强.此外,ΩRMP表示RMP 旋转频率, 本文考虑静态RMP 的作用,故ΩRMP=0.n是环向模数, 对于轴对称平衡中的线性等离子体响应, 仅考虑单一环向模数;R是等离子体大半经,是几何环向角φ的单位矢量,是极向截面内竖直方向的单位矢量, 等离子体环向流速方程(2)中最后一项代表平行声波阻尼效应[16],κ//为阻尼系数, 模拟中选取κ//=1.5 ,表示强声波阻尼.已有研究[24]表明, 对于低β等离子体, 声波阻尼效应并不会影响等离子体响应结果;对于高β等离子体, 考虑强声波阻尼的等离子体响应结果与实验更为接近.k//=(n −m/q)/R是平行波数, 其中m是极向模数,q是安全因子;vth,i=是热离子速度,Ti和Mi分别是热离子的温度和质量,η为等离子体电阻率,Γ= 5/3 表示绝热系数.此方程组中的所有量均为无量纲量, 其中磁场、位移、速度、压强和时间的无量纲因子分别为和τA, 此处,B0和R0分别为磁轴处的环向磁场和大半经,为环向Alfvén 速度,µ0为真 空磁 导率,τA=R0/vA为Alfvén 时间.

在MARS-F 中, RMP 线圈电流jRMP被看作是固定在某一径向位置的表面电流, 其环向分量沿环向角φ的变化为 e xp(inφ) , 极向分量通过电流无散条件计算得到, 满足方程

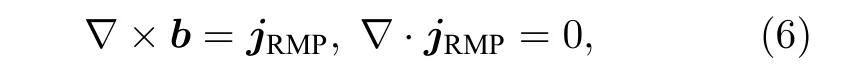
同时, 在真空区域扰动磁场满足

2.2 离子轨道计算模型

模拟中计算离子轨道的基本方程为牛顿运动方程, 利用Boris 算法[25−27]可以求解得到不同初始条件下的离子运动轨道, 该算法的基本特点是相空间体积守恒, 故计算中可以保持系统能量守恒[27].假设第n步(tn=nΔt)离子相空间坐标为(rn,vn), 不考虑电场的作用, 则通过Boris 算法计算第n+1 步(tn+1= (n+1)Δt)离子相空间坐标(rn+1,vn+1)的运动方程为

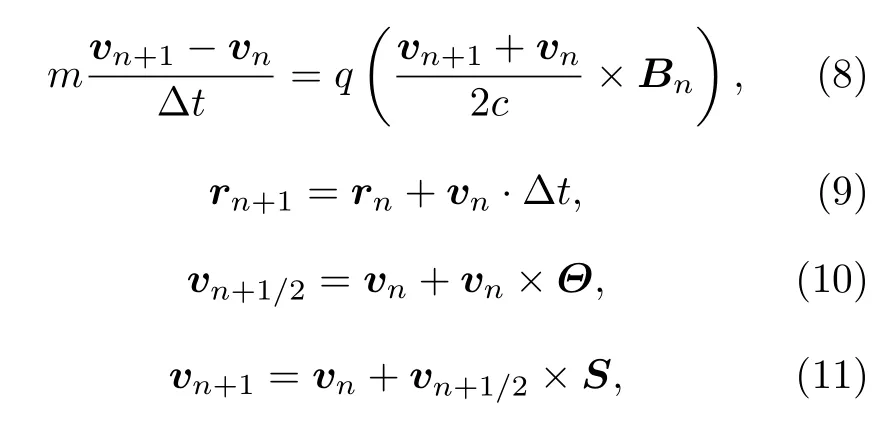
其中m和q分别为离子质量和电荷,c为光速, 磁场B为托卡马克平衡磁场和由MARS-F 计算的扰动磁场的总和.时间步长 Δt=T/k,T=2πmc/q|B|为离子回旋周期,k为每个回旋周期计算的步数,其取值将影响计算过程的磁矩误差, 本文取k=400000 , 磁矩误差范围在 1 0−3之内, 可以近似认为磁矩是守恒的.方程(10)中为 Δt/2 时间内速度变化的角度矢量, 其方向沿磁力线方向,vn+1/2表示洛伦兹力推动离子发生速度偏转过程中的中间速度矢量.方程(11)中vn+1/2×S表示离子在 Δt时间内的速度变化矢量,具体推导过程可以参考文献[28].

2.3 平衡参数

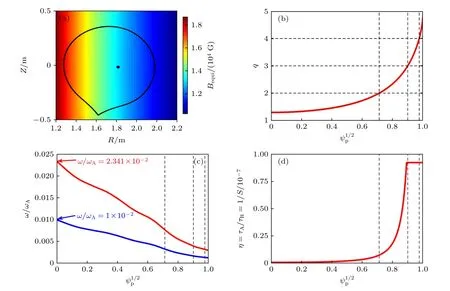
图1 HL-2A 第29676 炮放电的平衡参数分布(1 G = 10–4 T) (a)平衡磁场分布; (b)安全因子径向剖面; (c)归一化的等离子体环向旋转频率; (d)归一化电阻率; 黑色竖直虚线分别代表 q =2,3,4 的共振面位置Fig.1.Distribution of the plasma equilibrium parameters for HL-2A discharge 29676: (a) Equilibrium magnetic field; (b) safety factor; (c) plasma toroidal rotation, normalized to the Alfvén frequency at the plasma center; (d) normalized plasma resistivity.The vertical lines indicate the radial locations of resonant surfaces for q =2,3,4 , respectively.

文中所有计算均使用HL-2A 第29676 次放电的平衡参数, 通过EFIT[29]代码重构平衡并将其作为MARS-F 代码的平衡输入.图1(a)给出了平衡磁场的分布情况, 其中磁轴处磁感应强度B0=1.365 T , 大半径R0= 1.65 m , 小半径a=0.4 m ,归一化比压βN=2.1.图1(b)为MARS-F 代码中输出的安全因子剖面, 其芯部安全因子qmin=1.29 ,边缘安全因子q95=3.60 , 图中黑色竖直虚线分别对应q=2,3,4 的有理面位置.定义归一化极向磁通为ψp=(ψ −ψaxis)/(ψedge−ψaxis) , 这里ψaxis和ψedge分别表示磁轴和最外闭合磁面(last closed flux surface, LCFS)处的极向磁通, 图中横坐标取为ψp1/2代表曲线坐标系中的平衡通量面[16].图1(c)为等离子体环向旋转频率径向剖面, 该剖面是通过对实验数据进行拟合得到的, 其芯部归一化旋转频率ω0/ωA可根据模拟需要调整, 其中ωA=2.860×106Hz 为Alfvén 频率.由于在环向旋转频率较低时等离子体响应受电阻率影响较大[30], 为了减小电阻率对模拟结果的影响, 模拟选取的环向旋转频率(ω0/ωA=2.341×10−2, 图1(c)中红线)略大于实验结果; 此外, 文中还选取了与实验结果更为接近的环向旋转频率(ω0/ωA=1×10−2, 图1(c)中蓝线)进行对比分析.图1(d)为归一化电阻率η的径向剖面,η=1/S,S为伦奎斯特数, 模拟中采用斯必泽(Spitzer)电阻模型[22], 等离子体电阻率η=η1[Te/Te(0)]−3/2,Te是热电子温度,Te(0) 为磁轴处的热电子温度,η1=η0/(R0/a)2代表等离子体芯部电阻率幅值, 电阻率剖面由Te−3/2的剖面决定, 电阻率幅值可通过设置η0的值来确定.图1(d)为取η0=1.752×10−8时的电阻率剖面, 模拟区域对应的真实电阻率为9.032×10−9—9.004×10−7Ω·m.

3 模拟结果及分析

3.1 等离子体对RMP 的响应结果

HL-2A 中的RMP 线圈包含上下两组, 每组线圈包含两个环向对称的线圈, 每个线圈环向跨越11.4°, 安装在中平面窗口与上下窗口之间.线圈尺寸为420 mm × 260 mm, 电流大小为4.5 kA, 该RMP 线圈主要包含n= 1, 3, 5, 7 的环向分量, 对应电流幅值分别为0.284, 0.280, 0.273 和0.262 kA.已有研究[6]表明, 环向模数(n)越大, 其扰动磁场的极向谐波分量幅值随极向模数(m)增大在径向衰减越快, 故本文仅讨论等离子体对n=1 和 3 的扰动电流分量产生的扰动磁场的响应及其对离子轨道的影响.表1 是模拟中计算RMP 响应场的4 个不同算例, 分别选取了不同环向模数、等离子体旋转频率和电阻率.

图2 给出了不同参数情况下, 等离子体响应前(蓝线)、后(红线)扰动磁场的各极向谐波分量的径向剖面.在托卡马克中, 平衡磁场的径向分量几乎为零, 而扰动线圈产生的磁场主要为径向磁场, 所以可通过总径向磁场的变化来反映等离子体对RMP 的响应结果[31].在理想等离子体响应(图2(a))情况下, 共振面上的响应场被完全屏蔽,同时非共振面上的放大效应最大; 在电阻等离子体响应(图2(b))中, 响应场在q=3,4 共振面上并未被完全屏蔽, 且非共振面上的响应场幅值减小, 这是因为电阻使得感应产生的扰动电流发生耗散, 从而削弱了感应电流在非共振面上产生的扰动磁场;若减小电阻等离子体的环向旋转频率(图2(c)), 则q=3,4共振面上的屏蔽效应进一步减弱, 而非共振面上的响应场幅值略有增大, 这与文献[30]中的模拟结果一致; 取环向模数n=3 时, 扰动磁场的所有极向谐波分量在共振面上几乎都被完全屏蔽,且放大效应较弱, 其幅值在径向迅速衰减.

随着互联网技术和信息技术的不断发展，远程教学、网络在线教学等教学模式如雨后春笋，而相应的自主学习、协作学习等学习模式也在不断创新，从而为成人学习者学习方式的转变提供了可能。传统成人学习者通常是教师教什么学什么，教师要求学什么就学什么，是一种被动的接受的甚至是强迫式的学习，而随着成人教育者越发考虑到成人学生的具体要求和实际情况即学习时间有限学习目的强等因素，成人教育目前也多以远程教学和网络教学为主，这就要求学生有较高的自主学习能力，能严格按照教师的要求自主完成教学任务[4]。除了完成教师在网络上布置的具体任务之外，学习者还应根据自己的实际需求自主学习某些知识和技能。

表1 不同算例的等离子参数Table 1.Plasma parameters of different calculation cases.

图3 对比了无扰动磁场、加入真空近似RMP场和考虑不同情况(Case 1—Case 4)下等离子体响应后的扰动磁场的庞加莱图, 图中红点分别代表q=2,3,4的共振面位置.图3(a)平衡场中没有扰动磁场作用, 等离子体磁场分布没有出现磁岛结构; 但在图3(b)中, 真空近似RMP 场的存在导致等离子体在q=2,3,4 的共振面上出现较大的磁岛结构; 在考虑理想等离子响应时, 如图3(c)所示,由于共振面上的RMP 场被完全屏蔽, 所以磁岛结构消失; 而考虑电阻效应的非理想等离子情况(图3(d))中q=3,4 共振面上扰动磁场的屏蔽效应减弱, 故在q=3,4 共振面上有较窄的磁岛结构;当旋转频率降低时,q=3,4 共振面上等离子体对扰动磁场的屏蔽效应进一步减弱, 故图3(e)中q=3,4 共振面上磁岛结构大于图3(d); 在n=3 情况下(图3(f)), 共振面上的扰动磁场被完全屏蔽,故磁场庞加莱图中没有磁岛结构存在.

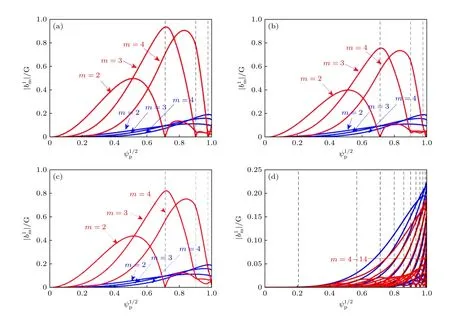
图2 Case 1—Case 4 情况下, 真空RMP 磁场(蓝线)和等离子体响应后总扰动磁场(红线)各极向谐波分量的径向剖面, 黑色虚线代表共振面位置Fig.2.Comparison of radial profiles between the vacuum (blue lines) and plasma response (red lines) RMP fields for the resonant poloidal Fourier harmonics in Case 1–Case 4.The dashed vertical lines indicate the radial locations of resonant surfaces.

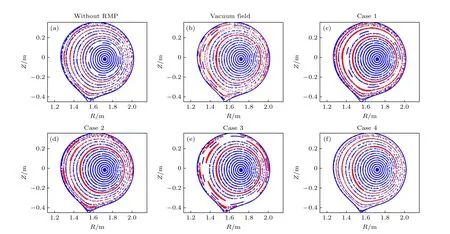
图3 在(a)平衡场、(b)真空近似RMP 场、(c)−(f) Case1−Case 4 等离子体响应扰动磁场作用下的R-Z 平面磁场庞加莱图(图中红点分别代表 q =2,3,4 的共振面位置)Fig.3.Poincare plots of magnetic field configuration on the R-Z plane for (a) unperturbed field, (b) vacuum RMP field and (c)–(f) plasma response RMP field for Case 1–Case 4.The red dots represent q =2,3,4 resonant surfaces.

图4 (a)真空近似RMP 场、(b)−(e) Case 1−Case 4 情况下等离子体响应后的总扰动磁场幅值在 φ =0 小截面的分布; 其中黑色实线代表最外闭合磁面位置, 黑色虚线分别代表 q =2,3,4 的共振面位置, 黑色实心点代表磁轴位置,最外闭合磁面外的两个强磁场区域代表RMP 线圈位置, 图4(b)中红色箭头处为共振场强放大区域Fig.4.Contour plots of peak amplitudes of the perturbed field due to (a) vacuum RMP and (b)–(e) plasma response RMP fields for Case 1–Case 4 in cross section with φ =0 , respectively.The black solid line is the LCFS, the black dashed lines are the positions of q =2,3,4 resonant surfaces, the black point represents the position of the magnetic axis.The two strong magnetic field regions outside the LCFS represent the positions of RMP coils.The areas pointed by red arrows in Fig.4(b) are the regions with strong field amplification.

图4 给出了真空近似RMP 场和Case 1—Case 4 四种情况下等离子体响应后的总扰动磁场幅值在φ=0 小截面的分布, 图中的扰动磁场包含了所有极向谐波分量.真空近似RMP 场(图4(a))在等离子体区域的扰动磁场分布随到RMP 线圈的距离增加而迅速减小; 相比之下, 理想等离子体响应(图4(b))时, 共振场放大效应使等离子体区域的扰动磁场明显增强, 且在共振面附近具有更复杂的磁场结构, 尤其在q=2 共振面内侧(图4(b)中红色箭头处)可以看到两个明显的扰动磁场增强区域; 当等离子电阻率不为零(η0=1.7524×10−8)时, 如图4(c)所示, 由于共振场放大效应减弱, 扰动磁场强度整体较图4(b)减小; 对比图4(c)和图4(d)发现, 当减小电阻等离子体环向旋转时, 扰动磁场的整体幅值变化不大, 但是由于旋转频率减小导致的放大与屏蔽效应变化相反, 所以扰动磁场的分布呈现出强场侧增强, 弱场侧减弱的现象, 说明放大效应在强场侧占主导, 而在弱场侧由于屏蔽效应减弱, 放大效应也会受到一定影响.对比图4(c)和图4(e), 由于n=3 的扰动磁场放大效应较弱且径向衰减较强, 所以其响应后的总扰动磁场明显小于n=1 的情况.

3.2 RMP 作用下的离子轨道分析

在HL-2A 实验中, 中性束注入粒子的能量一般为几十keV, 所以本文选取初始能量E0=30 keV的离子(质子), 对其在不同扰动磁场作用下的轨道进行详细分析.首先, 考虑无扰动磁场作用时分别从外中平面上q=2,3,4 有理面出发的基本离子轨道.如图5 所示, 3 0 keV 的质子在HL-2A 中具有较大的漂移, 这将导致正向入射(v>0 )的离子很快漂离LCFS, 如初始位置为q=3,4 的离子; 而反向入射(v<0 )的离子则很容易漂移到离初始磁面较远的磁面上, 如初始位置为q=3,4 的通行离子很容易漂移到q=2 的有理面附近.为了更有针对性地分析RMP 响应场对离子轨道的影响, 文中轨道追踪全部考虑反向入射情况.图6 给出了在Case 1—Case 4 的扰动磁场作用下, 从外中平面上q=2有理面出发反向入射的典型通行(红线)和捕获(蓝线)轨道.相比于相同条件平衡场中的反向入射轨道(图5(a)), 响应场作用下的轨道变“粗”,即产生轨道径向展宽, 该现象在Case 1 和Case 2中尤为明显.

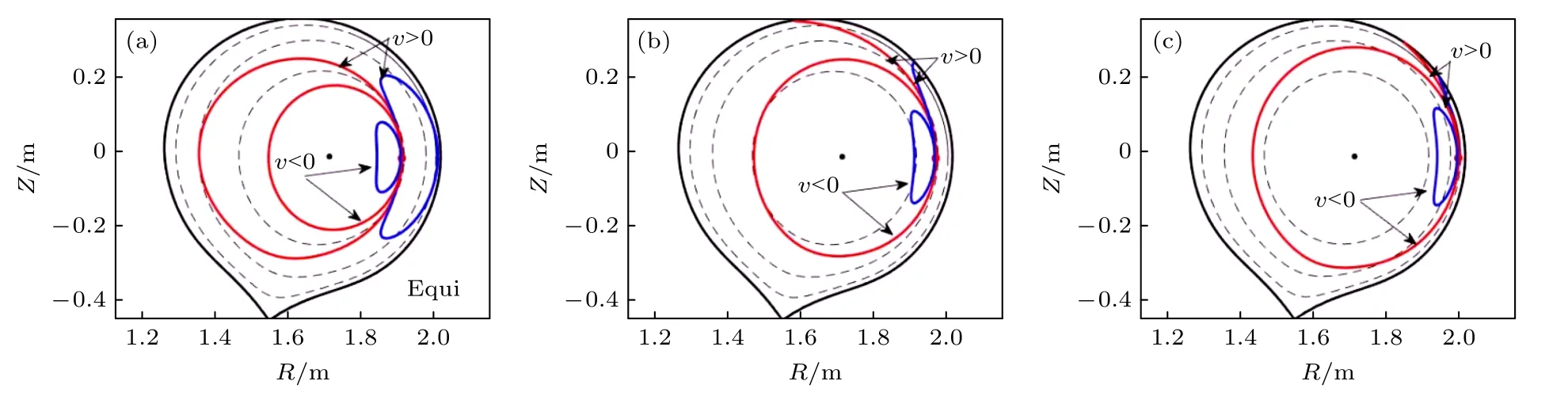
图5 无扰动磁场作用时, 分别从外中平面上q = (a) 2, (b) 3, (c) 4 共振面(黑色虚线)出发的基本离子轨道, 其中红线代表通行轨道, 蓝线代表捕获轨道Fig.5.Fundamental ion orbits with unperturbed magnetic fields which launched from (a) q =2 , (b) q =3 , (c) q =4 resonant surfaces, respectively.The red lines represent passing orbits, and the blue lines represent trapped orbits.

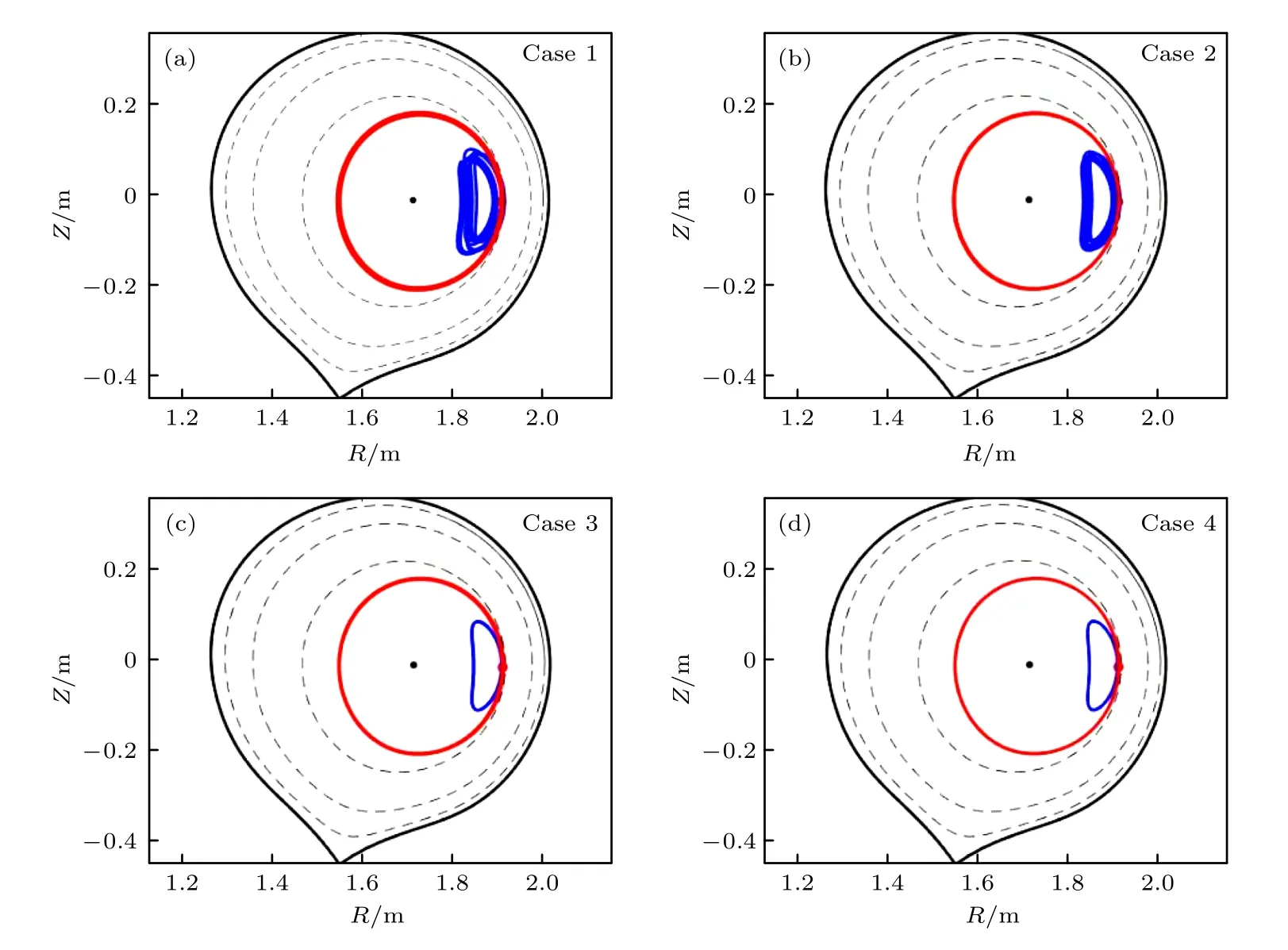
图6 在Case 1—Case 4 的扰动磁场作用下, 从外中平面上 q =2 共振面出发反向入射的典型通行(红线)和捕获(蓝线)轨道(黑色虚线分别代表 q =2,3,4 的共振面位置)Fig.6.Typical ion orbits with Case 1–Case4 plasma response RMP field which launched from outer middle plane of q =2 resonant surface.The red lines represent passing orbits, and the blue lines represent trapped orbits.The black dashed lines are the positions of q =2,3,4 resonant surfaces.

利用轨道的极向磁通变化可以更加清楚地分析轨道特征, 由于轨道自身漂移, 离子极向磁通随时间呈周期性变化.对于本文研究的向内漂移反向入射轨道, 磁通波峰(波谷)通常对应中平面上外(内)侧轨道的磁面位置.若轨道磁通的波峰和波谷一直保持不变, 则轨道整体在径向没有出现周期性漂移, 无径向展宽; 若轨道磁通波峰或波谷出现变化, 则说明轨道整体发生了径向漂移.这里定义轨道磁通波峰(波谷)的最大值与最小值间的差值为ΔΨp( ΔΨv), 则离子轨道最大径向展宽 ΔΨmax取两者间的较大值, 即 ΔΨmax=max(ΔΨp,ΔΨv).

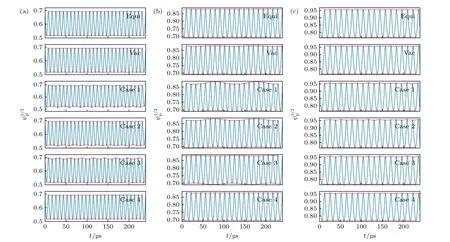
图7 不同扰动磁场作用下通行轨道极向磁通随时间的变化 (a)—(c)离子轨道初始位置分别为 q =2,3,4 的有理面, 离子初始能量E0 =30 keVFig.7.Variations of the poloidal flux for passing orbits launched from (a) q =2 , (b) q =3 , (c) q =4 resonant surfaces with different perturbation magnetic fields.The ion initial energy E 0 =30 keV.

图7 为不同扰动磁场作用下通行轨道极向磁通及随时间的变化.对于从q=2 面出发的通行离子, 如图7(a)所示, 在平衡场(Equi)作用下,ΔΨp=ΔΨv=0, 轨道无径向展宽; 在真空RMP 场(Vac)作用下, 由于真空RMP 场幅值较小, 轨道磁通变化规律与平衡场相似; 但在理想等离子体响应场(Case 1)作用下, 轨道磁通波峰和波谷都出现一定的周期性变化, 且 ΔΨp<ΔΨv, 离子轨道最大径向展宽 ΔΨmax=ΔΨv≈0.0095 ; 当考虑等离子的电阻效应(Case 2)时, 强场侧扰动磁场减小(图4(c)),离子轨道最大径向展宽减小为ΔΨmax=ΔΨv≈0.0078; 当减小电阻等离子体的环向旋转频率(Case 3)时, 由于强场侧扰动磁场增大(图4(d)),轨道磁通波峰变化增强, 离子轨道最大径向展宽又增加为 ΔΨmax=ΔΨp≈0.0094 ; 当环向模数n=3时, 轨道整体周期性漂移几乎消失, 近似有ΔΨp=ΔΨv=0.同理, 可得到q=3,4 面上的离子轨道展宽结果.分析可知, 理想等离子体响应场(Case 1)作用下的轨道展宽在不同有理面上始终最大; 而电阻等离子体响应(Case 2, Case 3)下的轨道展宽略小, 且会随旋转频率的变化而发生小幅改变; 此外,高环向模数的扰动磁场由于径向衰减迅速, 并不会使离子轨道产生径向展宽.

对于相同条件下的捕获轨道, 如图8 所示, 在q=2共振面上的捕获轨道, Case 1 理想等离子体响应场下的离子轨道出现明显漂移, 最大径向展宽ΔΨmax=ΔΨv≈0.13; 同时, Case 2 电阻等离子体响应场下的离子轨道最大径向展宽ΔΨmax=ΔΨv≈0.07; 但是, 在旋转频率减小时, Case 3 响应场下的捕获轨道几乎无径向展宽, 这是因为该捕获离子轨道小截面投影主要位于q=2 共振面以内的弱场侧, 而该区域的扰动磁场由于旋转频率变化而明显减小(如图4(d)所示), 故未能使轨道发生整体径向漂移; 对于Case 4, 由于高n模数的扰动磁场幅值很小, 所以其捕获轨道也无径向展宽.对于q=3,4共振面上的捕获轨道, 其轨道运动规律与q=2共振面上的结果相似, 但由于扰动磁场幅值的差异, 相应的最大径向展宽数值也有所不同.

为了理解上述轨道漂移结果, 分别计算了不同扰动磁场、不同初始位置离子轨道的最大径向展宽( ΔΨmax)及相应轨道上的扰动磁场平均值( δBavg).图9(a)为初始能量为E0=30 keV 的通行离子的结果, 可以看出, 不同初始位置出发的离子轨道最大径向展宽均随轨道上扰动磁场平均值的增加而增加.其中红、黑色虚线斜率相近, 而绿色虚线斜率最大, 说明从q=3 共振面出发的离子轨道展宽受扰动磁场影响最明显.由图10(a)可知,从q=3 共振面出发的离子更容易由于轨道漂移而进入图10(a)中红色箭头所指的强场侧两个扰动磁场明显增强的区域, 故离子轨道展宽除与轨道上的扰动磁场平均值相关外还和扰动磁场的分布相关.图9(b)为相应捕获离子的情况, 捕获离子的轨道最大径向展宽同样和轨道上的扰动磁场平均值线性相关, 但此时q=2 共振面出发(红色虚线)的离子轨道展宽受扰动磁场影响最大.由图10(b)可知, 从q=2 共振面出发的捕获离子轨道小截面投影主要位于图10(b)中蓝色箭头所指的弱场侧扰动磁场明显增强的区域, 故轨道最大径向展宽也显著增大.

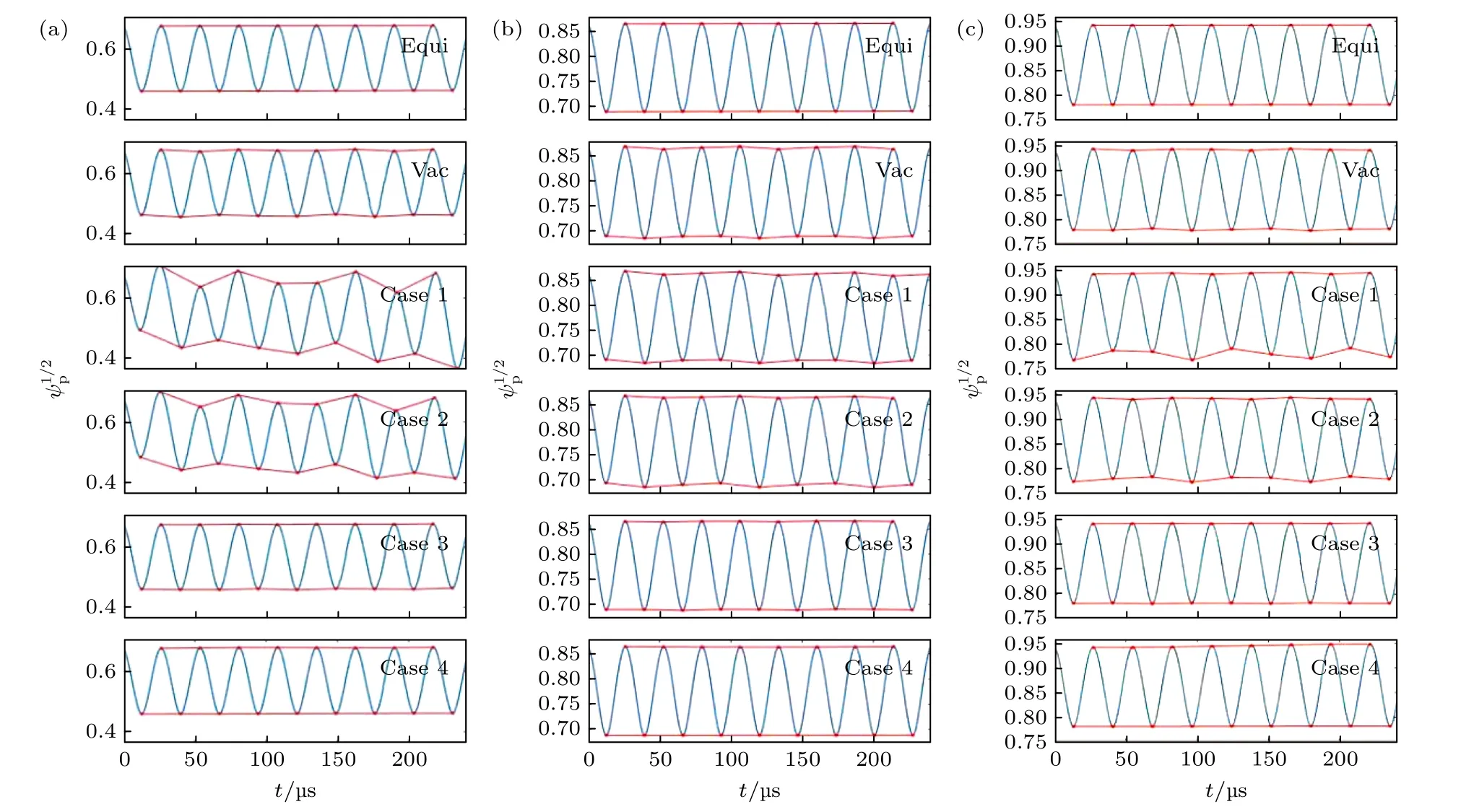
图8 不同扰动磁场作用下捕获轨道极向磁通 (a)—(c)离子轨道初始位置分别为 q =2,3,4 的有理面, 离子初始能量E0 =30keVFig.8.Variations of the poloidal flux for trapped orbits launched from (a) q =2 , (b) q =3 , (c) q =4 resonant surfaces with different perturbation magnetic fields.The ion initial energy E 0 =30 keV.

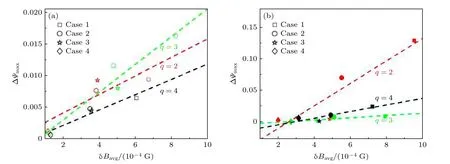
图9 初始能量 E 0 =30 keV 的通行(a)和捕获(b)离子轨道最大径向展宽( Δ Ψmax )随轨道上扰动磁场平均值( δ Bavg )的变化(图中正方形、圆形、五角星和菱形依次对应Case 1—Case 4 扰动磁场的情况, 红、绿、黑色图形分别表示初始位置为q =2,3,4共振面上轨道参量的计算结果, 红、绿、黑色虚线为对相同颜色图形进行数值拟合的结果)Fig.9.Variations of the maximum expansion distance ( Δ Ψmax ) and the average value of the orbital response field ( δ Bavg ) for(a) passing orbits and (b) trapped orbits with E 0 =30 keV.The square, circle, pentagram and diamond in the figure correspond to perturbation magnetic field in Case 1–Case 4, respectively.The red, green and black labels represent the calculation results for ions launched from q =2,3,4 resonant surfaces, respectively.The red, green and black dashed lines are the numerical fitting results of the same-colored labels.

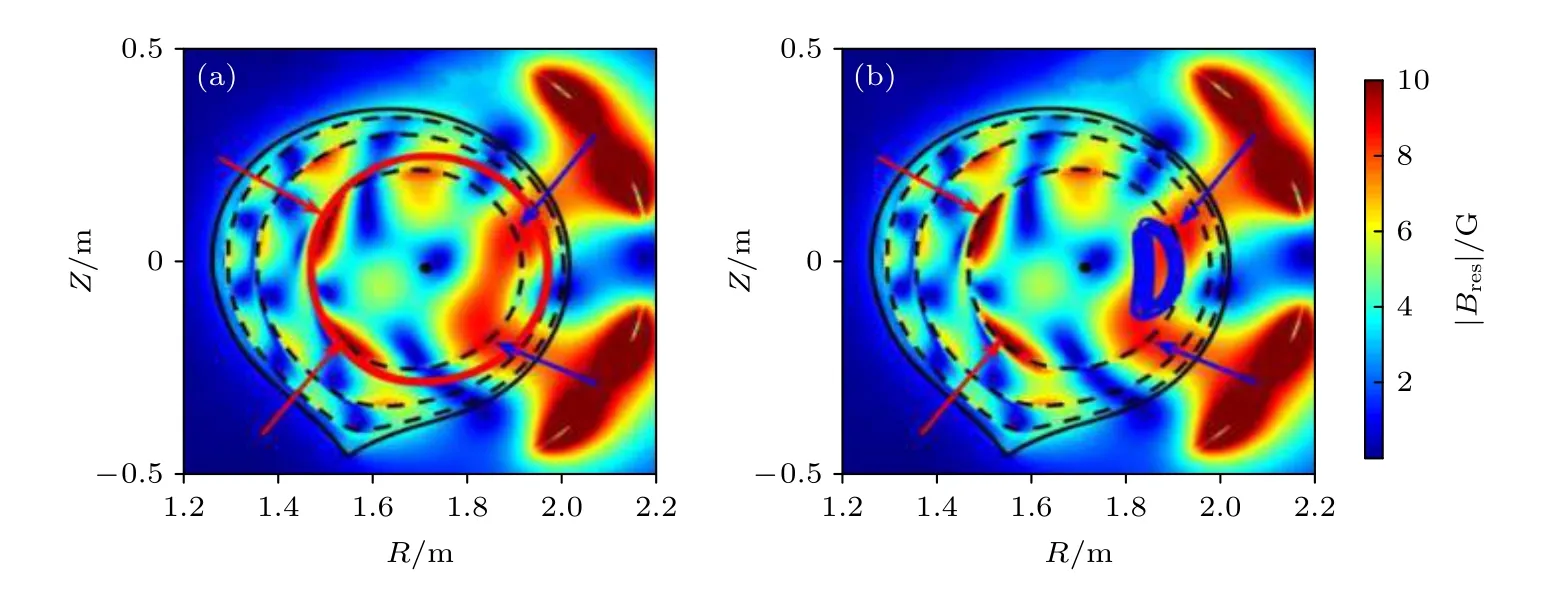
图10 理想等离子体响应场(Case 1)下, (a)从 q =3 共振面出发的通行离子轨道(红线), (b)从 q =2 共振面出发的捕获离子轨道(蓝线)(图中彩色背景为理想等离子体响应后的总扰动磁场在 φ =0 小截面的分布, 黑色实线代表最外闭合磁面位置, 黑色虚线分别代表 q =2,3,4 的共振面位置, 红(蓝)色箭头所指为强(弱)场侧两个扰动磁场明显增强的区域)Fig.10.Trajectory projection of ions orbit in ideal plasma response field (Case 1): (a) Passing orbit (red line) launched fromq =3 resonant surface; (b) trapped orbit (blue line) launched from q =2 resonant surface.The background is the distribution of plasma response RMP field in φ =0 cross section, and the black solid line is the LCFS, the black dashed lines are the positions of q = 2,3,4resonant surfaces.The areas pointed by the red (blue) arrows are two regions with the strong field amplification in high(low) field side.

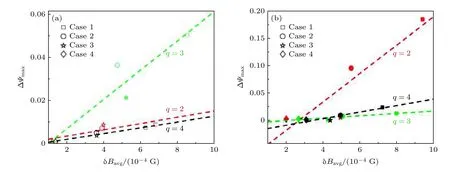
图11 初始能量为 E 0 =40 keV 的通行(a)和捕获(b)离子轨道最大径向展宽( Δ Ψmax )随轨道上扰动磁场平均值( δ Bavg )的变化(图中正方形、圆形、五角星和菱形依次对应Case 1—Case 4 扰动磁场的情况, 红、绿、黑色图形分别表示初始位置为q =2,3,4共振面上轨道参量的计算结果, 红、绿、黑色虚线为对相同颜色图形进行数值拟合的结果)Fig.11.Variations of the maximum expansion distance ( Δ Ψmax ) and the average value of the orbital response field ( δ Bavg ) for(a) passing orbits and (b) trapped orbits with E 0 =40 keV.The square, circle, pentagram and diamond in the figure correspond to perturbation magnetic field in Case 1–Case 4, respectively.The red, green and black labels represent the calculation results for ions launched from q =2,3,4 resonant surfaces, respectively.The red, green and black dashed lines are the numerical fitting results of the same-colored labels.

为了验证上述结果, 本文还计算了不同初始能量(E0=40 keV )条件下的轨道最大径向展宽随轨道上扰动磁场平均值的变化结果, 如图11 所示,E0=40 keV的通行和捕获离子的轨道展宽规律与E0=30 keV 的结果相似.但是, 从q=3 共振面出发的通行离子轨道最大径向展宽对应的绿色虚线斜率更大, 这是因为随着离子初始能量增加, 离子轨道的径向漂移也随之增加, 故相比于图10(a),从q=3 共振面出发E0=40 keV 的通行离子轨道将漂移到q=2 共振面内侧, 而此区域的扰动磁场更强, 所以其轨道最大径向展宽进一步增大.

4 结 论

本文基于HL-2A 平衡参数, 首先采用MARS-F程序模拟了等离子体对RMP 的响应过程, 得出等离子体响应后的三维扰动磁场结构, 然后利用Boris 算法追踪了三维扰动磁场作用下的离子轨道, 详细探究了不同电阻率、环向旋转频率和环向模数条件下的扰动磁场对离子轨道的影响规律及作用机制.研究发现, 由于等离子体对RMP 响应过程中的共振场放大效应使等离子体区域的扰动磁场幅值明显增加, 所以考虑等离子体响应后的扰动磁场可增强离子轨道径向展宽, 且最大径向展宽与轨道上的扰动磁场平均值和扰动磁场分布密切相关.具体表现为: 电阻率的增加会降低扰动磁场平均值而使轨道展宽减小, 等离子体旋转频率的变化会改变扰动磁场分布从而使不同种类的离子轨道展宽发生变化, 而环向模数的增加会导致响应后的扰动磁场幅值明显降低而对离子轨道几乎不产生影响.

虽然轨道最大径向展宽随轨道上扰动磁场平均值的增大而增大, 但是离子在通过扰动磁场被强烈放大(在HL-2A 中为q=2 有理面以内)的区域时, 轨道径向展宽才会显著增加.实验中, 如何让离子进入或者避开扰动磁场被强烈放大的区域, 对于提高等离子体约束性能十分重要.根据本文结果, 在HL-2A 实验中可以从两个方面控制离子轨道径向展宽: 一是通过控制等离子体参数降低扰动磁场被强烈放大区域内的扰动磁场幅值, 如增加等离子体电阻率、改变环向旋转频率、增加扰动磁场环向模数等; 二是通过控制离子初始位置及投射角避免离子运动到扰动磁场被强烈放大的区域内, 如对于切向注入的离子(通行轨道), 避免在q=3 有理面的径向位置注入, 对于垂直注入的离子(捕获轨道), 避免在q=2 有理面的径向位置注入.

等离子对RMP 的响应引起的离子轨道径向展宽, 一方面可能使离子直接损失增加而降低等离子体约束; 另一方面也可以增强等离子体径向输运, 为实验中的RMP 缓解ELM 现象提供可能的物理机理.目前, 本文工作仅针对单一离子轨道进行了模拟分析, 提出了RMP 改变扰动磁场影响离子约束的物理机理, 但进一步结合实验的应用还需要对多粒子系统进行模拟, 同时考虑粒子间的相互作用, 相关内容将在未来工作中继续完善.

感谢美国通用原子公司的刘钺强研究员在MARS-F程序和模拟工作中给予的指导和帮助.感谢核工业西南物理研究院提供的HL-2A 实验参数作为本文工作的基础.感谢东华大学的李莉、大连海事大学的周利娜、核工业西南物理研究院的王硕、吴娜、张能、陈海涛在MARS-F 程序调试过程中给予的帮助和支持.