一种面向不均衡数据集的CHI特征选择改进算法
2021-05-14骆魁永
骆魁永
(信阳农林学院 信息工程学院,河南 信阳 464000)
随着网络技术的快速发展,网络中各种文本信息以指数级的速度增长,文本分类[1,2]在信息检索、内容信息过滤、自然语言处理和信息组织与管理等领域应用越来越广泛.然而,在对海量电子文档的分类中,发现数据不均衡分布的情况普遍存在,在数据集中不同类别之间的文本数量可能存在数量级的差距,这给文本分类带来了新的挑战.面对这样的情况,特征选择作为文本分类的重要环节,传统的χ2特征选择方法在特征项选择的过程中往往会出现类别倾向的问题,导致分类器对稀有类别不能产生较好的分类效果.
目前,一些学者指出了χ2统计模型存在的缺点,并提出了相应的改进模型.文献[3]指出负相关特征项也会包含分类价值,正负相关特征项需要区别对待,通过对正负相关特征项赋予不同权重,改进了χ2统计模型;针对特征项在类间与类内分布的差异性对χ2统计模型的影响;文献[4]结合信息增益与文本频率方法的优点,提出了一种组合型模型,提高了χ2统计模型的性能;针对与类别正负相关的特征项对χ2统计模型的影响;文献[5]定义了频度、集中度和分散度的概念,并以此作为特征项的权重应用到新的模型中,使得改进后的模型倾向于选择高频、集中度高和分散度低的特征项;文献[6]提出了特征项与类别正负相关性的概念,并剔除与类别负相关的特征项,从而达到χ2统计模型的优化;文献[7]在χ2统计模型的基础上添加了三个调节参数,以此度量特征项对特定类别的分类价值,提出了一种基于方差的χ2统计模型.然而上述所有方法都没有考虑在不均衡数据集的类别间文档频数的差异性,针对上述存在的问题和不均衡数据集倾斜的特点,本文引入了类内词频概率因子、类间文档概率集中因子和类内均匀因子,对传统卡方统计模型进行改进,提出了一种改进的CHI特征选择方法,通过在复旦大学计算机信息与技术系整理的语料库中进行实验,实验结果表明该特征选择方法在不均衡数据集上分类效果比传统CHI要好,特别是在小类别中分类效果有明显的提高.
1 CHI特征选择算法及相关研究
1.1 CHI特征选择算法
χ2统计量可以用来度量特征tk和文档类别Ci之间的相关程度;假设特征tk(k=1,2,…,n)和文档类别Ci之间符合具有一阶自由度的χ2分布.假定训练文本集为S,其中有M个类别C1,C2,…Ci,…CM,S的总文档数为N,那么特征tk与类别Ci之间χ2统计量可以表示如式(1)所示.
(1)
式(1)中:A表示在类别Ci中且包含有特征项tk的文档数;B表示不在类别Ci中但包含有特征项tk的文档数;C表示在类别Ci但是不包含有特征项tk的文档数;D表示既不在类别Ci也不包含有特征项tk的文档数;N表示语料集中的样本总数.
对于全局特征选择,先按式(1)计算tk与每个类别Ci的χ2值,然后根据式(2)或式(3)计算特征tk对整个训练文本集的χ2统计值.最后根据χ2统计值的大小进行排序,在候选特征集中选择指定数目的特征项作为特征集.
(2)
(3)
特征项tk与类别Ci的相关性越强,χ2(tk,Ci)的值就越大,此时特征项tk对类别Ci来说,分类价值越多.
1.2 相关改进算法描述
Yang[8]在研究中指出,χ2统计特征选择算法是当前针对中文文本分类性能最好的特征选择算法之一,但算法依然存在很多不足.首先,一个有分类价值的特征词,应该在指定类各文档中均匀地出现,若只集中出现在该类的个别文档中,而在其他文档中很少出现,则对该类别来说,该特征项具有的类别鉴别信息要少很多;其次,χ2统计模型很容易把对特定类别贡献低而对其他类别贡献高的特征项选择出来;最后,传统χ2统计模型只考虑了特征项在所有文档中出现的次数,并不考虑特征项在某一文档中出现的次数,存在倾向低频词的缺点.
针对以上的问题,文献[7],在χ2模型的基础上引入3个调节参数作为特征项的影响权重,提出了一种基于方差的χ2特征选择方法.公式表示如式(4)所示:
(4)
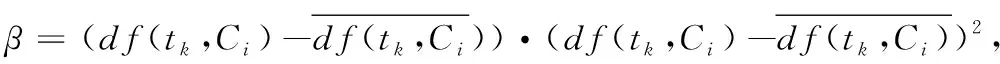
文献[6]针对χ2统计特征选择算法对类别负相关和正相关的特征项平等对待的问题,对传统χ2统计方法做了一定的改进,将那些与类别表现负相关的特征项剔除,从而忽略了与类别负相关对χ2统计模型的影响,改进后的模型表示如式(5):
(5)
文献[3]指出仅考虑特征项与类别的正相关性,完全忽略与类别表现为负相关的特征项具有一定不合理性,对于小类来说,与类别负相关的特征项依然含有一定的鉴别信息.因此文献[9,10]在χ2模型的基础上,加入了倾向因子α,改进后模型如式(6)所示:
(6)
2 改进的CHI特征选择算法
2.1 加入类内词频概率因子
χ2统计模型只考虑了特征项在所有文档出现的次数,而没有考虑特征项在指定类中出现的次数.即χ2统计模型只考虑了特征项的文档频数,没有考虑特征项在指定类中的词频,从而放大了低频词对指定类别的分类价值.
基于客观事实,一个有分类价值的特征词,应该在指定类文档中出现的次数较多.因此文献[7]将特征项在指定类中各文档出现的总次数作为χ2统计模型的调节参数,其中调节参数α如式(7):
α(tk,Ci)=tf(tk,Ci)
(7)
但是在不均衡数据集中,由于各类别之间文档频数差异比较大,单纯的以词频来度量特征项的频繁程度,算法往往会更倾向于选择大类的特征项,这对稀有类别是不公平的,降低了稀有类别的分类效果.
例如:假设在一个小类别Cp有200篇文档,特征词ts在类别Cs中出现的总次数为50;而在另一个大类别Cq中有1000篇文档,特征词tt在类别Cq中出现的总次数为100,那么明显α(tk,Cp)<α(tk,Cq),但是实际上,特征词ts对于类别Cp的重要性是高于特征词tt对于类别Cq的重要性的,导致模型倾向于选择对大类有分类价值的特征项,减少了对稀有类别有分类价值的特征项,从而降低了小类别分类的准确性.
为了避免对大类的特征项的这种选择倾向性,本文以类内的特征项在文档中概率信息来度量特征项在不平衡数据集的频繁程度,引入了类内词频概率因子αnew,表示如式(8)所示:
(8)

类内词频概率因子αnew(tk,Ci)表示在类别Ci中特征项tk的词频概率,度量了在不平衡数据集下特征项tk在类别Ci出现的频繁程度.αnew(tk,Ci)值越大,表示该特征项在该类中出现的频率较高,表明该特征项对该类具有强类别区分能力;αnew(tk,Ci)值越低,表示该特征项在该类中出现的频率较低,表明该特征项对该类具有弱类别区分能力.
2.2 加入类间文档概率集中因子
χ2统计模型是一种双边准则的特征选择模型,即该模型没有区分与类别正负相关的特征项对指定类别的重要程度,使得选择出来的特征项对特定类别贡献低而对其他类别贡献高[3].一个有分类价值的特征项,应该在指定类文档中出现的次数较多,在其他类文档中出现次数较少.文献[7]以文档频数为基础,根据方差的思想度量了特征项在类间的集中程度,并引入了参数β,其中β如式(9)所示.
(9)
分析式(9)可知,与类别负相关的特征项,其β(tk,Ci)值为负值,在模型选择中会被忽略,从而消除了与类别负相关的特征项对模型选择的影响.但是在不平衡数据集中,上述方法都没有考虑各类别之间文档频数的差异性,以文档频数为基础度量特征项在各类间的集中程度,在不平衡数据集中并不能适用,同样存在倾向于选择大类特征项的问题.
假设现在有两个类别,一个小类别Cp有200篇文档,大类别Cq有1000篇文档,其中小类别Cp含有特征词ts的文档数有199篇,大类别Cq含有特征词ts的文档数有10篇,小类别Cp含有特征词tt的文档数有10篇,大类别Cq含有特征词ts的文档数有101篇,那么明显α(ts,Cp)<α(tt,Cq),算法会选择tt做特征项,但是对比很容易发现,特征词ts几乎在类别Cp中的全部文档出现,而特征词tt虽然出现在类别Cq的文档频数比特征词ts出现在类别Cp的文档频数大,但出现的文档数只占类别Cq的总体文档的一小部分,因此特征词ts对于类别Cp的分类价值是高于特征词tt对于类别Cq的分类价值.
因此,为了解决类别倾向性问题,以及忽略了负相关对特征选择的影响的问题,本文以类内中包含特征项tk的文档概率来度量特征项在不平衡数据集中类间的集中程度,并考虑了负相关特征项的对稀有类别的价值,添加了类别倾向因子θ,并对β进行了修正和完善,得到了类间文档概率集中因子βnew,如式(10)所示:
(10)
式(10)中:M表示类别总数;df(tk,Ci)表示类别Ci中含有特征项tk的文档频数;df(Ci)表示类别Ci中的文档频数;A表示在类别Ci中含有特征项tk的文档数;B表示不在类别Ci中但包含特征项tk的文档数;C表示在类别Ci但是不包含有特征项tk的文档数;D表示既不在类别Ci中也不包含有特征项tk的文档数;当AD-BC<0且θ>0.5时,表示A相对D来说较多,造成负相关的主要原因是D较少,在实际应用中,小类发生这样的可能性往往大于大类,所以θ是一个倾向于小类的选择的因子.
类间文档频率集中因子βnew(tk,Ci)表示类别Ci中含有特征项tk的文档频率与所有类中还有该特征项的文档频率的平均值的偏离程度,度量了在不均衡数据集中特征项tk在类别Ci出现的集中程度.βnew(tk,Ci)值越大,表示该特征项在该类中的文档中出现的概率越高,而在其它类中的文档中出现的频率越低,显然该特征项对该类具有高的分类价值.
2.3 加入类内均匀因子
χ2统计模型没有考虑特征项在类内各文档的分布情况.一般来说,对特定类别具有鉴别能力的特征项,应该在指定类中各文档中均匀地出现,若只集中在该类的个别文档中出现,而在其它文档中很少出现,则表明特征项对该类别的鉴别信息就要小很多.
考虑下面的情况,假设特征项tk在类别Ci中,仅在少数几个文档中出现,即使出现频数比较大,该特征项对该类别也不具有很高的分类价值.因此,特征项在某一类中各个文档中分布越均匀,其类别表现能力越强.
根据样本方差的思想,特征项在该类各个文档出现频数越接近,说明该特征项在该类各文档中分布越均匀,总体方差就越小,其类别表现能力越强.反之,样本方差越大,其类别表现能力越低.
对文献[7]中的γ参数进行修正和变型,可以得到特征项类内平衡因子γnew,如式(11)所示:
(11)
式(11)中:Mi表示类别Ci中的文档数;tf(tk,dij)表示特征词tk在类别Ci中的文档dij中出现的次数.
γnew(tk,Ci)度量的是特征项tk在类别Ci中各文档的分布均匀程度,显然特征项tk在类Ci各个文档之间的分布越平均,γnew(tk,Ci)的值越大,该特征项对该类的鉴别价值就越高.
综上可知,在不平衡数据集中,其类内词频概率因子、类间文档概率集中因子和类内平衡因子都有很大的特征项,该特征项对该类的类别辨识能力越强.因此对传统χ2统计模型改进后如式(12)所示:
(12)
3 实验结果与分析
3.1 实验数据
数据来源于复旦大学计算机信息与技术系国际数据库中心自然语言处理小组整理的训练和测试语料库.在20个类别当中,选取了政治、体育、计算机、艺术、经济、环境和历史这7个文档数目较多的类别作为实验训练、测试集.语料集为各类文档分布不均匀的语料集,各类文档具体的选取情况如下表所示.

表1 语料集上训练集和测试集的选取情况
3.2 评价指标
本文采用文本分类中最常用的性能评价指标查全率(recall)、查准率(precision)和F1.
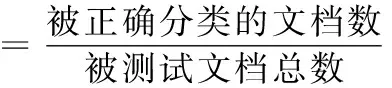
(13)

(14)
(15)
式(15)中:r表示查全率;p表示查准率;
3.3 实验过程
3.4 结果分析

表2 不平衡数据集下的对比实验结果

4 结 语