多对极发电机励磁绕组匝间短路故障在线定位理论研究

李帅轩，刘玉明，陈 俊，王洪林，李杨松，王坤杰，郝亮亮

（1．湖北白莲河抽水蓄能有限公司，湖北省武汉市 430000；2．南京南瑞继保电气有限公司，江苏省南京市 211102；3．北京交通大学电气工程学院，北京市海淀区 100044）

0 引言

发电机的励磁绕组在高速运行或频繁启动中容易发生因线圈之间相互挤压和摩擦造成的励磁绕组匝间短路故障[1]。虽然轻微的短路故障不会对发电机运行造成明显影响，但如果不能及时排除故障，可能会导致发电机励磁电流显著增加，输出无功功率减小，机组振动加剧，烧伤轴颈和轴瓦，严重威胁发电机和电力系统的安全、稳定运行。

近年来，国内外学者对发电机励磁绕组匝间短路故障的在线监测进行了一系列的研究[2-5]，采用定子分支谐波环流总有效值对励磁绕组匝间短路故障进行监测[6]已被论证是一种有效的解决方案。目前相应的在线监测装置已应用于浙江新安江、宜兴抽水蓄能和二滩等多座水电站。二滩水电站的在线监测装置在2018年成功实现了对故障报警，但同时发现停机后定位动态短路故障的难度很大。如果能够在发电机运行中对故障进行定位并及时排除，能有效减少故障排查时间。

目前实际应用较多、较成熟的转子匝间短路故障定位技术是离线故障定位，然而动态匝间短路故障是与转子运动紧密相关的（如线圈之间相互挤压造成的短路），即使在线监测已经发现了故障，但在停机后可能无法找到故障的位置。因此，离线故障定位仅仅适用于静态匝间短路故障。对于多对极发电机励磁绕组匝间短路故障的在线定位技术而言，故障磁极的定位是关键，只有先找到故障磁极的位置，才能实现故障线圈的定位。

目前学术界对故障在线监测与定位的研究进展相对有限，文献[7]分析了转子匝间短路故障位置和故障程度对定子谐波电流的影响，但未明确故障监测及定位方案；文献[8]研究发现在空载工况下，定子奇数次谐波电势变化量的比值、并联支路偶数次谐波电流的比值与励磁绕组匝间短路故障的位置存在对应的关系，据此可判断出故障线圈的位置；文献[9]基于理论分析与实验结果，对分布式励磁绕组的故障位置和短路匝数对故障特征量的影响进行了研究，并利用定子分支谐波电流的故障特征对故障线圈进行定位。由此可见，当前研究大多集中在隐极发电机故障线圈定位的相关研究上（往往都是1对极），而对于故障磁极定位的研究还远不够充分和深入，需要进一步深入研究。

本文对多对极发电机励磁绕组匝间短路故障的在线定位展开研究，基于一台3对极、12kW的多对极发电机动模样机研究在线定位的理论基础。理论基础整体分为两个部分：一是准确计算故障的数学模型，二是在线定位方法的理论依据。为此，本文在准确计算多对极发电机转子匝间短路故障的基础上，基于仿真和实验，对定子分支谐波环流的时域特征进行分析；找出分支谐波环流特征波峰和波谷与故障磁极位置的关系。

1 励磁绕组匝间短路故障的场路结合数学模型

1.1 基于场路结合法的故障计算模型

多回路分析法能够深入发电机的定子和转子绕组内部，计及气隙中各种空间谐波磁场，计算出定子所有支路以及励磁绕组和阻尼回路的电流、电压。采用该方法分析励磁绕组匝间短路故障的基本思路是：将发电机的定、转子视作相互运动的电路，分析各实际回路的电压与磁链关系。

在充分考虑故障引起的励磁绕组电路拓扑结构改变和定子相绕组内部出现的分支谐波环流[10]，基于多回路分析法可列出以定子和转子所有实际回路电流为待求量的标准状态方程：

式中：I′表示定子电枢、转子励磁绕组（包括正常和故障回路）以及转子阻尼绕组各回路的电流；E表示电网电压和励磁电源电压，为已知量；M′和R′分别表示由各实际回路的电感矩阵和电阻矩阵，其中，电感矩阵M′中会随着同步发电机转子的运动而发生变化，是时变矩阵；而MT和RT为常数矩阵，其数值包括电网线路参数、变压器的电阻和漏电感、励磁绕组的内电阻、内电感等相关参数。

式（1）为转子励磁绕组发生匝间短路故障时，同步发电机的多回路数学模型，该模型的本质是变系数的常微分方程。求解该模型之前需要首先求得电感矩阵，多回路分析法以绕组的单个线圈为分析对象，计算得到每个线圈的电感参数，然后根据故障时定、转子绕组的实际连接情况，由有关线圈的参数计算得到各绕组回路参数，具体方法参见文献[10]。

相比于简单的在线监测，在对多对极发电机励磁绕组匝间短路故障的研究中需要数学模型的计算更加准确。但多回路分析法在计算参数的过程中会对发电机实际的气隙磁场做一种近似考虑，存在一定的偏差。而场路耦合法的计算速度又太慢，不能满足实际工程的需求。本文采用场路结合法计算多对极发电机的励磁绕组匝间短路故障，采用有限元法计算标准状态方程中的各实际参数，能够兼顾计算精度与计算时长。

如图1所示为场路结合法计算电感参数的流程图。首先，根据发电机的实际运行状态加载励磁电流，负载时根据实际转子位置由负载运行时的相量图计算相电流，然后进行磁场求解和电感计算。此时可以考虑发电机故障前的实际运行状态，而在短路匝数较少的情况下，故障不会引起磁场太大的变化，该参数将非常接近于实际情况。通过有限元计算的实际工况电感参数带入式（1），可计算得到故障时各回路电流。

图1 电感参数的计算流程Figure 1 Calculation flow of inductance parameters

1.2 数学模型的实验验证

为验证多对极发电机的励磁绕组匝间短路故障场路结合计算模型的正确性，在一台3对极的同步发电机上进行了故障实验，发电机的主要参数如表1所示。

表1 实验样机的基本参数Table 1 Basic parameters of experimental generator

如图2所示为实验的原理接线图，直流电动机由西门子6RA70调速设备做驱动，进而拖动实验样机保持在额定转速1000r/min。一台高精度直流稳压电源提供给同步发电机样机励磁。由一台三相调压器作为变压器实现发电机样机与系统的并网。

图2 励磁绕组匝间短路实验接线图Figure 2 Experimental wiring diagram of inter turn short circuit in field winding

如图3所示为实验样机在联网时励磁绕组4和5抽头之间发生匝间短路时的稳态实验波形和仿真波形，实验时同步发电机的励磁电压为6.03V，发电机机端线电压有效值为188.4V。

由图3的对比可见，仿真波形和实验波形两者吻合得很好。为了进一步验证场路结合计算模型的准确性，通过傅里叶分解得到故障后实验和计算结果各次谐波的有效值，如表2所示。对比文献[10]中采用多回路分析法的计算结果，场路结合模型的计算误差更小，充分验证了模型的准确性。

表2 仿真与实验稳态波形的各次谐波对比Table2 Comparison of harmonics between simulation and experiment

图3 实验波形与仿真波形的对比Figure 3 Comparison between experimental and simulation

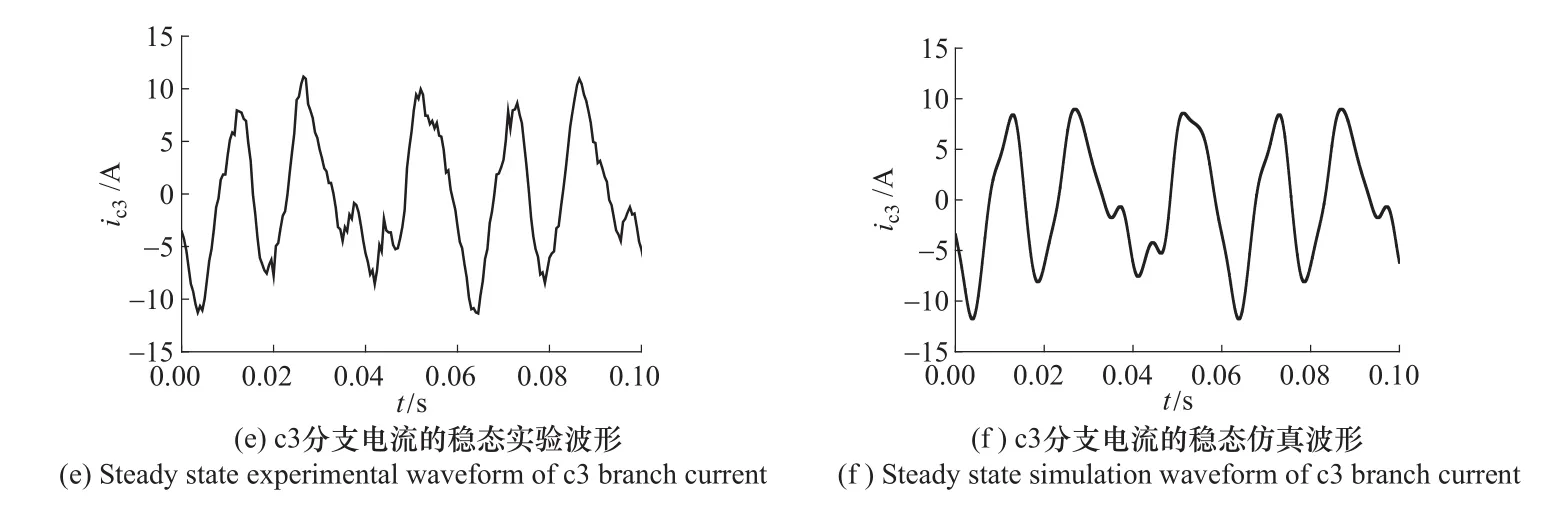
图3 实验波形与仿真波形的对比（续）Figure 3 Comparison between experimental and simulation

2 多对极发电机励磁绕组匝间短路故障分支谐波环流的时域特征分析

2.1 总体思路

如图4所示为发生励磁绕组匝间短路时的励磁回路示意图，可将故障后发电机的励磁绕组分成正常励磁回路和励磁故障附加回路。图中，正常励磁回路的电流为if；励磁故障附加回路的电流为ifkL；EZF为励磁电动势；RfkL为励磁短接线的电阻。

图4 故障励磁回路示意图Figure 4 Diagrammatic sketch of fault field windings

若不考虑发电机磁路的饱和，转子某一极下的匝间短路故障可看作正常励磁绕组产生的磁场与故障励磁绕组产生的故障磁场的叠加。而正常磁场不会感应出分支谐波环流，故障磁场将随着发电机转子的运动改变定子分支谐波环流。而目前大型发电机一般都安装有转轴鉴相传感器，利用其发出的鉴相信号配合发电机的转速信号可准确获取任意时刻的转子位置角，从而为定子不平衡电流打上时标（得到不平衡电流随转子位置角变化的波形）。

如图5所示，以一台2对极的发电机为例进行简要说明，该发电机的定子绕组每相由相同极性下的两分支正向并联而成，在由鉴相脉冲和转速信号获取到转子位置信息后便可给相电流和不平衡电流打上时标。经理论分析易知，若位于转子d轴的1号磁极发生短路故障，则不平衡电流的特征波峰和波谷分别出现在1号磁极和3号磁极中心正对A1分支中心的时刻。对不平衡电流中的1/2次谐波的波峰和波谷的分析类似，不再详述。

图5 故障在线定位方法的示意图Figure 5 Diagrammatic sketch of on-line location method of inter-turn short circuit fault

由上述简单分析可知，励磁绕组匝间短路故障后分支谐波环流的时域特征分析是进行故障磁极在线定位的关键，下面以实验样机为例展开具体论述。

2.2 基于实验样机的时域特征分析

2.2.1 初始位置的确定

如图6（a）所示为实验样机定子分布示意图，可以看出，定子每个分支由不同极下的两个线圈组反向串联而成。以实验样机A相第1分支和第2分支回路中的环流为对象，可以确定出该回路绕组的轴线位置如图6（b）所示。当t=0时，转子1号磁极d轴的位置为定子坐标系的原点。

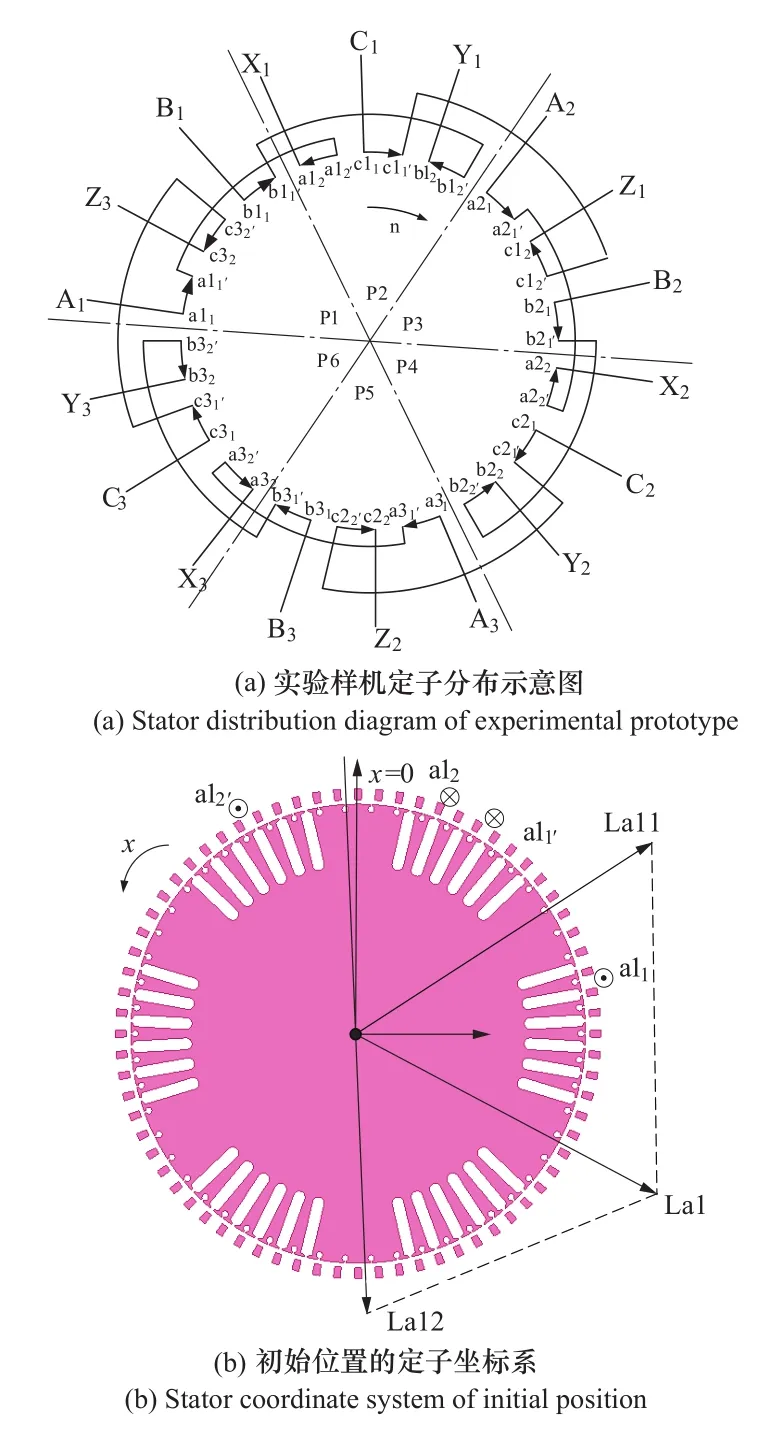
图6 实验样机的定子坐标系Figure 6 Stator coordinate system of experimental generator

2.2.2 故障后励磁磁动势与故障位置的关系

励磁绕组发生匝间短路故障后将首先改变励磁磁动势，而从定子坐标系看，故障磁动势的相位与故障磁极的位置关系密切。如图7（a）所示为实验样机第1极短路时的磁动势实际波形，对该磁动势进行傅里叶分解可以得到各次空间谐波磁动势。如图7（b）所示为其中的1/3次和2/3次磁动势的波形图，为了方便不同次数磁动势之间的相位比较，将各次谐波磁动势的大小均设为1。从图中可以看出，各次谐波磁动势的波峰均与发生短路故障的转子1号磁极d轴的位置相重合（即定子坐标系的原点）。

图7 故障励磁磁动势Figure 7 Excitation magnetomotive force of fault

2.2.3 定子电动势与故障励磁磁动势的关系

故障励磁绕组产生的磁动势会随转子同步旋转，进而在定子分支感应出不平衡谐波电动势。如图8所示为定子回路谐波不平衡电动势产生的示意图，因此由A相第1分支和第2分支组成的回路中的不平衡谐波电动势为：

图8 定子回路谐波不平衡电动势的示意图Figure 8 Diagrammatic sketch of harmonic unbalanced electromotive force in stator circuit

其中，ea1和ea2分别为第1分支和第2分支的谐波电动势；ψS1和ψS2分别为第1分支和第2分支的磁链。

值得一提的是，由式（2）可知回路不平衡谐波电势的相位滞后于回路不平衡磁链90°，但因为磁链不仅仅包含励磁磁链，还包含故障时的阻尼回路和其他定子回路的互感磁链，导致定子回路谐波不平衡电动势的波形相位与励磁磁动势之间的相位并非是90°。图9为计算得到的定子回路1/3次和2/3次谐波不平衡电动势波形随转子位置变化的波形。可以看出，转子位置角为零时两波形确实基本处于波谷，但存在一定的偏差。

图9 定子回路谐波不平衡电动势波形Figure 9 Waveform of harmonic unbalanced electromotive force in stator circuit

准确的计算表明，1/3次谐波不平衡电动势的波谷处于6.9°的位置，而2/3次谐波不平衡电动势的波谷有两个，分别处于 23.5°和 204.4°。

2.2.4 分支谐波环流的相位

定子回路谐波不平衡电动势将在回路中产生分支谐波环流，分支谐波环流的相位取决于回路的电阻和电感，与发电机所带的负载没有任何关系。回路的阻抗角φZ,μ为：

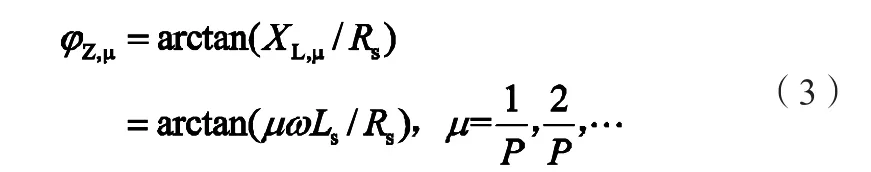
式中：XL,μ为回路中μ次不平衡电流所遇到的电抗；Rs为回路电阻；ω为同步角频率；P为电机的极对数。

实验样机的回路电阻为0.22Ω，漏电感为0.674mH，由式（3）可以计算得到1/3次谐波不平衡电动势与分支谐波环流之间的相位差为17.1°，2/3次谐波不平衡电动势与分支谐波环流之间的相位差为15.795°。

如图10所示为计算的1/3次和2/3次分支谐波环流波形，1/3次分支环流的波谷位置为24°，2/3次分支环流的两个波谷位置分别为40.2°和220.2°。对比可知，计算的1/3次和2/3次谐波不平衡电动势与分支环流之间的相位差分别为17.1°和15.8°，与理论分析吻合。

图10 分支谐波环流波形Figure 10 Branch harmonic circulation waveform

2.3 总结与讨论

本章前两节沿着故障励磁绕组产生的磁动势、故障磁动势产生的定子回路谐波不平衡电动势、电动势谐波激发的分支谐波环流这一主线详细分析了多对极发电机励磁绕组匝间短路故障分支谐波环流的时域特征。通过分析可以清楚地看到，在确定了初始位置，对磁极进行编号后，故障磁极的位置将直接与分支谐波环流的相位建立起联系。其中谐波环流的1/P次谐波能唯一锁定故障磁极位置，而利用单一的其他次谐波会出现多解的情况。

在具体实际应用时，首先设置好转子的磁极编号，并确定定子的参考点；当转子旋转到该参考点时，计算定子分支环流的1/P次谐波相位角，通过将相位角与根据计算值预设的相位角相比较，即可确定故障磁极。

3 结论

本文从故障的场路结合数学模型及分支谐波环流的时域特征两方面构建了多对极发电机励磁绕组匝间短路故障在线定位的理论基础，并通过动模实验验证了模型及相关分析的正确性。研究表明，定子分支环流的1/P次谐波相位角可以用于对故障磁极的判断，本文为实现故障的在线定位提供了依据。