不同空泡动力学模型在空泡振荡预测中的应用探讨
2021-05-14杜煜心芦洪钟姚志峰耿思远王福军
杜煜心,芦洪钟,姚志峰,3,耿思远,王福军,3
[1.中国农业大学水利与土木工程学院,北京市 100083;2.上海凯泉泵业(集团)有限公司,上海市 201804;3.北京市供水管网系统安全与节能工程技术研究中心,北京市 100083]
0 引言
空蚀会造成水力机械运转性能下降,降低工作寿命及安全性能,造成巨大经济损失[1],严重影响水电站或水泵站经济稳定运行。目前普遍认为空蚀主要是由“空泡溃灭—回弹—再溃灭”振荡过程中产生的高压冲击材料表面导致[2]。
为了理论解析空泡振荡行为,最早由Rayleigh[3]提出了理论模型,建立了理想不可压缩流体中球形空泡的运动模型。之后,Plesset[4]在此基础上进行了一系列完善,引入泡内气体、考虑表面张力和液体黏性,建立了Rayleigh-Plesset(R-P)模型。为了进一步考虑液体可压缩性的影响,Herring、Gilmore和Keller[5]等学者进一步修正了R-P模型,提出了Gilmore和Keller-Miksis(K-M)模型。各种空泡动力学模型考虑因素有所侧重,都被广泛地应用于现在的空泡动力学研究。然而,空泡动力学研究中仍有许多问题值得探讨,目前还难以给出一个综合考虑各种因素的普适性模型。
本文针对不同空泡动力学模型在空泡振荡过程中的应用展开探讨,将三种主流空泡动力学模型计算结果与实验空泡的半径值对比,从空泡生长和回弹两个角度,对比各个模型的预测精度,分析各个模型的应用特点,综合分析不同模型在预测空泡运动不同阶段的适用性。
1 空泡动力学理论模型
1.1 Rayleigh模型
Rayleigh模型为单空泡动力学的基础模型,该模型假定球形空泡内部不存在任何物质,且置于均匀无限流体中,忽略液体压缩性和黏性,空泡径向运动方程可表示为:

式中:ρ——液相密度;
R——空泡半径;
pi——气泡界面处的压强,本文取2330Pa;
pe——环境压强,本文取1×105Pa。
需要指出的是,Rayleigh模型在计算空泡溃灭时在溃灭点将得到无穷大的速度,且不发生回弹,这显然背离实际情况。
1.2 Rayleigh-Plesset(R-P)模型
Plesset[4]对Rayleigh模型进行了一系列完善,建立R-P模型,如下:

其中:
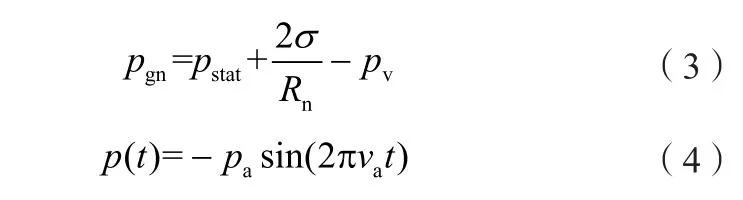
式中:t——时间;
σ——表面张力系数;
μ——液相动力黏度系数;
pgn——静止时气泡内的压力;
pstat——静压;
pv——恒定气压;
κ——惰性气体多变指数;
Rn——平衡半径;
pa——驱动压力振幅;
va——驱动频率。
相比Rayleigh模型,R-P模型的假定条件更为复杂,不仅考虑了空泡表面张力和液体黏性,使水体情况更接近实际,而且考虑了泡内的永久气体,因此,R-P模型解决了空泡回弹问题,即空泡溃灭到最小半径后再次生长,在忽略流体可压缩性和气泡表面的变形运动时,它能够较好地预测空泡的运动。然而,R-P模型的推导过程中依然采用了较多简化和假设约束,如空泡始终保持为球形、空泡内均匀、流体不可压缩和不计热传导等。
1.3 Gilmore模型
Gilmore模型考虑了声音辐射,将空泡的表面看作一个球形扬声器的膜,声音辐射从振荡的气泡中吸收到液体中[6],同时也考虑了空泡表面张力、液体黏性、腔内气体和液相压缩性,其中声速和液相密度均是变量,适用于振幅较大的空泡振荡[7],其模型式为:
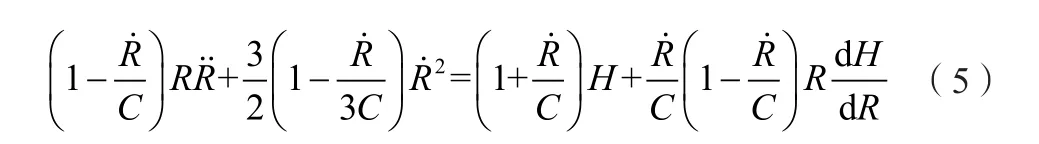
式中:H——焓;
C——与时间相关的声速,其表达式如下:
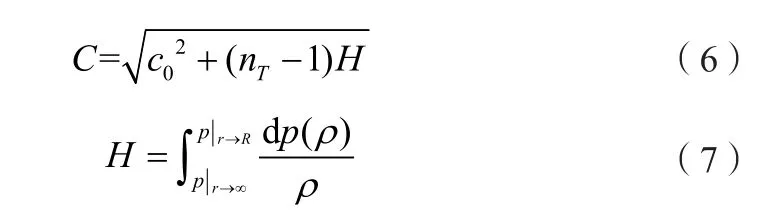
1.4 Keller-Miksis模型(K-M模型)
K-M模型[6]也考虑了振荡气泡的声辐射,但是同时添加了辐射延迟时间的因素,即存在t-R/c的延迟时间,K-M模型同样是在假定声速恒定的情况下考虑液体的可压缩性,其方程式为:
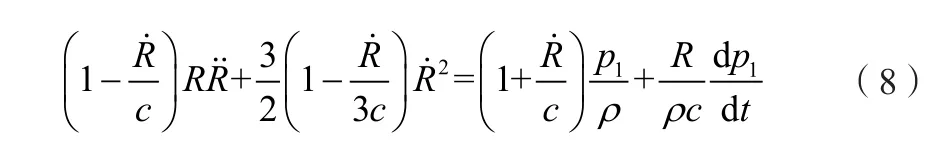
其中:

以上是空泡动力学发展过程中较为典型的四种模型。Rayleigh对早期空泡模型进行了改进,提出了空泡动力学的基础模型。Plesset等在空泡问题中分别发展了这个运动方程,使空泡动力学的理论研究达到了一个里程碑,在此基础上发展出多种类型的空泡动力学模型,如考虑压缩性的Gilmore模型和K-M模型等。选取其中的R-P模型、Gilmore模型和K-M模型开展后续研究,三种模型的基本信息见表1。

表1 三种空泡动力学模型信息汇总表Table 1 Information summary of three kinds of cavitation dynamics equations
2 计算结果与对比
2.1 空泡生长过程
空泡生长过程选用耿思远[7]等人的实验数据,实验为激光诱导空泡,采用双腔激光照明拍摄空泡生长过程的双曝光图片,可达到纳秒量级的时间分辨率。本文理论公式计算采用与实验值相同的初始时间、半径和速度,生长过程初始半径为0.1352mm,初始速度为165.6m/s,计算时间范围为0.209~170μs。实验结果与三种空泡动力学模型计算结果对比分析,半径值如图1(a)所示,速度值如图1(b)所示。各模型在空泡生长过程计算中使用参数见表2。由图1(a)可以看出,R-P模型在空泡发展初期吻合度较差,后期吻合度较好;Gilmore模型和K-M模型与实验值整体吻合度很高。由图1(b)可以看出,三种模型的速度值与实验值均有较好的吻合。由此可见,在空泡的生长过程中,相对其他两种模型,假定条件相对简单的R-P模型与实验值的拟合度更差,而考虑压缩性的Gilmore模型和K-M模型能与实验值有较好的吻合度。

图1 生长过程空泡壁实验值与理论模型对比图Figure 1 Comparison of experimental results and theoretical model of cavity wall in growth process

表2 三种模型生长过程计算参数表Table 2 Table of growth process parameters for three models
2.2 空泡回弹过程
回弹过程三种模型计算空泡半径与两组不同实验值对比结果如图2所示。图2(a)实验数据来源于Kroninger[8]等人,实验值为粒子追踪测速方法(PTV)所得;图2(b)实验数据来源于Ohl[9]等人,实验值为高速摄像所得。图2(a)初始半径为0.747mm,初始速度为0m/s,计算时间范围为70.6~176μs,图2(b)初始半径为0.1794mm,初始速度为-96.2m/s,计算时间范围为0~2μs,各模型在空泡回弹过程计算中使用参数见表3。由图2(a)可以看出,三种模型在空泡收缩阶段与实验值基本一致,但在随后的回弹过程R-P模型与实验值相差甚远;Gilmore模型和K-M模型与实验值整体吻合度很高。由图2(b)可以看出,三种模型在0.3μs内与实验值基本一致,但随后R-P模型值与实验值相差甚远;Gilmore模型和K-M模型与实验值整体吻合度很高;相对K-M模型,Gilmore模型计算所得溃灭空泡最小半径更小。由此可见,在空泡的收缩回弹过程中,考虑压缩性的Gilmore模型和K-M模型更贴近较小空泡的回弹过程,对于较小空泡的回弹,Gilmore模型对溃灭点的计算更为准确。
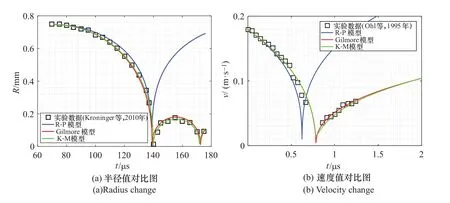
图2 回弹过程空泡壁实验值与理论模型对比图Figure 2 Comparison of experimental values and theoretical model of cavity wall in rebound process

表3 三种模型溃灭过程计算参数表Table 3 Table of collapse process parameters for three models
2.3 讨论
探讨了三种不同空泡动力学模型在空泡振荡过程中的应用,从空泡生长和收缩回弹两个角度出发,分析各模型的运用。在Rayleigh模型的基础上,R-P模型突破性地解决了空泡回弹问题,但其未考虑压缩性和声辐射,因此与实验有偏差。K-M模型在假定声速恒定的情况下考虑了泡壁处的压缩性,Gilmore模型将声速和液相密度作为变量,两种模型均可以相对准确地描述各种空泡运动,同时Gilmore模型对微米尺度回弹空泡溃灭点的预测更为准确。
3 结论
本文针对空泡生长和回弹过程的理论预测问题,以空泡半径值为对比参数,分析了三种空泡动力学模型和实验值之间的差异,发现Gilmore模型和K-M模型预测结果与两个空泡振荡参照实验结果均吻合较好。分析后认为,这两种模型可以更准确地描述毫米尺度空泡生长和空泡的回弹溃灭过程,其中,Gilmore模型对微米尺度回弹空泡溃灭点的预测更为准确。
