不同工况下水泵水轮机尾水管压力脉动特性与改善措施研究
2021-05-14武文强李丽婷吕蕊蕊
武文强,李丽婷,吕蕊蕊,于 安
(河海大学能源与电气学院,江苏省南京市 210003)
0 引言
随着科技不断发展,用户对电量的需求日益增加,水泵水轮机朝着高水头、高容量与高速化方向发展,高水头下运行的机组空化性能变差,压力脉动幅值明显增大,会使机组在部分工况下由压力脉动产生剧烈的水力振动,若振动频率与电站厂房固有频率相同则会引起共振,严重威胁电站与机组的正常运行,因此,研究水轮机在非设计工况下由压力脉动产生的水力振动这一现象具有重要意义。
早期针对尾水管压力脉动与涡流关系的研究主要集中在试验,Sirok等[1]通过试验发现涡带的结构脉动与其压力脉动的相似性。Miyagawa等[2]通过试验分析了机组在不同工况下涡带的形态。Marko Hocevar等[3]通过径向基神经网络(RBNN)的方法得到了尾水管内部涡带的形态,由于借用了尾水管内部压力脉动的试验数据,该数值计算能较为准确地模拟尾水管内部流动形态。
国内针对尾水管涡带与压力脉动关系的研究主要集中在数值计算与试验相结合分析。杨建明、曹树良等[4]基于k-ε两方程湍流模型完成了对尾水管三维湍流模拟的编程,得到了尾水管内部流态特征;张双全等[5]对原型尾水管进行了三维非定常数值模拟计算,得到了尾水管内涡带形态的变化规律,将数值计算结果与实验数据进行了比较分析;周凌九等[6]发现尾水管涡带受转轮出口圆周速度与回流区大小这两个因素影响,机组的压力脉动随着空化系数装置减小而逐渐增大,当空化系数装置数值减小到某一数值压力脉动也达到一最大数值[7-8];季斌等[9]针对水轮机小流量工况进行三维非定常数值计算,分析了尾水管内涡带形态和低频压力脉动的变化规律;郭涛等[10]通过滑移网格和基于Vreman亚格子模型的全局动态大涡模拟方法得到了尾水管内特殊的流场动态信息;齐继贺[11]应用CFD数值模拟,观察到尾水管随导叶不同开度变化时,尾水管涡带由双螺旋涡带到单螺旋涡带至柱状涡带的变化过程;李广府[12]根据模型试验结果,如实记录了随着导叶开度变化和空化系数降低的尾水管涡带演变过程;徐用良等[13]通过试验方法研究了模型试验水头和空化系数对混流式水轮机对尾水管压力脉动的影响。
国内外学者针对尾水管涡带的研究主要集中在出现螺旋涡带的工况,而对于水泵水轮机来说运行工况区间宽广,对于小流量、设计流量、大流量这三种区间工况的总结性研究较少。对于尾水管涡带的处理国内外学者也对其进行了大量的研究,提出了相应的改善措施。尾水管涡带产生需要具备两个基本条件:一是需要一定数值的圆周速度和轴向速度;二是要有一定的发展空间,因此,改善涡带或者减小涡带压力脉动的方法,需要从这两个条件入手[14]。若能了解尾水管涡带的产生原因,就可以提出相应的手段控制涡带的发展,以减小机组受水力振动引起的破坏,保证水泵水轮机的安全运行。因此,本文通过数值模拟分析不同流量、不同空化系数下尾水管涡带演变形态规律和低频压力脉动特性,并在此基础上提出了相应的改善措施,对进一步研究水泵水轮机稳定运行具有重要意义。
1 数值计算模型
1.1 控制方程
连续性方程、动量方程和能量守恒方程为描述流动的三大基本方程,在水力机械计算中,一般不考虑温度的变化,认为机组内部流场为等温且不可压缩的三维流动场,所以求解过程可以忽略能量方程。连续性方程又称质量守恒方程,其表达如下:

其张量形式为:

动量方程在流体力学中的表述为Navier-Stockes方程,其表达如下:

式中:ρ、p——流体密度和压力;
ui、uj——不同方向的流体瞬时速度值;
μ——动力黏性系数;
μt——湍流黏性系数。
1.2 湍流模型
标准k-ε湍流模型的控制方程为:

式中:k——湍动能;
ε——湍流耗散率;
Pt——湍动能生成项。
模型 常数分别为 :Cε1=1.44,Cε2=1.92,σε=1.3,σk=1.0。湍流黏性系数μt定义为:
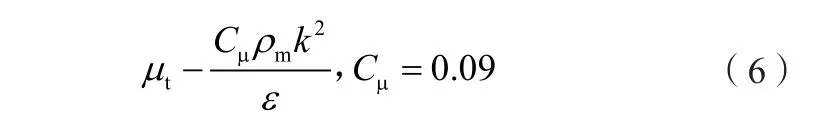
本文选取了基于k-ε模型的滤波修正模型,即FBM湍流模型,该模型k方程和ε方程形式不变,湍流黏性系数μt为如下定义:

式中:F——滤波函数,由滤波尺寸λ和湍流长度比的比值大小决定,定义为:
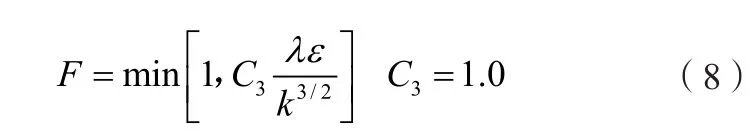
对尺度小于滤波尺寸的湍流,采用标准k-ε模型,当湍流尺度较大时,黏性系数表达式为:
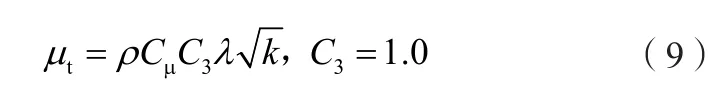
1.3 空化模型
对于水轮机水泵空化数值计算,本文采用了均相流空化模型。空化的过程包括水蒸气和水,其中描述气相的连续方程为:
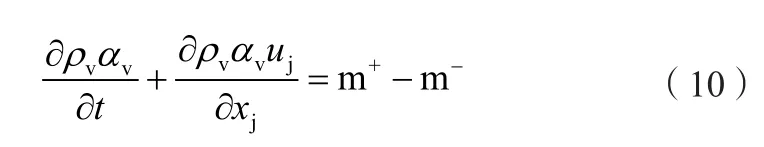
式中:m+、m-——表示水蒸气蒸发和凝结过程的源项;
ρv——汽相密度值;
αv——蒸汽体积分数。
该空化模型假定单位体积内所有空泡大小相同,ZWART认为在空化现象发生中核子的体积分数是变化的,随着水蒸气体积分数增加,核子的密度必然减少[15-16]。
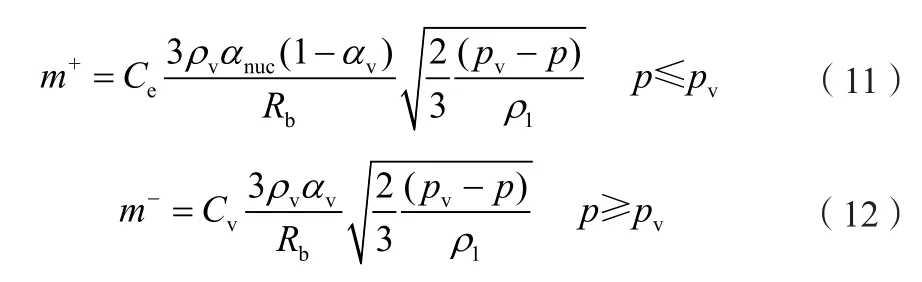
式中:Rb——气泡半径,为1×10-6m。αnuc=5e-4,Cv=0.01,Ce=50。
1.4 水泵水轮机模型及网格划分
本文研究所使用的水泵水轮机模型如图1所示,其主要参数如表1所示。
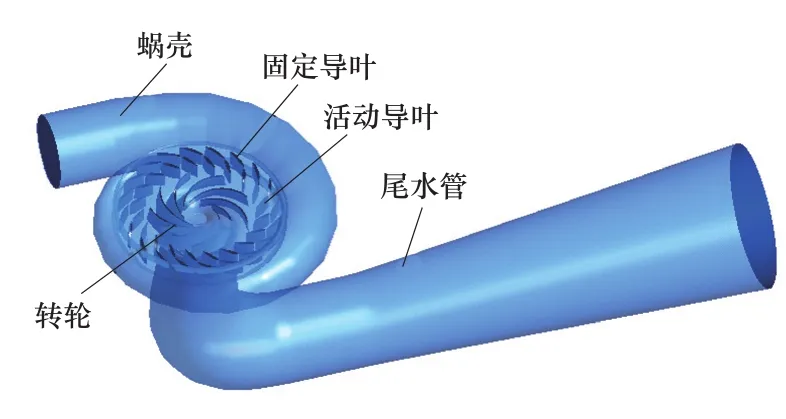
图1 水泵水轮机几何模型Figure 1 Geometric model of pump turbine

表1 水泵水轮机模型主要参数Table 1 Main parameters of pump turbine
基于水头、效率这两个参数进行网格无关性验证如表2所示,最终选取方案3,网格总数量为330万,尾水管网格如图2所示。

表2 网格无关性验证Table 2 Grid independence verification

图2 尾水管模型结构化网格Figure 2 A structured grid for draft tube
流体介质选用Water at 25℃、Water Vapour at 25℃,水轮机工况下进口处采用流量条件,出口处采用压力条件,转轮进出口的交界面设为 Frozen Rotor,收敛残差为10-4。计算结果稳定后取时间步长为0.000333333s(转轮旋转3°),总的计算时间为100Tn,选取最后10个周期的数据进行分析。
2 计算结果与分析
2.1 监测点设置及空化系数的确定
为分析不同流量下水泵水轮机尾水管的压力脉动特性,在尾水管处设置了相应的监测点,如图3所示。尾水管监测点wi2、wm2与wi3、wm3所在的水平界面距离尾水管进口距离分别为0.2m、0.4m,监测点wi4、wm4、wo4位于尾水管弯肘段,监测点wi5、wm5、wo5位于尾水管扩散段。

图3 水泵水轮机尾水管监测点设置Figure 3 Monitoring points at draft tube
空化系数σ的计算公式为:

式中:Pout——尾水管出口压力,Pa;
Pv——25℃饱和蒸汽压力,Pa;
Hs——水轮机吸出高度,m;
H——水头,m;
ρ——密度,kg/m3;
g——重力加速度,一般取9.8m/s2。
针对同一流量工况下分别选择无空化与发生空化的两个工况点。在110%Qr下,当空化系数低于0.177时,转轮叶片和尾水管内部充满空泡,出口流量几乎为0,空化极其严重,因此选择该流量下的空化系数0.299。表3为非定常数值计算的工况。

表3 非定常数值计算工况的确定Table 3 Determination of unsteady numerical conditions
为了验证数值模拟的有效性,针对不同流量的工况进行数值计算,并与试验数值比较,结果见表4。由表格可知各工况下误差保持在3%之内,证明了数值模拟计算的准确性,同时也说明了FBM模型选取是合理的。

表4 不同流量下数值模拟计算误差Table 4 Numerical simulation error at different flow rates
2.2 不同工况下的涡带演化研究
随着流量的不同,尾水管涡带呈现出不同的形状和尺寸,选取不同流量工况下涡带图进行分析,由图4可知,在σ=0.401下,50%Qr工况时为偏心距较大的双螺旋涡带,涡核直径较大,其中一条螺旋涡带较为纤细且长度较短,涡带形态极不稳定,涡带周向运动到弯肘段位置后逐渐消失;70%Qr工况时为螺旋强度较大的单螺旋涡带,偏心距减少且形态比较稳定,涡带结构较长且比较纤细,涡带在弯肘段入口处逐渐消失,涡核直径变小;90%Qr工况时的涡带为细长柱状且未出现偏心,只有尾部有轻微的螺旋状,涡核直径与涡核区域压力减小;100%Qr工况时为旋转幅度较小的双螺旋涡带且未出现偏心,涡核区域压力减小,涡带长度变小,周期内表现较为稳定,形态未发生明显的变化,尾部有小尺度的涡团脱落;110%Qr工况下为梨形柱状涡带且没有偏心,涡带长度与涡核区域压力减小,涡核直径增大。
相比于无空化条件,由图4和图5可知,空化条件下,50%Qr工况时涡带形态变得散乱复杂,周期内并未出现稳定形态的涡带,由于尾水管直锥段和弯肘段内部充满大量空泡,使其内部流动变得更为复杂紊乱,加剧了旋涡流动与回流等不稳定现象的发生,双螺旋涡带消失;70%Qr工况时旋涡强度减小,涡带长度变小,由单螺旋涡带演变为双螺旋涡带,产生的另一条螺旋涡带结构长度较小且比较纤细,形态极不稳定;90%Qr工况时有无空化条件对涡带形态没有明显改变,都是细长柱状,周期内涡带形态稳定,空化发生后涡带长度有所增加,一直延伸到了扩散段入口处;100%Qr工况时尾水管内出现的空泡形态极不稳定,尾水管进口壁面处也发生了空化,由于大量团状空泡的出现改变了涡带的形态,没有稳定形态的涡带产生;110%Qr工况时由梨形柱状演变为形态极不稳定的双螺旋涡带,螺旋强度减小,涡带长度减少。
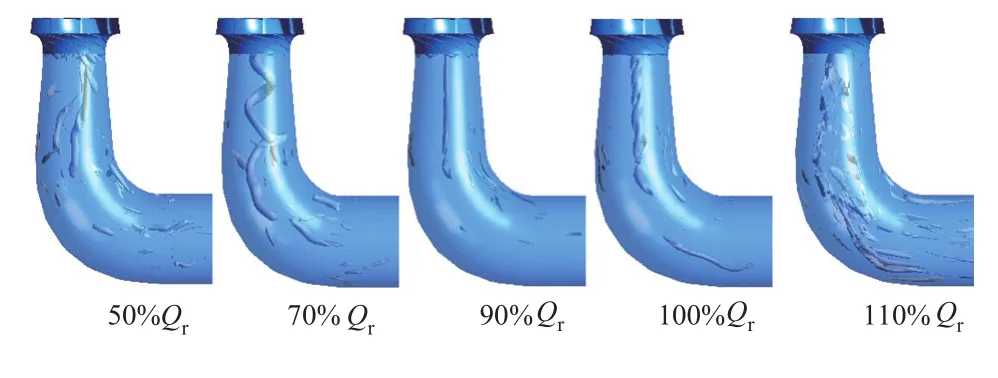
图4 σ=0.401工况下涡带结构示意图Figure 4 A schematic diagram of vortex structure under σ=0.401 condition

图5 空化工况下涡带结构示意图Figure 5 Schematic illustration of vortex structure under cavitation
由以上分析可知,尾水管涡带在不同的工况下形态差异较大,其形态受流量和空化系数影响较大,有单螺旋、双螺旋、细长柱状以及梨形等形态。小流量工况下整体表现为螺旋涡带,大流量工况下为梨形柱状涡带,在设计流量以下,随着流量增大涡带偏心距减小,涡核直径与压力降低,涡带长度增加,接近设计流量工况的涡带螺旋强度较小。空化发生后,对50%Qr与110%Qr两个流量工况影响最大,涡带形态发生明显改变,整体表现为涡带形态极不稳定。
2.3 不同工况下的压力脉动特性研究
由前面分析可知,空化发生后对50%Qr与110%Qr两个流量工况的涡带形态影响最大,下面将计算得到的50%Qr工况的压力脉动进行傅里叶变换得出对应监测点的频谱分析图,如图6,由转速n=1500r/min可得fn=25Hz、Tn=0.04s,为方便比较监测点压力脉动与机组转频之间的关系,取频率横坐标为f/fn。
由图6(a)可知,50%Qr流量工况且未发生空化时,尾水管壁面直锥段与弯肘段监测点主要受0.3fn及其倍频的影响,其幅值沿着壁面向下游的方向越来越小,说明该低频压力脉动随着水流方向对尾水管内部的影响越来越小。由2.2分析可知,50%Qr工况时为偏心距较大的双螺旋涡带,其中一条螺旋涡带较为纤细且长度较短,涡带形态极不稳定,涡带周向运动到弯肘段位置后逐渐消失之后又变成了单螺旋涡带,因此扩散段监测点wi5、wm5压力脉动的主频不再是涡带旋转频率0.3fn,其主要受0.1fn及其倍频的影响;值得注意的是,尾水管进口wi1监测点的主要频率为0.7fn,次要频率为涡带旋转频率0.3fn,这是由于该工况下尾水管进口处出现一较大旋涡,该水流旋涡对尾水管进口处监测点的脉动影响大于了涡带旋转频率。
空化工况下尾水管壁面监测点的主频发生了变化,如图6(b)所示,主要受1.5fn的影响,其幅值随着水流方向不断减小。由2.2分析可知,相比于σ=0.401,50%Qr流量时发生空化后并未出现稳定形态的涡带,由于尾水管直锥段和弯肘段内部充满大量空泡,使其内部流动变得更为复杂紊乱,加剧了旋涡流动与回流等不稳定现象的发生,所以在尾水管入口处和直锥段存在着丰富的低频脉动信号。

图6 50% Qr下尾水管壁面监测点压力脉动频域图Figure 6 Frequency-domain diagram of pressure pulsation at the monitoring points under 50% Qr
为进一步探讨涡带与空化波动引起的脉动对机组运行稳定性的影响,选取尾水管壁面5个监测点对应的压力脉动幅值进行分析,结果如表5、表6所示。表5中给出了未发生空化时(σ=0.401)的压力脉动幅值,其中50%Qr工况下涡带引起的低频脉动幅值最大,而运行工况越接近设计流量时的低频压力脉动幅值越小,且高幅值脉动信息聚集在直锥段和弯肘段,扩散段压力脉动逐渐衰减,即尾水管涡带是水轮机尾水管中的一种流动现象,但是对机组运行稳定性有影响的是螺旋形涡带,涡核中心偏离了尾水管截面中心的位置,造成尾水管截面上的流场信息失去了对称性,不均匀的压力和速度分布流场呈周期性的旋转,使得尾水管内部出现低频脉动,且螺旋强度越大,偏心距越大,产生的低频压力脉动信息越强烈,且在一定流量区间内涡带旋转频率随着流量的增大而略有减小;在相当宽广的工况范围内,尾水管压力脉动均存在着丰富的低频脉动,110%Qr工况下产生的低频脉动信息十分接近且涡带螺旋强度较小,因此涡带引起的低频脉动并不明显,不能准确捕捉到涡带旋转频率数值。

表5 无空化工况(σ=0.401)下的压力脉动幅值Table 5 Pressure pulsation amplitude of the vortex under σ=0.401
如表6所示,由空化演化引起的低频压力脉动在大流量工况下表现得最为明显,引起的压力脉动幅值远远大于其他工况,低频高幅值的压力脉动主要聚集在直锥段与弯肘段,且在扩散段脉动信息不断衰减;机组运行偏离最优工况时,进入转轮叶片的水流都会有一定的冲角,偏离的工况越远,冲角越大,使得流道内部充斥着旋涡、脱流等不稳定流动现象,此时尾水管内部流动更为复杂紊乱,因此,50%Qr和110%Qr工况下都存在着十分丰富的低频压力脉动信息。
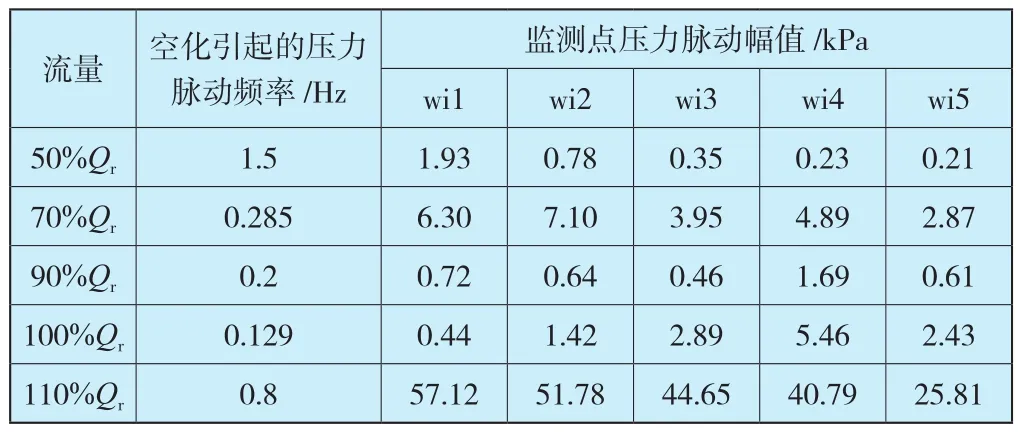
表6 空化工况下的压力脉动幅值Table 6 Amplitude of pressure pulsation caused by cavitation evolution
2.4 改善措施研究
尾水管涡带的形成与转轮出口的圆周速度有紧密联系,在70%Qr工况下转轮出口圆周速度与转轮旋向相同,可在泄水锥上设置与水流旋向相反的4道沟槽,利用抑涡槽削减水流在圆周速度方向上的分量,图7为改善泄水锥结构后的三维模型。

图7 不同泄水锥结构形式Figure 7 Different discharge cone structure
尾水管中导流隔板的宽度a、高度h、厚度b以及安装位置等因素对减小涡带压力脉动的效果都有明显影响,童朝等[17]研究表明,在直锥段加设导流隔板效果最好,结合模型试验得出:隔板上端靠近尾水管进口比较好;隔板垂直高度不宜小于转轮直径的40%,本次模拟的尾水管直锥段加设导流隔板效果图如图8所示,其中,隔板宽度a=75mm,高度h=150mm,厚度b=2mm,隔板上端位置距离尾水管进口截面2mm。

图8 尾水管内导流隔板示意图Figure 8 Draft tube schematic using the baffle
如图9和图10为尾水管流线图和进口截面速度矢量图,无抑涡槽方案下尾水管进口的流线呈螺旋状交互形态,直锥段内流线螺旋强度较大,尾水管进口截面靠近壁面区域的速度方向为顺时针,与转轮旋向相同的速度区域占据了圆形截面的2/3,靠近中心位置出现两个低速区域;有抑涡槽方案下尾水管进口流线方向竖直向下,直锥段内流态良好,除紧贴尾水管壁面的部分流线,螺旋状交互形态消失,进口截面大范围区域的速度旋向发生了改变,速度分布也更加均匀,两个中心低速区域消失,即在有抑涡槽的方案下,明显改善了尾水管内部的流态,特别是直锥段内流体圆周方向上的速度分量被大幅度削减。

图9 尾水管流线图Figure 9 Tail pipe flow diagram

图10 尾水管进口速度矢量图Figure 10 Velocity vector at draft tube inlet
如图11和图12所示为尾水管进口截面与纵向截面压力分布图,无抑涡槽方案下,进口截面存在两个低压区域,由前述可知,该工况下产生了双螺旋涡带,靠近壁面区域有小部分高压区,直锥段内压力分布极不均匀;有抑涡槽方案下,进口截面中心区域低压区消失,靠近壁面的小部分区域出现了低压区,但是截面整体压力数值有小幅度增加,纵向截面弯肘处出现一低压区,弯肘外侧部的高压区位置向下游发生了偏移,此方案下虽然使得靠近尾水管壁面的小部分区域出现了低压区和高压区,但是整体来看尾水管直锥段内部压力分布变得更加均匀。

图11 尾水管进口截面压力分布图Figure 11 Pressure distribution at draft tube inlet
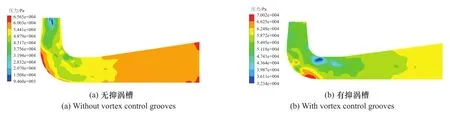
图12 尾水管纵向(Y=0)截面压力分布图Figure 12 Pressure distribution diagram at longitudinal(Y=0)section of draft tube
图13和图14表示采用导流隔板方案的尾水管流线图和截面速度矢量图,其z=-118.49mm时为尾水管进口截面,z=-168.49时截面处于进口与隔板底部之间,z=-288.49mm时截面位于隔板底部以下22mm处,由图14可知,尾水管内部流线顺畅,直锥段与弯肘段均不存在水体螺旋流动,扩散段水流分布变得均匀,相比较抑涡槽方案,导流隔板的存在对下游内部水流流态也有一定积极作用;水流在未通过隔板之前,在尾水管进口截面的速度仍具有较大的圆周速度分量,随着流体不断向下游运动,低速中心逐渐消失,流体与转轮旋向相同的圆周速度分量逐渐地被削减,靠近隔板位置的流体速度较大,速度分布越来越均匀,当流体完全经过隔板,圆周速度分量几乎完全被削减,流体运动方向为竖直向下。

图13 采用导流隔板方案的尾水管流线Figure 13 Flow streamlines in draft tube using the baffle

图14 采用导流隔板方案的尾水管不同截面速度矢量Figure 14 Velocity ve ctor diagram of different sections of draft tube using the baffle
图15为采用导流隔板方案时尾水管内部不同截面压力云图,由图15可知中心位置低压区消失,靠近隔板区域的压力增大,导流隔板方案下改善了直锥段与扩散段径向截面的压力分布情况。即抑涡槽的存在主要对尾水管直锥段的压力、速度分布有改善作用,加设导流隔板之后不仅改善了直锥段内部流态,而且使得水平扩散段的流动变得更加稳定。

图15 导流隔板方案下尾水管内不同截面压力分布Figure 15 Pressure distribution of different sections in draft tube using the baffle
如表7所示,无抑涡槽和导流隔板工况下,尾水管壁面监测点对应涡带脉动最大幅值为6.75kPa,有抑涡槽方案下,直锥段的压力脉动降低比率最大,弯肘段与扩散段的低频脉动幅值降低比率较低,即抑涡槽能够明显改善尾水管直锥段内的低频压力脉动;导流隔板方案下的脉动幅值降低比率数值比较平均,数值没有明显差异,即导流隔板的存在能在整体水平上降低尾水管内部的压力脉动幅值。
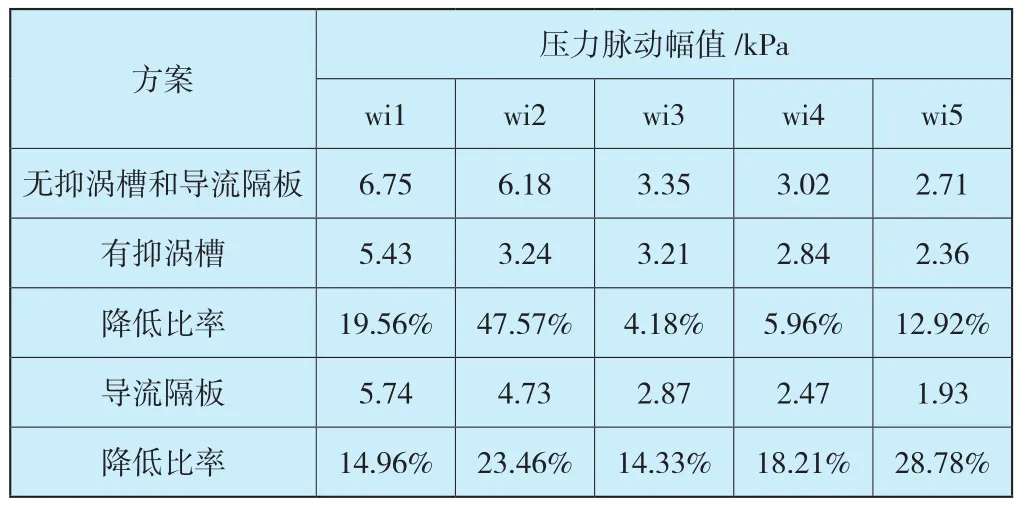
表7 尾水管压力脉动幅值Table 7 Pressure pulsation amplitude in draft tube
在z=-268.49mm高度截取一个圆形截面,过圆心取一条平行于x轴的直线,做这条直线上圆周速度分布曲线如图16所示,两种方案均能有效地减小圆周方向上的速度分量,导流隔板方案下,在-0.075r至0.125r区间上,圆周速度数值均低于0.5m/s,速度数值基本保持在0.5m/s以下,速度梯度变化较小没有突变;抑涡槽方案下,在-0.02r至0.125r区间上,圆周速度数值低于0.5m/s,靠近尾水管壁面区域圆周速度急剧变化,因此,该位置容易出现旋涡运动,由前述可知该方案下靠近壁面处的流线呈螺旋交互形态,而靠近中心区域的速度明显降低,即抑涡槽能够明显削减靠近涡核区域的圆周速度分量,导流隔板能在整体上降低圆周速度分量。
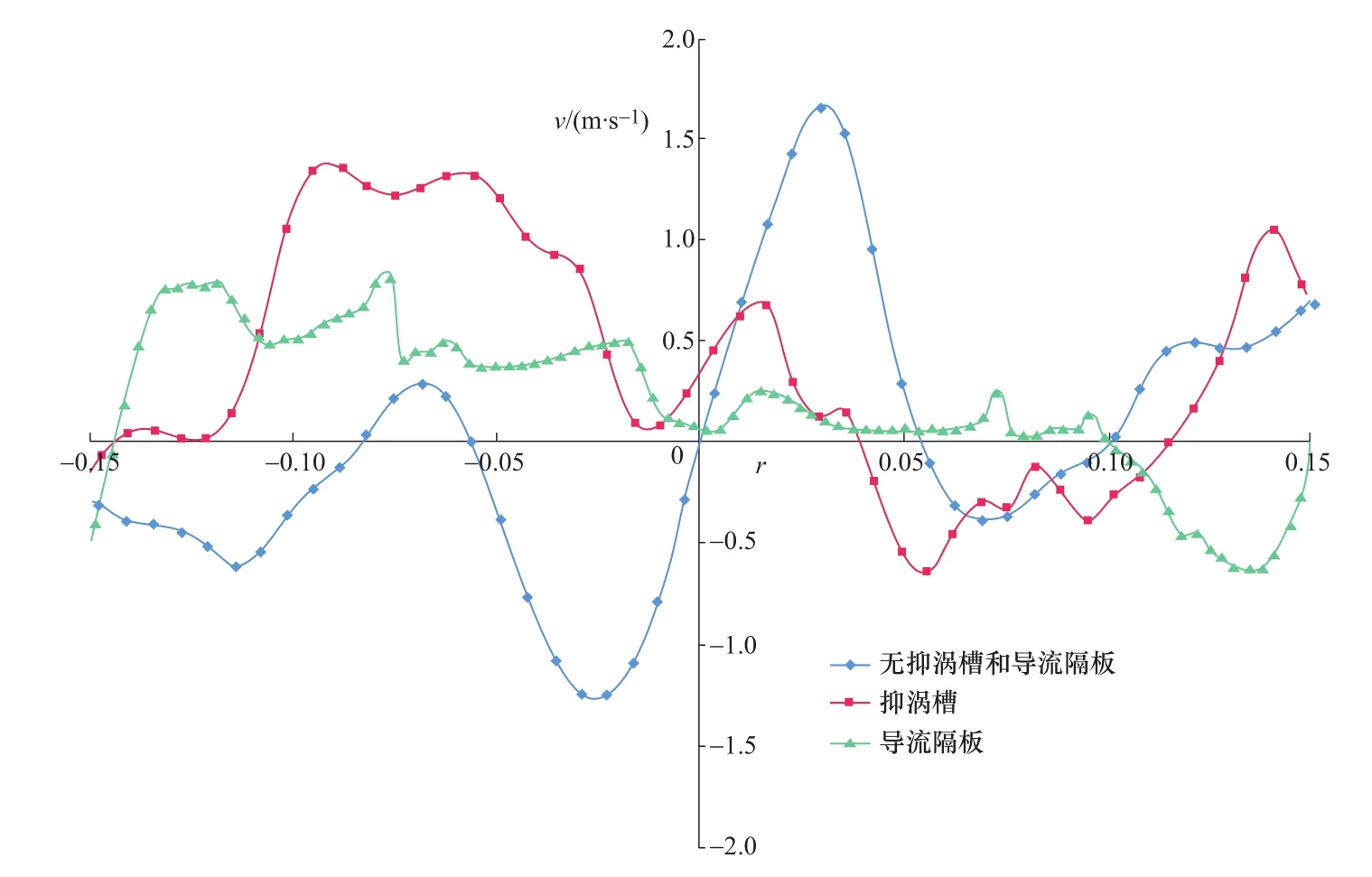
图16 不同方案下圆周速度分布曲线Figure 16 Circumferential velocity curve under different schemes
抑涡槽的存在改变了转轮流域内原有水流的流态,转轮内部结构的变化大大增加了机组的水力损失,由表8可知,机组效率与出力数值大幅度降低;导流隔板方案下,机组效率与出力数值有小幅度的下降。即在70%Qr工况下(σ=0.124),抑涡槽虽能明显降低涡带低频压力脉动,但是水轮机出力与效率数值明显下降,导流隔板方案在水力性能和抑制涡带低频脉动两个方面表现出了较好的优越性。
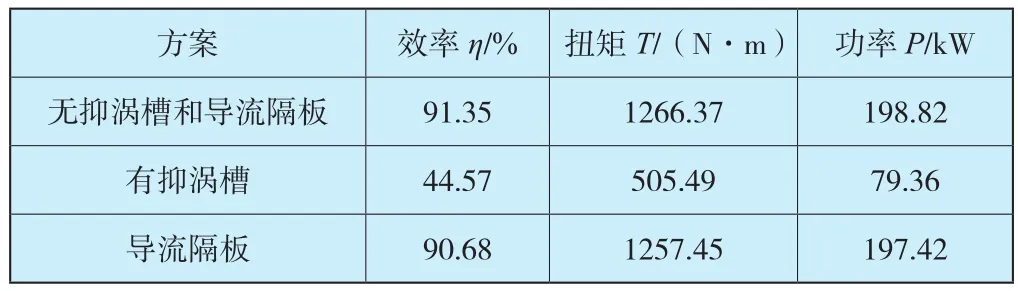
表8 不同方案下机组性能参数对比Table 8 Comparison of performance parameters under different schemes
3 结论
基于FBM湍流模型,选择五个不同流量工况进行非定常数值模拟,研究了不同流量与空化系数下尾水管涡带形态的演变规律,分析了尾水管涡带诱发低频压力脉动的特性,并针对抑涡槽和导流隔板两种优化措施对尾水管内部流场和压力脉动的影响做了具体考察。基于本文研究结果,可得到以下结论:
(1)尾水管涡带在不同工况下形态差异较大,其形态受流量和空化系数影响较大,小流量工况下整体表现为螺旋涡带,大流量工况下为梨形或柱状涡带。
(2)空化对50%Qr与110%Qr两个流量工况的影响最大,在两种流量下尾水管内部流动更为复杂紊乱,涡带形态发生明显改变,整体表现为极不稳定,监测点存在着十分丰富的低频压力脉动信息。
(3)采用抑涡槽的方案可以有效改善尾水管直锥段的不稳定流动,使直锥段压力分布均匀,并降低压力脉动的比率较大;采用导流隔板的方案不仅能改善直锥段内部流态,同时使得水平扩散段旋涡消失,能在整体上降低尾水管内流体的圆周速度分量、涡带诱发的压力脉动幅值。
