基于灰色关联分析的雷达外测数据精度评估方法

蔡铤彬， 冯书兴， 张雪芹， 赵 越， 代佳玲

(1.63766部队， 西双版纳 666200； 2.航天工程大学太空安全研究中心， 北京 101416； 3.战略支援部队参谋部， 北京 100120)

当前，卫星入轨段的定轨工作主要由全球导航卫星系统(global navigation satellite system，GNSS)导航定位数据、外弹道测量数据共同计算得到，其中GNSS导航定位数据以其精确的测量能力和便捷性而备受青睐。文献[1]指出，利用精密单点定位(precise point positioning，PPP)技术可在低轨卫星定位应用中给出高精度定轨数据。然而，雷达外测数据作为定轨数据源，可以在GNSS导航定位数据失效的情况下作为保底手段完成火箭外弹道测量任务，因此提高雷达测量数据的定轨精度仍是需要重点研究的课题。

现阶段精度评估的主要做法是基于已经获取的精确测量轨道，通过比较测量数据残差给出测量等级。由于雷达外测数据同火箭实际轨道之间存在系统误差、大气折射误差、地球摄动误差等因素，因此，前人对于误差模型修正做了大量的研究工作。雷达设备的主要系统误差修正参数是基于文献[2]的常规标校方法来获得，但是该方法必须基于准确的误差修正模型和精确的标校塔坐标，适用于基础设施保障较好的测量设备。还有基于恒星星历进行标校修正的方法，但是该方法仅能修正轴系误差，对于距离误差无法进行修正。文献[3-4]提出利用卫星进行标校的方法，在已知精轨数据和测量值的条件下，能够利用系统误差修正模型推导出系统误差修正参数，适用于各种类型的测量设备，但也存在在同一修正模型情况下，卫星标校结果和常规标校修正结果相近，并不能有效提高测量精度，且解析结果容易产生奇点。文献[5-6]提出基于轨道动力学约束和EMBET(error model best estimate of trajectory)算法的标校技术，并通过仿真取得了较好的精度评估效果。

以上的方法都是基于解析法获得的数据，对于模型的精确性、数据来源的多样性都提出了较高要求。但是对于单测站雷达设备而言，其测量数据十分有限，可利用的修正模型并不能完全消除误差，故如何有效利用少量的测量数据来评估设备测量精度是一个十分重要的研究问题。针对少量的雷达外测定轨评估数据，结合灰色系统理论的研究对象是“部分信息已知、部分信息未知”的“小数据”“贫信息”不确定性系统[7]这一特点，研究雷达外测数据与精轨数据评估的灰色关联性，并结合半监督学习方法，提出一种可靠的雷达测量数据精度评估方法，并基于“天平一号”卫星精轨数据给予验证。

1 灰色关联分析法在测量数据分析中的应用

灰色关联分析是灰色系统理论中一个十分活跃的分支，其基本思想是根据序列曲线集合形状的相似程度来判断不同序列之间的联系是否紧密，灰色关联理论认为，系统中任何两个行为序列都不可能是严格无关联的，若发展态势越接近，则关联程度越大。曹裕华等[8]从装备作战试验角度出发，基于灰色关联理论提出用于装备作战适用性的评估方法，并指出该方法不仅能对作战适用性进行合理有效的评估，还能对其影响因素进行主次关系分析。因此可以将误差系统统一看作“灰色”，则可将雷达测量结果同精轨数据直接进行关联计算。

设系统行为序列为

对于ξ∈(0,1)，令

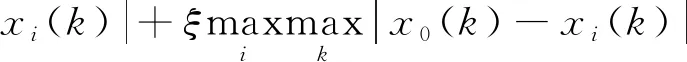
(1)

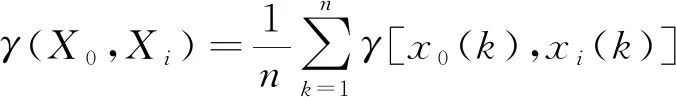
(2)

则γ(X0,Xi)满足灰色关联公理，其中ξ称为分辨系数；γ(X0,Xi)称为X0与Xi的灰色关联度。

对灰色关联度公式进行适当变化，可简化计算流程并获得更为详细信息，得到

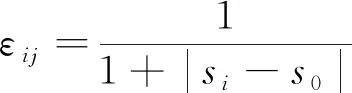
(3)

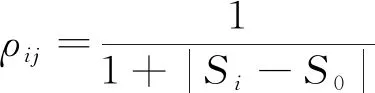
(4)

式中：

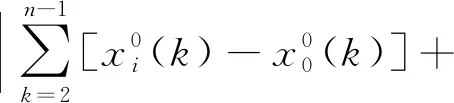
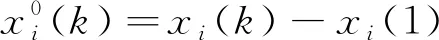
(5)

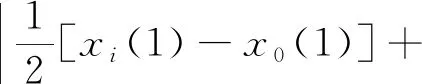
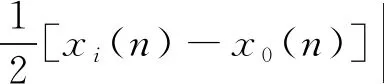
(6)

|si-s0|表示相似系数，相似关联度εij仅与X0与Xi的几何形状有关，与其相对空间位置无关，εij越大，X0与Xi越相似；|Si-S0|表示接近系数，接近关联度ρij不仅与X0与Xi的几何形状有关，还与其相对空间位置有关，ρij越大，X0与Xi越接近。

雷达外测数据可分为基于球面坐标系和基于直角坐标系两种表示方法，如图1所示，其中蓝实线表示球面坐标系，蓝虚线表示直角坐标系。在测量设备中，主要以球面坐标系(R,A,E)表示。

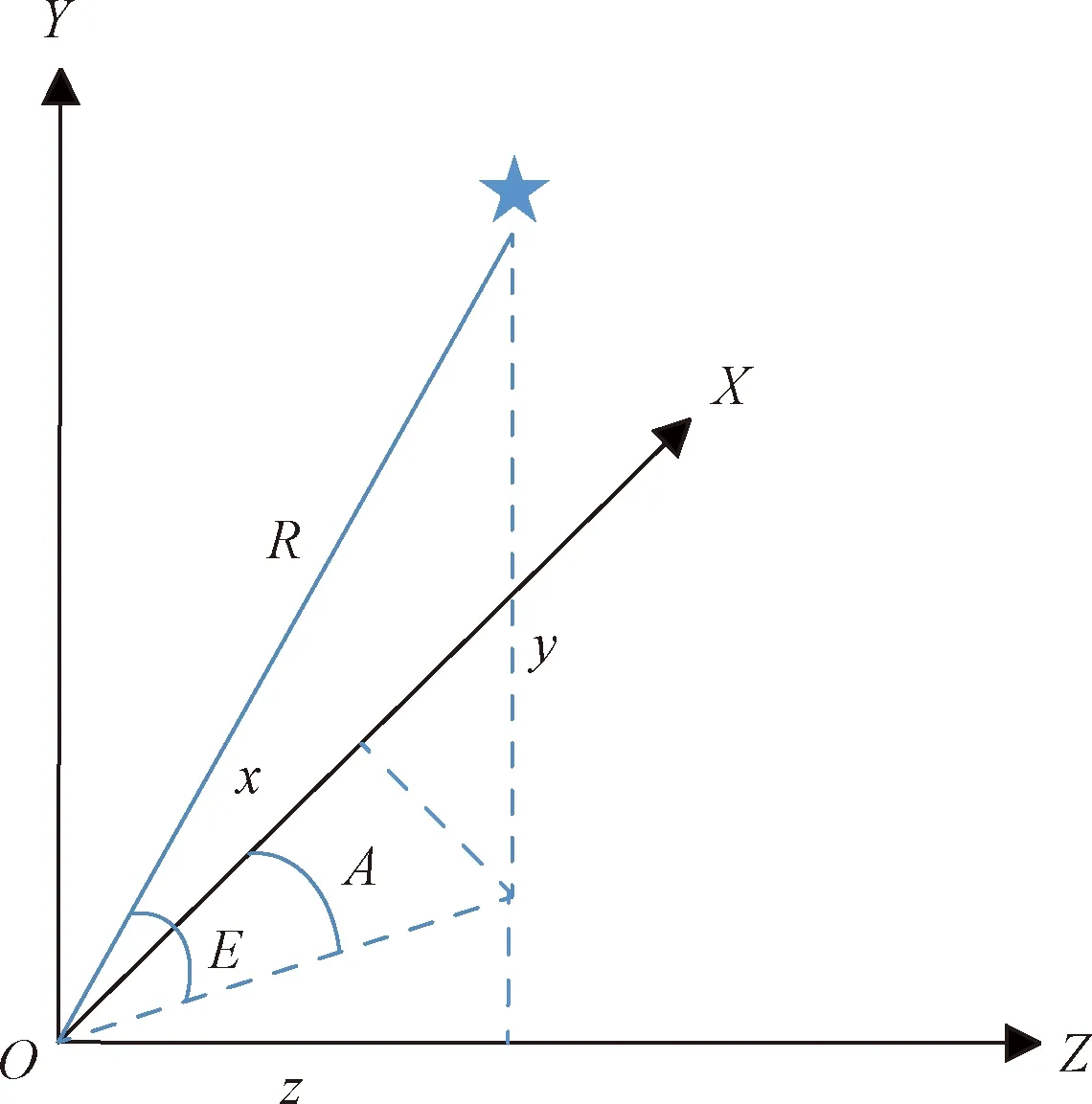
图1 球面坐标系和直角坐标系

由于精轨数据(R′,A′,E′)和测量数据(R,A,E)间不仅存在摄动、大气折射等因素的影响，还要考虑测量设备在测量高速运动的火箭、导弹或者卫星过程中存在动态滞后误差，因此相似关联度εij可以反映精轨数据与测量数据之间形状上的关联程度，接近关联度ρij还可以反映精轨数据与测量数据之间是否存在时延。

对某测量雷达的4次任务执行情况进行分析，由于定轨数据都是基于星箭分离时刻确定，灰色理论天然存在利用少量数据获取信息的优势。因此选用星箭分离前后共11点的时序数据进行处理；同时参照经验分析法，对设备进行大气折射修正后的测量值与精轨数据进行比较，为表现出跟踪效果与稳定性，采用偏差的绝对平均值与绝对标准差，获得结果如表1所示。

由表1可以看出，灰色关联度能从一定程度上反映整体上灰色关联度较好的测量结果，评价等级较高，但在绝对平均值和绝对标准差上区分度不明显。因此利用灰色关联度分析法评估外侧精度的方法是可行的。

除精度评估外，灰色关联度还具有对设备跟踪性能进行评估的效果。对于某测量雷达参加某次任务时，由于精轨数据与测量数据在时标上存在时延，对数据进行时延修正处理，结果如表2所示。从处理结果可以看出，通过对测量数据进行时延修正，精轨数据与测量数据在接近关联度上有所提高，尤其在R和A上提高明显，可以看出，通过计算精轨数据与测量数据的接近关联度和相似关联度，可以有效检验其测量结果是否存在时延。由于修正时延采用对测量值进行一阶差分的方法获取速度，修正精度不高，导致相似关联度存在部分变化，可利用更加准确的测量速度值进行修正，以提高关联。

另外，分析同一雷达设备执行4次任务的接近关联度和相似关联度，获得结果如表3所示。从表3中可以明显看出，该雷达每次任务的测量数据和精轨数据均存在良好的关联性，即该雷达的跟踪性能较好，但俯仰的接近关联度相对距离和方位结果较小，反映出该测量雷达在俯仰上存在明显的动态滞后，同实际装备维护过程中的现象相一致。

2 改进的灰色关联聚类方法

灰色关联分析法通过将误差系统转为“灰色”后对序列之间的关联性进行计算，可以较为准确地反映序列的接近程度。但是对于轨道测量，需要更为准确的评估方法来直观获得测量结果。从第1节的结论可以看出，单一指标的灰色关联结果并不一致，必须从整体上进行人为感官上的评价以确定精度评估效果，尤其对于数据较少的观测评估结果，其标准并不好确定。因此，可以利用灰色聚类方法实现综合评估，即不确定唯一标准值，通过关联程度进行结果评估。

聚类是试图将数据集中的样本划分为若干个通常不相交的子集(即“簇”)的方法[9]。文献[7]提出了利用绝对灰色关联度来获得两两指标组合之间的关联程度，通过设立阈值来实现聚类的方法。然而由于测量数据(R,A,E)和精轨数据(R′,A′,E′)之间仅有测量值，因此可以先计算测量数据和精轨数据之间的灰色关联度构成评价指标(γR,γA,γE)，而后再通过计算评价指标之间灰色关联度来获得两两测量任务之间的关联程度以实现聚类。为了保证测量结果既能够在相似性上一致，又能区分数值的大小，因此可通过计算评价指标之间的灰色接近关联度来提高区分程度。

表1 雷达测量数据灰色处理结果

表2 时延处理的灰色关联度比较结果

表3 任务数据接近关联度与相似关联度结果

然而文献[10]指出，当两两比较序列之间存在交叠时，即xi(k)≤xj(k)且xi(k-1)≥xj(k-1)或xi(k)≥xj(k)且xi(k-1)≤xj(k-1)时，其结果会导致两个不同形状的序列获得序列接近或相似的结果，究其原因，是因为文献[7]的方法中采用的式(3)、式(4)，在式(5)、式(6)的计算过程中，采用面积相加的方法，导致在序列交叠时，面积相互抵消，影响了结果的正确性。因此为了消除因序列交叠造成的影响，文献[10]对算法作出改进，即

当情形①xi(k)≤xj(k)且xi(k-1)≤xj(k-1)或xi(k)≥xj(k)且xi(k-1)≥xj(k-1)时

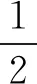
(7)

否则情形②

Si,j(k)=

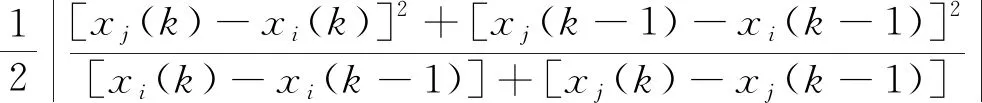
(8)

得到

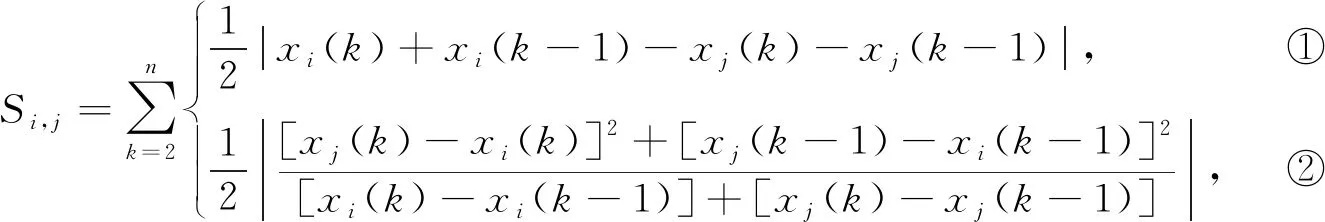
(9)

式(9)中：Si,j为改进后的接近系数，代入式(4)获取两序列间的改进接近关联度ρij。

计算某雷达4次任务的接近关联度，其上三角矩阵结果如表4、表5所示。

表4 刘氏接近关联度

表5 改进后的接近关联度

从计算结果可以看出，改进后的接近关联度更加符合实际指标的变化趋势，避免了将不一致的序列归为一致的结果，同时对于一致的序列，其关联度将更高。设关联阈值为0.875 0时，则任务2、3、4之间的关联度要优于任务1与任务2、3、4之间的关联度，即任务1为一类，任务2、3、4归为一类，这符合任务评级的结果。但是ρ1,3和ρ2,3之间的差值为0.008 6，极易受其他因素扰动，不适合区分出任务3与任务1和任务2之间的类别。考虑到实际上中心系统以直角坐标系O-XYZ表达卫星位置信息，因此将基于测量设备的球面坐标系O-RAE转化为基于测量设备的直角坐标系O-XYZ，通过计算(γX,γY,γZ)得到直角坐标系各个方向上的灰色关联度，而后在计算各任务间的接近关联度，结果如表6所示。

从表6中可以看出，将关联阈值设为0.9时即可区分子集，且任务1和任务2、3、4之间的关联度区分更加明显，ρ1,j的最大值为0.833 4，ρ2,j和ρ3,j的最小值为0.932 0，其差值为0.098 6远大于0.008 6。因此可以认为，将基于测量设备的球面坐标系O-RAE转化为基于测量设备的直角坐标系O-XYZ后，其灰色聚类结果更加符合实际任务的精度评估要求。

表6 O-XYZ直角坐标系下改进后的接近关联度

3 外测数据精度评估方法及应用

对于含有少量“有标记”样本和大量“未标记”样本的数据集，仅考虑聚类方法将会对“有标记”的信息造成浪费。因此，文献[9]指出可以考虑将学习器自动地利用未标记样本来提升学习性能，这就是半监督学习。

3.1 基于聚合聚类的半监督学习方法

第2节中通过灰色关联度获得了两两样本之间的接近程度，数值越大则接近程度越高，因此利用层次聚类法的聚合聚类法结合已知的有标记信息可以实现更加符合需求的分类。

聚合聚类开始将每个样本各自分到一类；之后将相距最近的两类合并，建立一个新的类，重复此操作直到满足停止条件，得到层次化的类别[11]。

用灰色接近关联度作为样本之间距离的表达方式，结合有限的标记信息，聚合聚类的算法可表示如下。

输入：n个样本组成的样本集合及样本直接的接近关联度。

输出：对样本集合的一个层次化聚类。

(1)计算n个样本两两之间的接近关联度{ρij}，记作矩阵D=[ρij]n×n。

(2)构造n个类，每个类只包含一个样本。

(3)合并类间关联度最大的两个类，其中最大关联度为类间关联度，构建一个新的类。

(4)确立新类与当前各类的关联度。若类的个数为1或标记的不同类信息之间关联度最大，终止计算，否则回到步骤(3)。

第2节O-XYZ直角坐标系下改进后的接近关联度为例，其计算结果如图2所示。从图2可以看出，经过聚类，任务3和任务4先聚类，而后又与任务2聚类，最后和任务1聚类。由于任务1标记为乙级，任务2、3、4为甲级，因此类7的聚类被终止，得到两类{任务2，任务3，任务4}和{任务1}，该聚类方法符合实际结果。

3.2 基于标校星的外测数据精度分析应用

由于机动设备的标校场地往往较为简陋，常规标校参数受外界环境影响较大，为了在任务前确保设备精度符合要求，可以考虑通过标校星进行跟踪验证，利用灰色关联分析和聚合聚类结合的方法对设备跟踪精度进行评估。

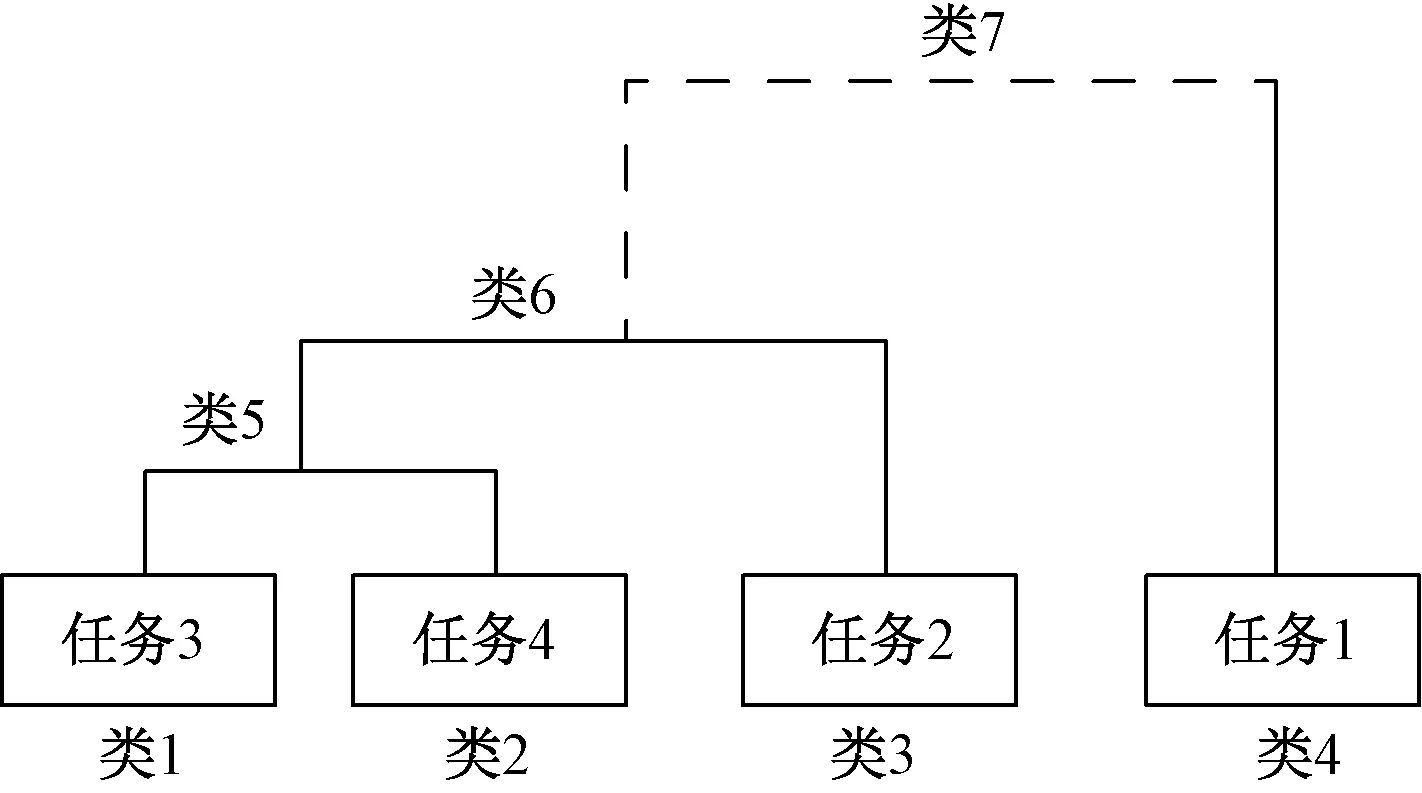
图2 基于接近关联度的聚合聚类结果

“天平”一号卫星是中国首颗天基标校卫星，当前在轨运行良好且定位精度符合标校要求。利用某测量雷达跟踪“天平”一号的7组测量数据和精轨数据，结合4次任务执行数据，可获得其灰色关联分析结果，如表7所示。

表7中，1代表任务1，2代表任务2，3代表任务3，4代表任务4，5代表天平1，6代表天平2，7代表天平3，8代表天平4，9代表天平5，10代表天平6，11代表天平7。将有标记和未标记的数据集进行聚合聚类，直至甲级数据和乙级数据关联度最大停止，得到结果如图3所示。

从图3可以看出，聚类结果为{任务2，任务3，任务4，天平1，天平2，天平3，天平4，天平5，天平6，天平7}和{任务1}，由于任务1为乙级，任务2、任务3、任务4为甲级，因此可以判定天平1-7的跟踪精度均为甲级，其标校结果用于任务中均符合跟踪要求。

若精度评估结果仅和任务1聚类，或者与甲级、乙级标记均不能聚类，则判定该雷达精度不符合要求，对于该标校参数应重新测定后再进行验证，直至结果符合甲级评定要求。

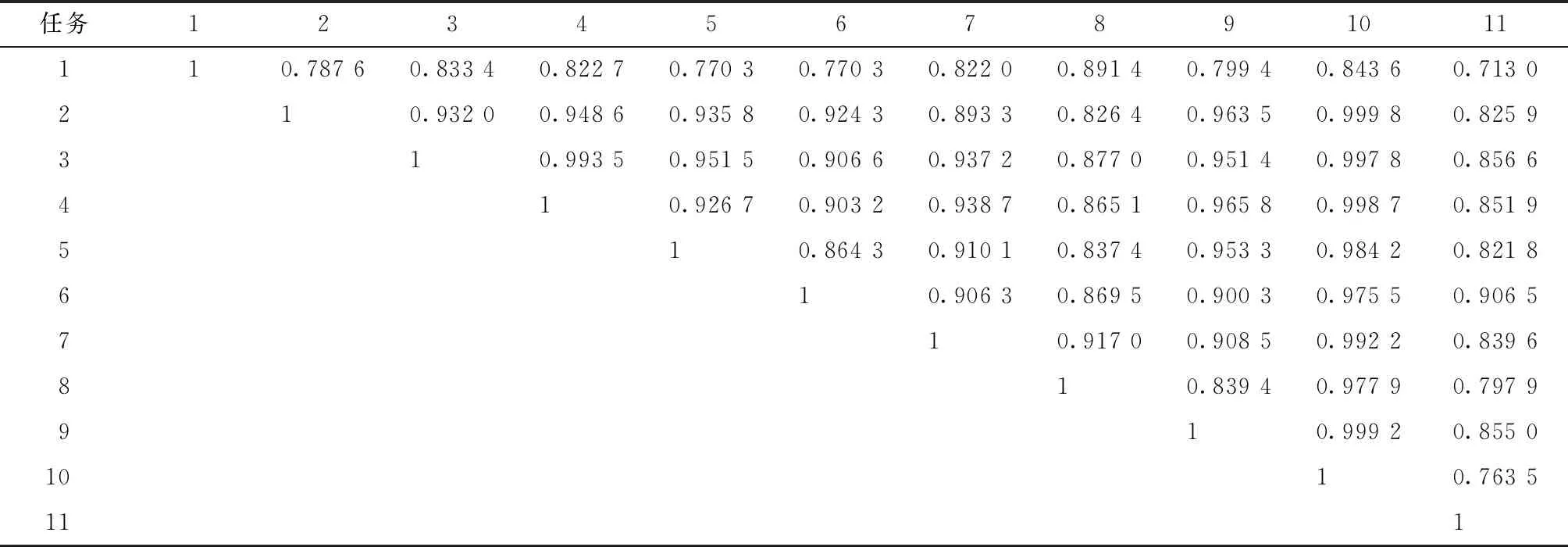
表7 接近关联度上三角矩阵

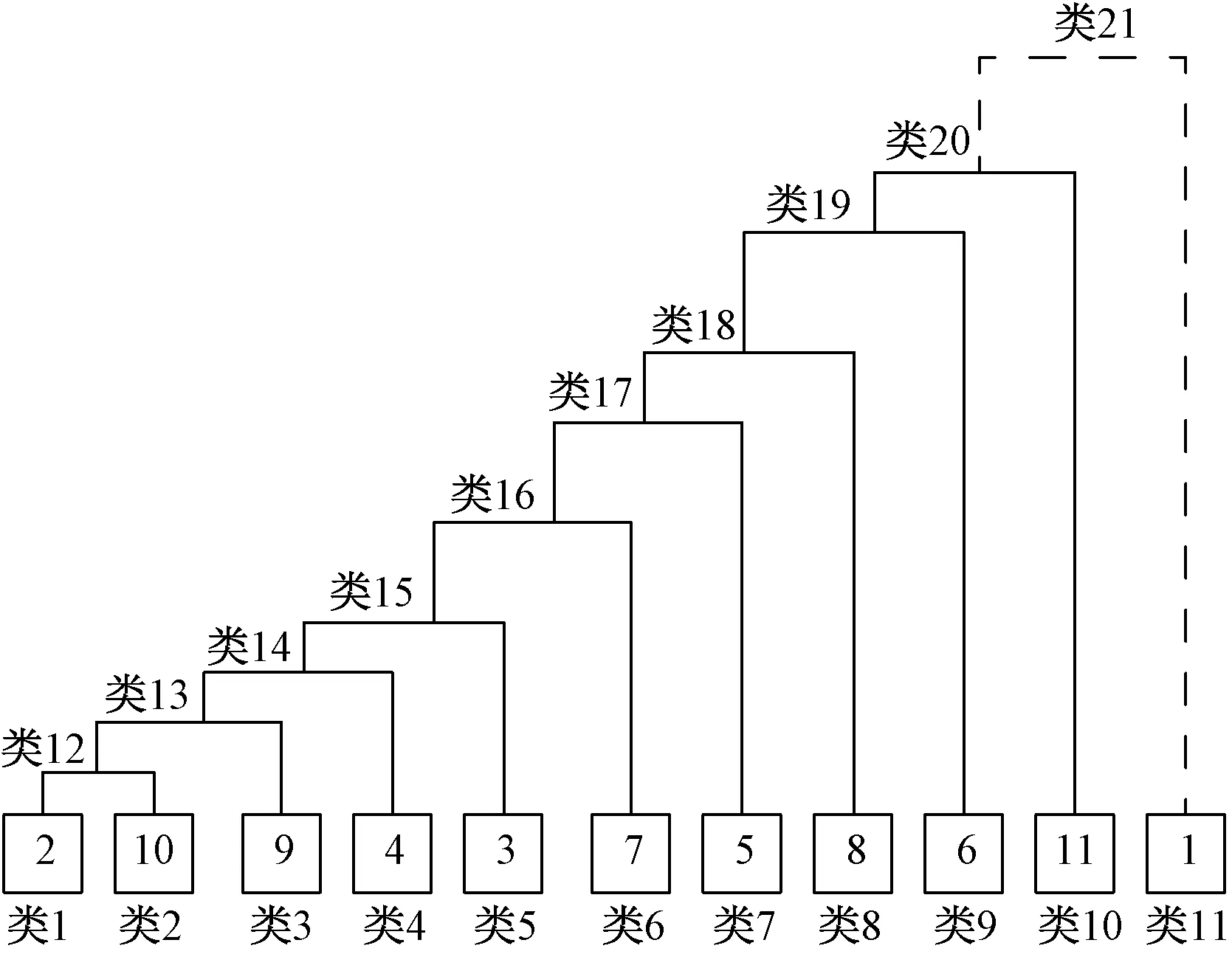
图3 基于接近关联度的“天平”一号卫星聚合聚类结果

4 结论

通过研究雷达外测数据中的精度评估方法，提出了利用改进的灰色关联分析法结合半监督学习来分析雷达外测精度的方法，利用有限的含标记与未标记的数据，得到对雷达外测数据评估更加准确可靠的结论，符合实际应用中的评估效果，并在某型号雷达设备跟踪“天平”一号卫星的跟踪结果中得到了验证。该方法可剔除误差系统带来的影响，简化评估模型，能够适用不同修正模型下的外测数据精度评估，为测量雷达在任务前利用卫星标校验证设备精度提供了可靠的参考方法。