基于图论模型的认知无线电频谱分配仿真建模研究

刘新浩 马昕睿 王大为

（山西师范大学物理与信息工程学院，山西 临汾 041000）

1 引言

无线通信不断发展壮大，但是目前可以合理分配的频谱资源较稀缺，对其需求却不断提高，频谱分配资源的短缺已经成为阻碍现代无线通信技术的一个重要问题。然而，有一些科学研究结果表明，传统的固定式频谱分配体制，存在着频谱分配不均，甚至浪费等不良现象，如美国联邦通信委员会（FCC）的大量调查结果显示，授权频谱利用率一般在15%~85%之间[1]。认知无线电技术，可在不对已授权频段用户通信造成影响的前提下，实现频谱分配的动态管理，使非授权用户机会式地利用游离的授权频谱资源，使频谱资源合理利用[2]。本文在图论模型的基础上,通过建模仿真提高认知无线电频谱分配利用率，以得到“频谱分配”的高效合理利用。

建模中，设置二维频谱可用矩阵L，其值为0或1，作为非授权用户n对于m频谱的可用情况。效益矩阵B为同行列数二维矩阵，其值为正实数，描述非授权用户在获得相应频谱后可得的网络效益。设置三维矩阵C(M个二维矩阵)，表示用户在同时使用频道m时的冲突情况，其值为1表示不同用户在使用同一信道时会产生干扰。终极频谱分配的策略将会储存在无干扰分配矩阵A。本文通过仿真建模将频谱分配最优化问题抽象成用户平均效益目标函数求最优解问题，实现频谱分配的最优化，解决频谱分配效益低的问题。

2 基于图论模型的认知无线电的模型建立

2.1 模型主要参数介绍

认知无线电网络主要由非授权用户、授权用户和认知基站共同构成[3]。建造认知基站方便实现了授权与非授权用户之间的实时通信，在不对授权用户造成不利影响的情况下，非授权用户也可以使用该授权频段，且在实际通信的环境中，授权用户和非授权用户均可能会因外界各种因数而发生动态的变化。本文考虑在极短的时间以至于该时间范围内信道环境保持恒定不变的情况。信道环境参数大致包括效益矩阵B，频谱可用性矩阵L，干扰分配矩阵C，无干扰分配矩阵A。设置在通信环境中允许可用的频谱数为M,非授权用户数量为N，以下对环境参数简单介绍[4]：

（1）将频谱效益矩阵B设置为N×M二维矩阵，B={bn,m|bn,m∈R+}N×M，bn,m取正实数，其值可用于表示非授权的用户n在获得频谱m后可以带来的网络效益。

（2）频谱可用性矩阵L同样为N×M二维矩阵，L={ln,m|ln,m∈{0,1}}N×M，若ln,m=1则认为信道m可对于非授权用户n使用。

（3）干扰约束矩阵C为用户在第m个频段上的冲突情况，设置M个N×N构成的三维矩阵C={cn,k,m|cn,k,m∈{0,1}}N×N×M，在各二维的矩阵中，cn,k,m=1表示授权用户n和授权用户k会在同时使用信道m时造成干扰；cn,k,m=0则表示无干扰。

（4）无干扰分配矩阵A也看作N×M的二维矩阵，A被用来保存某时段M个频谱对N个非授权用户的最后分配策略，其一般的形式为A={an,m∈{0,1}}N×M，an,m=1表示频谱m在该时段对n可用。但需特别注意，无干扰分配条件是无干扰分配矩阵才有意义的必要条件。

2.2 解空间的压缩

频谱分配最优结果是通过无干扰分配矩阵A进行记录，对A直接编码，其中对于维数N×M的编码难度较高。因A在可用性矩阵L的控制下，值为0的元素所对应A的元素必然为0，因此我们只要从其中提取出值为1的元素实行编码[5]，优化完成后再按照其相应的关系进行还原。例如图1，L为4×4二维矩阵，经过简单地缩减后成为一个1×4一维矩阵X，解的维数由16缩减为4，搜索空间由216降低成24，有效地降低了解空间的复杂度。

图1 解缩减实例

2.3 建模算法

无干扰矩阵受可用性矩阵约束，将L中为1的元素提取编码，优化后根据对应关系还原便可，基于该原理可用设计认知无线电建模算法并缩减其解空间，最终实现频谱的最优化分配。

基于图论模型的认知无线电频谱分配流程图如图2所示。

（1）生成可用频谱矩阵L和干扰约束矩阵C，其中L和C维数已确定，但取值未必合理，故调整保证取值符合要求如图2所示。

（2）求压缩后的L，缩减解空间，降低编码难度如图3所示。

（3）求压缩后的干扰约束矩阵C，其中第i列储存的是和xi不能同时使用同一信道的用户信息如图4所示。

图2 产生合法L和C

（4）根据缩减后的可用频谱矩阵，使其对应缩减前对应位置元素1的效益，可得缩减后的效益矩阵B如图5所示。

得到基于图论的认知无线电频谱分配算法如下所示：

%%产生L和C

1返回L矩阵信息

2 while（sum（L）==0）

3生成L矩阵，保证有可用信道

4 end

5 for i=1：M

6生成M个信道的干扰约束矩阵

7 for j=1:N

8 自干扰

9 end

10 for p=1：N

11 for q=1：p

12 互干扰

13 end

14 end

15 end

%%缩减解空间

16保存缩减前后解的映射关系

17确定空间维数

18存放L中1的坐标

19保存缩减后L和原L的映射关系

%%求压缩后的C

20压缩后L的页数

21求压缩后的L中第i个和第j个元素之间存在的干扰条件

22 if同一个信道可分配给两个用户且两个用户同时使用该信道会存在干扰

23列数i和每列元素不能同时使用一个信道

%%求压缩后的效益矩阵

24初始化压缩效益矩阵

25 for i=1:1：Dim

26储存L中为1元素对应的效益

27 end

28 end

3 仿真实验与分析

为探究基于图论的建模仿真可以优化认知无线电频谱分配，以提高频谱利用率。通过建模仿真，对最大网络总效益和不同认知数和频道数下平均效益分析研究。其中环境参数L、B、C、M、N设置为：随机生成的0、1矩阵L；B元素为实数，大小可从1-10随机选取；C中各二维矩阵是随机生成的0、1二元对称矩阵；IBPSO算法参数设置同文献[6]：种群大小SN=20；c1=c2=4;δ=2，最大的迭代次数设置成1000。

3.1 最大网络效益比较

假设信道环境在极短时间内不发生改变，频谱分配可将最大网络效益作为目标函数。本文以IBPSO算法在图论模型认知无线电频谱分配模型下仿真，在分别仿真30次后得到了平均网络总效益的收敛曲线如图6所示。

图3 缩减解空间

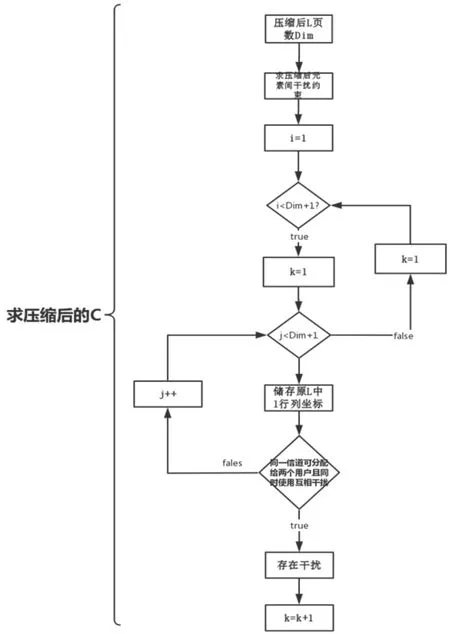
图4 压缩后C

图5 压缩后B

图6 平均网络总效益

由IBPSO算法对于平均效益的收敛曲线分析可以清楚地看到，IBPSO算法取得了较好的寻优效果，保证了在进化过程中各个种群的连续性。说明了图论模型下认知无线电频谱分配建模可以得到较好的寻优效果。

3.2 不同用户数下的平均效益

在可用频谱数M恒定为30，认知数逐渐增加时，仿真得到图7。可以看出，伴随认知数增加，平均每个认知用户所取得的平均效益总体上呈递减的变化。可见通过图论模型的无线电建模与实际的频谱分配时的平均效益相符合。

3.3 不同信道数下的平均效益

设仿真中认知用户数N恒定为20，可用频谱M的增加，得到单个用户获得的平均效益如图8所示，可看出伴随可用频谱数的逐渐增加，单个用户已经获得了较好的平均效益。

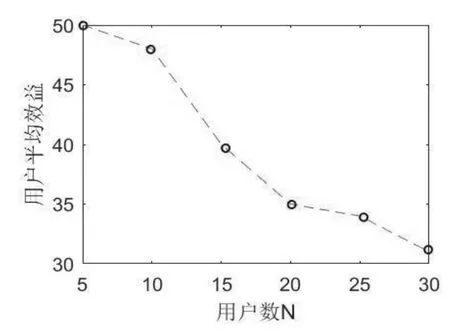
图7 N增加时的平均效益

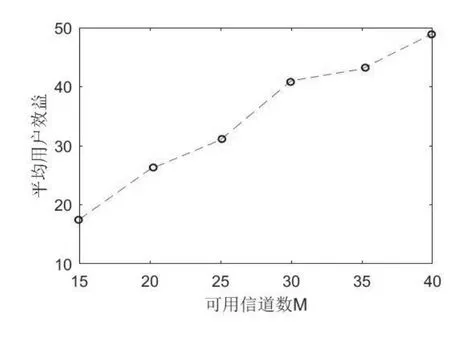
图8 M递增时的平均效益

4 结束语

优化频谱分配，提高频谱利用率是当前无线通信必须解决的问题之一。频谱分配模型类似N-Hard约束优化问题[7]，通过图论模型下的仿真建模可以有效协助解决频谱分配最优化问题。本文提出了解空间的压缩方法，可很大程度上降低矩阵编码难度，大大缩减解空间，还原时只需根据压缩前对应关系填充即可。在进行仿真实验与分析时，借鉴IBPSO算法，通过对平均网络总效益以及在不同的认知用户数和信道数下的平均效益进行分析，验证了基于图论的建模仿真能够优化认知无线电频谱分配问题。实验表明，基于图论的认知无线电频谱分配仿真建模研究有利于优化频谱分配，解决当下频谱资源紧张问题。