考虑成员主导行为的闭环供应链定价决策研究

韩 冰 徐梦诗

（河南牧业经济学院物流与电商学院 河南郑州 450044）

一、引言及文献综述

网络购物的普及助推了快递业迅猛发展。随着快递行业的快速发展，许多问题也随之而来，其中最显著的问题之一便是快递包装的回收处理问题。

在快递包装回收再利用方面，国内外已有大量成果。刘国秋等人（2014）在循环共生经济理念的指导下提出了快递包装逆向物流回收的四种模式，通过信息反馈、物流成本和适用企业这三个方面的比较得出了这几种模式之间的差别；姚连杰（2019）充分考虑回收活动中政府的作用，建立了三种政府规制下的快递包装回收模式；罗媛静等人（2015）考虑包装的绿色设计和使用后的回收问题，将目前三种主流的回收模式相结合，实现包装废弃物逆向物流网络高效运作；乐雄平（2016）分析了以垃圾回收站、包装生产商、第三方物流企业为主导的三种快递包装逆向物流回收模式的优势与不足之处，并提出了另一种的回收模式——自营物流回收模式；廖成林等人（2011）构建了整数规划模型，通过算例分析来研究快递包装回收问题并提出优化策略。

二、模型描述及基本假设

（一）问题描述与基本假设

本文建立了一个由快递包装制造商和快递企业组成的两级闭环供应链系统（Closed-loop Supply Chain，CLSC）。

其中，快递包装制造商主要负责生产新的快递包装以及处理回收的废弃快递包装。快递企业的任务主要是从快递包装制造商处购买快递包装，同时通过现有的快递网点将废弃的快递包装从消费者手中回收，然后卖给快递包装制造企业。快递企业可通过支付一定的报酬来提高消费者的回收积极性，从而提高快递包装的回收量。本文假设由原快递包装制造商处理回收的快递包装。

本文采用Stackelberg博弈模型研究快递包装回收问题，考虑闭环供应链成员的主导行为，以成员自身利益最大化为决策目标研究快递包装定价决策。为了研究方便，本文模型做出如下假设：

H1：在闭环供应链上快递包装制造商和快递企业掌握的信息是对等的，且二者都是完全理性的，是为了谋求自身利益最大化而进行作业。

H2：快递包装的潜在需求量是固定的，需求量为D(p) ，其中p是快递包装的零售价格，m为市场总容量，n为市场需求的零售价格敏感程度。快递包装的价格越高，快递包装的需求量就越小。因此 D(p)=m-np，m，n为常数，且m＞0 ，n＞0 。

H3：快递企业对消费者的废弃快递包装回收价格为C1，则快递包装回收数量函数 Q(C1)=α+βC1（常数α＞0 ，β＞0），其中α为消费者的环保意识，即消费者在无偿的情况下愿意主动返还的废弃快递包装的数量，β为消费者对回收价格的敏感程度。

H4：回收的快递包装数量Q均为可以重复利用的快递包装数量，不存在不能使用的部分。

H5： H为快递企业回收快递包装的成本，令H(C1) =（1-k）Q2(C1) ，k为废弃快递包装的新旧系数，k越大说明快递包装回收成本越低。

H6：C1为快递企业向消费者支付的回收价格，C2为快递包装制造商向快递企业支付的回收价格，C3为快递企业在回收过程中赚取的差价，那么C2=C1+C3（C2＞C1）。

（二）基本参数

涉及的参数如下：

p ——快递企业销售快递包装单位零售价格

A——快递包装的批发价格

Cn——制造新的快递包装的单位成本

Cr——再制造快递包装的单位成本

C1——快递企业向消费者支付的回收价格

C2——制造商向快递企业支付的回收价格

C3——快递企业回收快递包装赚取的差价

D——市场上快递包装潜在需求量

Q——快递包装回收数量

H——快递企业回收快递包装的成本

τm——快递包装制造商的利润

τc——快递企业的利润

τ——整条供应链的总利润，且cτ=τm+τc

三、模型求解

（一）集中决策模式

集中决策模式就是将供应链上的快递包装制造商与快递企业捆绑为一个整体，在此模型中，快递包装制造商与快递企业所做的决策都是为了使整条供应链的利润最大化。其利润函数如下：

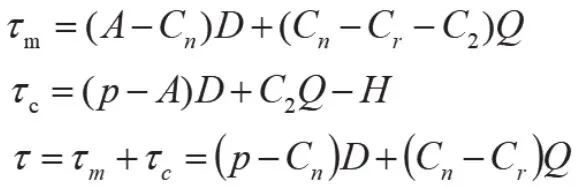
即：

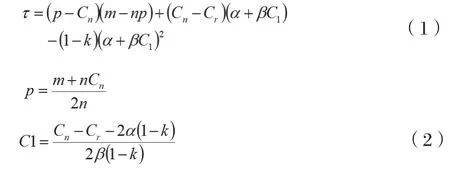
将式（2）代入式（1）得到在集中决策模式下闭环供应链的利润为：

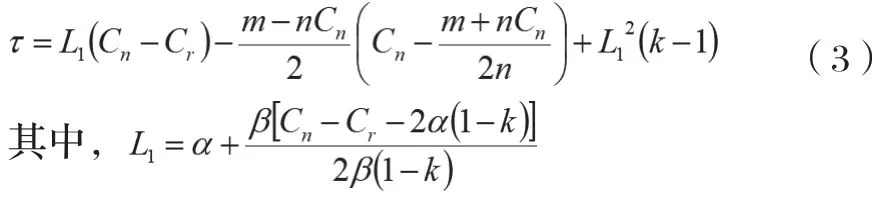
（二）包装制造商主导模式

本文主要描述的是在没有政府参与情况下，快递包装制造商与快递企业之间的Stackelberg博弈，快递包装制造商在博弈中占主导地位，快递企业作为跟随者而存在。快递企业在快递包装制造商做出决策时，在谋求自身利益的最大化的前提下跟随它的决策采取自己的行动。快递包装制造商的利润函数表示为：

快递企业的利润函数表示为：

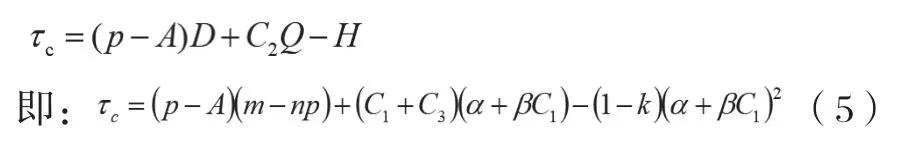
求解可得：

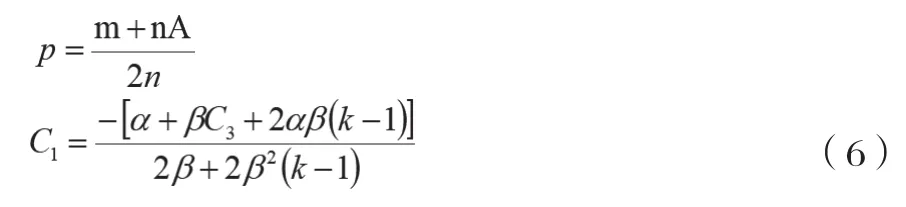
公式（6）表示快递包装制造商确定批发价格 后，快递企业根据批发价格决定最优零售价格以及从消费者手中回收快递包装的最优价格。

将式（6）代入式（4）得：

（7）

求解可得：此时，快递包装制造商可以获得最大利润。将式（8）代入式（6）得：

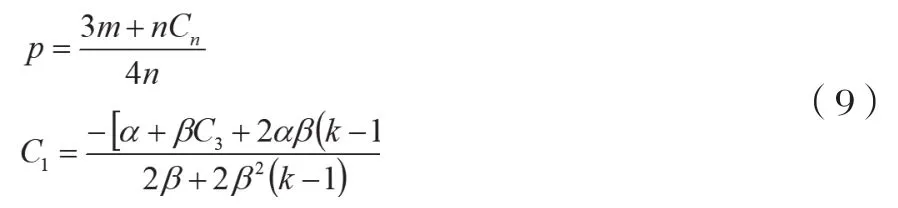
因此得出的Stackelberg均衡解为：

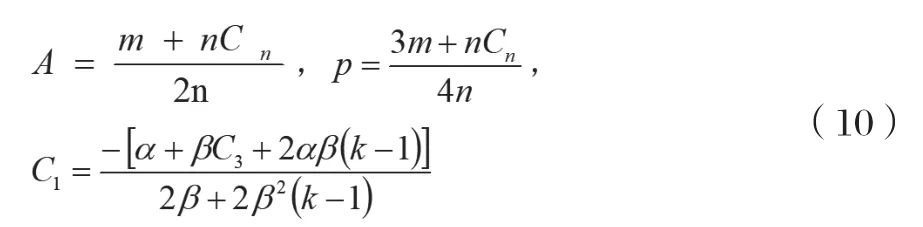
将式（10）代入式（4）、式（5）得到在Stackelberg均衡情况下快递包装制造商以及快递企业的利润：

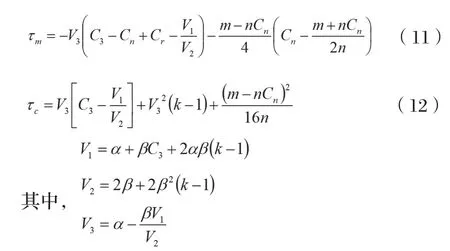
那么整条供应链的利润为：

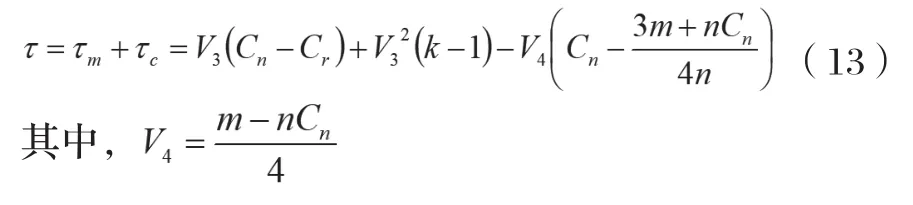
（三）快递企业主导模式

在快递包装制造商与快递企业组成的二级闭环供应链中，快递企业也可以在回收过程中占主导地位。在这种情况下，快递包装制造商跟随快递企业的决策而采取自己的行动。此时由于快递企业处于主导地位，因此快递企业会在批发价格的基础上将零售价格提高到p。其中，p=A+s(s＞0)。

快递包装制造商的利润函数为：

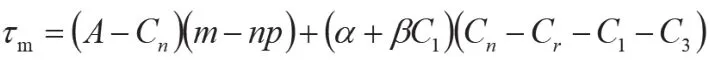
即：

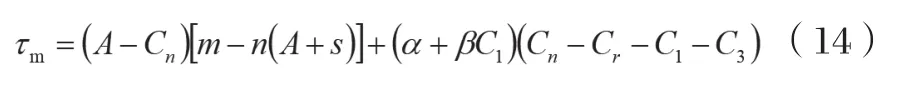
快递企业的利润函数为：

求解可得：

将式（16）、式（17）代入式（15）：

求得：

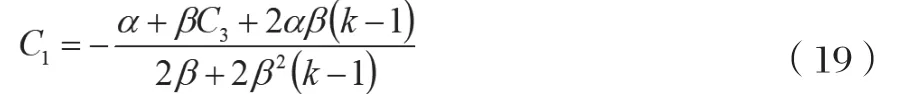
因此得出的Stackelberg均衡解为：

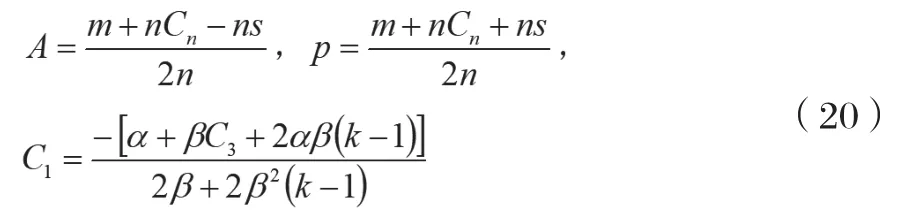
将式（20）代入式（14）、式（15）得到在Stackelberg均衡情况下快递包装制造商以及快递企业的利润：

整条供应链的利润为：

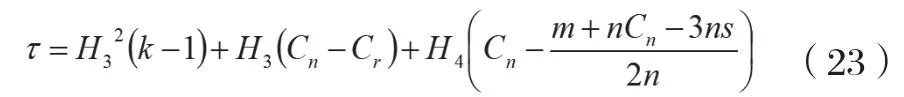
（四）均衡解分析结论

对比分析不同情形下的均衡解，可得以下结论：

第一，集中决策定价模式下的闭环供应链整体利润大于快递包装制造商主导模式与快递企业主导模式下闭环供应链的利润。这表明供应链上的企业只有加强彼此间的合作，才能获得整体效益的最大化。

第二，快递包装制造商是主导者时，快递包装制造商利润大于快递企业的利润；当快递企业为主导者时，快递企业的利润大于快递包装制造商的利润。这表明在闭环供应链中哪个企业占据主导地位，该企业就能在决策中获得更大的利润。

第三，快递企业的利润与快递企业通过回收赚取的差价关系密切，s在逐渐增大的过程中，快递企业的利润先是渐渐增高，但随着s的变大，快递企业的利润会逐渐减小，而快递包装制造商的利润则随着s的减小越来越低，并且随着s的逐渐增大闭环供应链的整体利润就越低。

四、算例分析

（一）数值仿真

为更好的运用Matlab数据仿真软件对快递包装进行算例分析，本文通过数值算例来比较不同决策模型的均衡解，以进一步探讨主导模式对于闭环供应链产品定价以及节点成员利润的影响，具体数据：Cn=2.1 （元/件），Cr=1.1 （元/件），C3=0.37 （元/件），s=2.4 （元/件），m=55 亿件，n=8 ，α=0.3 亿件，β=4 ，k=0.6。

将上述数据代入求解模型得到最优解如表1所示。

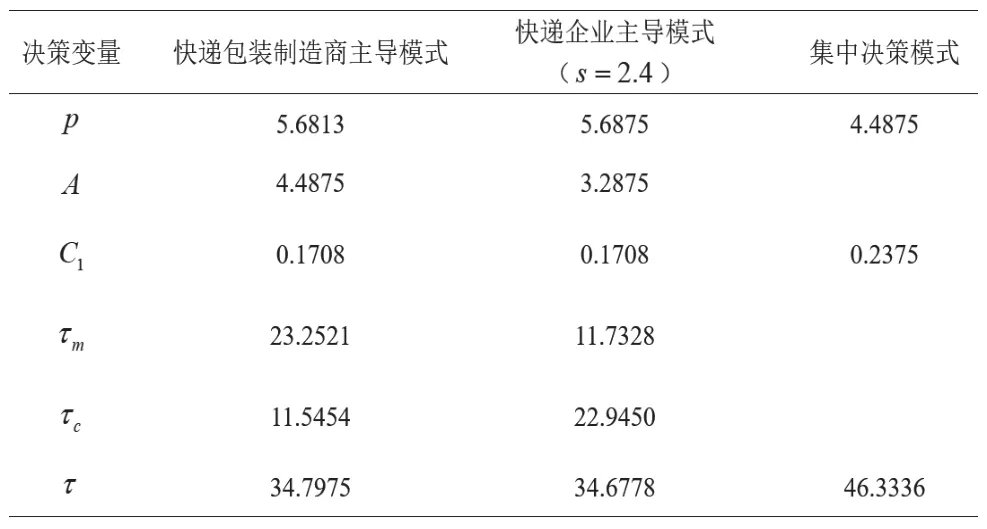
表1 三种模式下的定价比较

（二）分析总结

根据算例仿真可以得到以下结论：

第一，集中决策定价模式下的快递包装零售价格为4.4875，快递包装制造商主导模式下快递包装零售价格为5.6813，快递企业主导模式下快递包装的零售价格为5.6875，由此可见，集中决策定价模式下快递包装的销售价格更低，更有利于快递包装的销售。

第二，集中决策定价模式下的回收价格为0.2375，快递包装制造商主导模式与快递企业主导模式下的回收价格均0.1708，集中决策定价模式下的回收价格明显更更高的回收价格能够更好的促进消费者参与回收活动，快递包装的回收量也会随之增加。

五、结论

本文在闭环供应链系统中考虑了成员的主导行为，分别在集中决策定价模式、快递包装制造商主导模式以及快递企业主导模式这三种情况下研究了快递包装制造商、快递企业以及整个闭环供应链的最佳定价策略以及最优利润。通过综合比较可知，集中决策定价模式能够使闭环供应链利润最大化。快递企业与快递包装制造商之间的利润关系和快递企业在回收活动中从中赚取的差价关系密切，快递企业所获得的利润也与回收差价密切相关。