沥青混合料空隙特性分析及多重分形研究

2021-05-13吕悦晶刘标张蕾汤文

中外公路 2021年2期

吕悦晶，刘标，张蕾，汤文

(1.武汉科技大学汽车与交通工程学院，湖北武汉 430065； 2.交通运输部公路科学研究院)

沥青混合料在拌和、摊铺、压实过程中，集料、沥青、空气三相无法完全黏结，会产生初始空隙。初始空隙会弱化路面结构进而损害路面层最后影响路面使用性能，可见空隙在路面损伤中有不可忽视的作用。因此空隙研究对提高沥青混合料的结构性能，提升路面性能及提高路面养护质量具有重要的意义。

国内外学者对空隙的研究已经发展到从细观尺度表征空隙特性。张倩等、吴文亮等结合CT扫描试件与Matlab技术，证明空隙率随层位呈两端大中间小的分布趋势；Arambula等采用CT和数字图像技术研究沥青混合料试件在不同深度范围内的空隙分布，并评价沥青混合料空隙分布与水稳定性的关系；Tashman等研究沥青混合料的空隙分布状态，并获取集料相关特性等微观结构参数，证明沥青混合料的微细观结构对宏观性能有影响；谭忆秋等利用CT技术，优化相关参数，验证细观计算空隙率与宏观空隙率具有良好的相关性。

上述学者从细观尺度证明空隙率沿试件高度具有两端大、中间小的分布规律，并表明微细观结构与宏观结构具有一定关联性，具有研究指导意义，但缺乏空隙结构特性与几何形态研究。包秀宁等对不同空隙结构的沥青混合料进行水损害试验，结果表明：不同空隙结构抗水损害性能不同；张志辉等建立不同空隙结构沥青混合料模型，模拟受力分析，结果表明：空隙结构不同，荷载应力增长速率不一致；包秀宁、张志辉从空隙结构方面研究空隙结构对混合料结构性能的影响，但缺少空隙形态方面的研究；裴建中等、颜强等提出用分形维数表征空隙轮廓方法，结果表明：空隙率越小，空隙轮廓分形维数越大；蒋玮等证明分形维数能反映混合料断面图像空隙结构的复杂程度，断面空隙图像分形维数越大，混合料中空隙通道越复杂；裴建中、颜强、蒋玮用分形维数对空隙结构和空隙轮廓进行了研究，但没有定量表征空隙形态特性，且缺乏对空隙多尺度的研究。

综上，众多学者从空隙率分布、空隙结构、空隙轮廓等方面对沥青混合料中空隙开展大量相关研究，但缺乏对混合料空隙形态特性定量表征和空隙复杂结构多尺度研究。该文提出平均长轴、平均短轴定量方法表征空隙形态信息，采用多重分形的谱参数多尺度表征局部空隙结构，进而从细观尺度方面充分刻画出空隙特性的丰度。

1 混合料试验及图像分析

1.1 试件成型

试验按照规范成型AC-13型沥青混合料标准马歇尔试件(直径101.6 mm，高度63.5 mm)，采用70#沥青，集料选择石灰岩。沥青基本性质测定试验按照JTG E20-2011《公路工程沥青及沥青混合料试验规章》(简称《规程》)进行，测量指标见表1。试验所采用的沥青混合料为粒径4.75 mm、通过率为34.8%的密实-骨架型混合料结构，级配如表2所示。

表1 沥青基本性质

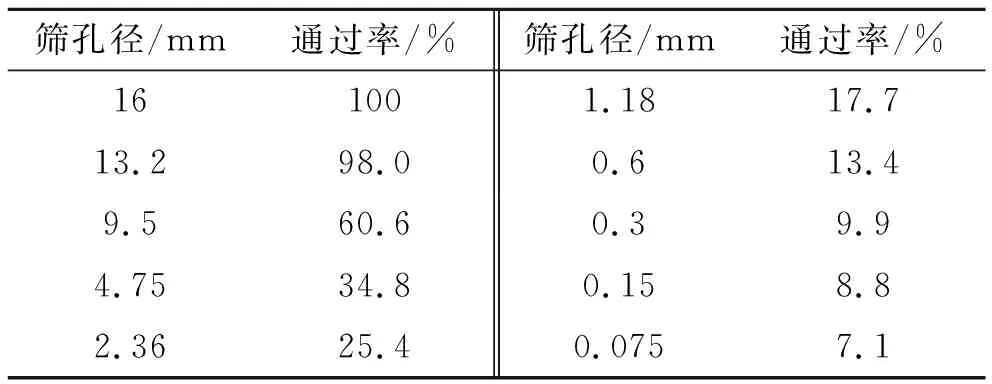
表2 AC-13沥青混合料级配

1.2 试件芯样CT扫描与数字图像处理

CT(计算机断层扫描)是一种X射线辐射成像技术，试验采用工业320 kV CT扫描设备。根据预试验结果，试验采用的扫描间隔设定为0.1 mm，得到有效CT图片635张。沿试件深度的中上部、中部、中下部、下部4个层位选取连续2张空隙特征明显的CT图片进行研究，即中上部、中部、中下部、下部都有连续2张CT图片，连续2张图片中有1张图片位于上面，另一张图片位于下面，位于上面称为上层图片，位于下面称为下层图片，且将中上部、中部、中下部、下部4个层位上层图片分为上层组，下层图片分为下层组。

提取空隙过程中，CT图像中集料灰度最高，沥青胶浆其次，空隙最小，且集料与沥青胶浆、沥青胶浆与空隙的灰度范围有一定重合。因三相材料组分灰度范围重叠，选用局部阈值法分割图像，阈值分割后运用开、闭形态学算法将空隙从集料和沥青胶浆中清晰提取出来，然后二值化图像，二值图中白色为空隙，黑色为集料、沥青胶浆。如图1所示。

图1 原图与二值图

1.3 空隙参数提取及统计特征分析

几何形态是空隙的重要特征属性，鉴于长、宽直观数学含义，将空隙拟合成椭圆，用长轴与短轴表征空隙形态(图2)。在图2(b)中选取形态特征对比明显的1号、27号空隙来说明形态变化特征。1号、27号椭圆的长轴、短轴信息如表3所示。

图2 空隙图形拟合示意图

表3 局部空隙长轴、短轴

表3中两椭圆长、短轴差不为零，长轴与短轴不等，说明两椭圆不是圆形，且1号椭圆长、短轴差比27号椭圆大，说明1号椭圆长轴更长，形态更扁平，空隙上表现为狭长形态，而27号椭圆长轴较短，形态更趋于圆形，空隙上表现为聚集形态。两椭圆长轴差、短轴差值进一步证明1号椭圆扁平明显即空隙狭长形态特征明显，27号椭圆类圆明显即空隙聚集形态特征明显。因狭长空隙，具有更多凸起和凹陷部分，形态上狭长空隙比聚集空隙更为复杂。

混合料中空隙狭长程度越高，混合料的裂纹扩展可能性越大，抗劈裂性较低；空隙聚集程度越高，竖向空隙空洞集中程度越高，对混合料受力荷载性能影响较大；空隙形态呈现狭长状与聚集状，对路面结构强度与路面裂纹扩展的可能性会不同。因此研究空隙形态对沥青混合料的力学性能和路面破坏有一定的指导意义。

基于上述空隙研究，将局部空隙研究延展到整个层位断面，提出平均长轴与平均短轴概念，用平均长轴与平均短轴定量表征断面空隙整体形态，分析断面平均长轴与平均短轴变化，推断断面整体空隙形态，进而表达断面中空隙的复杂程度。

在image pro plus中对图像进行尺寸标定，标定试件直径为101.6 mm，提取断面中空隙总面积、拟合椭圆总长轴、拟合椭圆总短轴、有效空隙个数等信息。令图像空隙总面积为S0，试件横截面面积为S1，试件直径D=101.6 mm，横截面面积由式(1)求得，定义S0与S1的比值P为空隙率，数学关系如式(2)所示。用提取的总长轴、总短轴和有效空隙个数3个参数信息，计算平均长轴、平均短轴等特征参数。平均长轴a、平均短轴b计算如式(3)、(4)所示。

(1)

(2)

(3)

(4)

式中：∑Ai为断面总长轴；∑Bi为断面总短轴；n为断面有效空隙个数。

各断面空隙总面积、空隙总长轴、空隙总短轴、空隙有效个数等信息如表4所示。计算各断面空隙率、平均长轴和平均短轴，如表5所示。

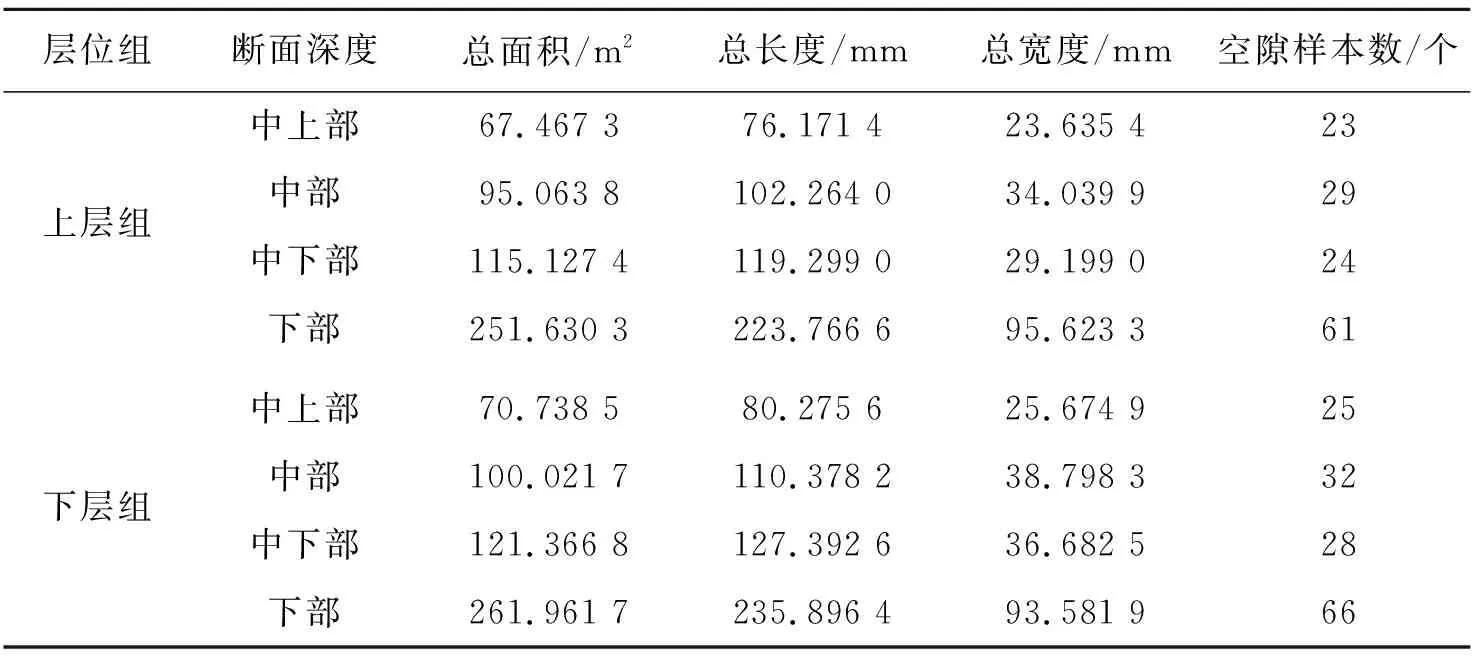
表4 各断面空隙总面积、空隙总长轴、总短轴和空隙有效个数

表5 各断面空隙空隙率、平均长轴、平均短轴

由表4、5可知：上、下层两组数据都表明试件断面总面积不变，空隙面积随试件深度加深，空隙面积越大，空隙率越大。张倩、吴文亮等研究结论是空隙率呈两端大中间小，该文研究选取区域从中上部到下部，空隙率随深度加深而变大，其结论与学者研究结论基本一致。继续处理表5数据，以空隙率为自变量，平均长轴、平均短轴为因变量，进行函数拟合分析，结果如图3所示。

图3 空隙率与平均长度、平均宽度关系图

由图3可知：上、下层两组数据随空隙率增大，平均长轴和平均短轴都呈增大的趋势，平均短轴与空隙率相关系数分别为0.981 7、0.999 7，平均长轴与空隙率相关系数分别为0.707 3、0.745 4，平均短轴增大趋势与空隙率相关系数较高，平均长轴增大趋势与空隙率相关系数较弱，但相关系数都能表明随空隙率增大，平均长轴与平均短轴的增大趋势明显。结合表5中平均长轴、平均短轴在相同空隙率变化下，平均长轴变化程度大于平均短轴变化程度，表明椭圆扁平增大程度大于椭圆类圆增大程度，说明椭圆整体形态上为趋近扁平，表示断面空隙形态随空隙率增大整体空隙狭长程度大于聚集程度，进而说明空隙率越大空隙形态越复杂。

整体空隙呈现狭长形态，可以推断该断面抗劈裂性较低，易发生裂纹的扩展，但该断面空隙空洞聚集较低，可以推断该断面承载荷载能力较强。

经上述研究知：平均长轴、平均短轴可描述断面整体空隙形态几何信息，表征断面空隙整体形态及复杂程度，且能推断断面抗破坏能力，但上述研究不能表征断面空隙结构的复杂性，无法完整表达空隙特性信息，因此需对空隙进一步研究分析。

2 空隙分形特性

2.1 分形理论

分形是用来表征不规则物体的一种手段，根据自相似性原理，用定量的数字直观表现分形体的复杂程度。

根据空隙不规则、零碎特性，采用盒计数方法计算分形维数。以相同尺寸r的网格覆盖图像，得到含有图形像素盒子数N(r)。改变盒子尺寸r，可以得到一系列的盒子数N(r)。将N(r)与r用分形维数D0表示：

N(r)∝r-D0

(5)

两边取对数，得到：

lnN(r)∝-D0lnr

(6)

(7)

式(7)取绝对值即为分形体的分形维数。文中所提分形皆为此节所述分形含义。

2.2 空隙特征提取及分形分析

以像素尺度表示图像空隙坐标，即X、Y轴含义为像素，Z轴含义为灰度值，灰度值范围为0～255，X、Y、Z轴形成空隙灰度值三维图，如图4所示，文中以上层组的4个断面深度空隙灰度值三维图为例进行说明，下层组具有相似规律性。由图4定性分析可知：随断面深度加深空隙三维灰度值三维图越复杂，表明深度越深空隙碎片化、零散化程度越高，整体空隙结构复杂度越高。

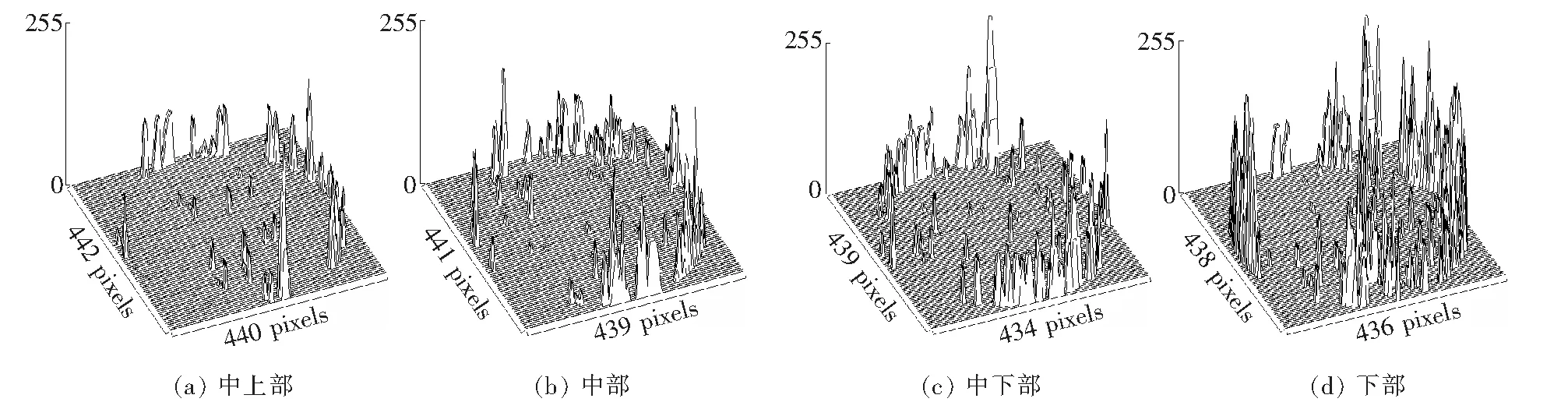
图4 空隙灰度值三维图

分形维数能定量描述分形体复杂度，imagej中调用分形维数算法，求取各断面空隙分形维数拟合图形如图5所示。限于篇幅，图5仅列出上层组4个断面深度分形维数拟合图，根据分形理论知斜率绝对值即为分形体的分形维数，将各断层分形维数和空隙率统计成表6。由图5、表6可知：整体空隙结构越复杂，分形维数越大，表明分形维数能定量表示整体空隙结构的复杂程度。

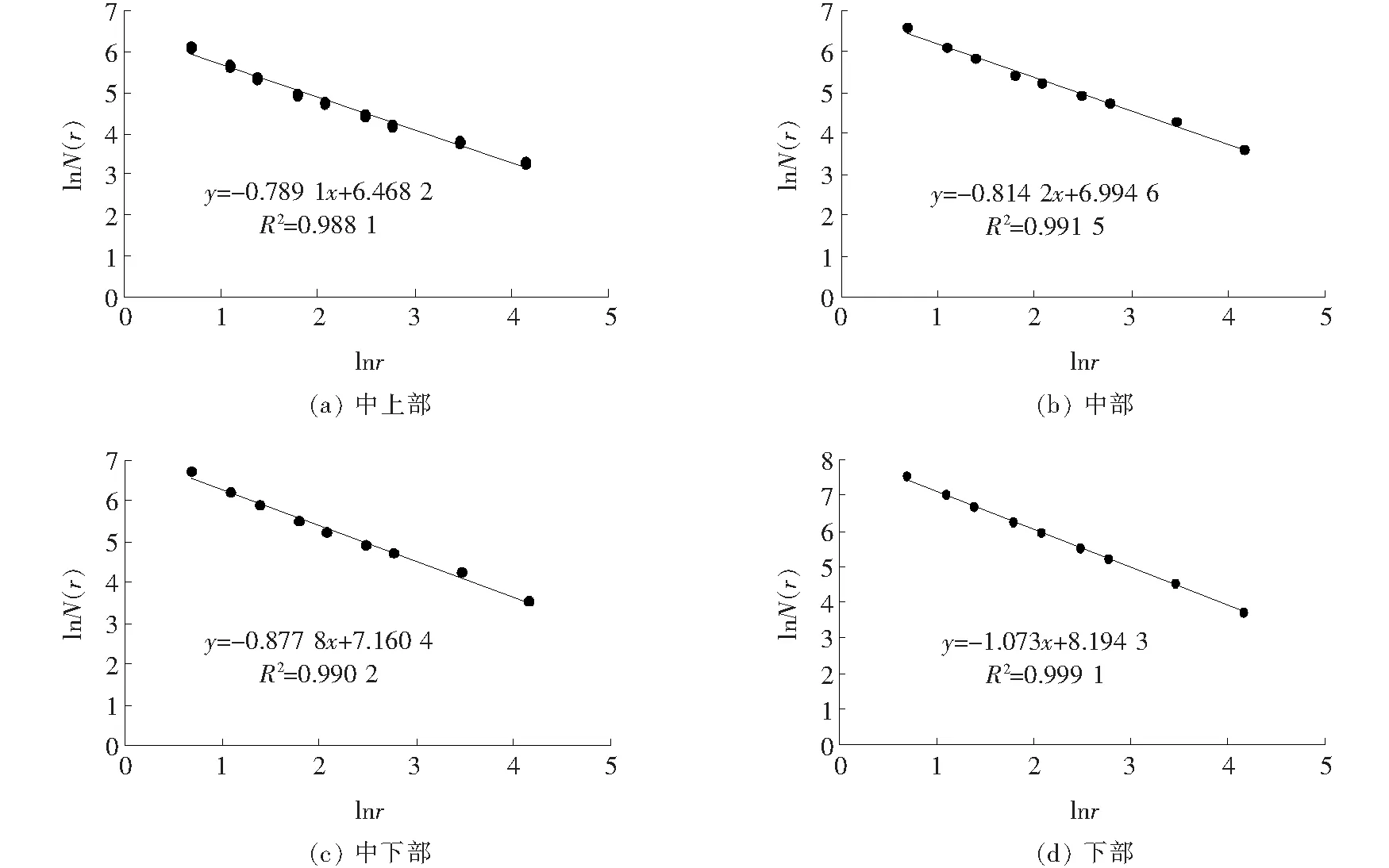
图5 空隙分形维数

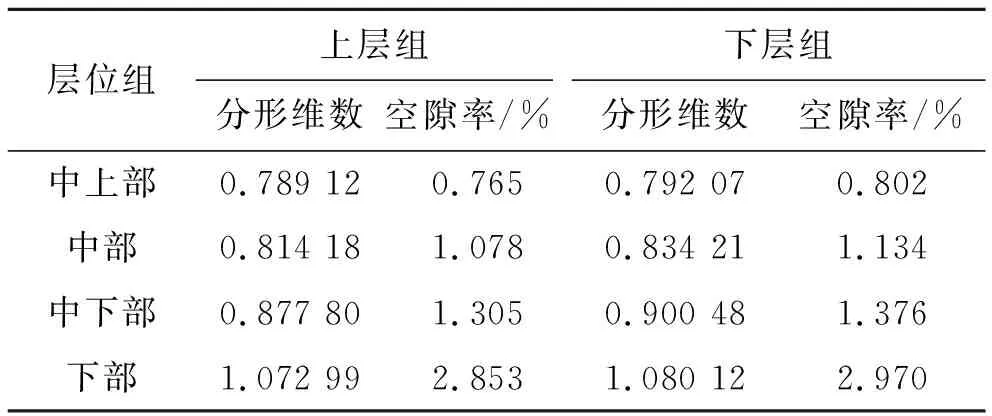
表6 空隙率与分形维数关系

图6 空隙率与分形维数关系图

随断面深度加深空隙分形维数和空隙率都增大，因此将空隙率与分形维数建立联系进行函数拟合分析，函数关系如图6所示。由图6可知：空隙率与分形维数有良好的相关性，上层组、下层组相关系数分别为0.992 8、0.989 3。表明空隙率为0.5%～3.5%时，空隙率越大，空隙分形维数越大，空隙结构越复杂。

由上述研究可知:分形维数以量值直观表征断面空隙的结构复杂程度，它提供了一种定量描述断面整体空隙复杂度的办法，且在一定空隙率范围内，空隙率越大，分形维数越大，空隙结构越复杂。但分形维数只能对断面整体空隙进行表征，会丢失断面局部空隙结构特征信息，无法做到从整体和局部两个层面表征空隙结构信息，因此还需进一步研究。

3 空隙的多重分形特性分析

3.1 多重分形理论

多重分形同样采用盒计数法划分网格，划分时考虑盒子内像素数的差别，将这些差别规一化为概率分布的集，进而用多重分形谱描述空隙局部特征。

用r×r大小的方格覆盖白色空隙，计算每个方格(i,j)中空隙的像素数nij，除以全部空隙总像素∑nij，得到每个方格中空隙占据的概率测度Pij(r)。

(8)

不同盒子尺寸的概率测度P(r)不同，引入奇异性标度指数α，表征每个盒子的奇异程度，表示局部空隙复杂性，每个确定α值下，有相对应的概率测度P(r)组成的子集。概率测度Pij(r)与奇异标度指数α满足如下关系：

P∝rα

(9)

统计具有相同奇异性标度指数α的盒子数目，定义为Nα(r)。类比2.1节分形定义，可得：

Nα∝r-f(α)

(10)

式中：f(α)为相同α值下子集的分形维数，是关于α的多重分形谱。

为计算不规则分形体的多重分形谱，定义一个配分函数χq(r)，对概率测度Pij(r)用q次方进行加权求和，其数学表达式为：

χq(r)≡∑Pij(r)q=rτ(q)

(11)

式中：τ(q)为q阶矩的质量指数，q∈(-∞,+∞)，若q≫1，大概率子集起主要作用，若q≪-1，小概率子集起主要作用。

通过q的加权处理，可对分形集细致研究，经勒让德变换可得：

(12)

由式(12)可知:τ(q)为q的函数，若τ(q)～q函数图像为直线，则α(q)为定值，表明空隙只具有分形特征；若τ(q)～q函数图像为曲线，符合α(q)随q增大而减小，说明空隙具有多重分形特征。

多重分形谱中最大奇异值αmax与最小奇异值αmin之差为谱宽Δα，Δα为概率子集奇异性指数分布范围。概率子集奇异性指数分布越不均匀，多重分形谱f(α)曲线越宽，Δα值越大。该文Δα表征空隙概率测度复杂程度，其值越大，表明空隙局部结构复杂度越高。Δα表达式如下：

(13)

由(13)式知:α取最小值时，P(r)为最大概率子集；α取最大值时，P(r)为最小概率子集。

多重分形谱中最大概率子集维数与最小概率子集维数之差为Δf(多重分形谱中f最小值fmin与f最右端值f右之差)，表示α取最小值时盒子数Nαmin与盒子尺寸r取双对数后的值与α取最大值时盒子数Nαmax与盒子尺寸r取双对数后之差。Δf用来描述多重分形谱的形状，Δf>0表明多重分形谱呈左钩状；Δf<0表明多重分形谱呈右钩状，Δf=0表明多重分形谱呈钟状。Δf表达式如下：

(14)

q=0时，P(r)测度具有相同的贡献率，此时多重分形谱中f(α)取最大值，根据式(5)、(10)知fmax与分形维数D0相等，都表征断面整体空隙结构的复杂性。

由上可知，多重分形中谱参数fmax表征断面中整体空隙结构的复杂性，谱参数Δα表征断面中局部空隙结构复杂性，谱参数Δf描述多重分形谱的形状，通过3个参数从整体空隙结构和局部空隙结构两个不同层面来刻画空隙结构。

3.2 各断面空隙多重分形谱及谱参数分析

获取断层图像空隙的α(q)～q函数关系图，如图7所示，因各断层图像的α(q)～q函数关系类似，都符合α(q)随q增大而减小这一特征，且图像所占篇幅较大，图7只列出了上层组中上部处的α(q)～q函数关系图。由图7可知:α(q)随q增大而减小，结合式(12)，可知各断层图像空隙都具有多重分形特征。

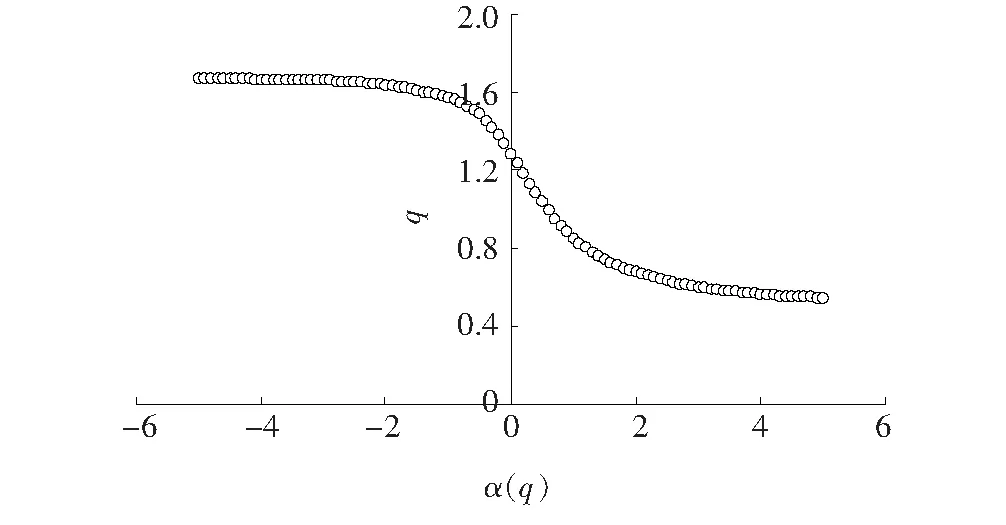
图7 α(q)～q函数关系图

调用多重分形模块算法获取断层图像空隙多重分形谱[f(α)～α图]，如图8所示，因上、下层两组规律相似，此处以上层组进行说明。对图8进行谱形分析可知，断层中上部与中部多重分形谱曲线形状类似，断层中下部与下部多重分形谱曲线形状接近。提取各断层多重分形谱谱参数fmin、f右、Δf、αmin、αmax、Δα及fmax等数据及空隙率,构成表7。

图8 多重分形谱

表7 谱参数

由表7可知，中上部、中部的Δf明显小于断层中下部、下部的Δf，且各断层Δf都小于0，反映在多重分形谱上断层中上部、中部多重分析谱明显呈右钩状，中下部、下部多重分形谱呈略右钩状即更趋近于钟状，略右钩状多重分形谱比右钩状多重分形谱的奇异性指数α变化范围要大，即αmax与αmin的差值Δα越大。Δα越大局部空隙奇异性越高，凸起与凹陷程度、碎片化程度和锐化程度越高，局部空隙结构越复杂。结合图4可知:断面深度越深，细小空隙越多，空隙越零碎，空隙锐化程度越高，空隙局部结构越复杂，可知Δα正好能够表征局部空隙碎片化、锐化程度。表7中上、下层两组fmax值随深度加深而越大，表明深度加深整体空隙结构越复杂，这与分形维数D0表征整体空隙结构复杂度一致，说明fmax和D0都能定量刻画整体空隙结构的复杂度。

将各断面空隙率与谱参数Δα、Δf和fmax进行函数拟合分析，函数关系如图9所示。

图9 各断面空隙率与谱参数函数相关性

由图9可知:空隙率与Δα、fmax相关性良好，与Δf相关性较差，但随空隙率增大，Δα、fmax和Δf都有增大趋势。表明空隙率为0.5%～3.5%时，空隙率越大，空隙结构局部复杂度与整体复杂度越高。

fmax与D0都表征断面整体空隙结构复杂，但同一断面空隙fmax与D0值不等。其原因是求D0时不同尺寸r下的像素是对所有r×r大小区域的像素作平均，所得到的分形维数是对空隙整体上的平均描述；求取fmax时，根据网格中实际像素计算各区域的概率，统计所有概率的差别，然后加权处理后分成多个α子集研究，误差较小，准确性更高。

空隙结构越复杂，空隙凹陷与凸起、锐化和碎片化程度越高，雨水对这些空隙结构易腐蚀，进而破坏路面，狭长空隙易形成空隙之间的贯通，破坏路面结构，路面不易养护，因此研究空隙结构复杂度对路面雨水渗流和水损害有一定意义，结合工程抗滑性能指标，可提高路面使用性能。

多重分形不仅能从整体空隙与局部空隙两个层面分析空隙结构的复杂性，且fmax在描述整体空隙时比分形维数D0更准确。因此将多重分形运用在空隙研究上，能够更加准确获取更丰富的空隙结构信息，且能够推断雨水对路面损害情况，对路面养护具有一定指导意义。