刃脚入土极限阻力系数Nγ及地基土破坏形态研究

李宇航

(中铁十八局集团第五工程有限公司， 天津市 300222)

大跨桥梁墩台水中基坑施工时，双壁钢围堰常作为施工围护结构广泛应用。在结构设计与下沉稳定性验算时，为保证钢围堰结构的安全可控下沉，需估算刃脚极限阻力。当底部土体未掏空时，刃脚极限阻力可归结为刃脚底部土体极限承载力问题。借鉴浅基础承载力的计算思路，可采用滑移线、极限平衡和极限分析等方法求解。针对刃脚下沉承载力问题亦有部分研究报道。

Solov′ev基于极限平衡理论与有限差分法，计算沉井楔形刃脚在砂土和黏土中的承载力，说明刃脚形态和斜面角度对承载能力影响显著；Chakraborty采用极限分析有限元法计算楔形基础承载力系数，列出了多参数影响下的曲线图；徐伟等采用有限差分法和滑移线场理论探讨了环形刃脚踏面和斜面承载力规律；闫富有等建立圆形沉井刃脚土体近似滑移线场，讨论了刃脚形状和切土深度对承载力的影响；周和祥等利用柱孔扩张理论，提出刃脚极限阻力的理论解答，分析了切土深度及剪胀效应对刃脚土阻力的影响。

综上可知，刃脚承载力问题归于楔形浅基础范畴，已有不少研究成果。然而，现阶段岩土承载力课题分析方法，特别结合分析土体破坏形态问题，仍有必要开展进一步的研究。

该文针对刃脚极限阻力问题，应用刚体平动运动单元上限有限元(UBFEM-RTME)开展系列分析。考虑刃脚角度、刃脚与地基接触粗糙程度及土体参数等综合因素，研究由土体自重引起的刃脚入土极限阻力系数上限解和地基极限状态网状滑移线破坏形态规律，为双壁钢围堰设计施工提供一定理论借鉴。

1 问题描述与假设条件

矩形钢围堰长宽尺寸远大于其厚度，因此，可将刃脚入土极限阻力问题简化为沿着短边的二维平面应变问题考虑，如此处理不失一般性。刃脚入土极限阻力计算模型如图1所示。

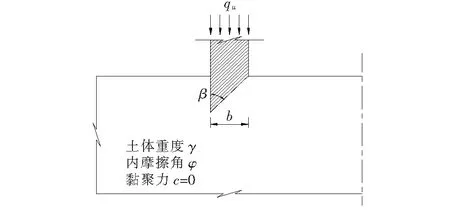
图1 刃脚入土极限阻力计算模型示意图

具体假设条件如下：

(1) 由钢围堰沿短边横向的对称性，取对称轴左半部分加以考虑，且认为入土下沉时不发生偏斜，即刃脚只发生竖向位移而不发生水平位移或旋转。

(2) 刃脚入土时的土体表面为水平自由面，且处于刃脚斜面上端；刃脚在计算模型中予以考虑，但设定为自重为零的刚性体。

(3) 刃脚斜面角度为β，踏面宽度为b，模型左右及下部范围选取远大于踏面宽度b。

(4) 地基假定为均质各向同性砂土，且服从相关联流动法则的摩尔-库仑材料，重度为γ，内摩擦角为φ，黏结力c为0。

(5) 刃脚侧面、斜面与地基土接触面摩擦角为α；考虑接触面完全光滑(α=0°)和接触面完全粗糙(α=φ)两种情况。

(6) 刃脚入土极限状态时，对应极限荷载为均布力qu=0.5γbNγ。

为分析极限荷载qu的多参数影响规律，应用土体自重作用代表的极限阻力系数Nγ作为系列无量纲解，求解方法见下节。其中刃脚斜面角度β取45°、60°、75°和90°共4种情况；土体内摩擦角φ按2.5°的间隔在15°～40°内取值。

2 有限元模型建立

刃脚入土极限阻力系数Nγ上限有限元计算模型如图2所示。图中显示位置坐标系建立，x和y轴正方向分别向右和向上，速度坐标系与此一致。模型到底部边界延伸距离为L1，刃脚到模型左右边界距离为L2，建模时L1、L2应取足够大值以消除边界效应。以β=45°为例，图2显示了上限有限元网格，此网格为UBFEM-RTME计算模型初始网格，计算过程中仍需实施多次网格更新。

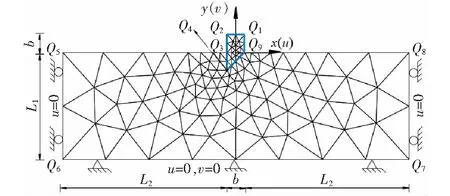
图2 刃脚入土极限阻力系数计算模型(以β=45°为例)

刃脚(自重为零的刚性体)范围内单元竖向速度值v均设置为-1，水平速度值u设置为0。砂土黏结力c=0，则间断线耗散能值为0。依上限定理，列虚功率平衡方程如式(1)，代入qu=0.5γbNγ即可获得目标函数(极限阻力系数Nγ)如式(2)：

(1)

(2)

式中：ne为单元总数；Ai与vi分别为第i个单元的面积与竖向速度。

地表边界为水平自由面，模型其余边界施加如图2所示速度约束。除速度边界约束外，还需施加几何约束以保证各边界上的节点均沿各自边界移动。

3 刃脚入土极限阻力系数Nγ上限解

3.1 Nγ计算结果对比(β=90°)

当β=90°时，刃脚入土极限阻力确定问题与条形基础承载力问题一致。考虑刃脚与地基土接触面完全粗糙且荷载仅与土体自重相关，此时极限阻力系数Nγ既有研究结果颇丰。如Chen、Michalowski、Soubra、Zhu、Yang和杨峰等均应用不同破坏机构刚性滑块上限法对Nγ进行求解。而Martin则采用滑移线法，同时从应力场和速度场两方面建立高密度滑移线网格，由此得到的Nγ数值解可认定为精确解。

应用刚体平动运动单元上限有限元计算得到的接触面完全粗糙条件下极限阻力系数Nγ与已有文献对比如表1所示。当φ=20°时，该文结果较之杨峰上限解小23.8%，比Chen等上限解小49.5%，比Michalowski等上限解小33.6%，比Soubra等上限解小11.54%，比Zhu等上限解小33.9%，比Yang等上限解小36.4%。对于承载力问题，通常上限解越小计算结果越好，说明该文上限解更优。

对比其他数据均发现，在上限理论框架内，该文Nγ计算结果小于Chen、Michalowski、Soubra、Zhu、Yang和杨峰等上限解，且与Martin高密度滑移线数值解接近，由此验证了计算手段和结果的可靠性，可用来计算分析更普遍条件下的刃脚入土极限阻力系数Nγ。

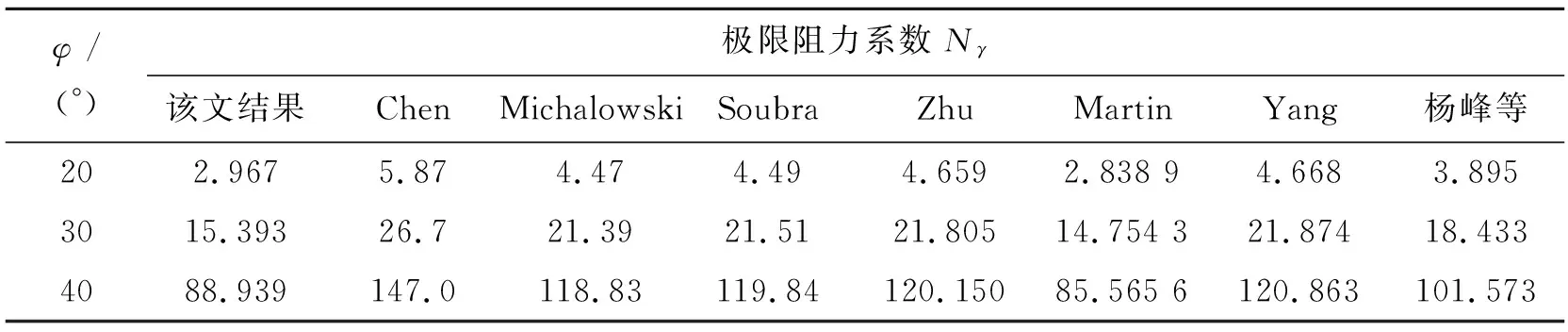
表1 极限阻力系数Nγ计算结果对比(β=90°, α=φ)

3.2 刃脚入土极限阻力系数Nγ规律分析

利用刚体平动运动单元上限有限元程序对双壁钢围堰刃脚入土极限阻力开展计算分析，获得88组正交参数对应的极限阻力系数Nγ结果见表2，进一步绘制Nγ与φ关系曲线见图3。

表2 刃脚入土极限阻力系数Nγ上限解

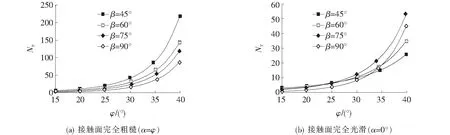
图3 刃脚入土极限阻力系数Nγ与土体内摩擦角φ关系曲线

图3(a)为刃脚与地基土体接触面完全粗糙时的极限阻力系数Nγ上限解曲线。由图3(a)看出：Nγ随土体内摩擦角φ增大而增大，表明较大φ值对应的刃脚入土阻力也较大。同时，随着刃脚斜面角度β增大，Nγ值逐渐减小，表明刃脚较“钝”时更容易破土，这与接触面完全粗糙时，较“钝”刃脚破土面积越小有关。特别地，当φ越大时，Nγ随β增长而减小得越明显。例如φ=40°，β=90°对应的Nγ值比β=45°时的Nγ值减小了约60%。

图3(b)为刃脚与地基土体接触面完全光滑时的极限阻力系数Nγ上限解曲线。由图3(b)可知：①Nγ随φ增大而增大；当β=45°～90°时，φ从15°～40°变化，Nγ值分别增大了5.74倍、9.86倍、18.2倍、37.8倍，表明随着φ增大，Nγ增大更为明显；② 刃脚斜面角度β增大时，Nγ值相应增大，即刃脚越“钝”越难破土，这与接触面完全光滑条件下，刃脚下方土体仅为单侧破坏相关；不过，β=90°时，受地表边界影响，该规律与内摩擦角φ的综合影响变得复杂。

对比图3(a)和(b)，刃脚与土体接触面粗糙时Nγ值较之光滑时大许多，且与刃脚斜面角度β的影响规律相反。原因可能在于双壁钢围堰仅假定竖直下沉，当光滑接触面条件时，刃脚外侧(垂直侧)土体不再受到挤压，且下方破坏范围也显著减小所致。这在后续破坏模式讨论中进一步体现。同时也说明，刃脚与地基土体的摩擦力也是影响下沉阻力的关键因素之一。

4 刃脚入土极限状态土体破坏模式

利用UBFEM-RTME程序计算双壁钢围堰刃脚入土极限阻力系数Nγ的同时，可得到近似网状滑移线(由有效速度间断线构成)破坏模式，这有利于揭示刃脚处地基土破坏机理。

4.1 地基土破坏模式(β=90°)

当β=90°时，如3.1节所述，刃脚入土极限阻力确定与条形基础承载力问题一致。绘制β=90°，φ=30°，α=φ和α=0°该文获得的地基破坏模式如图4所示。对比图4(a)、(b)可知：① 采用UBFEM-RTME方法及程序搜索获得的以有效速度间断线网表征的地基破坏形态，与Martin建立的高密度滑移线网格形态十分近似，数值解仅相差4.1%；② 刃脚与地基土接触面摩擦角α对破坏模式影响显著，该文与Martin网格破坏形态近似。

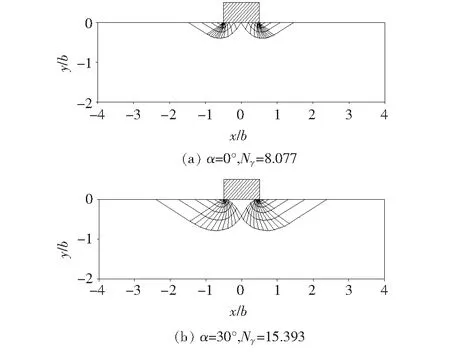
图4 地基土破坏模式(β=90°, φ=30°)

4.2 刃脚斜面角度β对破坏模式的影响

图5为接触面完全粗糙时，β=45°～75°，φ=25°对应的刃脚处地基土破坏模式。此时，刃脚两侧均发生破坏，且β值越大，即刃脚较“钝”时，下部和两侧的破坏范围反而越小，反映出Nγ值随之减小的主要原因。还可发现，β值较大时，紧贴刃脚斜面出现了刚性的弹性核，刃脚两侧破坏形态更为近似，这些与现有文献关于条形基础地基破坏模式的主要形态特征逼近，进一步印证该文结果的可靠性。

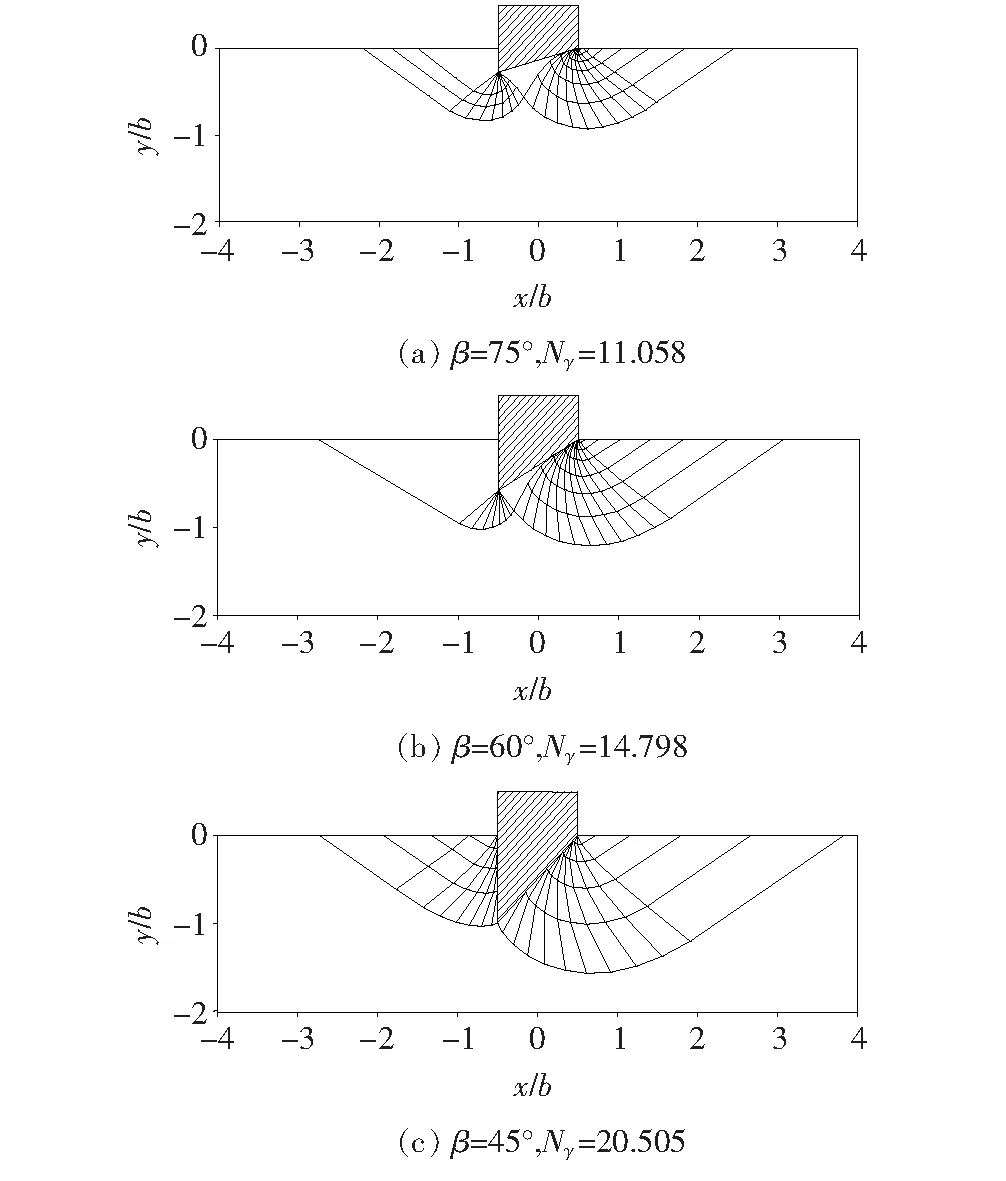
图5 不同刃脚斜面角度β对应的地基土破坏模式(φ=25°,α=25°)

4.3 刃脚与地基土接触面特性对破坏模式的影响

图6为β=45°，φ=20°时，刃脚与地基土接触面分别为完全光滑(α=0°)和完全粗糙(α=φ)条件下对应的刃脚处地基土破坏模式。

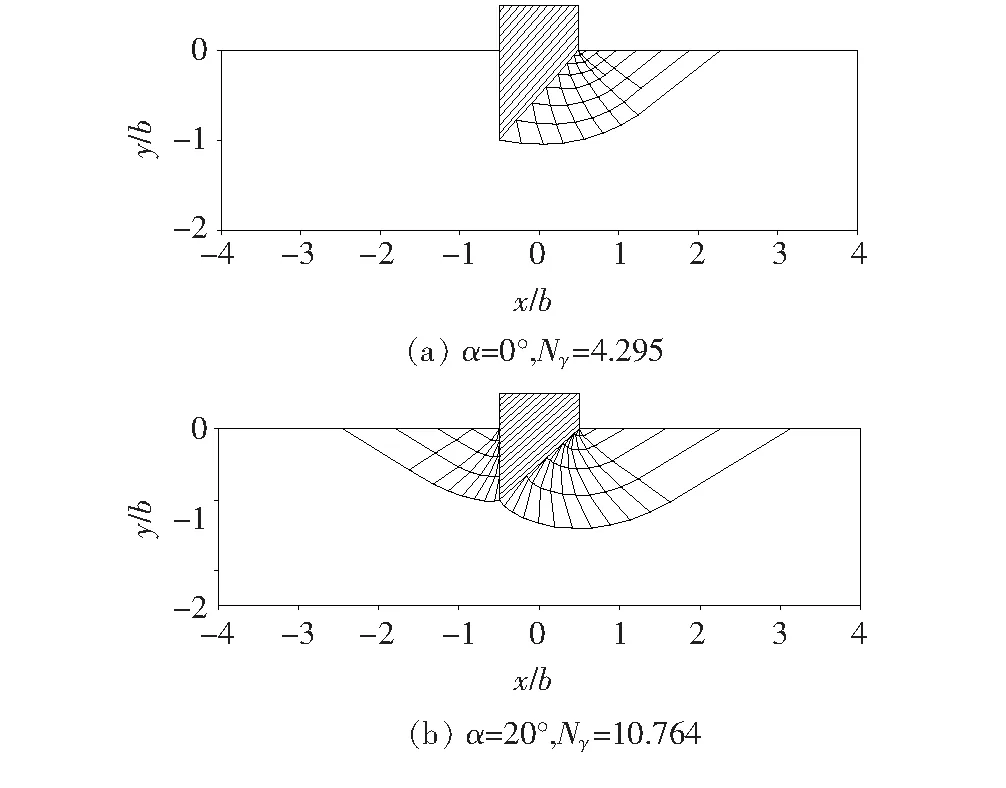
图6 刃脚与地基土接触面特性对应地基土破坏模式(β=45°,φ=20°)

由图6可看出：接触面完全光滑时地基土破坏模式只含有扇形破坏区与被动区，且刃脚斜面单侧破坏，破坏范围较小；而接触面完全粗糙时，刃脚斜面一侧网状滑移状破坏范围向下加深，范围较大，而且由于外侧接触面的摩擦作用，外侧也出现了范围不小的破坏区域，这也是其极限阻力系数Nγ较之光滑接触面条件下对应值显著增大的原因。通常，刃脚与地基土接触面摩擦作用受土体性质、施工工艺等多种因素影响，摩擦角α应合理地加以考虑。

4.4 土体内摩擦角φ对地基破坏影响

图7(a)为β=60°，φ=20°时，刃脚与地基土接触面完全光滑(α=0°)条件下地基土破坏模式，其反映了刃脚斜面单侧滑移线网破坏特征。将相同条件下，内摩擦角φ取15°～40°对应的外侧主要滑动面叠加绘制如图7(b)所示。由图7(b)可看出：当φ值增加，刃脚斜面单侧破坏范围随之增加，由此引起极限阻力系数Nγ显著增大。尽管限于篇幅未绘图展示，刃脚与地基土接触面完全粗糙(α=φ)时也具有类似规律，且刃脚外侧出现的破坏区域范围一并增大。

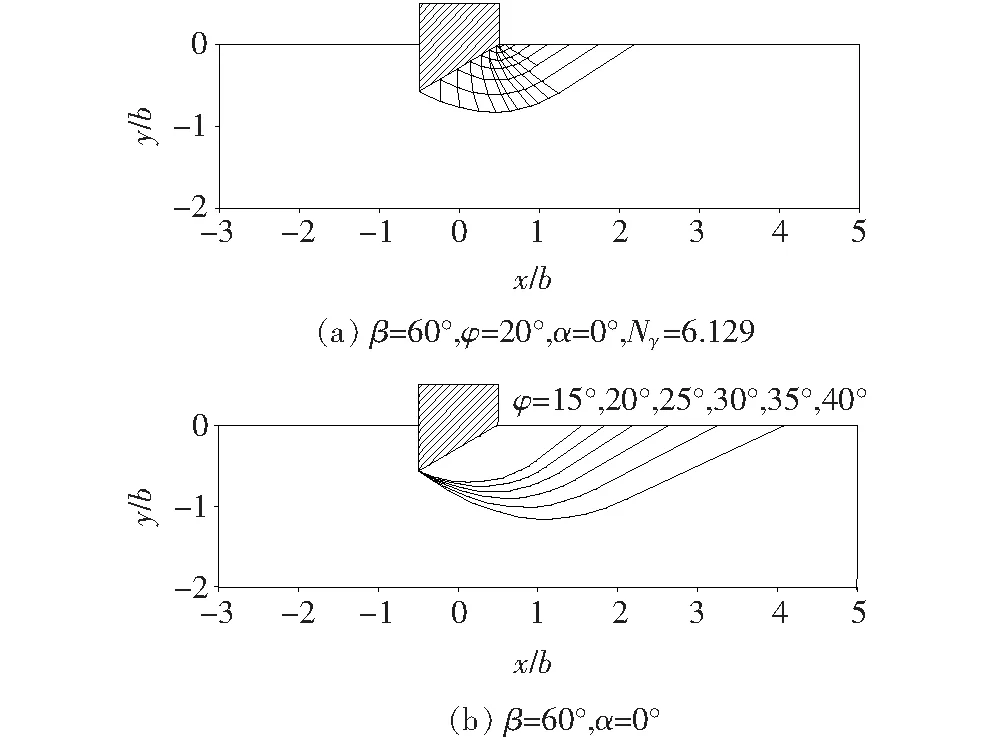
图7 不同土体内摩擦角φ对应地基土破坏模式

5 结论

(1) 刃脚入土极限阻力系数Nγ上限解与接触面摩擦角α显著关联。α较小时，不仅刃脚斜面侧破坏范围小，且刃脚外侧基本不发生破坏；而α较大时破坏范围加大，且刃脚外侧亦发生破坏。

(2) 接触面的摩擦效应直接解释了刃脚“钝”“锐”与入土难易程度的反向规律。一方面设计施工时应合理选取刃脚斜面角度β；另一方面，刃脚与地基土接触面摩擦效应与施工工艺相关，摩擦角α取值应审慎考量，且关联到β值的确定。

(3) 各种条件下地基土内摩擦角φ对极限阻力系数Nγ的影响均较大，体现出较大的φ值，引发了较大破坏范围，抵抗破坏的效应随之增加。

(4) 尽管考虑了刃脚斜面角度β、土体内摩擦角φ和接触面摩擦角α等综合影响，实际工程中的其他多种因素并未计及，相关工作有待进一步深入。