具有局部性质的球面插值样条曲线的构造

王 倩，潘 乐，张洁琳，彭兴璇

具有局部性质的球面插值样条曲线的构造

王 倩1，潘 乐1，张洁琳2，彭兴璇1

(1. 辽宁师范大学数学学院，辽宁 大连 116021；2. 吉林大学数学学院，吉林 长春 130023)

高维球面样条曲线拟合技术在计算机动画和惯性导航等领域都受到广泛地关注。实际中常需球面曲线插值给定的数据点，并要求曲线具有一定的连续性和良好的局部性质。此前的方法存在一定的局限性。为此，基于球面Bézier曲线，提出了一种仅利用插值点位置信息便可在任意维空间中构造2球面插值样条曲线的新方法。首先，通过映射拟合出了插值点处的高阶导矢，然后给出了曲线段在端点处2Hermite插值的充要条件，即控制顶点的解析计算方法，最后构造出2连续的球面Bézier插值样条曲线。该方法属于局部构造方法，样条曲线上个别插值点的扰动不会对全局产生影响；样条曲线具有显式表达式，无需通过非线性方程组求解控制点坐标。数值实验表明，该方法适用范围广，局部性质好，灵活度高。

球面样条；球面Bézier曲线；插值；参数连续；刚体运动

随着现代科技及计算机领域的飞速发展，球面样条曲线在很多领域都引起了广泛地关注。研究球面样条曲线的构造对计算机动画、计算机辅助几何设计和惯性导航等领域都有重要的理论和实际意义。例如，在惯性导航和计算机动画中，刚体运动的生成是一个基本问题。刚体的旋转运动可用三维球面曲线(或单位四元数曲线)来表示。与其他方法相比，单位四元数具有4个变量和3个自由度，因此在描述旋转运动时更具优势。本文围绕如何构造一段光滑的球面样条曲线进行讨论。

欧氏空间中存在着几种经典的样条曲线的构造方法[1]，如Bézier曲线、B样条曲线以及NURBS曲线等。由于球面的非欧性，无法直接利用上述几种方法来构造球面样条曲线，但以这些方法为基础，研究人员们建立了多种构造球面插值样条曲线的方法[1-12]，并且各有优势。下面介绍与本文相关度最高的2种构造方法。

方法2.直接构造法[12-20]。Shoemake[9]将欧氏空间中的DE CASTELJAU算法[3]向低维单位球面进行了推广，并给出了2条球面Bézier曲线1光滑拼接的条件。KLETTE等[10]将上述算法推广到了维单位球面上，并构造出了1球面Bézier样条曲线。进一步地，以文献[8-11]为基础，文献[2]对任意维球面Bézier曲线在端点处的性质进行了研究，并利用共轭导矢的概念构造出2球面Bézier样条。但是该方法无法对曲线形状进行局部控制。Luo等[12]在此基础上，对该方法进行改进优化，使得曲线的速度和加速度波动更小，同时放松了对给定条件的限制，解决了任意插值问题解的存在性问题。但该方法还存在一些局限性，不仅需要提前给出若干个插值点的位置信息，还需要给出插值点处的导矢信息，由于球面具有非欧结构，在给定导矢信息时还需考虑是否满足相应的条件。

为了解决上述研究存在的问题，本文提出了一种新的球面样条曲线的构造方法。该方法适用于任意维空间，属于局部构造法，只需相邻2个插值点的位置信息即可构造出满足条件的样条曲线，因此在个别点发生扰动时，也不会对全局产生影响，这样就放松了对条件的限制，使得算法适用范围更广，同时更加高效。

1 预备知识

Popiel和Noakes[2]将DE CASTELJAU算法[3]进行了推广，给出球面Bézier曲线的递推定义。其定义为：

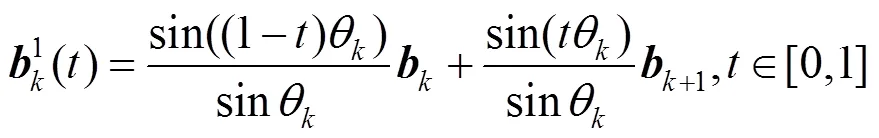
对于=2,3,···,,=0,1,···,-1，令

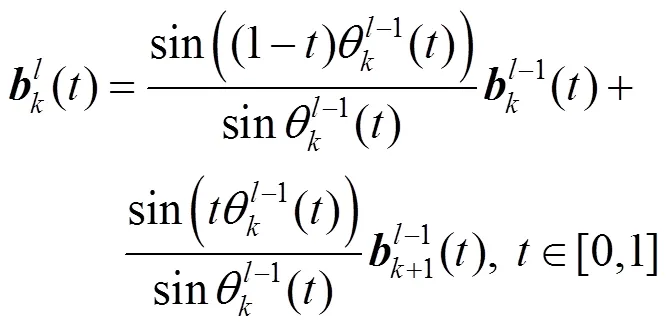
其中

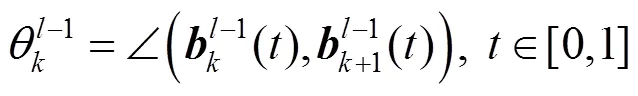
需要注意的是，本文和等符号的上标均表示递推级数，而不表示次幂。

根据上述定义，Popiel和Noakes[2]给出了一次球面Bézier曲线一些基本性质。

引理1. 对于=0,1,···,-1,Î[0,1]，有

另外，Popiel和Noakes[2]还给出了次球面Bézier曲线在端点处的一些性质。

2 球面样条曲线的构造

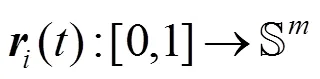
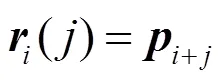
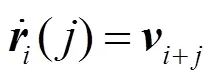
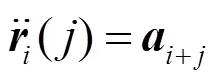
其中，=0,1。

由引理2性质(1)和(2)可知，球面Bézier曲线具有端点插值性，所以()可用一条五次的球面Bézier曲线段来表示，假定其控制顶点为(= 0,1,···,5)。

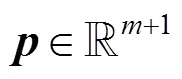
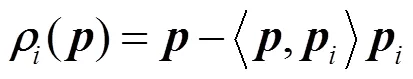
(2)是线性的；

(3) 若是一条连续曲线，则是一个连续映射。

2.1 C0连续

本小节将考虑如何选取()的首末控制顶点，使其插值点和+1。

定理1. 令=1,2,···,，则五次球面Bézier曲线()在端点处满足式(4)的充分必要条件为

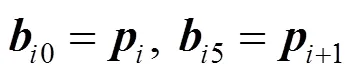
证明：由球面Bézier曲线的端点插值性即可证明该定理。

2.2 C1连续

本文将考虑如何选取()的中间控制顶点，使其在端点处满足式(5)。

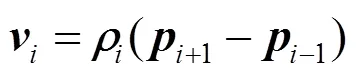
在给出曲线()的2个控制顶点1和4的计算式之前，先介绍与和+1有关的引理。

引理3. 对于=1,2,···,，令

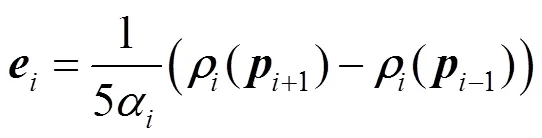
证明：由的定义式可知

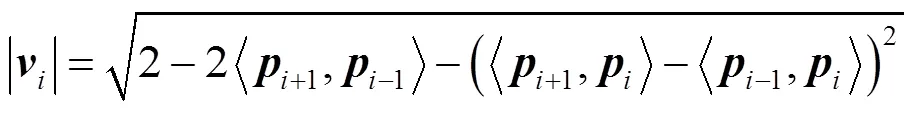
再由的性质(2)可知，即为单位化的。

在上述工作的基础上，可以给出五次球面Bézier曲线()控制顶点1和4的计算式。

定理2. 令=1,2,···,，则五次球面Bézier曲线()在端点处满足式(4)和式(5)的充分必要条件是式(8)，以及

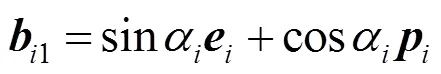
和

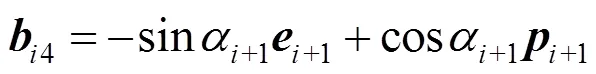
成立。

证明：首先证明必要性，已知有式(8)，式(12)和式(13)成立，直接计算即可证得()在端点处满足式(5)。

接着证明充分性，根据定理1可知球面Bézier曲线()在端点处满足0连续当且仅当式(8)成立。进一步地，由引理2条件(3)和引理1条件(1)可知

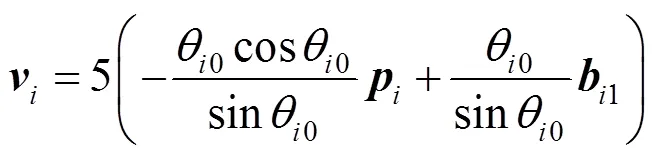
将式(9)代入式(14)可得

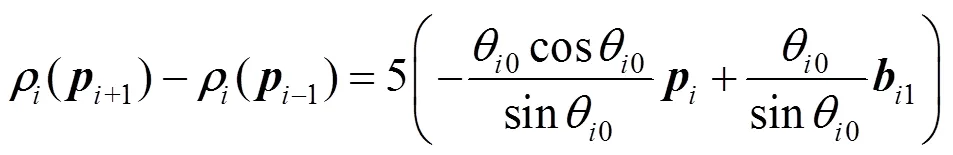
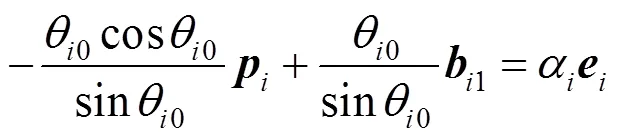
由此可以得到式(12)。

类似地，式(13)也成立，进而定理得以证明。

进一步地，借助引理3，式(13)还可以表示为

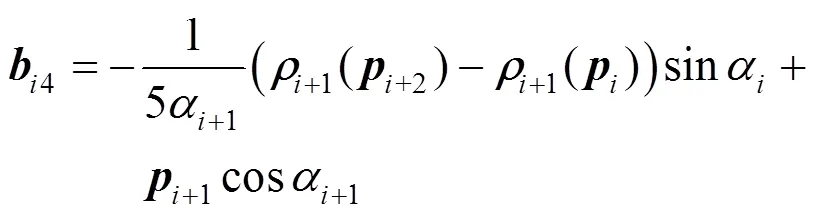
2.3 C2连续

根据参数连续性的定义可知，若曲线段在连接点处一阶和二阶导矢均相等，则在该点处是2连续的。本文利用该定义对曲线()的2Hermite插值问题进行了研究。

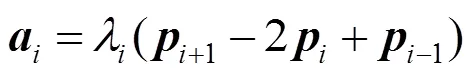
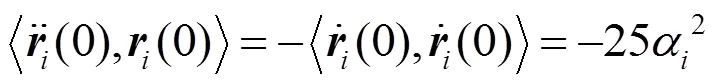
因此需要引入系数，并通过式(19)来拟合出球面曲线()在点处的二阶导矢。

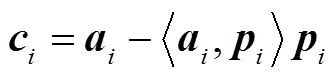
为了简化表达，令

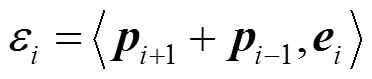
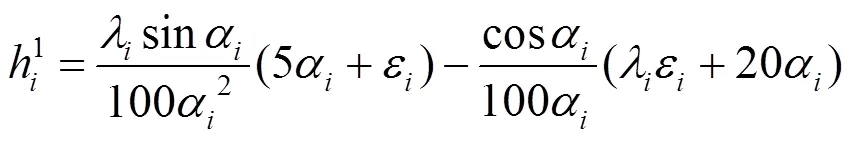
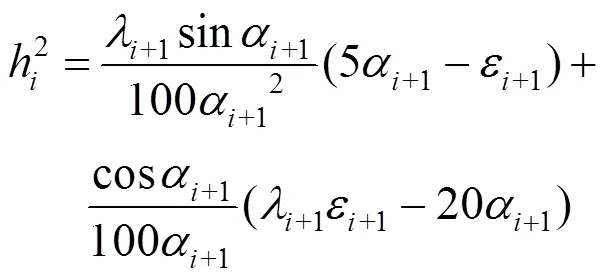
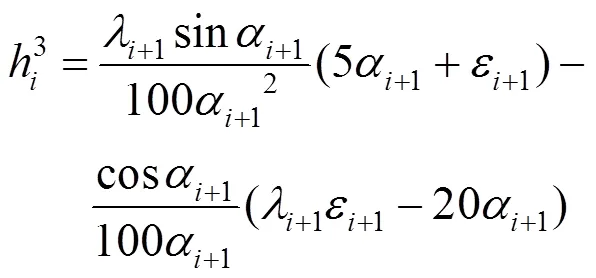
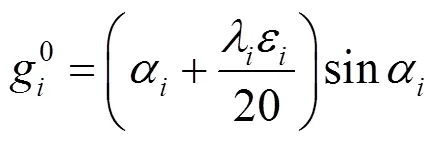
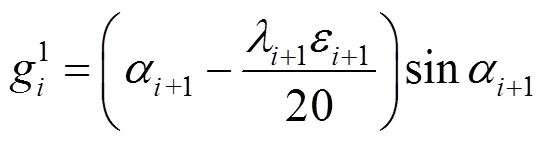
在上述工作的基础上，可以给出五次球面Bézier曲线()控制顶点2和3的计算式。

定理3 令=,1,2,···,，则五次球面Bézier曲线()在端点处满足式(4)~(6)的充分必要条件是：表达式(8)，(12)和(13)，以及

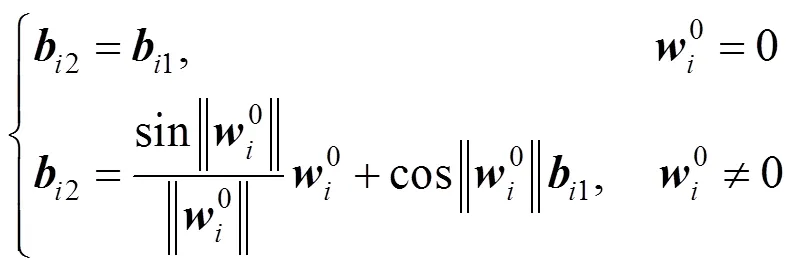
和

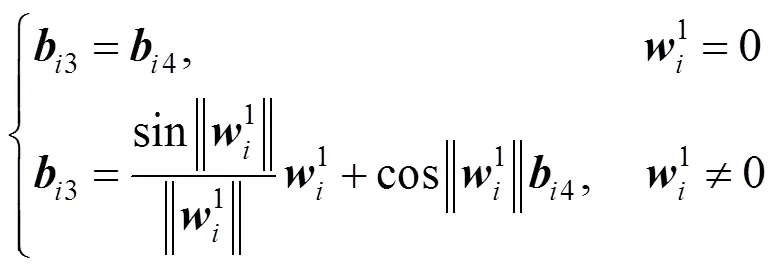
成立，其中

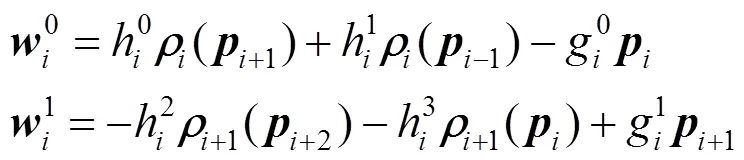
证明：首先对必要性进行证明，已知2和2的显式表达式(28)和式(29)，显然可证得()在端点处满足式(6)。

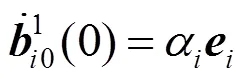
用向量1与式(20)的两端同时作内积，得到

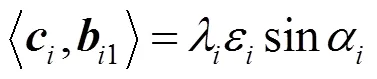
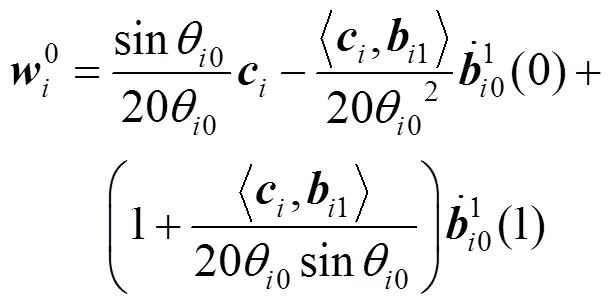
将式(31)~(33)代入式(34)中，可得

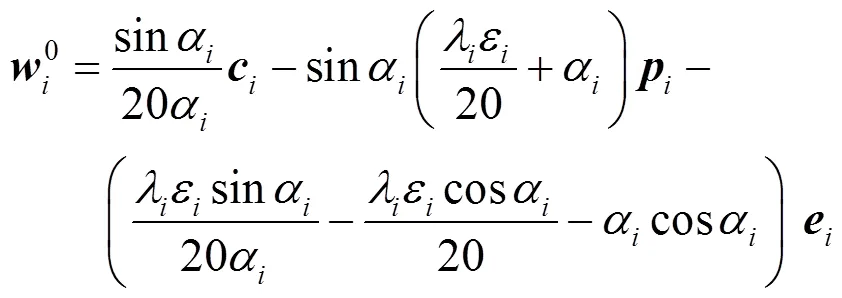
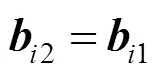
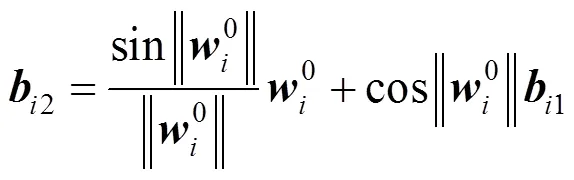
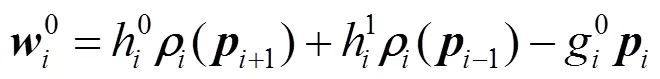
类似地，式(29)也可证得。

利用上述结果，即可构造出2连续的球面插值样条曲线。

3 实 验

通过实例证明本文方法的优势。

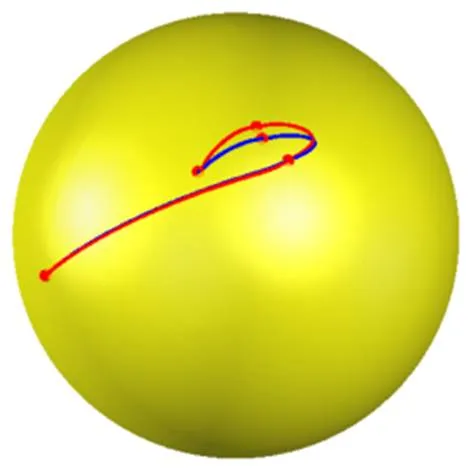
图1 基于原始数据的球面插值样条曲线(蓝色曲线)和扰动数据的球面插值样条曲线(红色曲线)

需注意的是，基于四元数的球面样条曲线构造方法[4,7-8]是无法应用到二维球面上的。

本文方法也可应用到高维球面上，例如刚体旋转运动的插值，即单位四元数样条曲线的插值。

例2.给定刚体旋转运动的插值数据(表1)，借助四元数的相关知识[4,8-9]可分别求出其对应的四元数组，即

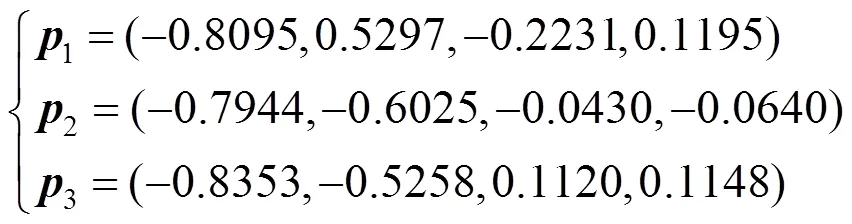
利用本文方法，可以得到2连续的单位四元数插值样条曲线，进而得到相应的光滑的刚体旋转运动。图2是刚体中心点旋转运动轨迹，此时，刚体的中心点与世界坐标系原点不重合(在三维欧氏空间中安装一个正交标架，称为世界坐标系，在刚体上安装一个正交标架，称为移动坐标系，则刚体运动可以视为世界坐标系与移动坐标系之间的坐标变换[21])。在此基础上，假定刚体的平移运动为直线运动，就可得到以图3所示曲线为方向曲线的光滑的刚体运动。图3是该运动的等时间离散化表示，其中渐变黄色立方体表示运动的插值位置。

表1 刚体旋转运动插值数据

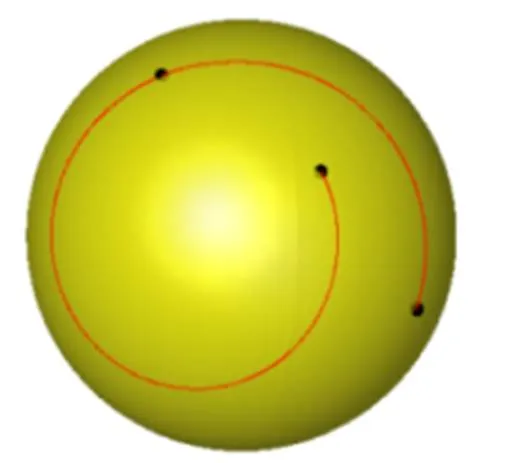
图2 刚体中心点旋转运动轨迹

图3 刚体运动示意图

例3.给定5个时刻刚体旋转运动的插值数据以及扰动数据。与例2类似， 假定刚体的平移运动为直线运动，分别利用本文方法和文献[2]方法，可以得到相应的插值给定数据的光滑的刚体运动，如图4和图5所示。从图4中可以看出，本文方法在扰动首末时刻数据时只对首末段刚体运动造成影响，扰动中间时刻数据时只会对与该时刻相关的2段运动造成影响。从图5可以看出，文献[2]方法在扰动某个时刻的数据时，其后的运动都会发生变化。由此验证了本文方法具有局部性质，通过局部调整旋转角和旋转轴的数据就可以灵活地控制刚体在相应时刻下的旋转运动姿态。

实际上，例3中的刚体平移运动的轨迹可以改为任意曲线。

例4. 给定3个时刻刚体运动的插值数据，见表2，假设刚体的平移运动轨迹为正弦曲线，类似地，可得到插值给定数据的刚体运动，如图6所示。

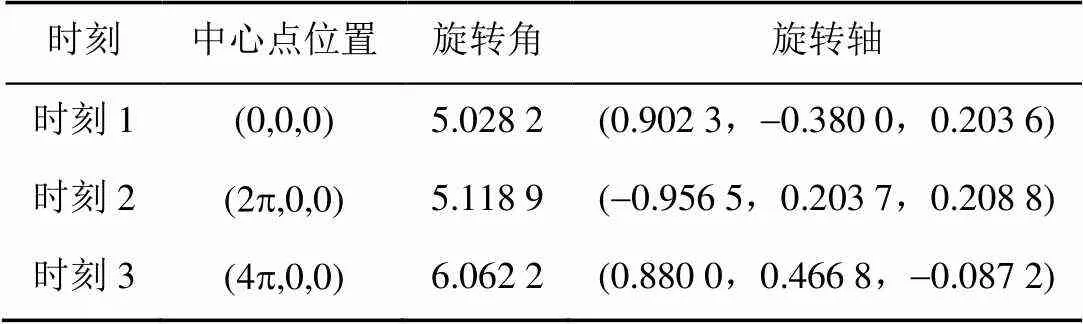
表2 刚体运动插值数据

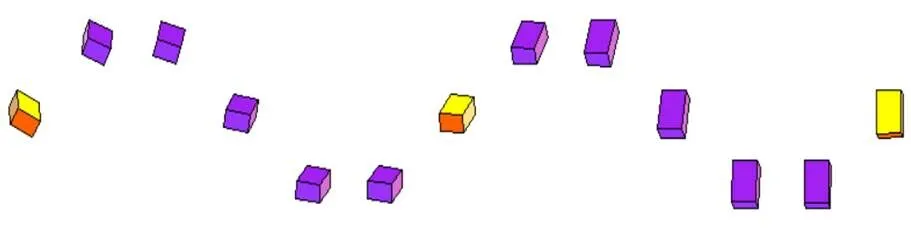
图6 平移轨迹为正弦曲线的刚体运动示意图

4 结 论

在插值点位置信息不变的前提下，本文方法存在对曲线的形状缺乏灵活控制的问题。实际上，在拟合插值点处的导矢信息时，可以通过改变一阶及二阶导矢的长度，即引入额外的参数来解决上述问题。所以在以后的研究中，将会考虑如何构造几何连续的球面样条曲线，以及如何选取形状参数来使曲线达到最优化，如何使曲线在获得更大的自由度同时不增加操控的复杂度等问题。

[1] 施法中. 计算机辅助几何设计与非均匀有理B样条[M]. 北京: 高等教育出版社, 2001: 12-24. SHI F Z. CAGD & NURBS[M]. Beijing: Higher Education Press, 2001: 12-24 (in Chinese).

[2] POPIEL T, NOAKES L. C2 spherical Bézier splines[J]. Computer Aided Geometric Design, 2006, 23(3): 261-275.

[3] De Casteljau P. Outillages méthodes calcul[R]. Paris: André Citroën Automobiles, 1959.

[4] KIM M J, KIM M S, SHIN S Y. A compact differential formula for the first derivative of a unit quaternion curve[J]. The Journal of Visualization and Computer Animation, 1996, 7(1): 43-57.

[5] CURTIS M L. Matrix groups[M]. New York: Springer, 1979.

[6] KIM M S, NAM K W. Interpolating solid orientations with circular blending quaternion curves[J]. Computer-Aided Design, 1995, 27(5): 385-398.

[7] Kim M J, Kim M S, Shin S Y. A general construction scheme for unit quaternion curves with simple high order derivatives[C]//SIGGRAPH’95 Proceedings of the 22nd Annual Conference on Computer Graphics and Interactive Techniques. New York: ACM Press, 1995: 369-376.

[8] TAN J Q, XING Y, FAN W, et al. Smooth orientation interpolation using parametric quintic-polynomial-based quaternion spline curve[J]. Journal of Computational and Applied Mathematics, 2018, 329: 256-267.

[9] SHOEMAKE K. Animating rotation with quaternion curves[J]. ACM SIGGRAPH Computer Graphics, 1985, 19(3): 245-254.

[10] KLETTE R, KOZERA R, NOAKES L, et al. Geometric properties for incomplete data[M]. Dordrecht: Kluwer Academic Publishers, 2006: 77-101.

[11] CROUCH P, KUN G, LEITE F S. The de casteljau algorithm on lie groups and spheres[J]. Journal of Dynamical and Control Systems, 1999, 5(3): 397-429.

[12] LUO Z X, WANG Q, FAN X, et al. Generalized rational Bézier curves for the rigid body motion design[J]. The Visual Computer, 2016, 32(9): 1071-1084.

[13] HOSCHEK J，SEEMANN G. Spherical splines[J]. ESAIM: Mathematical Modelling and Numerical Analysis, 1992, 26(1): 1-22.

[14] 王仁宏, 李崇君, 朱春钢. 计算几何教程[M]. 北京: 科学出版社, 2008: 79-83. WANG R H, LI C J, ZHU C G. Computational geometry tutorial[M]. Beijing: Science Press, 2008: 79-83 (in Chinese).

[15] Wang W P, Qin K H. Rational spherical curve interpolation[C]//Proceedings of CAD/Graphics’97. Beijing: International Academic Publishers, 1997: 447-449.

[16] PARK F C, RAVANI B. Bézier curves on Riemannian manifolds and lie groups with kinematics applications[J]. Journal of Mechanical Design, 1995, 117(1): 36-40.

[17] 王倩. 球面曲线插值问题及不变量的研究与应用[D]. 大连: 大连理工大学, 2016. WANG Q. Research and applications on interpolation and invariants of spherical curves[D]. Dalian: Dalian University of Technology, 2016 (in Chinese).

[18] KIM M J, KIM M S, SHIN S Y. A C/sup 2/-continuous B-spline quaternion curve interpolating a given sequence of solid orientations[C]//Proceedings Computer Animation’95. New York: IEEE Press, 1995: 72-81.

[19] 罗钟铉. 非线性样条函数[D]. 大连: 大连理工大学, 1991. LUO Z X. Nonlinear spline function[D]. Dalian: Dalian University of Technology, 1991 (in Chinese).

[20] HOSCHEK J. Bézier curves and surface patches on quadrics[M]//Mathematical Methods in Computer Aided Geometric Design II. Amsterdam: Elsevier, 1992: 331-342.

[21] 陈维桓. 微分几何[M]. 北京: 北京大学出版社, 2006: 7-16. CHEN W H. Differential geometry[M]. Beijing: Peking University Press, 2006: 7-16 (in Chinese).

The construction of spherical interpolation splines with local properties

WANG Qian1, PAN Le1, ZHANG Jie-lin2, PENG Xing-xuan1

(1. School of Mathematics, Liaoning Normal University, Dalian Liaoning 116021, China; 2. School of Mathematics, Jilin University, Changchun Jilin 130023, China)

The high dimensional spherical spline curves fitting technology has received wide attention in computer animation and inertial navigation. In practical applications, spline curves are usually required to interpolate the given data points with certain continuity and local properties. Thus, the previous methods are limited in certain regards. For this reason, a new method, based on spherical Bézier curves, of constructing spherical spline in arbitrary dimensional space was proposed. Firstly, the higher order derivative vectors at the interpolation points were fitted by a reflection. Then, necessary and sufficient conditions for2Hermite interpolation were given. Finally, the2spherical Bézier spline was constructed, using only interpolation points. The proposed method exhibitslocal properties. The disturbance of some points will not impact other parts of the spline. The splines possess explicit expressions not involving nonlinear equations. Numerical experiments show that the method can be widely applicable and efficient.

spherical spline; spherical Bézier curve; interpolation; parameter continuity; rigid body motion

TP 391

10.11996/JG.j.2095-302X.2021020230

A

2095-302X(2021)02-0230-07

2020-09-26；

26 September，2020；

2020-10-18

18 October，2020

国家自然科学基金项目(61702244，61720106005，61572105)；辽宁省教育厅项目(L201783642)

National Natural Science Foundation of China (61702244, 61720106005, 61572105); Liaoning Provincial Education Department Project (L201783642)

王 倩(1982-)，女，辽宁大连人，讲师，博士。主要研究方向为计算几何。E-mail：wangqian603603@sina.com

WANG Qian (1982-), female, lecturer, Ph.D. Her main research interest covers computational geometry. E-mail：wangqian603603@sina.com