基于周期性晶格的3D打印模型轻量化方法
2021-05-13肖文磊王志明王世平
肖文磊,王志明,王世平,赵 罡
基于周期性晶格的3D打印模型轻量化方法
肖文磊,王志明,王世平,赵 罡
(北京航空航天大学机械工程及自动化学院,北京 100191)
为了获得3D打印模型节材效果和优化的物理力学性能,从晶格的形状多变性出发,提出了一种基于晶格的3D打印轻量化结构生成方法,由此产生的轻量化结构用来替代给定模型的实体空间。首先,提出了一种通用的晶格描述方法,进而对晶格的几何和拓扑特征进行个性化设计。其次,通过在模型包围盒内周期性排列晶格单元,构造出了实体建模所依附的拓扑骨架结构。接着,采用了一种基于网格拼接的直接构建STL模型的几何建模方法,其无需布尔运算即能快速获得网格质量可控的晶格实体结构。通过实物打印验证了适用于晶格结构的3D打印成型工艺。对5种典型晶格的几何和力学特性进行了对比分析,并作为晶格设计选用的初步依据。结果证明,该方法在实现节材和提高模型强重比的同时,达到了保证轻量化模型的可打印性、自平衡性以及力学性能可优化等目标。相较于以往的方法,具有多变性和效率优势,适合各种工程应用。
3D打印;轻量化模型;周期性晶格;实体建模;实物打印
3D打印是一种先进的快速成型工艺,即对熔融材料进行逐层叠加来构建预先设计的数字模型。3D打印在复杂零件制造领域有着重要的应用价值。一般对于任何复杂的结构均能一次性成型,且无需工装模具,这使得具有复杂几何的轻量化结构突破了可制造性束缚。在3D打印模型中添加多孔的轻量化结构既能提升结构各方面性能,又能有效节省打印成本。近年来,国内外研究人员针对轻量化结构提出了许多设计方法,大多采用自顶向下或自底向上的技术方案。
自顶向下的方法以实现整体结构的轻量化为设计目标,对单元结构体的形状和尺寸等关键参数不做主动控制。WANG等[1]提出了一种轻量化的蒙皮桁架结构来掏空给定模型。该蒙皮桁架结构由空间中随机分布的节点和圆柱杆构成,不仅保证了模型的承载能力,通过求解稀疏优化方程来减少杆的数量又进一步减少了打印耗材,但未将杆长作为设计变量。WANG和ROSEN[2]基于参数化建模技术设计了一种轻量化桁架结构生成方法。该方法利用零件的近似参数化表面及偏移来构造参数化体积,并在决定节点位置后将不同节点按给定规则进行连接。但其需人工完成费时费力的曲面近似参数化操作。李大伟等[3]根据对模型脆弱区域的分析使用截面连续变化的隐函数曲面生成了模型内部填充结构。即通过曲面函数参数控制来实现密度和梯度可控,且具有连通性利于高效制造,但单元种类仅局限于一种。LU等[4]通过三维Voronoi图和模型应力图来定义模型内部优化的变密度不规则蜂窝镶嵌结构。ZHANG等[5]以计算出的模型中轴作为骨架,用与其连接的树状分支构造模型边界面下的填充结构,使模型以最少材料来承受不同方向的外部载荷。自顶向下方法最突出的缺点是单元拓扑不规则且难以控制,缺乏设计灵活性导致适用面窄且优化空间小。
自底向上的方法是选用各种晶格单元来设计轻量化结构。首先,晶格结构的设计更加灵活,比如通过调整节点位置和拓扑连接关系可获得不同形状的晶格。其次,根据不同的设计要求,通过调整晶格尺寸或选用不同的晶格形状,既能获得显著的减重效果,又能保证力学性能不受影响。针对如何生成晶格支撑结构,郑晓龙等[6]模仿自然界细胞生长方式设计了自然生长算法,有效降低了打印材料用量。该算法以初始单元作为母细胞,逐层向外扩展填充单元。但是每次单元生成均需计算所有相邻单元,导致生成过程较耗时。为了获得强度及孔隙均匀分布的骨组织支架结构,CHEAH等[7-8]研究并设计了基于建模软件的晶格阵列结构生成方法。首先创建了各种晶格细胞的参数化库以满足各类设计需求;随后通过Pro/E二次开发将晶格单元体组装成所需形状和尺寸的周期晶格结构。若晶格结构过于复杂,将造成大量的计算机资源开销。为了解决CAD软件在复杂晶格结构的设计和建模上能力不足的问题,CHEN[9]受纹理渲染技术的启发提出了3D纹理贴图晶格填充结构设计方法,其采用了混合的实体建模方法。首先利用实体建模和网格剖分构造每根杆的STL模型,然后将其直接添加到整体结构中。虽然该方法在一定程度上解决了复杂晶格结构建模低效的问题,但中间处理仍需ACIS的支持,该方法仍存在一定局限性。
本文提出了一种基于晶格的模型内部轻量化结构构造方法。首先由晶格结构的元素组成定义了其数据模型;提出了晶格数字化方法,以提高冗余数据去除的效率;为适应各种晶格的设计需求,采用通用文件格式保存晶格拓扑;结合所选择的晶格,在模型包围盒内创建了空间框架拓扑结构;采用一种快速高效的几何建模方法,并利用传统的裁剪算法,得到了轮廓形状与模型边界一致的分支结构的STL模型。给出了适用于晶格填充模型的3D打印工艺;最后,为指导晶格的选用设计,对5种典型晶格的关键性能指标进行了对比分析。
1 晶格结构通用描述方法
1.1 晶格数据模型
对模型进行轻量化设计时,使用晶格填充结构既能去除大量材料又可保证结构的完整性和强度要求。晶格有许多种类,图1是几种常见的晶格。各类晶格具有不同的几何形状,而且任意一种晶格本身也包含多个设计参数。因此,晶格的通用模型需保证可互换性。

图1 几种常见的晶格拓扑


图2 晶格局部坐标系
节点和杆构成了晶格的拓扑结构。为了建立完整的晶格模型,还需描述晶格的各种几何特征。晶格杆具有不同的横截面形状,以适应不同的设计需求。例如,圆形截面杆的强度一般要高于四边形截面杆。因此,前者更适合于高强度结构,而后者则可以借助其柔性特性实现能量吸收的功能[10]。对于正多边形或圆形的横截面形状,其尺寸都可表示成参数。晶格整体还具有大小属性,表示,和等3个方向上的投影长度= (L,L,L)。其中每个方向尺寸均互不干涉,使晶格缩放到任何想要的大小。改变不同的参数值即可实现对一种晶格的个性化配置。
根据以上分析,本文提出了图3所示的晶格通用数据模型。该模型可定义具有不同拓扑和几何特征的晶格结构。一个晶格由局部坐标系中的一系列节点和一系列杆定义。每个节点对应一个空间坐标位置和按顺序指定的一个编号。每根杆由无序的两端节点的编号来定义。杆的横截面包括形状和尺寸2个参数。

图3 晶格通用数据模型
1.2 晶格数字化处理
由选定的晶格拓扑所生成的晶格阵列中,相邻晶格的节点和杆在拼接处发生重叠。为了保证元素唯一性,必须进行去重处理。而在实际应用中,晶格大小存在各种可能性,比如节点坐标值为浮点数。由于计算机对浮点数有存储规则的限制,因此在数据比较时要考虑浮点数的精度问题。一般以预先设置的非零偏差来做相等判断。需确保晶格的大小不能小于该偏差,否则节点重合判断将输出错误结果。此外,浮点数的运算性能也不及整数,比如加减运算指令。因此,为了减少计算量并提高对象表示的准确度,提出了一种将节点坐标值数字化为整数的方法。
假定晶格,和3个方向上节点间最小间距min=(D,D,D),并允许其包含浮点数分量。那么对于晶格节点V= (,,),经过数字化处理后V= (/D,/D,/D),这时V的分量均转换为整数。以图4为例,各方向上网格线间距允许不同,每个晶格节点用网格线交点位置的整数值编址,即相当于将整个晶格以比例因子进行缩放变换。其好处是去冗余数据时可直接对这些整数做相等判断。对数字化后的晶格进行逆变换即可恢复晶格的原始尺寸。

图4 对一种二维晶格划分网格
1.3 晶格拓扑定义
不同晶格的本质区别在于其拓扑结构。因此在初始设计时仅需给出晶格的拓扑定义即可唯一的确定该晶格。为了灵活适应各种应用,本文利用一种通用的文件格式建立了晶格库,并预设了一些常见的晶格拓扑。对通用文件格式的要求是便于编辑且易于理解。为此,本文使用JSON文件来存储晶格拓扑,并作为输入文件提供给后续处理。例如,X形晶格的拓扑定义如图5所示,其中MouldTolerance数组表示晶格数字化处理中使用的最小间距值。

图5 X形晶格拓扑定义JSON文件((a) X形晶格拓扑定义文件;(b) X形晶格拓扑)
2 空间框架拓扑结构生成算法
结合预先选定的晶格单元,本文又生成了一种内部连续且单元均布的空间框架结构,其用来构造给定的CAD模型的内部结构。在该空间框架结构中,所有单元使用同一种晶格拓扑,且在三维空间中周期性重复出现。空间框架结构的关键参数,如孔隙率和3个方向上的尺寸,可通过操控晶格单元进行设置。本文以选定的晶格为初始单元,向3个正交方向循环复制,逐渐充满由模型坐标范围确定的包围盒。图6是基于该算法获得的2种晶格阵列拓扑结构。

图6 2种框架拓扑结构((a)基元为立方晶格;(b)基元为面心立方晶格)
该算法包含2个阶段。第一阶段是晶格数字化处理,此阶段输出的晶格数据将作为第二阶段的输入。由于框架仅由单一类型的晶格组成,所以框架尺寸由晶格尺寸乘晶格个数来指定。这里假定3个正交方向上的晶格个数分别为N,N和N。第二阶段是按一定规则复制处理后的晶格单元。以平面区域中的二维晶格为例,复制过程如图7所示。在图中,沿向放置晶格,一次循环填满一行,到达行尾时,填充位置返回下一行的最左边,再进行填充。对每轮循环分别进行如下处理:
步骤1.首先判断沿当前方向复制的晶格是否已经超出了设计域边界。例如,若当前沿正方向复制,记该方向当前循环次数为。若≥N,则停止复制,复制方向转到方向;
步骤 2. 若当前三重循环次数=(N,N,N),则以作为晶格的建模基准点;
步骤3.根据晶格的建模基准点和晶格自身局部坐标系,计算晶格节点的局部坐标;
步骤4.最后将晶格节点变换到真实尺寸框架所在的全局坐标系,即得到了晶格真实的节点位置矢量。
通过上述处理可得到框架中所有节点的坐标位置,再结合原始晶格中节点的连接关系以及去重处理,最终得到了以无向图表示的完整框架。因此,框架的基本数据模型同样是由节点和杆2类信息组成。

图7 晶格阵列的二维示意图
3 晶格结构实体建模
基于框架所构造的实体特征是包含了大量杆单元的分支结构。传统方法是利用CAD软件或几何造型内核如ACIS生成桁架结构实体模型,然后转换为可用于制造的STL模型[11]。这种方法通过布尔运算处理分支处的重叠部分,效率较低的同时又带来了大量的计算机资源开销。三角形网格被广泛用于几何物体的表示,本文采用了基于三角形网格的快速的几何建模方法,不需要布尔运算即可根据节点和轴线生成无重叠的三角网格实体结构。图8为该方法生成的三角网格结构的例子。其主要处理步骤如下:
步骤1.建立如图9所示的圆周。对于每一个节点,建立圆心在轴线上且所在平面与轴线垂直的圆周,允许各个圆周的半径不一致。然后根据所需的网格质量在圆周上的离散位置进行均匀取样,且取样点将用于构造杆和节点凸包的三角网格。圆周与节点间距离D的计算是关键步骤,要求该分支处的所有杆不会相互干涉,其距离为

其中,R为杆的横截面尺寸,大小不限;为该分支处不同杆间的最小角度;为大于1的比例因子,确保杆在节点处不会重叠。
步骤2.在每一个节点位置上生成封闭凸包三角网格。基于对应于节点的圆周上的离散采样点,结合点集三角化技术构造封闭的三角网格。
步骤3.去除圆周平面上的三角形网格。该步骤用于保证节点凸包和杆能够形成连通的网格。
步骤4.在圆周之间构造杆的网格。引用轴线上2个相对的圆周来构造不含端面的杆网格,其截面边数等于圆周上的点数。由于分支处的凸包与杆是基于相同的圆周得到的,因此并不需要额外的处理即得到了无自交和间隙的整体结构的三角网格模型。
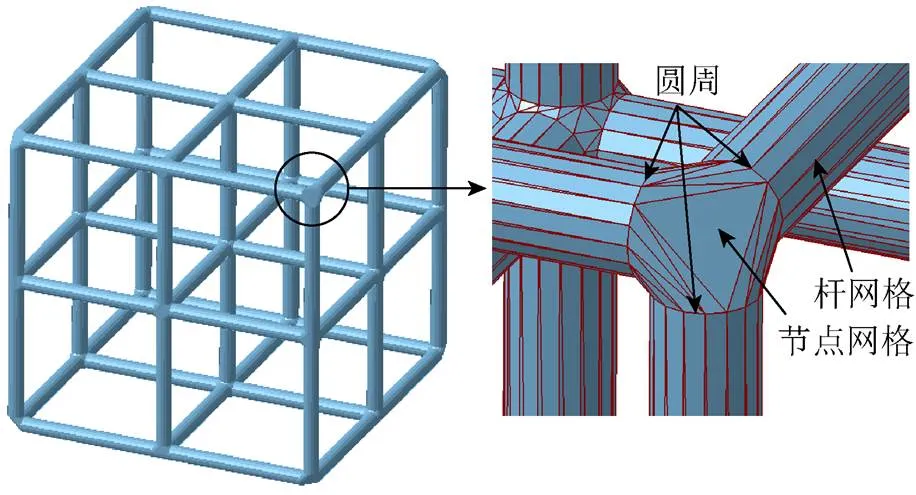
图8 由立方晶格组成的分支实体结构

图9 与一个节点对应的3个圆周
该方法由于采用三角形网格近似表示圆柱杆和球形节点,当近距离观察时会看到一定程度的形状失真现象。但网格质量并非固定不变,可通过增加圆周离散化点数获得更高的网格光顺度,进而提高模型的力学性能,如图10所示。LIN等[12]提出了另一种更优的快速建立平滑分支结构的方法。该方法首先生成了复杂分支形状的连通图,随后将几何信息强加于连通图上从而导出分支结构的高分辨率网格。并在树形结构建模和血管网可视化等方面进行了验证,均获得了高网格质量及实时快速兼备的效果。

图10 圆周采样点个数对网格质量的影响((a) 16个采样点;(b) 32个采样点)
为了在模型内部生成晶格实体模型,首先利用待填充STL模型裁剪其包围盒内的框架拓扑结构。接着,对裁剪后的框架拓扑利用上述实体化步骤进行加厚处理。图11显示了兔子模型的X形晶格填充结果。由于本文未研究如何生成给定模型的外壳,所以最后仅保留了裁剪成模型边界形状的分支结构。

图11 在兔子模型中添加晶格结构
4 晶格模型的3D打印工艺
应用不同的单元拓扑可能会在晶格结构中生成0~90°不等的悬垂几何特征。根据FDM打印工艺要求,在打印过程中必须在悬垂结构下方添加支撑结构来完成打印,结束后将支撑结构与原始模型进行分离。
依据不同的去除方式可将支撑结构分为2类。①采用与模型相同或类似的材料打印支撑结构,模型打印完成后需借助外力去除,如树状支撑杆结构后续处理比较繁琐和费时,由于操作失误也可能破坏原模型表面平整度。②支撑结构采用有别于模型材料的特种材料。如水溶性支撑材料,放到水里一段时间即可去除,无需施加外力。可提高水的温度或改用冲洗的方式缩短材料的溶解时间。
晶格填充模型在不同高度位置都存在悬垂杆,因此对于上述2种方法,只能采用后者即水溶性材料来提供支撑。为了研究基于水溶性支撑的FDM工艺打印晶格结构的可行性,本文在Ultimaker S5 打印机上进行了具有不同单元拓扑的晶格结构的打印实验。该打印机安装了2个打印喷头,分别挤出模型成型用的PLA材料和支撑用的PVA水溶性材料。打印结束后将晶格放到温水浸泡去除支撑,打印实物如图12所示。经观察,去除支撑后的晶格尺寸、外观、质量和细节均较好,说明了利用该工艺打印晶格是完全可行的。

图12 晶格模型的FDM打印效果((a)打印后带水溶支撑;(b)去除水溶支撑后)
5 不同晶格拓扑的主要特性
晶格结构具有优秀的力学性能以及吸能减重等物理优势,前人已经在各种应用中对晶格进行了讨论。在再生医学领域,晶格中规则的孔洞能够在促进组织生长的同时提供结构支撑,为设计符合功能要求的骨组织支架结构提供了新思路[13]。车辆保险杠和产品包装箱等常采用吸能多孔材料使被保护对象免遭破坏。HABIB等[14]对不同晶格拓扑的力学行为分析表明,一些以弯曲为主的晶格结构具有良好的耗能特性。具有轴向变形梁的拉伸主导的晶格具有更高的强度,而且内部中空重量轻,可作为夹层结构满足飞机机翼等航空航天零件对高强重比的要求。可见,晶格作为性质可控的微观结构适用于广泛的工程应用。
通过研究不同晶格拓扑的特性差异,来指导具体应用中的晶格选用策略。本文所获得大尺度晶格阵列结构中仅包含单一的晶格拓扑,而且单元周期性均匀分布,可近似视为各向同性的均质材料。因此可用晶格个体替代晶格阵列结构作为性质研究的对象,即利用本文算法生成的具有相同边长和杆径的5种晶格拓扑。评估的性质包括重量、孔隙率和峰值应力。孔隙率的计算方法是用晶格的孔隙体积除以其名义体积[13]。为简化计算,将名义体积用晶格包围盒体积近似。利用Ansys软件分析了各种晶格在静态单向加载下的压缩行为。选用3D打印专用的PLA塑料作为Ansys材料参数输入。在晶格底面添加固定支撑,在顶面作用垂直于底面的均布载荷,载荷大小为1。网格采用自动划分法,其他参数均保持默认设置。按照以上配置对5种晶格模型分别进行求解,计算结果以应力云图显示。以立方体晶格为例,其载荷和约束设置、求解结果如图13所示。

图13 X形晶格的有限元分析模型((a)载荷和约束设置;(b)有限元分析结果)
5种晶格拓扑的峰值应力及其他特性的具体数值见表1。经过观察可知,晶格孔隙率随晶格重量的增加而减小,其中X形晶格的孔隙率最大。从X形晶格到八角点阵晶格,强度随着重量增加而增大。X形晶格由于以杆弯曲变形为主,强度和刚度较低,相对而言具有更好的吸能特性。八角点阵晶格结构致密,更适合承受大载荷和不变形。另一方面,面心立方晶格重量最高,强度反而比立方晶格低,这是由于面心立方晶格更易出现应力集中。由此可见,晶格拓扑、孔隙度和强度之间存在着复杂的耦合关系。因此,对于本文未给出的其他晶格拓扑,除了几何特征外还要结合力学分析才能进行准确的评估和设计。
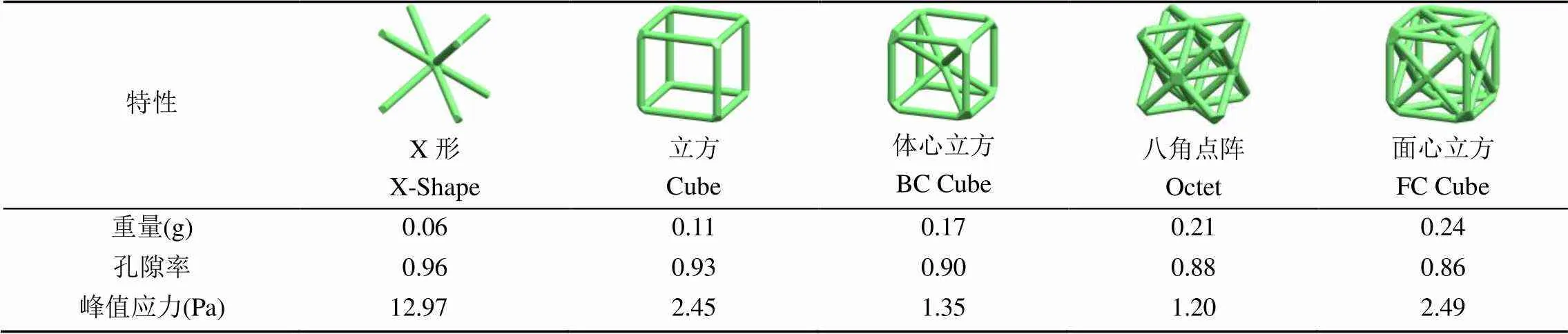
表1 5种常见晶格拓扑的特性对比
注:杆直径均为1 mm;晶格边长均为10 mm
6 应用实例
本文算法已在Visual studio 2012环境中采用C++语言得以实现,并形成了可移植的轻量级软件内核。为了验证其有效性和高效性,在CPU为Intel(R) Core(TM) i5-4200U(1.6 GHz),内存为4 G,Windows 8.1操作系统的PC机上进行了测试。
在设计自由度方面,三维维诺孔洞方法[4]和蒙皮桁架方法[1]均不能定制单元拓扑,而本文方法允许的单元拓扑几乎没有限制。图14展示了本文的软件内核分别为体心立方、X型和立方体晶格单元生成的3种晶格阵列实体结构。事实上,本文采用的晶格填充算法完全不受晶格拓扑结构的约束。在由图15立方体晶格组成的晶格阵列结构中,晶格的3个正交方向分别设定了不同的尺寸。图16为杆横截面分别是圆形、六边形和四边形的实体结构。图17中杆的半径各不相同,这是由于本文实体生成步骤中的圆周采用了不同的半径值。进一步说明了本文算法的有效性和极高的灵活性。
在力学性能方面,蒙皮桁架结构只在模型表皮存在支撑杆,内部完全空心,因此不能保证模型较高的强度。而本文则不存在这种缺陷,同时晶格单元的定制能力为各种力学性的实现提供了无限的潜力。

图14 3种不同晶格组成的网状阵列结构

图15 晶格单元尺寸可以不统一

图16 圆形、四边形和六边形截面的晶格实体结构

图17 杆半径的差异化
在可打印性方面,维诺方法在模型内部掏出的孔洞是完全封闭的,无法使用需要支撑的打印工艺。而且孔洞大小和位置的随机性可能破坏模型的物理稳定性,打印时需要矫正模型的摆放位置来确保稳定。本文生成的晶格结构中的单元彼此连通,有利于打印碎屑和支撑材料的去除。同时通过实物打印验证了基于水溶性支撑的FDM打印工艺的可行性。而且由于单元均匀分布,基本不会影响模型重心位置,从而保持了模型本身的打印平衡性。
由于本文采用均匀分布的晶格基元逼近零件边界,若采用较大的晶格尺寸可能会丢失模型中的细长特征。其解决方法是不断减小晶格尺寸以获得理想的逼近精度,如图18所示。但该方案反过来又会降低轻量化效果,因此需要根据具体应用进行适当的权衡。

图18 晶格边长对填充精度的影响((a)边长15 mm;(b)边长10 mm;(c)边长5 mm)
为了验证本文算法的高效性,与目前市场上比较流行的NX软件中的晶格设计功能进行比较。待填充对象是半径为100 mm的球实体模型,使用的晶格类型为X形晶格,其边长等于10 mm×10 mm× 10 mm,杆半径为1 mm。在NX的晶格模块中设定了其最高网格精度值。图19为本文软件与NX软件的建模结果,建模时间分别为2.7 s和126.0 s。可见,本文软件生成的网格更加光滑,且速度也远远快于NX软件,其高效性突出。

图19 2款软件建模结果对比((a)本文软件填充结果;(b) NX软件填充结果)
7 结束语
本文针对现有的各种3D打印模型轻量化方法存在的问题,结合高效的实体建模技术提出了基于周期性分布晶格的模型快速轻量化方法。
该方法首先构造晶格基元的数据模型,并用一种简单易读的文件格式对晶格拓扑进行存储和设计。接着根据给定的晶格类型及其在各方向分布的个数,在3个正交方向对该晶格循环拼接来获得一种规则的骨架结构。最后采用了一种高效的网格实体建模方法。这种方法基于骨架结构的节点和边生成各自的保留对应缺口的三角网格,且无需使用布尔运算即可实现各个位置网格的水密性叠加。最终获得了STL文件格式表达的轻量化结构,可直接用于后续打印制造。同时给出晶格的3D打印工艺,并对不同晶格的主要特性进行了对比分析。通过实例对本文的方法进行验证,结果表明,本文方法可同时达到节省材料、维护物理稳定性、保证可打印性以及为力学性能优化提供多种手段的目标,算法有效、灵活且具有高效的优势。
但一些问题仍有待进一步研究。首先,本文的轻量化结构目前是取代了模型的全部体积,但未考虑模型表皮偏置问题;其次,试验的3D打印工艺是沿高度方向逐层堆积成型,若层间结合不够牢固,可能导致晶格切向强度较差,文献[14]给出的称为MJF的新型3D打印技术可能是一种更优的打印方案;最后,如何应用晶格尺寸差异化技术来解决轻量化和逼近精度之间的矛盾也是未来的研究方向之一。
[1] WANG W M, WANG T Y, YANG Z W, et al. Cost-effective printing of 3D objects with skin-frame structures[J]. ACM Transactions on Graphics, 2013, 32(6): 1-10.
[2] WANG H Q, ROSEN D. Computer-aideddesign methods for additive fabrication of truss structures[EB/OL]. [2020-11-24]. https://www.researchgate.net/publication/228545192_Computer-aided_design_methods_for_additive_fabrication_of_truss_structures.
[3] 李大伟, 戴宁, 姜晓通, 等. 密度感知的3D打印内部支撑结构轻量化建模[J]. 计算机辅助设计与图形学学报, 2016, 28(5): 841-848.LI D W, DAI N, JIANG X T, et al. Density aware internal supporting structure light-weighting modeling of 3D printed objects[J]. Journal of Computer-Aided Design & Computer Graphics, 2016, 28(5): 841-848 (in Chinese).
[4] LU L, SHARF A, ZHAO H, et al. Build-to-last: strength to weight 3D printed objects[J]. ACM Transactions on Graphics, 2014, 33(4): 1-10.
[5] ZHANG X L, XIA Y, WANG J Y, et al. Medial axis tree—an internal supporting structure for 3D printing[J]. Computer Aided Geometric Design, 2015, 35-36: 149-162.
[6] 郑晓龙, 刘远, 郑国磊, 等. 激光选区熔化工艺晶格支撑结构快速建模[J]. 图学学报, 2018, 39(5): 879-885.ZHENG X L, LIU Y, ZHENG G L, et al. Rapid modeling of lattice support structures for selective laser melting[J]. Journal of Graphics, 2018, 39(5): 879-885(in Chinese).
[7] CHEAH C M, CHUA C K, LEONG K F, et al. Development of a tissue engineering scaffold structure library for rapid prototyping. part 2: parametric library and assembly program[J]. The International Journal of Advanced Manufacturing Technology, 2003, 21(4): 302-312.
[8] CHEAH C M, CHUA C K, LEONG K F, et al. Development of a tissue engineering scaffold structure library for rapid prototyping. part 2: parametric library and assembly program[J]. The International Journal of Advanced Manufacturing Technology, 2003, 21(4): 302-312.
[9] CHEN Y. 3D texture mapping for rapid manufacturing[J]. Computer-Aided Design and Applications, 2007, 4(6): 761-771.
[10] CHEN Y. A mesh-based geometric modeling method for general structures[C]//Design Engineering Technical Conferences and Computers and Information in Engineering Conference. Philadelphia: ASME, 2006: 1-13.
[11] WANG H Q, CHEN Y, ROSEN D W. A hybrid geometric modeling method for large scale conformal cellular structures[C]//International Design Engineering Technical Conferences and Computer and Information in Engineering Conference. Philadelphia: ASME, 2005: 1-7.
[12] LIN J C, JIN X G, WANG C C L. Fusion of disconnected mesh components with branching shapes[J]. The Visual Computer, 2010, 26(6-8): 1017-1025.
[13] EGAN P F, GONELLA V C, ENGENSPERGER M, et al. Computationally designed lattices with tuned properties for tissue engineering using 3D printing[J]. PLoS One, 2017, 12(8): e0182902.
[14] HABIB F N, IOVENITTI P, MASOOD S H, et al. Fabrication of polymeric lattice structures for optimum energy absorption using Multi Jet Fusion technology[J]. Materials & Design, 2018, 155: 86-98.
A light weight method of 3D printing model based on periodic cell
XIAO Wen-lei, WANG Zhi-ming, WANG Shi-ping, ZHAO Gang
(School of Mechanical Engineering and Automation, Beihang University, Beijing 100191, China)
In order to obtain the material-saving effect and optimized physical and mechanical properties of 3D printing models, starting with the lattice shape variability, a lattice-based 3D printing lightweight structure generation method was proposed. The resulting lightweight structure was employed to replace the solid space of the given model. Firstly, a general unit cell description method was proposed to design the geometric and topological characteristics of unit cell. Secondly, the topology skeleton structure, on which the solid modeling was based, was constructed by periodically arranging lattice units in the bounding box of the model. Finally, a geometric modeling method based on mesh splicing was utilized to directly construct the STL model, and the lattice solid structure with controllable mesh quality can be obtained quickly without Boolean operation. The 3D printing molding process suitable for lattice structure was verified through object printing. Comparisons and analyses were conducted on the geometrical and mechanical properties of the five kinds of typical lattices serving as a preliminary basis for lattice design and selection. The examples show that this method can not only save material and improve the strength-weight ratio of the model, but also guarantee the printability, self-balancing, and the optimization of mechanical properties of the lightweight model. Compared with previous methods, it is advantageous in variability and efficiency and is applicable to various engineering applications.
3D printing; lightweight model; periodic lattice; solid modeling; object printing
TP 751.1
10.11996/JG.j.2095-302X.2021020263
A
2095-302X(2021)02-0263-08
2020-09-22;
22 September,2020;
2020-11-16
16 November,2020
肖文磊(1984-),男,江西井冈山人,副教授,博士。主要研究方向为3D打印晶格结构建模和智能制造技术等。 E-mail:xiaowenlei@buaa.edu.cn
XIAO Wen-lei (1984-), male, associate professor, Ph.D. His main research interests cover 3D printing lattice structure modeling and intelligent manufacturing technology, etc. E-mail:xiaowenlei@buaa.edu.cn
