J-TEXT装置上的三维磁场分析研究
2021-05-13刘永超龚学余杨文军曹锦佳
刘永超,龚学余,*,杨文军,向 东,曹锦佳
(1.南华大学 电气工程学院,湖南 衡阳 421001;2.南华大学 核科学技术学院,湖南 衡阳 421001)
0 引 言
能源危机问题是当今最主要的问题,可控核聚变是彻底解决这场危机的有效途径之一。但可控核聚变需要将等离子体加热到大约1亿摄氏度,常规的容器不能承受如此高温,所以需要很好的约束反应物质。常用的约束手段有两种,惯性约束和磁约束。惯性约束是通过强激光电子束对聚变材料进行作用,在极短的时间内让物质达到高温高密度状态,从而发生聚变反应。磁约束聚变是利用强磁场来约束高温等离子体态的聚变核燃料,持续可控的发生核反应释放能量,与瞬间释放能量的聚变方式相比该方案更有利于商用发电[1]。受控磁约束聚变最具代表性的位形有:托卡马克和仿星器。而托卡马克位形被认为是最具前景的。目前国际上在建的ITER[2](international thermonuclear experimental reactor)以及国内正在立项设计的CFETR[3](China fusion engineering test reactor),正是采用的托卡马克位形。
由于托卡马克装置是轴对称系统,为了计算方便,利用其环向对称性,L.L.LAO等人采用的二维模型[4]。袁保山等人对铁芯结构的托卡马克装置,从研究等离子体区域极向场的角度考虑,近似把中心柱看作无限长,研究了铁芯的存在对极向场的影响[5]。E.R.Solano等人建立了卷轴模型,计算了铁芯在非饱和情况下对极向场的影响,给出了极向场的解析表达式[6]。杜世俊等人在研究铁芯对平衡计算的影响时,把铁芯对平衡的影响看作是外部极向场线圈镜像电流的作用,巧妙地将问题转化为空气铁芯的磁流体力学(magnetohydrodynamics,MHD)方程的求解[7]。以上结构都忽略环向不对称性,视为环形对称,皆可看成二维结构。程际等人建立带铁芯的极向磁场线圈三维数值模型,计算并研究铁芯托卡马克的三维磁场的极向分量在环向上的不对称性[8]。
理想的托卡马克磁场位形是二维结构,主要包含环向磁场和极向磁场。但是,电流母线接头、环向场线圈和极向场线圈的安装偏差以及铁磁性质的物质等等都会使磁场不再对称,产生径向磁场(误差场),这会使得磁场位形变成三维结构[9-10]。误差场的存在会对托卡马克装置产生极大影响,例如导致撕裂模锁模,甚至引发破裂[11]。故而研究磁场位形的三维结构显得尤其重要。
J-TEXT(joint texas experimental tokamak)[12]是典型的圆截面铁芯中型托卡马克装置,其大半径R=1.05 m,等离子体小环半径约0.35 m,纵场最大磁感应强度Bt=3.0 T,等离子体最大电流I=400 kA,等离子体中心密度为5.8×1019m-3,中心电子温度0.85 keV,中心离子温度0.45 keV。
本论文主要是基于J-TEXT平衡参数,利用VMEC程序求解得到J-TEXT装置的三维磁场位形。第1节介绍了VMEC程序的工作原理,给出了等离子体在磁面坐标下的Grad-Shafranov方程。第2节中通过VMEC程序仿真得到结果,论证VEMC程序嵌入J-TEXT装置的可行性。第3节分析了等离子体压强、等离子体电流对三维磁场的影响。
1 物理模型
1.1 VMEC程序简介
1.2 平衡方程
容易得到,大半径坐标系(R,φ,Z)下轴对称模型的等离子体平衡Grad-Shafrov方程[14-15]:
(1)
为了获得通量坐标系下等离子体平衡Grad-Shafrov方程,人们通常用标准方法求解网格上的(R,φ,Z)的Grad-Shafrov方程,然后映射得到(ψ,θ,ζ)坐标下的Grad-Shafrov方程。
通量坐标系下的等离子体平衡Grad-Shafrov方程[16-17]:
(2)

2 VMEC程序仿真平衡参数与结果分析
2.1 平衡参数
VMEC是三维平衡求解器,在提供初始等离子体边界、等离子体压强剖面、旋转变换剖面和外部电流的情况下,程序将在合理的时间内计算整个环形等离子体的平衡位形。
本文选取J-TEXT装置第1059184炮平衡文件数据,基于平衡文件中压强剖面数据作为VMEC程序的输入参数,如图1所示。等离子体压强在磁轴位置最大,向边界递减,在边界处趋于零。
由于旋转变换τ与安全因子q的关系为:τ~1/q。旋转变换τ可以通过安全因子q来计算求得。同压强剖面,基于平衡文件中安全因子剖面数据作为VMEC程序的输入参数,如图1所示。安全因子q的径向剖面通常在磁轴处或靠近磁轴处有最小值,并向外增大。在大纵横比和圆形截面的情况下,q简单地由环向电流密度剖面j(r)决定。因旋转变换τ与安全因子q成反比例关系,则旋转变换的径向剖面通常在磁轴处或靠近磁轴处有最大值,并向外递减。
J-TEXT装置是一个圆形截面的托卡马克装置,根据平衡文件,大半经R=1.05 m,小半径a=0.35 m。VMEC程序利用一组傅里叶边界系数确定其边界[18]:
式中,RBC,ZBC,RBS,ZBS为傅里叶边界系数;m,n分别为极向模数和环向模数;u,v分别为极向角和环向角。
外部电流的设置适用于自由边界问题,本文讨论的固定边界问题,故将外部电流设置为固定值。
2.2 结果分析

图2(a)为三维磁场边界轮廓分布模型。从图2中可以看出,圆形截面,螺旋结构磁场位形,磁场强度由内向外(靠近和远离圆环中心)逐级递减。最大磁场约为2 T,磁轴磁场约为1.5 T,基本接近J-TEXT第1059184炮磁场大小。图2(b)是径向磁场BR在小截面上的分布。径向磁场BR是极向磁场Bθ的径向分量。从图中可以看出,BR关于Z=0轴对称,同时满足在Z=0时等于零。在极向方向0~2π,BR先反向增大后递减为零,再正向增大后减小为零。图2(d)是轴向磁场BZ在小截面上的分布。轴向磁场BZ是极向磁场Bθ的轴向分布,与径向磁场BR共同组成极向磁场。从图2中可以看出,BZ关于Z=0轴对称。在Z=0轴上,从大环内侧向大环外侧逐级递增。在极向方向0~2π,BZ先减小再增大。图2(c)是环向磁场Bφ在小截面上的分布。环向磁场的基本位形可由安培环路定律得到,它与大半经R呈反比。从图中可以看出,Bφ关于Z=0轴对称。在Z=0轴上,从大环内侧向大环外侧逐级递减,与J-TEXT第1059184炮实验数据基本吻合。在极向方向0~2π,BZ先增大再减小。

图2 基于J-TEXT第1 059 184炮平衡数据,三维磁场位形分布Fig.2 Based on the equilibrium data of J-TEXT No.1,059,184 gun, the three-dimensional magnetic configuration distribution
图3主要是径向磁场BR,轴向磁场BZ和环向磁场Bφ在小截面的分析。为分析磁场的环向分布,取磁面r=1(磁轴附近)和r=49(大环外侧边界附近),在极向角θ=0°,计算BR、BZ、Bφ随环向角φ的变化。
图3(a),3(b)是BR在极向角θ=0°,磁轴和边界的随环向角φ变化的图。从图中可以看出,BR在磁轴和边界处的变化规律相同,都是先递减再递增再递减。在φ=90°和φ=270°附近取得最值,并且φ=180°截面对称。图3(c),3(d)是Bφ在极向角θ=0°,磁轴和边界的随环向角φ变化的图。从图中可以看出,Bφ在磁轴和边界处的变化规律相同,都是先递增再递减。在φ=180°处取得最值,并且关于φ=180°截面对称。图3(e),(f)是BZ在极向角θ=0°,磁轴和边界的随环向角φ变化的图。从图3中可以看出,BZ在磁轴和边界处的变化规律相同,都是先递增再递减。在φ=180°处取得最值,并且φ=180°关于截面对称。
3 等离子体参数对三维磁场的影响
3.1 等离子体电流对三维磁场的影响
为分析等离子体电流对三维磁场的影响,选取等离子体电流Ip=-100 kA,Ip=-220 kA两种电流在压强剖面不变的情况下,分别计算径向磁场BR,轴向磁场BZ和环向磁场Bφ在环向位置φ=0°的小截面分布,如图4所示。
结合图2的小截面分布图,可以发现的极向方向,的径向方向磁场变化较为明显,而变化不明显。为更加清楚的比较,分解得到在和极向方向分布图(图5)以及在和径向分布图(图6)。
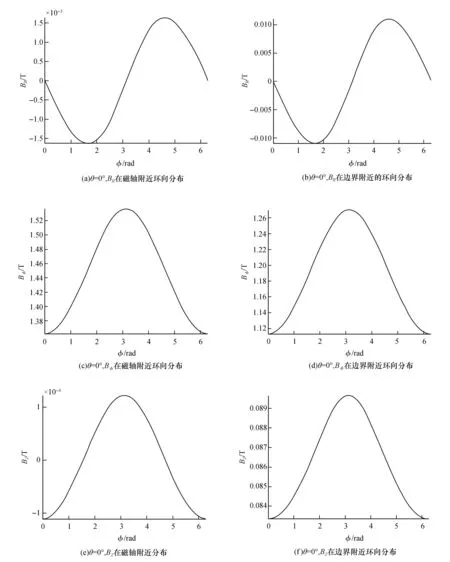
图3 极向角度为零时,BR、Bφ、BZ在磁轴和边界附近随环向角的变化图Fig.3 When the pole angle is zero, BR, Bφ and BZ near the magnetic axis and the boundary change with the ring angle

图4 不同等离子体电流下BR、Bφ、BZ小截面分布Fig.4 Distribution of small cross-sections of BR, Bφ and BZ under different plasma currents
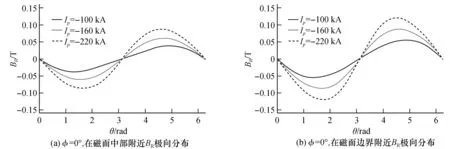
图5 环向角φ=0°,不同等离子体电流下BR在中部以及边界附近的极向分布;Fig.5 Circumferential angle φ=0°, the polar distribution of BR in the middle and near the boundary under different plasma currents
图5(a),(b)分别是BR在r=25(中间)附近以及在磁面r=49(边界),φ=0°,不同压强下的极向分布图。从图中可以看出,在磁面r=25(中心)附近以及在磁面r=49(边界)附近,Z轴上方,BR在Ip=-220 kA比Ip=-160 kA达到最值要慢,但是达到最值的值要大,而在Ip=-100 kA比Ip=-160 kA达到最值要快,但是最值的值较小。Z轴下方,BR在Ip=-220 kA比Ip=-160 kA达到最值要快,且达到最值的值也要大,而在Ip=-100 kA比Ip=-160 kA达到最值要慢,且最值的值也较小。由此可见,等离子电流越大,在等离子体中间靠边界处,BR的极向方向变化会变缓,但是数值会变大。

图6 环向角φ=0°时,在不同等离子体电流下BZ在极向角θ=0°及θ=180°的径向分布Fig.6 Circumferential angle φ=0°, the radial distribution of BZ at the polar angle θ=0° and the polar angle θ=180° under different plasma currents
图6(a),(b)分别是BZ在θ=0°以及θ=180°,φ=0°,不同等离子体电流下的径向分布图。从图中可以看出,在θ=0°附近,由中心向边界沿着径向方向,BZ在Ip=-220 kA比Ip=-160 kA递增地更高,而在Ip=-100 kA比Ip=-160 kA递增低一些。在θ=180°附近,由中心向边界沿着径向方向,BZ在Ip=-220 kA比Ip=-160 kA递减地更快,而在Ip=-100 kA比Ip=-160 kA递减慢一些。由此可见,在Z轴的左侧,等离子体电流越大,递增越大;在Z轴右侧,等离子体电流越大,递减越大。
等离子体电流产生极向磁场以及少部分的环向磁场。随着Ip增大,极向磁场分量BR,BZ也随之增大。BR在θ=0°附近极向方向变化缓慢,在θ=180°附近极向方向变化变快。BZ在磁轴左侧变化幅度变小,磁轴右侧变化幅度变大。而环向磁场Bφ基本保持不变。
3.2 等离子体压强对磁场的影响
为分析等离子体压强对三维磁场的影响,选取磁轴处的最大压强p0=2 100 Pa和p0=8 400 Pa两种压强,如图7(a)、7(b)所示。在等离子体电流Ip=-160 kA不变的情况下,分别计算径向磁场BR,轴向磁场BZ和环向磁场Bφ在环向位置φ=0°的小截面分布,如图8所示。
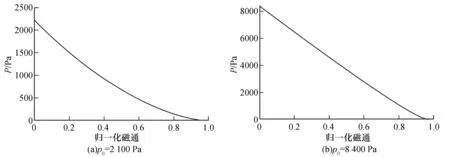
图7 两种不同的压强剖面图Fig.7 Two different pressure profiles

图8 不同等离子体压强下BR、Bφ、BZ小截面分布Fig.8 Distribution of small cross-sections of BR, Bφ and BZ under different plasma pressures
结合图2的小截面分布图,可以发现BR的极向方向,BZ的径向方向磁场变化较为明显,而Bφ变化不明显,但磁轴向大环外侧偏移。为更加清楚的比较,分解得到BR在r=25和r=49极向方向分布图(图9)以及BZ在θ=0°和θ=180°径向分布图(图10)。
图9(a)、图9(b)分别是BR在r=25(中间)附近以及在磁面r=49(边界),φ=0°,不同压强下的极向分布图。从图9可以看出,在磁面r=25(中心)附近以及在磁面r=49(边界)附近,Z轴上方,BR在p0=8 400 Pa比p0=4 200 Pa更快达到最值,而在p0=2 100 Pa比p0=4 200 Pa要慢一些到达。Z轴下方,BR在p0=8 400 Pa比p0=4 200 Pa要慢,p0=2 100 Pa比p0=4 200 Pa更快达到最值。由此可见,压强越大,在等离子体中间靠边界处,BR的极向方向变化更陡峭。

图9 环向角φ=0°,在不同等离子体压强下BR在中部以及边界附近的极向分布Fig.9 Circumferential angle φ=0°, the polar distribution of BR in the middle and near the boundary under different plasma pressures
图10(a),10(b)分别是BZ在θ=0°以及θ=180°,φ=0°,不同压强剖面下的径向分布图。从图中可以看出,在θ=0°附近,由中心向边界沿着径向方向,BZ在p0=8 400 Pa比p0=4 200 Pa递增地更高,而在p0=2 100 Pa比p0=4 200 Pa递增低一些。在θ=180°附近,由中心向边界沿着径向方向,BZ在p0=8 400 Pa比p0=4 200 Pa递减地更缓,而在p0=2 100 Pa比p0=4 200 Pa递减快一些。由此可见,在Z轴的左侧,压强越大,递增越大;在Z轴右侧,压强越小,递减越大。
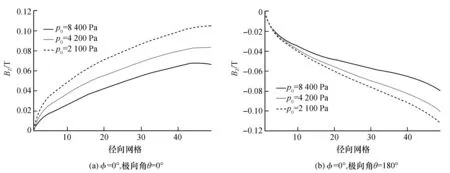
图10 环向角φ=0°,在不同等离子体压强下BZ在极向角θ=0°以及极向角θ=180°的径向分布Fig.10 Circumferential angle φ=0°, the radial distribution of BR at the polar angle θ=0° and the polar angle θ=180° under different plasma pressures
等离子体的一个重要参数β,它的定义为等离子体压强与磁场压强的当量比。随着p0增大,等离子体趋于环向膨胀,致使β值变大,磁轴外移。BR在极向方向稍微变化增大,但大致保持原来的形状。BZ在Z轴右侧径向方向变化更大,而Bφ磁轴向外偏移,其余基本保持原来形状。
4 结 论
本文运用VMEC程序,基于J-TXET装置第1059184炮平衡文件数据,对J-TXET装置等离子体平衡位形进行计算。计算得到的圆形截面,螺旋结构磁场位形,磁场强度由内向外(靠近和远离圆环中心)逐级递减。结果表明,得到的磁场位形以及磁场强度基本符合J-TEXT装置实验数据,故可以初步论证VMEC程序可以满足J-TEXT装置三维磁场平衡位形的计算。
本文进一步分析了等离子体电流和压强剖面对三维磁场的影响。等离子体电流直接影响极向磁场的强度,环向磁场影响不大。压强对三维磁场的强度影响甚小,当等离子体压强较大时,等离子体倾向于环状膨胀,而当等离子体压强降低时,等离子体则会环状收缩。本文只讨论了固定边界,外部电流恒定的情况,下一步的工作对于自由边界问题展开更深入的研究。
