粒子群优化模糊PID的塔式起重机定位和防摆研究

王 博, 肖金凤, 贾 磊, 张 宁

(1.南华大学 电气工程学院,湖南 衡阳 421001;2.深圳市海浦蒙特科技有限公司,广东 深圳 518000)

0 引 言

塔式起重机作为一种现代运输机械，广泛地应用在工程机械领域，并发挥着巨大作用。在运输过程中，由于会受到外界干扰以及操作人员工作经验的限制，造成小车定位不准确和负载大幅摆动等问题，影响运输效率，甚至造成安全事故。因此研究塔式起重机快速定位和消除摆动有很大的意义[1]。

近年来，国内外学者针对塔式起重机系统防摆控制问题进行了很多的研究工作，主要分为线性控制和非线性控制。马海峰团队采用变论域方法设计四输入单输出的双二维模糊控制器[2]；黄凯等人将模糊技术、神经网络技术和(linear quadratic regulator,LQR)最优控制方法相结合，应用到起重机防摆控制中，并加入自适应控制，提高了系统的鲁棒性[3]；孙艳芬通过模糊控制自适应方法调节(proportion integration differentiation,PID)参数[4]；游谊等人采用遗传算法优化PID参数，使得参数的收敛速度加速，提高控制效率和稳态精度，但是算法比较复杂[5]。

本文利用粒子群优化(particle swarm optimization，PSO)方法，以综合评判指标(integrated time absolute error,ITAE)作为PSO的适应度函数，对模糊PID控制器的量化因子Ke、Kec和比例因子Ku三个权重因子迭代计算，使得系统的权重因子可以快速整定，不仅减弱了模糊控制器对专家经验的依赖程度，也使得起重机控制系统快速达到稳态，实现控制器参数的智能调节。

1 塔式起重机数学模型的建立

塔式起重机系统非常复杂，具有强非线性的特点，在进行理论分析时需要忽略一些次要因素，从而建立理想的数学模型。根据文献[6]的假设，采用分析力学中的拉格朗日(lagrange)方程来建立塔式起重机防摆系统的数学模型[6]。

塔式起重机变幅运动简化模型如图1所示。

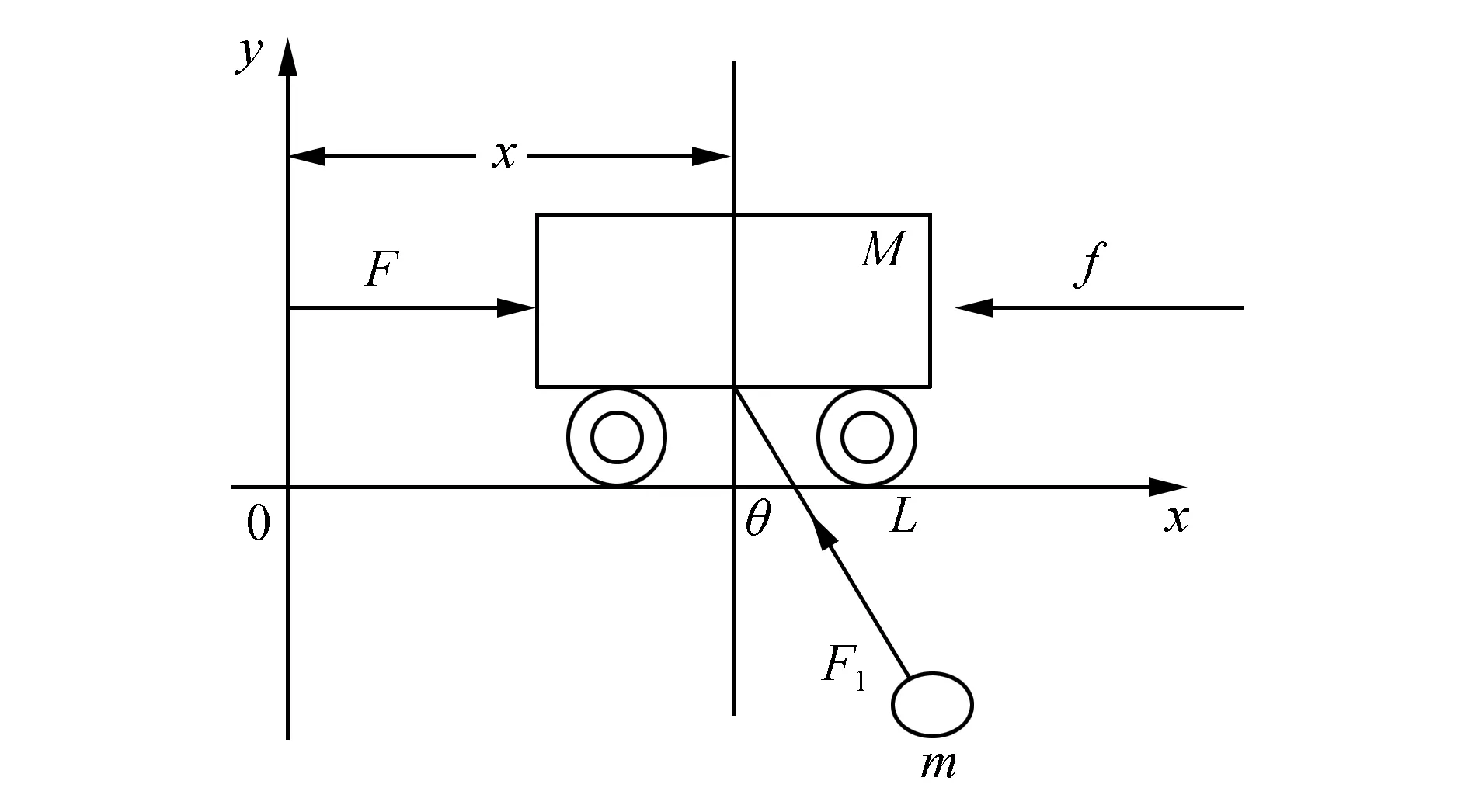
图1 塔式起重机变幅运动简化模型Fig.1 Simplified model of variable amplitude motion of tower crane

图1中，M为小车质量，m为负载质量，l为吊绳的绳长，F为小车的牵引力，F1为钢丝绳的拉力，f为小车与轨道的摩擦力，x为水平方向的位移，θ为负载与竖直方向的夹角即摆角。

利用拉格朗日方程对塔式起重机防摆系统进行受力分析可得：

(1)

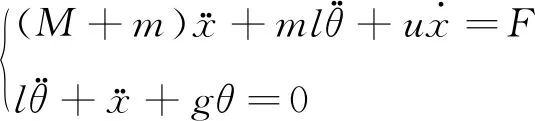
(2)

将式(2)进行拉普拉斯变换，得：

(3)

2 模糊PID控制

2.1 常规PID控制

比例积分微分控制器是一种线性控制器，其原理框图如图2所示。

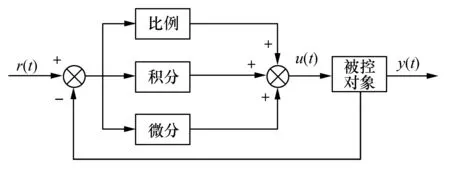
图2 PID控制原理框图Fig.2 PID control principle block diagram

其控制偏差由e(t)由给定值r(t)与实际输出值y(t)所构成：

e(t)=r(t)-y(t)

(4)

PID的控制器算法表达式为：

(5)

式中：Kp为比例系数；Ki为积分时间常数；Kd为微分时间常数。

针对塔式起重机控制系统是一个大时滞性、时变及非线性的控制系统，常规PID控制器由于存在参数不能在线调整问题，使得Kp、Ki、Kd三个参数难以整定，难以满足实际的控制需求。因此，本文采用模糊PID控制方法，来对PID的三个参数进在线调整，使其能够满足实际的控制需求。

2.2 模糊PID控制器设计

模糊PID控制是将模糊理论与PID控制结合起来[7]，其原理框图如图3所示。

图3 模糊PID原理框图Fig.3 Fuzzy PID principle block diagram

其中误差e和误差变化率ec作为模糊控制器的输入变量，经过量化因子Ke、Kec调整(模糊化过程)，调整为E、EC，输入到模糊控制器中。模糊控制器根据输入参数的隶属度函数，通过查表来确定相应的模糊量输出。最后再通过解模糊以及比例因子ΔKp、ΔKi、ΔKd的调整转化为实际输出，作用于PID控制器。

本文采用模糊PID控制设计了两个控制器分别对小车位移和负载摆动进行控制。根据实际情况，设定位置控制器，起重机位移偏差的论域为[-2,2],位移偏差变化率的论域为[-0.7,0.7],输出变量ΔKp、ΔKi、ΔKd的论域分别为[-6,6]，[-3,3]，[-6,6]。设定摆角控制器，摆角偏差的论域为[-1,1],摆角偏差变化率的论域为[-0.5,0.5],输出变量ΔKp、ΔKi、ΔKd的论域分别为[-6,6]，[-3,3]，[-6,6]。误差e、ec和ΔKp、ΔKi、ΔKd的模糊子集均由7个语言变量值组成，即为{负大，负中，负小，零，正小，正中，正大}，一般用英文缩写为{NB，NM，NS，ZO，PS，PM，PB}。考虑到分辨率以及数据的处理速度，将输入输出的隶属函数均选择trimf类型。根据以往的经验以及ΔKp、ΔKi、ΔKd对系统输出响应的影响得出模糊控制规则如表1、2、3所示。

表1 ΔKp控制规则表Table 1 ΔKp control rules table

表2 ΔKi控制规则表Table 2 ΔKi control rules table

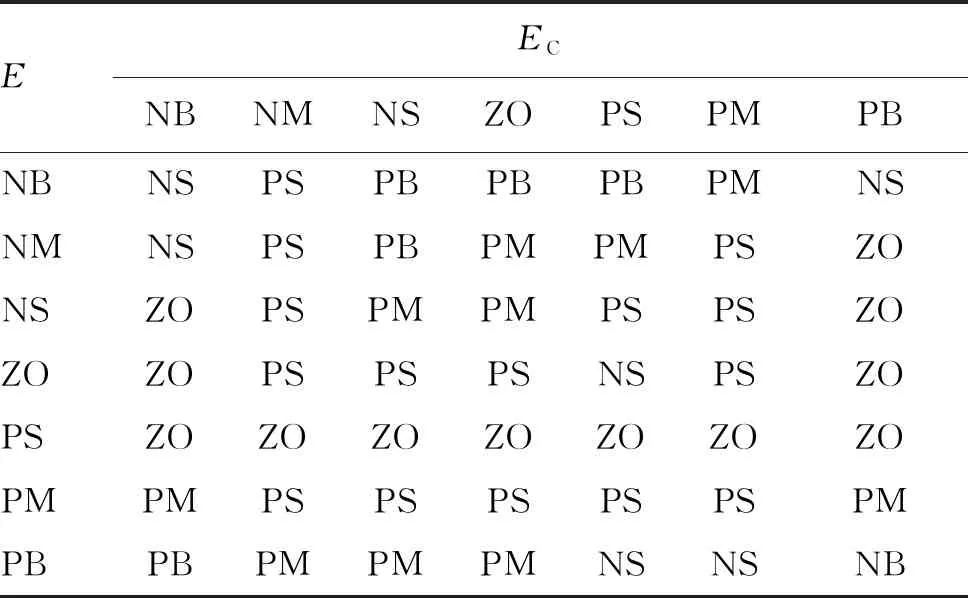
表3 ΔKd控制规则表Table 3 ΔKd control rules table

根据PID参数整定规则，得到自调整PID三个参数的修正公式：

Kp=Kp0+ΔKp

Ki=Ki0+ΔKi

Kd=Kd0+ΔKd

(6)

式中：Kp0、Ki0、Kd0为PID控制三个参数的初始值；ΔKp、ΔKi、ΔKd为三个参数的修正值，KP、Ki、Kd为PID控制三个参数的取值。

3 基于粒子群算法的模糊控制器参数优化

3.1 粒子群算法

粒子群优化算法(particle swarm optimization,缩写为PSO)，最早是由心理学博士Kennedy和计算机智能化博士Eberhart于1995年提出的，其源于对鸟群捕食的行为研究[8]。它是近年来发展起来的一种基于群体智能的优化算法，具有规则简单、搜索速度快等优点。

假设在一个N维空间区域中搜索，其中种群中每个粒子的位置可表示为xi=(xi1,xi2,…,xin),(i=1,2,…,n)，即优化问题的一个潜在解；其速度表示为vi=(vi1,vi2,…,vin),(i=1,2,…,n)。在每次迭代中，粒子可以通过个体极值和群体极值来更新自身的速度和位置，即

(7)

(8)

式中：w、k为惯性权重和当前迭代次数；c1、c2为非负常数，表示加速度常数；r1、r2为[0,1]区间内均匀分布的随机数；Pij为粒子i的个体最优位置；Pgj为整个粒子群全局最优位置，j=1,2,…,N。

3.2 粒子群优化模糊PID控制器参数

在模糊控制器中，制定准确有效的模糊规则是模糊控制器的核心，但是否能实现对被控对象的有效控制还需要合适的量化因子和比例因子，随着不确定因子的增多，对量化因子和比例因子的仅仅凭借人工经验，难以获得比较理想的动态响应效果。本文通过粒子群算法良好的全局寻优能力，根据控制性能指标来优化量化因子和比例因子，从而实现对模糊PID控制器的智能优化。

本文采用绝对误差积分准则(ITAE)作为寻优目标，采用ITAE指标可以保证系统的快速响应性、超调量、调节时间以及稳态误差等。其函数表达式为：

(9)

粒子群优化模糊PID控制流程图如图4所示[9]，其中Kp、Ki、Kd、Kp1、Ki1、Kd1为比例因子，Ke、Kec、Ke1、Kec1为量化因子。

图4 粒子群优化模糊PID控制流程图Fig.4 Flow chart of particle swarm optimizationfuzzy PID control

4 仿真实验与分析

塔式起重机模型参数：小车质量M=5 kg，负载质量m=10 kg，绳长l=2 m，摩擦系数u=0.2，重力加速度g=9.8 m/s2。粒子群优化模糊PID参数设置：惯性因子为0.6，加速时间常数都取2，粒子群规模为30，最大迭代次数为50，最小适应值为0.1，速度范围为[-0.6,0.6]，在运行PSO算法程序时，需要优化的参数个数为10个，分别为Ke、Kec、Kp、Ki、Kd、Ke1、Kec1、Kp1、Ki1、Kd1。

粒子群算法优化过程可分为三个部分，第一部分为在MATLAB中用m文件编写粒子群优化程序；第二部分为运用函数Sim撰写目标函数的程序代码实现粒子群优化程序与Simulink仿真模型的连接；第三部分为Simulink仿真模型，其仿真模型图如图5所示。目标函数的主要语句如下所示：

function[z]=PSO_FPID(x)

z=y_out(end,1);

图5 塔式起重机智能防摆模型Fig.5 Intelligent anti-pendulum model of tower crane

运行MATLAB粒子群优化程序后，得到此时位置控制器和摆角控制器的初始参数Kp0、Ki0、Kd0、误差和误差变化率的量化因子Ke、Kec分别约为7.513，3.207，7.660，0.537，0.331，0.004，6.679，14.948，1，1。

将上述参数代入到模糊PID控制器中，则系统中采用常规PID控制、未优化的模糊PID控制和本文提出的基于PSO优化后的模糊PID控制3种控制下的阶跃响应能力。阶跃信号位置响应及负载摆角变化仿真结果分别如图6和图7所示。

图6 阶跃信号位置响应Fig.6 Position response of step signal

图7 阶跃信号摆角响应Fig.7 Swing Angle Response of Step Signal

由图6可以看出，常规PID控制所取得控制效果最差，系统存在着16.15%的超调量，在第3 s时到达峰值，第10 s时系统进入稳态。而模糊PID控制时，系统的超调量下降至13.22%，控制效果得到了一定的改善，但还有待优化。经过PSO优化模糊PID控制后的系统，其超调量控制在0.5%左右，系统到达稳态的时间减少了一半，稳态误差也比较小。所以，经过PSO优化后的模糊PID在小车定位方面具有更好的控制效果。

由图7可以看出，在运行过程中负载会出现两次比较大的摆角。常规PID控制系统下摆角的最大值为0.126 1 rad,最小值为 0.070 5 rad；模糊PID控制系统下摆角的最大值为0.097 7 rad,最小值为0.058 9 rad；而PSO优化模糊PID的系统下摆角的最大值为0.067 2 rad,最小值为0.044 4 rad。PID控制和模糊PID控制的阶跃响应在3～9 s之间出现了两次明显的摆角震荡，而PSO优化后的模糊PID控制器在5 s之后就一直持续的衰减，防摆效果最佳。

5 结 论

针对常规PID控制器无法在线调整参数问题，采用模糊PID进行替代。进而提出了一种粒子群优化算法和模糊PID复合控制方法。在MATLAB中建立塔式起重机智能防摆模型，通过仿真分析，与常规PID控制和模糊PID控制的效果进行比较，发现PSO优化模糊PID仿真模型在保证小车准确定位的同时，还能有效的抑制负载的摆角，且具有较好的动态性能。