关于水母治理Filippov模型的动力学性质分析
2021-05-13王艺霖董秀辉
王艺霖,王 新,刘 兵,侯 祥,董秀辉
(1.辽宁师范大学 数学学院,辽宁 大连 116029;2.鞍山师范学院 数学与信息科学学院,辽宁 鞍山 114007;3.鞍山市气象局,辽宁 鞍山 114004)
水母是水生环境中重要的浮游生物,有着复杂的结构和生命史,是海洋生态系统中的一个重要物种.水母暴发是指水母在特定季节、特定海域内数量激增的现象.以往大约40年才有一次水母暴发,近年来越来越频繁.研究发现,水母数量超过一定水平,就会对旅游业、发电厂和核电站的正常工作造成影响[1];水母与鱼类争夺饵料也会使各大渔场获鱼量持续下降[2].为此,要对水母进行控制,把这种需要控制的危害水平称为经济阈值.
目前,中外学者针对水母暴发问题已做了一些研究,包括钵水母生活史的长期动力学行为、建立不同生命周期阶段受温度影响的过程模型,等等[3-4],但关于控制水母方面的研究成果却很少.本文利用具有切换策略的动力学模型模拟水母的控制过程,当水母数量未超过经济阈值时,不加干预;超过经济阈值时,再对水母进行捕捞,将水母数量控制在经济阈值内,为此建立Filippov水母控制模型.关于Filippov模型,在害虫治理[5]、植物疾病研究[6]、传染病研究[7]等多个方面已有广泛应用.本文得到的结果希望能为沿海生态和渔业、旅游业等发展提供相应的理论依据.
1 模型的建立和预备知识
1.1 模型的建立
假设水母种群是密度制约,而水螅体种群为非密度制约.水螅体通过自我复制和水母的有性繁殖补充,而水母只能通过水螅体的横裂补充.当水母种群数量小于经济阈值ET时,建立如下方程:
(1)
其中,x(t),y(t)分别表示t时刻水螅体和水母的数量,a为实数,b,c,d,b2为非负实数.a表示水螅体的自我复制率与死亡率的差,假设a始终小于0;b表示水母有性繁殖成水螅体的存活率;c为水螅体无性繁殖成水母的存活率;d为水母的死亡率;b2为水母种内竞争率.
当水母种群数量大于ET时,按比例δ(为非负实数)打捞水母,此时方程为
(2)
系统(1)、(2)等价于
(3)
其中,
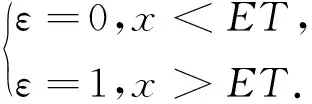
1.2 Filippov系统预备知识
令
H(Z)=y(t)-ET,
其中,
Z=(x,y)T,
且
FI1(Z)=(ax+by,cx-dy-b2y2)T,
FI2(Z)=(ax+by,cx-dy-b2y2-δy)T,
那么系统(1)和系统(2)合写为Filippov系统
(4)
其中,
另外,记
为分割两个区域I1和I2的分界线.
定义1令
Σs={Z∈Σ|〈HZ,FI1(Z)〉〈HZ,FI2(Z)〉<0},
称Σs为滑线区域,其中〈·〉表示内积,H(Z)是一个光滑的纯量函数,在Σ上关于H(Z)的梯度为
HZ=(0,1).
引理1(Filippov凸理论)如果滑线是光滑的,滑线系统可以表示为
其中,
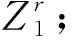
(ii) 如果系统(4)的滑线区域Σs的平衡点Z1满足
λFI1(Z1)+(1-λ)FI2(Z1)=0,0<λ<1,
则称Z1为系统(4)的伪平衡点.
2 子系统动力学
2.1 系统(1)的动力学性质
系统(1)始终存在灭绝平衡点A0(0,0),当ad+bc>0时,存在正平衡点A1(x1,y1),其中,
定理1对于系统(1),当ad+bc<0时,正平衡点不存在,A0为全局渐近稳定的;当ad+bc>0时,A0为鞍点,系统(1)存在唯一的正平衡点A1,且它是全局渐近稳定的.
证明系统(1)在平衡点A(x,y)处的Jacobian行列式为
Tr(J(A0))=a-d,Det(J(A0))=-(ad+bc).
当
ad+bc<0
时,容易看出
Tr(J(A0))<0,Det(J(A0))>0,
此时A0为局部渐近稳定的.
当
ad+bc>0
时,显然此时A0为鞍点;此时存在唯一正平衡点A1,
Det(J(A1))=ad+bc.
可以得出
Tr(J(A1))<0,Det(J(A1))>0,
此时A1为局部渐近稳定的.又知不存在极限环,因此A1为全局渐近稳定的.
2.2 系统(2)的动力学性质
类似系统(1)的分析,显然系统(2)始终存在灭绝平衡点B0(0,0),当
ad+bc+aδ>0
时,存在正平衡点B1(x2,y2),其中,
类似于定理1的证明,可得如下结论:
定理2对于系统(2),当ad+bc+aδ<0时,正平衡点不存在,B0为全局渐近稳定的;当ad+bc+aδ>0时,系统(2)存在唯一的正平衡点B1,且它是全局渐近稳定的.
3 滑动模态及平衡点
由定义1知,滑面Σs存在条件为F2>0,F4<0,得
Σs={(x,y)|y=ET,x′≤x≤x″},
其中,
由引理1,滑面上的动力系统为
当
时,滑面存在唯一伪平衡点
容易看出该条件等价于
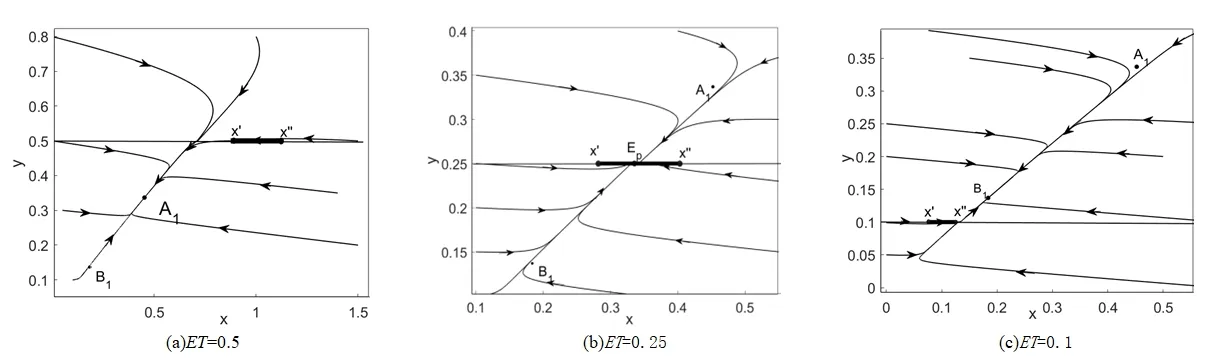
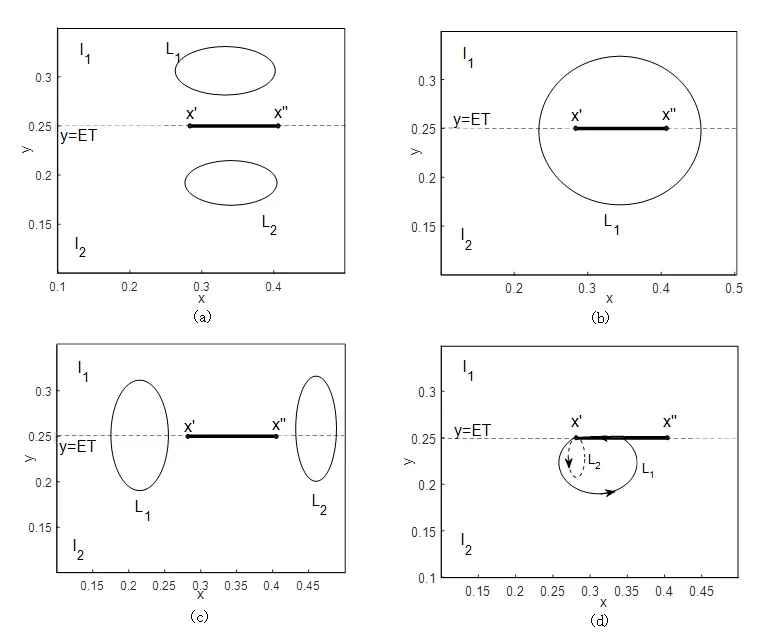
y2 令 F(x)=ax+bET,F′(xEp)=a<0, 故伪平衡点存在时,为局部渐近稳定的. 类似于文献[7],有如下结论: 定理3Filippov系统(4)中不存在以下几种极限环: (1)包含于区域Ii(i=1,2)内部的极限环(如图1(a)所示); (2)环绕滑线的穿越极限环(如图1(b)所示); (3)不环绕滑线的穿越极限环(如图1(c)所示); (4)鸭型环(如图1(d)所示). 图1为Filippov系统(4)用以表示吸引域内各种可能的不同类型极限环的相图,x′x″表示滑线,细虚线表示横截区域,Li(i=1,2)表示可能的极限环. 令 A1=(x1,y1),B1=(x2,y2), 根据正平衡点A1、B1,显然有y2 由以上分析,可以得到: 图1 各极限环相图 本文基于水螅体和水母的关系建立了一个Filippov水母控制模型,通过理论推理发现ET取值不同,对应的动力学性质也不同.由定理4可知: (1)当y2 (2)当y2 (3)当y1>y2>ET时,B1为真平衡点且全局渐近稳定,此时水母数量超过经济阈值,对生态造成危害,不是想要的结果,在实际捕捞水母中,要尽量避免这种情况发生(见图2(c)). 图2 平衡点稳定性相图 a=-0.298,b=0.4,c=0.02,d=0.01,b2=0.05,δ=0.01.4 全局动力学
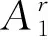
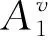
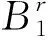
5 结论