基于K-means算法的QRS波群检测研究

余 顺，张 平，王 曾

（安徽职业技术学院 信息工程学院，安徽 合肥 230011）

心电图（Electrocardiograph，ECG）是一种由电子设备所检测出来的微弱的电信号，一个完整的ECG 信号应该包含一个P波、一个QRS波群、一个T 波和一个U 波，其中QRS 波群集聚了ECG 信号中的主要的能量，同时也包含了ECG 信号的重要特征信息，因此QRS 波群检测也是ECG 信号特征识别的重要部分。

QRS 波群包含三个部分子波，分别是Q 波、R波和S 波，其中R 波以其高振幅和高频率等特性成为了ECG信号特征识别的关键。

针对ECG 信号的检测研究，目前主要有包志强、罗小宏等人提出的自适应CA-CFAR 的心电信号R 波检测技术，这种方法将ECG 信号中R波检测的精准率提高到了99.842%。隋文涛、崔善政等人提出的基于变分模态分解的心电信号QRS 波检测，该方法可以准确的检测和定位QRS 波群。王海英、王远远等人提出的基于变分模态分解的心电信号QRS 波检测算法，此方法的QRS波群检测准确率达99%以上。

本文在研究QRS 波群检测定位时，在原有的基于差分绝对值极值算法的基础上，引入k 均值聚类的思想。在QRS 波群检测前，对ECG 信号利用K-means 算法进行分类，利用R 波的高振幅特性，将R波范围缩小，再在此范围利用差分绝对值极值算法对QRS 波群进行检测。本文采用定量的方法对利用埃德仪器国际贸易有限公司所生产的人体生理信号无线遥测系统所测得5 组数据和MIT-BIH数据库中的5组数据进行实验。

1 ECG信号预处理

ECG 信号在采集和处理过程中会产生一些干扰的电信号我们称为噪声。噪声会影响ECG信号的分类和检测，为了能够在后期对ECG 信号进行分类和检测过程中获得更加精确的检测结果，我们需要先对ECG 信号进行去除噪声预处理。

由于本文所选用的由埃德仪器国际贸易有限公司所生产的人体生理信号无线遥测系统所测得5 组ECG 信号和MIT-BIH 数据库中的5 组ECG 信号都是经过处理后的数据，为了能够真实的反应噪声对ECG 信号的影响以及去除噪声的必要性。我们先对ECG 信号进行人工添加噪声，然后再利用小波变换对添加了噪声的ECG 信号进行去除噪声预处理。

首先，读取ECG 信号；其次，将噪声信号加入ECG 信号中，我们添加了肌电干扰和基线漂移两种干扰噪声。最后，利用小波变化对添加了噪声的ECG 信号进行去除噪声预处理。具体结果如图1所示。

图1 ECG信号去除噪声预处理

2 K-means算法

基本原理：给定一个数据集合A={a，a，a……a}，第一，选取K个对象作为K-means算法的原始聚类中心。第二，计算每一个点与各个聚类中心的距离，根据就近原则，把每个点归入最近的类中。第三，根据分类结果，重新计算各个类的中心点。第四，反复执行第二和第三两个步骤，直至满足收敛条件才结束。

利用K-means 算法对ECG 信号进行分类实验，初步选取K=4，利用matlab 软件对利用埃德仪器国际贸易有限公司所生产的人体生理信号无线遥测系统所测得5组数据和MIT-BIH 数据库中的5组数据实验。

首先，读取经过去除噪声预处理后的ECG 信号；其次，对ECG 信号进行K-means 聚类计算，如图2 所示；最后，根据K-means 算法的分类结果，初步提取出ECG 信号中R 波的大致区域范围，如图3所示。

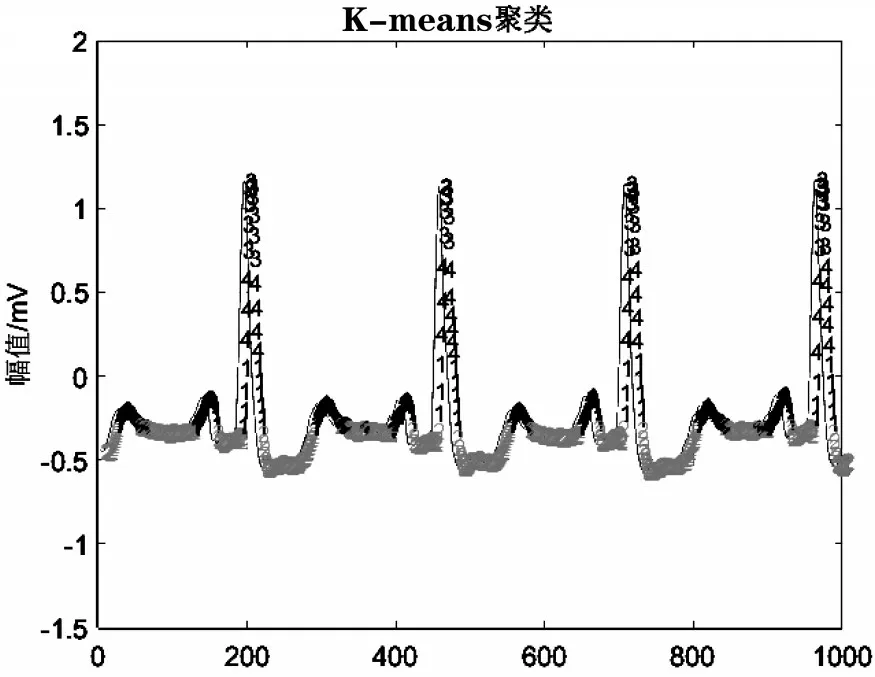
图2 K-means聚类算法分类

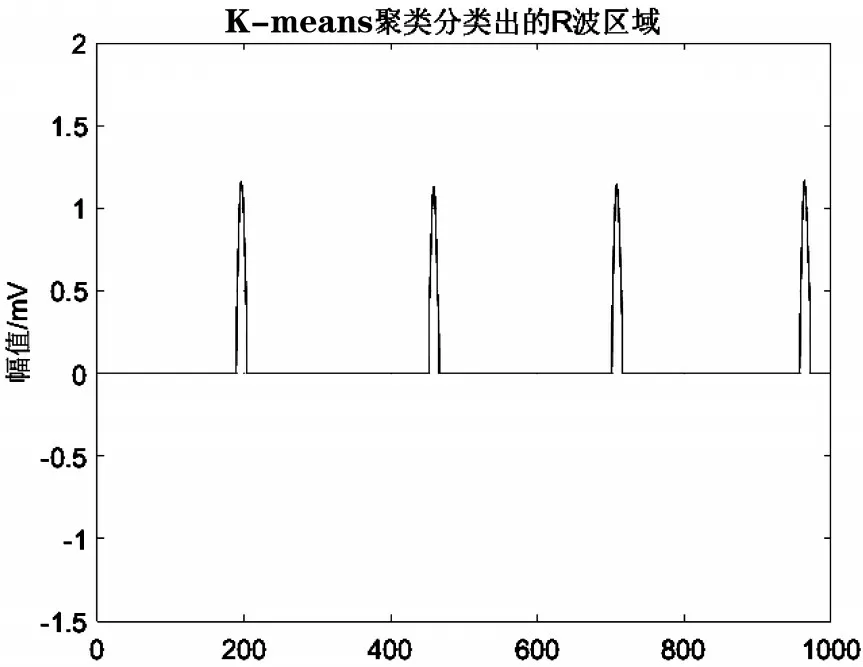
图3 R波分类结果

利用K-means 聚类算法对ECG 信号进行分类，R 波的区域范围记作［a b］，为后期的ECG 信号特征识别做基础。

3 基于差分绝对值极值算法

3.1 差分绝对值极值算法的基本原理

根据R波的高振幅、高斜率的特性，采用求极限的方法，找出该区域的极值点，再根据极值点找到相应的R 波峰值点位置。找出R 波位置后，再向R 波两侧利用求极限的方法找出极值点，进而找出Q波和S波的峰谷点。

3.2 算法流程

差分绝对值极值算法的算法流程基本可以分为以下3步：

（1）R波的检测

为了能够保证R 波采样运算的充分性，我们选取采样频率为：360HZ。令R 波为（fx），在经过K-means 算法确定出的R 波区域［a b］内，对R 波f(x)进行一阶求导运算，具体运算公式为：

在数值运算中通常使用差分运算来代替微分运算，因此R波的一阶求导可以表示为式（1）。根据极限思想，首先，令＇f（x）=0。其次，在区域［a b］内进行求导运算，寻找该区域内所有的驻点。最后，寻找（fx）≠0 的驻点，则该驻点为极值点，用c［i］，i∈N∩i≥1 表示。利用R 波高斜率的特性，我们再求出各个极值点附近的斜率的绝对值，即求出c［i］+Δx处斜率绝对值｜＇f（c［i］+Δx）｜和c［i］-Δx 处斜率的绝对值｜＇f（c［i］-Δx）｜，并求出各个极值点附近斜率绝对值的平均值：

式（2）中Φ（c［i］）表示极值点c［i］附近的斜率绝对值的平均值。得到Φ（c［i］）后，再对各个c［i］处的Φ（c［i］）值进行比较，确定其中最大值的位置，该位置就是R波波峰（谷）所在的位置，并记录此处为c。

（2）Q波、S波检测

在确定了R 波波峰（谷）位置后，将c点映射到ECG 信号中相应位置并记为c'，再以c'点为起点，令ECG 信号为d（x），对ECG 信号分别向两边搜索，对ECG信号进行一阶求导运算，

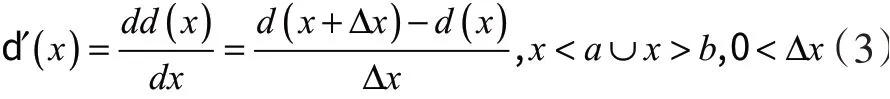
利用式（3）找出c'点两边的极值点记为c（j），再对得到的极值点附近斜率取平均值。

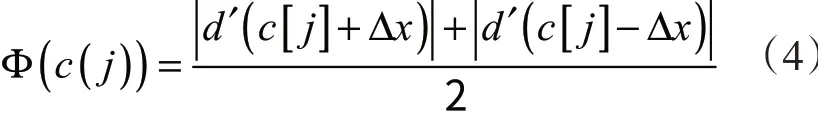
通过式（4）进而确定c'点左侧的极值点是Q波峰谷点的位置，记为c，c'点右侧的极值点就是S波峰谷点的位置，记为c。

根据以上结果，可以确定出QRS 波群的峰谷点位置，接着分别以c点和c点为起点，分别向左和向右搜寻ECG 信号（fx）的基线值点，左边基线位置为QRS 波群的起始点，记为c；右边的基线位置为QRS 波群的终点，记为c。这样整个QRS 波群的峰谷点、起点及终点就初步定位完成了。

（3）采用阈值法进行删误补漏

在对QRS 波群进行检测过程中，可能存在误检和漏检的情况。因此我们需要对ECG 信号进行删误补漏操作。利用ECG 信号中的一个非常重要的特征信息——RR 间期作为删误补漏的判定指标。RR 间期指的是相邻两个QRS 波群中两个R波波峰（谷）的间隔时间。

具体思想如下：

对所有检测出的QRS 波群的RR 间期进行求平均值运算，平均值记为s，对所有检测出的QRS波群的RR 间期进行判断，如果相邻两个QRS 波群的RR间期小于0.5s，则判定这两个QRS波群中存在误检情况，删除其中振幅较小的QRS 波群，并去除相应的标记点；若相邻两个QRS 波群的RR 间期大于1.66s，则认为这两个QRS 波群间存在漏检情况，将阈值改为0.6m，对该区利用K-means 算法和差分绝对值极值算法进行处理，以查找出漏检的QRS波群。

3.3 实验及数据

为了验证上述所提出的QRS 波群检测思路在QRS 波群检测中的效果，我们选用埃德仪器国际贸易有限公司所生产的人体生理信号无线遥测系统所测得的5 组心电数据和美国麻省理工学院的MIT-BIH数据库中的5组数据进行实验。

将K-means算法和差分绝对值极值算法相结合，对ECG 信号中的QRS 波群进行检测，得到了良好的检测效果。具体结果如表1和表2所示：

表1 人体生理信号无线遥测系统所测得的5组心电数据QRS波群检测结果

表2 MIT-BIH数据库中的5组数据心电数据QRS波群检测结果

4 结语

由表1和表2可以看出，针对利用埃德仪器国际贸易有限公司所生产的人体生理信号无线遥测系统所测得的1500 个ECG 信号心拍和美国麻省理工学院的MIT-BIH 数据库中的10897 个ECG信号心拍，先用K-means算法分类出R波区域，再利用差分绝对值极值算法进行精确的QRS 波群检测，分别可以正确检测出其中的1494 个心拍和10858 个心拍，综合检测准确率达到了99.64%。这对于QRS 波群检测来说是相当高的检测准确率。同时，本文所提出的算法是在原有的差分绝对值极值算法的基础上进行改进优化，本算法的算法复杂度和时间复杂度都比较低，在现实QRS波群的实时检测中具有一定的实际意义。