含新能源接入的配电网中分布式储能系统控制策略

董新伟，裴晨晨，邓薇，李滨，戴晖

(1.中国矿业大学电气与动力工程学院，江苏省徐州市 221116；2.国网湖北省电力有限公司 武汉供电分公司，武汉市 430077；3.国网江苏省电力有限公司丰县供电分公司，江苏省徐州市 221700；4.国网江苏省电力有限公司淮安供电分公司，江苏省淮安市 223001)

0 引 言

风电、光伏等间歇性新能源的规模化并网，使得大量电力电子设备投入使用，导致了谐波污染、电压波动等一系列问题，对配网的运行控制带来了极大影响[1-4]。为解决因新能源并网造成的电压波动问题，目前常采用可投切电容器、有载调压变压器、储能系统或是其他柔性设备进行调压，而分布式储能系统(distributed energy storage system，DESS)因其响应速度快，可双向调节，能提高新能源消纳能力等优势，得到了广泛应用[5-7]。

针对配电网的不同运行要求，提出相适应的控制策略，是充分发挥DESS调节作用的关键。为实现含新能源并入的配电网的安全稳定运行，现已有大量文献对DESS的控制策略进行了研究。文献[8]提出两段式电压协调控制策略，第一阶段以传统调压设备为控制对象，网损最小为目标函数建立优化模型，第二阶段基于电压灵敏度对DESS的有功-无功输出进行控制。文献[9]将控制过程划分为不同时间尺度执行，通过对光伏有功-无功出力的协调控制来保证配电网的安全稳定运行。文献[10]在考虑配电网运行控制策略的基础上，提出了储能系统的双层优化配置策略，以提高配电网对新能源的消纳能力。上述文献都采用了分层分段式的控制方式，但是没有将储能电站群的控制、配网的电压稳定与经济运行相结合。文献[11-12]都提出了储能系统充放电控制策略，来平抑光伏带来的功率波动，维持配电网的电压稳定，但没有考虑储能系统的无功调节与新能源的利用率。文献[13-15]针对新能源并网后带来的配电网电压稳定问题，提出改善方案，但没有结合DESS提出相应的控制策略。

综上所述，本文提出分时间尺度执行的DESS双层控制策略，以提高配电网电压稳定性及运行经济性。双层控制的上层为稳定控制层，确定各节点满足电压安全运行条件且电压偏差最小时储能系统总有功/无功功率，下层为优化控制层，对上层结果进行优化分配，利用粒子群算法(particle swarm optimization，PSO)求解配电网经济性最优、新能源利用率最高时各储能单元的功率。最后通过IEEE 33节点系统对所提出的控制方式进行验证。

1 基于双层控制提高配电网稳定性的控制策略

1.1 基于多时间尺度的双层控制

本文提出的控制策略为内外环嵌套控制，外环以时间为尺度纵向执行，执行结果限制内环的运行结果；内环由单层控制与双层控制方式组成，分时间尺度横向选择执行上层或双层控制，为外环提供反馈及运行结果参考量，其中上层控制可作为电压是否安全运行的判断控制层单独运行。具体执行过程如图1所示。

图1 多时间尺度的双层控制过程框架图

所谓双层包含稳定控制层和优化控制层，在输入新能源、储能电站、负荷等初始状态信息后，稳定控制层在满足电压安全运行的基础上以电压偏差值最小为目标函数，确定储能电站群总的有功/无功出力，作为优化控制层的输入参考值；优化控制层则实现配电网整体的经济运行，以配电网运行时网络损耗最小、新能源利用率最高为经济目标，对上层运行结果进行功率分配，确定各储能电站功率解集，其中有功网络损耗率、新能源损耗率为相对应的2项经济指标参与运算。

执行时间尺度分为时间间隔为ΔT的长时间尺度与时间间隔为Δt的短时间尺度，长时间尺度执行双层控制，执行结果上传至储能检测控制模块；短时间尺度首先执行稳定控制层，当发生电压越限时，立即执行双层控制，确定此时各储能单元的最优功率分配，并上传至储能检测控制模块，修正长时间尺度的运行结果。由于运行时是向储能电站下发此时刻的运行指令，长时间尺度运行结果是对ΔT时间内储能功率分配的预测值，短时间尺度运行结果最终决定这一时刻的功率分配。开始时刻以长时间尺度功率分配结果作为模块参考值，Δt后短时间尺度开始运行。

储能检测控制模块在未发生电压越限情况下，以长时间尺度的执行结果为参考值，根据DESS上传的实时状态信息，确定储能单元的工作模式及功率分配。当出现电压越限时，控制各储能单元首先进行无功调节，若是电压波动改善不明显，再通过储能有功功率进行协调控制。

1.2 储能电站的工作模式

储能检测控制模块设有5种工作模式，分别是充电模式、放电模式、充电速率减缓模式、放电速率减缓模式、正常模式。储能检测控制模块会根据各储能电站当前时刻的运行状态及剩余容量状态，确定下一时刻的充放电功率及运行模式，并向各储能电站的能量管理系统下发调度指令。各工作模式具体执行过程如下：

(1)

式中：SOCnow、SOCmax、SOCmin分别为储能电站此时刻的荷电状态值大小、荷电状态最大值及荷电状态最小值。

(2)

2 双层控制模型

2.1 稳定控制层模型

稳定控制层以储能电站群的有功/无功功率总量为优化目标，根据新能源出力以及负荷状态，得出节点电压偏差值最小时的目标值。

2.1.1稳定控制层目标函数

1)节点电压偏差值可表示为：

(3)

式中：Vm_tr为节点m电压的真实值；VN为额定电压；Y为配电网系统节点个数。

2)电压偏差判断矩阵Nju：

(4)

式中：ΔUm_flu(m=1,2,…,Y)表示节点m电压越限情况，当|Vm_tr-VN|>δVN时，ΔUm_flu=1,当|Vm_tr-VN|≤δVN时，ΔUm_flu=0，δ为允许电压偏离额定值百分比。

2.1.2约束条件

1)储能电站一般通过逆变器并网，而逆变器可向配电网提供一定的无功支撑，储能电站无功功率Qj_bess满足如下约束条件：

(5)

2)储能电站充放电功率及荷电状态SOC需满足如下控制条件：

Pjmin_ch≤Pj_ch≤Pjmax_ch

(6)

Pjmin_dis≤Pj_dis≤Pjmax_dis

(7)

SOCj_min≤SOCj≤SOCj_max

(8)

式中：Pjmin_ch、Pjmax_ch为储能电站j充电功率最小值、最大值；Pjmin_dis、Pjmax_dis为储能电站j放电功率最小值、最大值；Pj_ch、Pj_dis为储能电站j充、放电功率；SOCj_min、SOCj_max为储能电站jSOC最小值、最大值；SOCj为储能电站j的荷电状态。

3)储能电站i时刻的荷电状态与i+1时刻的荷电状态需满足以下条件：

(9)

式中：Ej_bess指储能电站j的额定容量；ηch、ηdis分别指充、放电效率；ρ为储能电站的自放电率；Δi为i与i+1间的时间间隔。

4)系统中各节点功率平衡约束：

Pm+Pm_new+rPm_bess-Pm_load=Um·

(10)

Qm+Qm_new+rQm_bess-Qm_load=Um·

(11)

式中：Pm_new、Qm_new为节点m新能源注入的有功、无功功率；Pm_bess、Qm_bess为节点m储能系统注入的有功、无功功率；Pm、Qm分别为节点m其他方式注入的有功、无功功率；Um、Un为节点m、n的电压；θmn为节点m、n间的相角差；Gmn、Bmn分别为节点导纳矩阵m行n列的实部和虚部；储能系统充电时为负荷，储能系统放电时为电源，r的具体数值如下：

(12)

5)储能电站j在i时刻的容量满足如下控制条件：

(13)

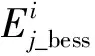
2.2 优化控制层模型

优化控制层将上层运行结果储能电站群的功率总量作为初始条件，求解配电网经济性最优、新能源利用率最高时各储能单元的有功/无功功率。配电网经济性最优即有功网络损耗率最小，新能源利用率最高即新能源损耗率最低，以此为目标函数进行优化求解。

1)有功网络损耗率ploss最小：

(14)

式中：N为储能电站的个数。

2)新能源损耗率wm_new最小：

(15)

3)多目标优化函数F：

F=ω1ploss+ω2wm_new

(16)

式中：ω1、ω2为惯性权重，惯性权重的确定采用德尔菲法，通过反复匿名征求及统计专家意见，由专家根据经验对各指标的重要性及权重进行评定[17]，确定有功网络损耗率和新能源损耗率的权重系数。

3 粒子群双层控制算法求解流程

PSO双层优化算法求解流程如图2所示，具体如下：

图2 PSO双层控制算法求解流程

1)输入初始条件，判断节点电压是否越限；

2)若节点电压出现越限，执行上层计算，储能电站群总有功/无功功率为求解的粒子值，遍寻满足电压在0.95～1.05 pu粒子中电压偏差最小的粒子值，作为下层优化参考值；

3)下层运算将多目标优化函数F作为适应度函数对上层运行结果进行优化分配，求解出各储能电站的功率解集；

4)判断储能电站只进行无功调节时，各节点电压是否能在安全范围内运行，若可以，输出各储能电站无功调节量，反之则输出有功、无功调节量，返回步骤1)，等待下一时刻执行命令；

5)若电压未越限，不进行无功优化，执行步骤2)、步骤3)中的上下层功率分配计算程序，输出各储能电站的充放电功率，返回步骤1)，等待下一时刻执行命令。

4 算例分析

4.1 算例仿真系统

本文以改进的IEEE 33节点系统为例进行算例仿真验证，系统拓扑如图3所示。基准电压为12.66 kV，节点电压允许范围为0.95～1.05 pu，在节点6、节点25接入光伏发电系统，额定功率为300 kW；节点11接入风能发电系统，额定功率为400 kW；为了能充分体现储能电站对系统电压波动可作出即时反馈的优势，在新能源并网附近电压易波动的关键节点7、12、26分别接入容量为600 kW·h的储能系统，最大充放电功率为300 kW，自放电率为0.05，充放电效率为0.95。通常系统中会接入其他无功补偿设备，以保证系统整体电压水平波动在可控范围内，本系统在节点27、31分别接入4组单组额定容量为60 kV·A的可投切电容器。

图3 IEEE 33节点仿真系统图

本文提出的控制方式中长时间尺度运行时间间隔为1 h，运行结果作为储能检测控制系统下发调度指令的参考值；短时间尺度运行时间间隔为15 min，首先运行电压稳定控制层，检测系统中的电压状态，电压正常状态下，不改变长时间尺度运行结果，若检测出电压越限，需更新储能检测控制模块指令参考值，对各储能系统的有功/无功功率重新分配。

4.2 仿真结果分析

新能源并网节点由于其并网功率的不确定性，节点电压波动比较剧烈，因此，选取节点6、11、25处的电压进行对比讨论，结果如图4—6所示。由图4可以看出，储能电站未参与调节时，节点6在01:00、19:00—20:00、21:00—24:00，节点11、25在18:00—24:00电压均低于0.95 pu，此时光伏出力为0，且在19:00—22:00负荷用电量较大，易导致电压不足的情况发生，影响用户用电质量。当储能电站仅进行充放电的有功调节时，虽在一定程度上可以提高电压水平，但01:00、18:00—19:00、24:00仍出现电压低于0.95 pu的情况，且电压波动幅度和波动频率改善不明显。当储能电站采用本文提出的控制策略，有功无功协调控制时，电压在各个时刻都在0.95～1.05 pu范围内，且电压波动幅度及波动频率在相同节点不同调节措施中都是最小的。

图4 储能参与前后节点6电压变化对比

图5 储能参与前后节点11电压变化对比

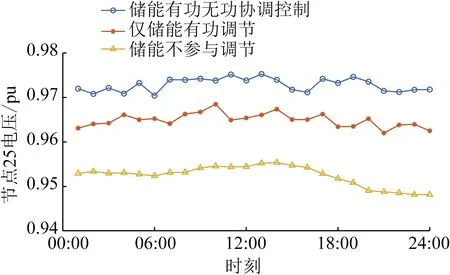
图6 储能参与前后节点25电压变化对比

从节点6、11、25电压的波动曲线可以看出，在18:00—22:00间易出现电压不足的情况，因此主要列出此期间储能电站的有功无功出力情况，结果如图7—10所示。以节点6为例，如图7所示，18:00时节点电压越限，储能电站此时发出无功功率进行调节，电压控制在安全范围内，15 min后短时间尺度运行的稳定控制层发现电压仍有越限行为，继续完成双层控制，重新进行功率分配，并将结果上传至储能检测控制模块，更新储能电站功率调度参考值，继续下达储能电站发出无功的指令，电压水平提升至安全范围内，18:30、18:45继续采用储能电站无功调节，19:00时通过计算判断电压正常，储能检测控制模块根据更新的有功分配结果及储能SOC下发调度指令。在短时间尺度下运算时，电压出现越限行为更新长时间尺度执行结果。

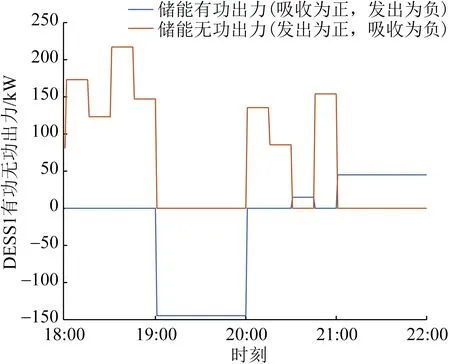
图7 DESS1有功无功出力

图8 DESS2有功无功出力

图9 DESS3有功无功出力

图10为各储能电站未采用所提控制方式，以15 min为其动作时间尺度时的充放电功率。由图10可看出，各储能电站充放电次数较采用多时间尺度双层控制方式频繁，易满充满放，对储能电站的使用寿命产生不利影响，且不能充分发挥其作用。

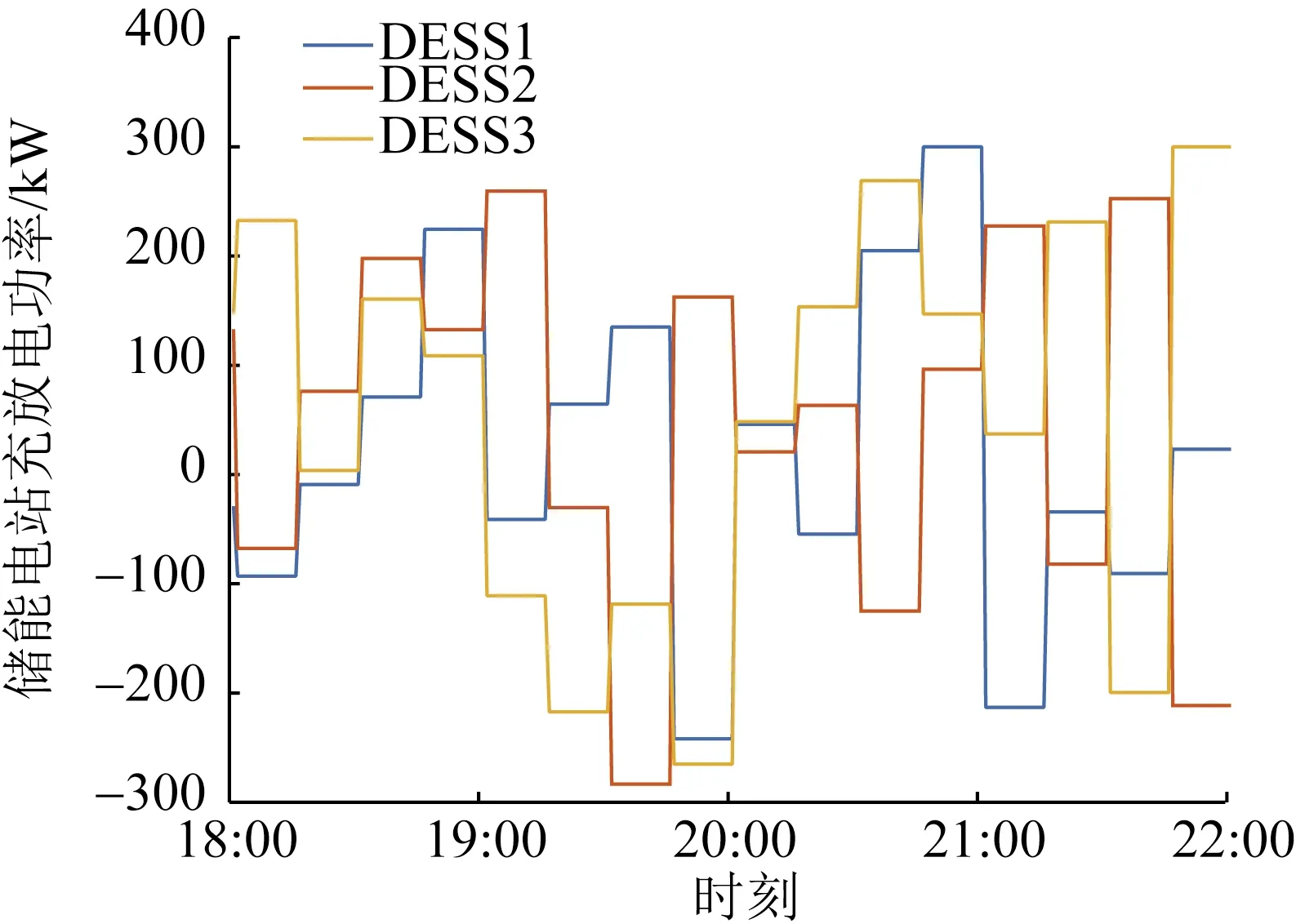
图10 储能电站充放电功率

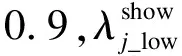
表1 各储能电站的工作模式

本文提出的双层控制方式，可提高配电网的运行经济性，结果如图11、12所示。储能电站采用所提控制方式参与调控后，有功网络损耗率ploss得到有效降低，其值基本位于2.5%～4%之间(而未采用本文控制方式时则大多位于4%～5%之间，或超过5%)，提高了系统有功的有效利用率。储能电站参与调节相较于未配置储能时，有功网损得到大幅度降低，有效减少了因网损引起的经济损失。

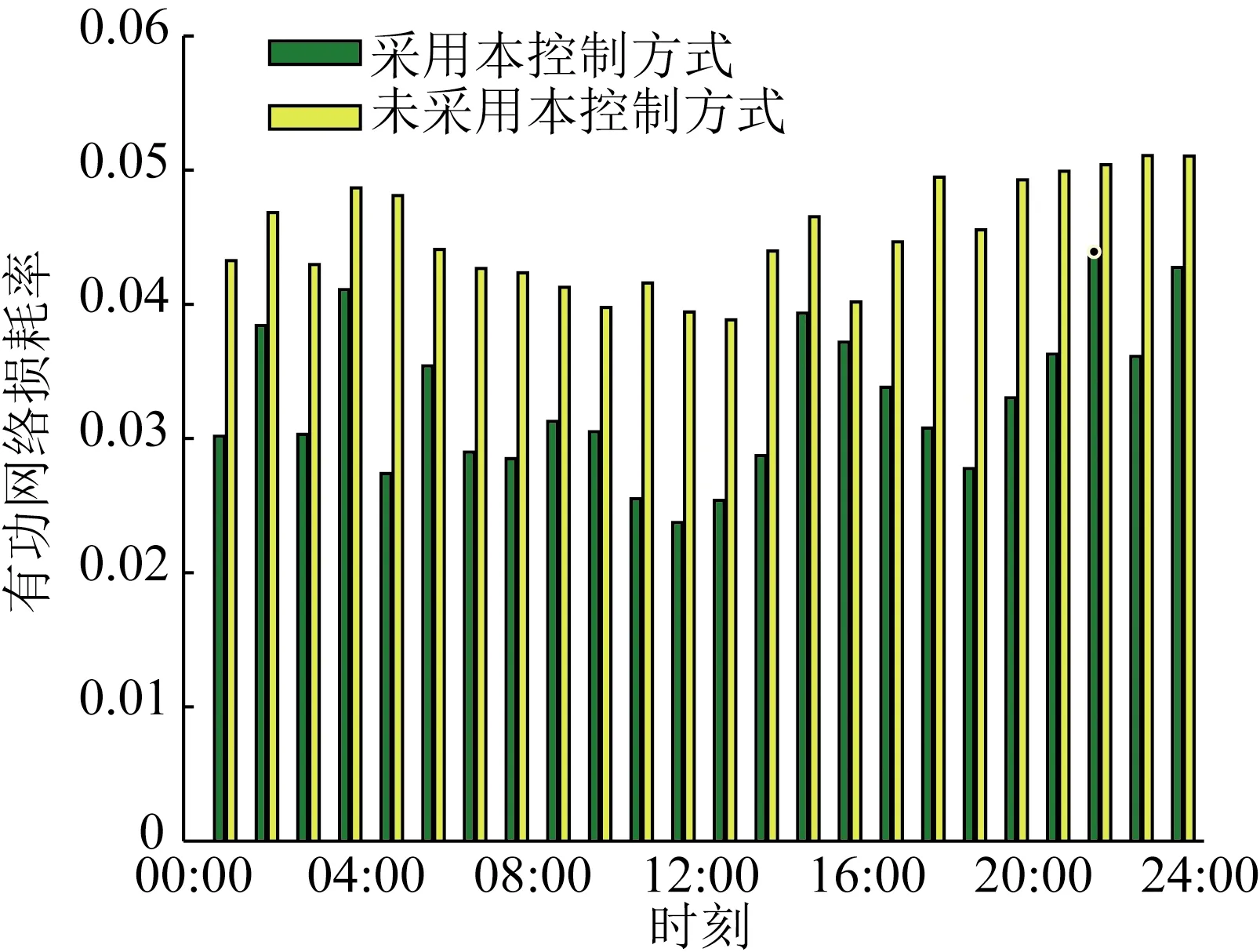
图11 有功网络损耗率对比

新能源损耗率如图13所示，由图13可以看出，在采用文本提出的控制方式后，新能源损耗率wm_new最高为20.7%，其他时刻除17:00出现过15.5%外，其余都在5%以下，而未采用本文此控制方式时wm_new在相同时刻下均大于或等于采用本文所提控制方式下的wm_new，且有1/3时刻都在15%以上。图14为储能电站参与前后新能源出力损耗情况，由图14可以看出，与储能电站参与调控前相比，光伏、风电功率出力值与实际并网功率值的差值减小，储能电站有效提高新能源的消纳，减少了风电、光伏的能源浪费。

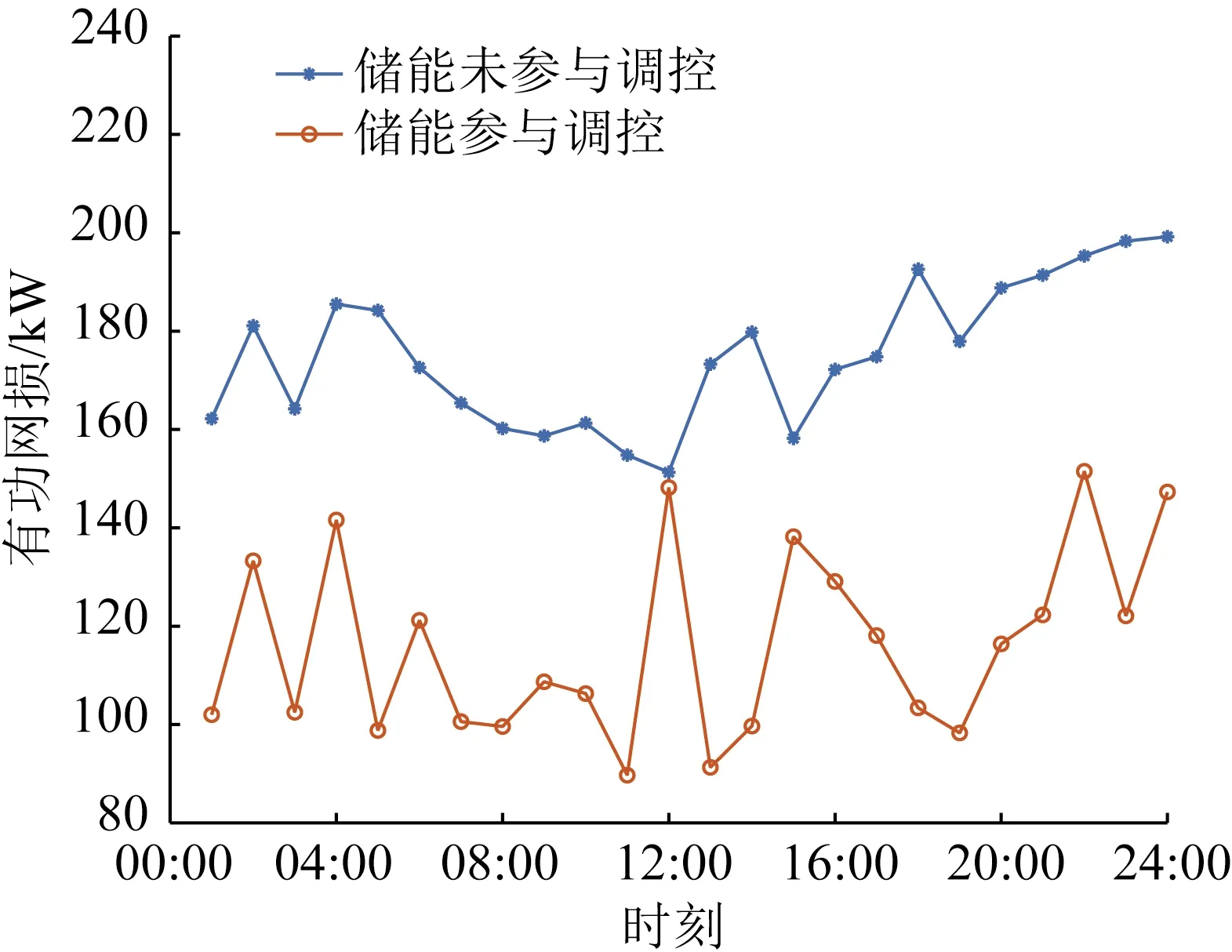
图12 储能参与前后有功网损对比

图13 新能源损耗率对比

图14 储能参与前后新能源出力损耗对比

5 结 论

本文针对含新能源并网的配电网提出了一种分时间尺度执行的DESS双层控制策略，使系统更加安全经济地运行。通过算例分析可知，相较于以往储能系统仅用来进行削峰填谷来说，采用此控制策略后可有效提高储能电站利用率。并且可以看到，在相同运行情况下，未采用本文控制策略时任一储能电站每隔15 min都会进行一次充放电，而采用本文控制策略后节点7、12、26处储能电站充放电次数均为3次，储能电站的充放电频率得到了有效降低。

当间歇性新能源出力或负荷突变造成电压失稳，储能电站的参与不仅能够实现快速响应，还可增加新能源消纳率，减少有功损耗。储能电站采用本文控制方式前后的新能源损耗率均值分别为8.10%、2.54%，下降了5.56%，有功网络损耗率均值分别为4.5%、3.3%，下降了1.2%。此控制策略中短时间尺度控制先进行电压稳定判断再决定是否执行双层控制的方式，可减少系统计算复杂度，节省数据占用空间。