改进地标点采样的加速谱聚类算法
2021-05-12徐航帆唐坚刚彭敦陆
徐航帆,刘 丛,唐坚刚,彭敦陆
(上海理工大学 光电信息与计算机工程学院,上海 200082)
现今世界数据量爆炸增长,对大数据进行高效地分析将在各行各业起到关键性作用。聚类分析[1]是一种无监督学习方法,也是数据挖掘和机器学习中一个重要的研究方向。聚类是指将数据在不需要先验知识的情况下根据某种相似度划分为多个簇的过程。传统的聚类算法,例如K-means算法[2]具有简单高效的特点,在球形结构的数据上有着较高的聚类精确度。但是,其缺乏处理复杂结构数据的能力[3]。当样本空间为非凸时,K-means算法往往达不到理想的效果[4]。
为了能在任意形状的样本空间上聚类,且收敛于全局最优解,研究人员开始研究新型的聚类算法,也被称为谱聚类[5]算法(Spectral Clustering Algorithm,SC)。谱图理论[6]是该算法的理论基础,其本质是将聚类问题转化为图的最优划分问题。近几十年来,研究人员提出了多种谱聚类算法,例如Ratio Cut算法[7]和Normalized Cut算法[8]。这两种算法将数据转换为基于相似性的加权无向图, 然后通过图优化算法进行求解。文献[9]提出了NJW算法,该算法是一种应用比较广泛的谱聚类算法。然而谱聚类算法在面对大规模数据集时,其构建相似度矩阵所需的空间复杂度(O(n2))和拉普拉斯矩阵特征分解所需的时间复杂度(O(n3))十分庞大,产生的计算成本将难以承受。
为了克服谱聚类的在大数据集上的可扩展性问题,一些加速谱聚类的算法被提出来,其中最自然的想法就是降低拉普拉斯矩阵的特征分解时间。2004年,文献[10]采用经典的Nyström[11]方法有效地计算了特征分解的近似解,从原始数据集中随机选取p个样本,然后计算相似度矩阵W∈p×p,根据这个矩阵计算特征分解来近似表示原始相似度矩阵的特征分解。文献[12]提出了可扩展的Nyström方法,通过随机低秩矩阵近似算法大大减少了算法的运行时间。文献[13]提出了一种自适应采样的方法,改进了Nyström谱聚类算法的聚类效果。
后来,文献[14]提出了一种通过地标点表示的加速谱聚类算法(Landmark-based Spectral Clustering,LSC),其效果优于前述算法聚类。该算法中,需首先对原始数据进行采样,选取p个地标点,通过p个点与原始n个数据点成对相似度来构建相似度矩阵Z∈n×p。然后,利用稀疏编码技术[15]调整矩阵Z,使其成为稀疏相似度矩阵[16],从而将计算特征分解的时间复杂度降低为O(p3+p2n)。文献[14]提出了两种采样算法:(1)随机采样选取地标点;(2)K-means算法采样选取聚类中心作为地标点。经实验证明,K-means采样在大部分数据集上的最终聚类精确度比随机采样要高,但K-means采样选取的地标点需重复读取数据,时间复杂度大。随机采样选取地标点随机性较大,地标点有时往往选取的不够均匀,效果较差,文献[17]提出了一种基于Pagerank算法选取地标点的方法,通过构建数据点之间成对相似度矩阵W∈p×p选取地标点,并将该方法通过并行计算框架实现,有效减少了运行时间,获得了更好的聚类精度。但是该算法的空间复杂度(O(n2))较大,面对大型数据集时需要更多的计算节点,成本较大。文献[18]提出了一种快速地标点选取算法,有效保留了数据的原始信息,在聚类精度和时间复杂度之间取得较好的平衡,但该方法仍会受到离群地标点的影响。
综上所述,基于地标点的加速谱聚类算法存在以下两个问题:(1)地标点的选取难以在时间空间成本和最终聚类精度之间保持有效平衡;(2)聚类结果易受分布不均匀地标点和离群地标点的影响。
针对上述问题,本文提出了改进地标点采样(Improved Landmark Selection,ILS)的加速谱聚类算法(LSC-ILS)。该方法通过随机多组待选地标点集,根据地标点之间相似度标准差信息,选择分布最均匀的地标点集,结合地标点周围原始数据点局部密度分布信息,去除周围原始点局部密度分布较小的离群地标点。实验证明此算法能用较少的时间成本获得较高的聚类精确度,在时间空间成本和聚类精度上取得较好的平衡。
1 相关工作
1.1 谱聚类
给定数据集X={x1,x2,…,xn}∈m×n,其中n表示样本个数,m表示数据维度。谱聚类首先根据数据点之间成对相似度矩阵W∈n×n构造无向G=(V,E),其中W中第i行第j个元素wij≥ 0表示点xi和点xj之间的相似度。X中的样本点对应V的顶点,任意两点之间权重由W给出。度矩阵D是由相似度矩阵W的行和组成的对角线矩阵,如式(1)所示。
(1)
L=D-W被称为拉普拉斯矩阵。然后谱聚类对拉普拉斯矩阵进行特征分解,并对前k个最小特征值对应的特征向量组成的点进行聚类(一般利用K-means聚类算法),作为最终聚类结果。基础谱聚类算法流程如下文所示。
输入:n个数据点x1,x2,x3,…,xn∈m;聚类数目k。
输出:聚类结果标签。
步骤1根据数据点之间相似度构造相似度矩阵W∈n×n,根据式(2)计算度矩阵D∈n×n;
步骤2根据拉普拉斯矩阵L=D-1/2(D-W)D-1/2计算前k个最小特征值对应的特征向量,组成点集Q={q1,q2,…,qk};
步骤3Q的每一行视作一个点,通过K-means算法得到最终聚类结果。
由于传统谱聚类算法空间复杂度(O(n2))和时间复杂度(O(n3)),很难将其扩展到大规模数据集的应用。因此本文提出了扩展到大规模数据集上的加速谱聚类的算法。
1.2 基于地标点的加速谱聚类算法
基于地标点的加速谱聚类算法是一种在大规模数据集上加速谱聚类的方法。该算法通过矩阵分解技术找到一组点,通过这组点与原始点之间的关系来近似表示原始数据。X={x1,x2,…,xn}∈m×n是原始数据矩阵,矩阵分解技术就是找到p个m维的数据点集U∈m×p和与原始点的关系矩阵Z∈p×n,通过式(2)近似表示原始数据矩阵X。
X≈UZ
(2)
式中,矩阵U为地标点集,每一列为每一个地标点,这些地标点为原始数据点的代表点。对于任意一个数据点xi∈X,它的近似点φi可以通过式(3)表示。
(3)
式中,uj是U中第j列向量,表示第j个地标点;zji是矩阵Z中第j行第i列的元素。如果uj不在点xi最近的r(≤p)个邻域中,则zji置为0,因此Z就变成了稀疏表示矩阵。通过U(i)∈m×r表示U的子矩阵,由xi的r个最近的地标点组成。zji可由式(4)计算。
(4)
K(·)是和函数,通常使用高斯核函数
(5)
根据矩阵Z计算相似度矩阵W,如式(6)
W=(D-1/2Z)T(D-1/2Z)
(6)
其中,D是一个p×p对角矩阵,由Z的行和构成。D-1/2Z的奇异值分解(Singular Value Decomposition,SVD)如下
D-1/2Z=AΣBT
(7)
其中,Σ=diag(ß1,ß2,…,ßp),ß1≥ß2≥…≥ßp≥0是D-1/2Z的奇异值;A={a1,a2,…,ap}∈p×p是左奇异向量矩阵;B={b1,b2,…,bp}∈n×p是右奇异向量矩阵;ßi2为特征值。很明显,B的列向量为W的特征向量,A的列向量为(D-1/2Z)(D-1/2Z)T的特征向量。
由于矩阵(D-1/2Z)(D-1/2Z)T的维度是p×p,可以先计算A,只需要O(p3),B因此可以由下式(8)计算。
BT=∑-1AT(D-1/2Z)
(8)
由于p≪n,所以拉普拉斯矩阵的分解时间就从O(n3)减少到O(p3+p2n),存储空间由O(n2)减少到O(np),大幅减少了谱聚类所需的时间和空间。
2 改进地标点采样的加速谱聚类算法
地标点的选取作为基于地标点的加速谱聚类算法的最关键部分,在很大程度上决定了最后聚类结果。随机采样的方法在大规模数据上选取的地标点易集中于某一局部区域,分布不均匀。K-means采样算法存在着反复读取数据,时间消耗较大的问题;Pagerank采样算法需先构造数据点之间成对相似度矩阵,空间复杂度较大。此外,聚类结果也易受离群地标点的影响。针对以上问题,本文提出了改进地标点采样的加速谱聚类算法。该算法首先多次随机采样选取多组地标点集,计算各组地标点之间相似度的标准差(Standard Deviation,SD),通过标准差来衡量地标点的均匀程度;然后计算地标点周围原始数据点密度分布来衡量地标点的代表性,去除代表性较差的离群地标点,进一步在不影响聚类精度的情况下减少时间复杂度。
2.1 改进的地标点采样算法
给定数据集X={x1,x2,…,xn}∈m×n,其中n表示样本个数,m表示数据维度。首先通过均匀随机采样,从原始数据集中进行c次地标点采样,每次采样p个地标点,形成c个地标点集,其中第i个地标点集表示为Ui={u1,u2,…,up}∈m×p。为了选择最佳的地标点集,通过地标点集Ui中点之间成对相似度矩阵Si∈p×p的行标准差之和来衡量地标点的分布均匀程度。其中,点uj与点ul之间相似度计算如式(9)所示。
(9)
其中,K(·)是核函数,通常由式(5)计算。
第j行的行标准差计算如下
(10)
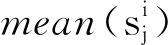
(11)
各个地标点集的行标准差之和即为SD={SD1,SD2,…,SDc},其中max(SD)对应的地标点集Ui={u1,u2,…,up}为最佳地标点集。
接下来,计算各个地标点的局部密度权重,通过局部密度权重反映地标点周围原始数据点的分布情况。局部密度权重越大表示地标点周围数据点分布越密集,地标点就越重要,局部密度权重越小表示地标点周围数据点分布越稀疏,地标点就越不重要;然后去除密度权重小于阈值γ的地标点(Landmarks Reduction,LR)。具体步骤为:首先构造地标点与原始数据点之间的相似度矩阵Z′∈p×n,z′ji表示第j个地标点与原始数据点xi之间的相似度,计算式为
(12)
其中,K(·)是核函数,通常由式(5)计算;然后计算每个地标点的密度权重。地标点uj权重dj计算如下
(13)
其中,count(z′ji>s,z′ji∈z′j)表示原始样本中与地标点uj相似度大于s(0~1)的数量;最后根据阈值γ(0~1),选出权重dj>γ的p′个地标点。
2.2 改进地标点采样的加速谱聚类算法流程
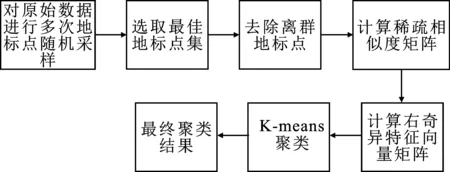
图1 LSC-ILS流程图
图1为改进地标点采样的加速谱聚类算法流程,其具体流程如下文所示。
输入:原始数据集X={x1,x2,…,xn}∈m×n,地标点数量p;系数相似度矩阵近邻个数r;地标点集个数c;阈值s和γ;聚类数目k。
输出:聚类结果标签。
步骤1对原始数据集进行c次随机采样选取c个地标点集U={U1,U2,U3,…,Ui,…,Uc};
步骤2根据式(9)计算每个地标点集的相似度矩阵Si;
步骤3根据式(10)和式(11)计算出每个地标点集相似度矩阵的标准差SDi;
步骤4计算max(SD),输出其对应的地标点集;
步骤5根据式(12)计算地标点密度权重dj;
步骤6选出阈值dj>γ的p′个地标点;
步骤7根据式(5)计算地标点与原始数据点之间的稀疏相似度矩阵Z;
步骤8计算(D-1/2Z)(D-1/2Z)T的前k个最小特征值对应的特征向量A={a1,a2,…,ap′};
步骤9根据式(7)计算B={b1,b2,…,bp′};
步骤10B的每一行视作一个点,通过K-means算法得到最终聚类结果标签ri∈R。
2.3 时间复杂度和空间复杂度分析
本节是对本文算法的时间复杂度和空间复杂度分析。数据样本数量为n,采样次数为c次,每次采样地标点数量为p,最后输出地标点数量为d,其余算法采样地标点数量为p。
采用随机采样选取c组待选地标点的时间复杂度可以忽略不记,构建地标点相似度矩阵需要O(cp2)的时间复杂度,需要O(cp2)空间复杂度。根据地标点与原始点之间的相似度矩阵计算地标点密度权重以及构建稀疏相似度矩阵需要O(pn)时间复杂度。计算稀疏相似度矩阵需要O(pn2),根据稀疏相似度矩阵计算左奇异向量需要O(d3)的时间复杂度,计算右奇异向量需要O(d2n)的时间复杂度。

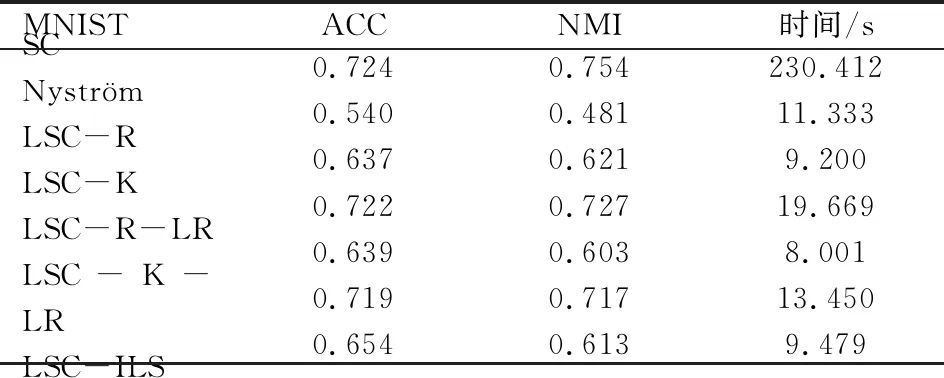
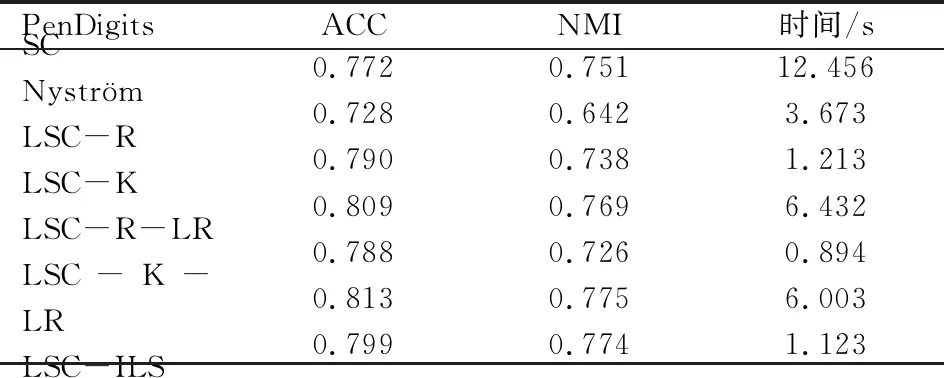
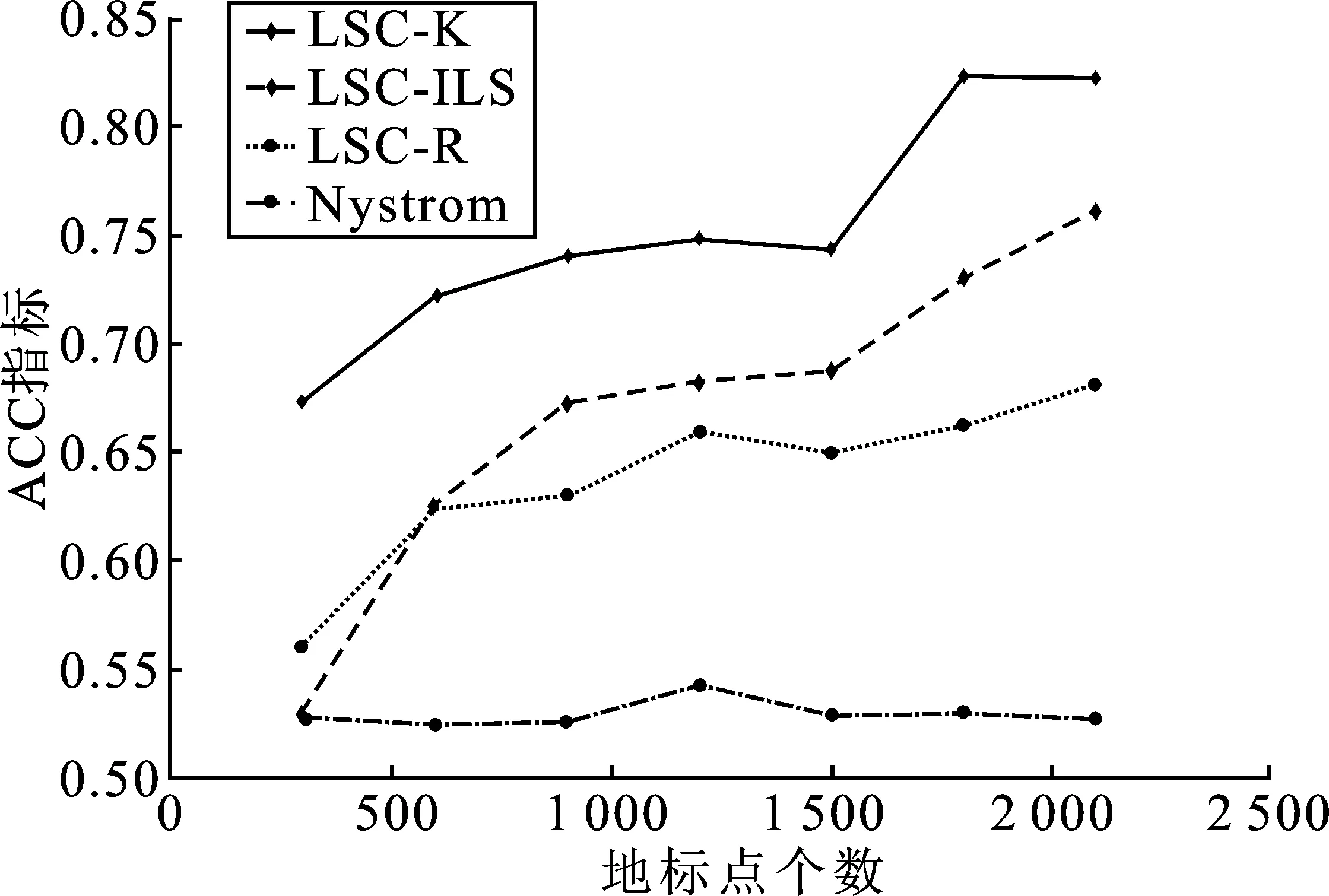
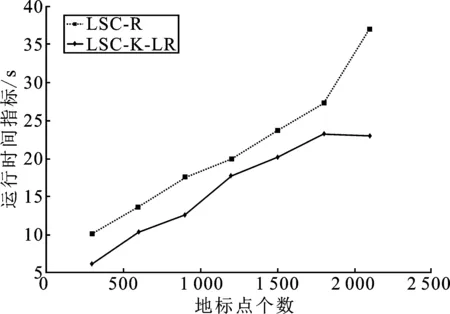
表1 时间复杂度分析 (p≪n,d 表1是4种算法的时间复杂度分析,由表1可以看出本文算法的时间复杂度总和最小。 为了验证本文算法的有效性,进行实验分析,从算法的聚类精确度和运行时间两指标进行评估。本文选取原始谱聚类[5](记为SC)、Nyström 近似谱聚类[11](记为Nyström)、基于随机采样的地标点谱聚类[13](记为LSC-R)和基于K均值中心的地标点谱聚类[13](记为 LSC-K)与本文算法(记为LSC-ILS)进行对比。为了证明本文提出的去除地标点算法(LR)有效性,本文将LSC-R和LSC-K分别结合LR算法(记为LSC-R-LR和LSC-K-LR)与原始LSC-R和LSC-K算法进行实验比较。 为了验证本文算法面对大规模数据集的性能,选择两个大规模UCI数据集进行实验。第一个为MINIST,该数据集是一个手写数字的数据集,共有70 000个样本,共10类,每个样本被视为784维数据。第二个为Pendigits,该数据集也是一个手写数字的数据集,包含了44个作者写的250个手写样例,经过处理得到10 992个样本,每个对象有16个属性,共被分成10类。 为了评价聚类有效性(聚类算法对数据进行划分的正确程度),本节采取了两个指标,即聚类精确性(Accuracy,ACC)[19]和标准化互信息(Normalized Mutual Information,NMI)[20]进行数值分析。实验在英特尔Core i3-8100@3.6 GHz,8 GB内存的计算机上运行,代码在MATLAB环境下编写。 给定数据点xi,令ri∈R和fi∈F分别为聚类结果标签和预定义标签,ACC定义如下 (14) 式中,n是样本数量;δ(x,y)表示若x=y,为1,否则为0。map(ri)是聚类结果标签ri映射到数据语料库中的真正标签,采用Kuhn-Munkres算法[21]可以找到最佳映射。 MI(R,F)互信息表示为 (15) 式中,p(ri)和p(fj)是从数据集中任意选择的样本属于标签ri和标签fj的概率;p(ri,fj)是从数据集中任意选择的样本属于簇ri和fj的联合概率。NMI标准化互信息计算如下 (16) H(R)=-∑ri∈Rp(ri)logp(ri) (17) 式中,H(R)是聚类结果R的熵,表示R中变量的混乱程度,R中变量越混乱,H(R)的值越接近1;反之H(R)的值越接近0。很明显ACC指标和NMI指标取值范围都是[0,1],越接近1表示聚类结果越精确。 7种聚类算法在MINIST和Pendigits上的聚类结果如表2和表3所示,聚类指标分别为聚类精确度(ACC)和标准化互信息(NMI)。为了比较的公平性,6种加速谱聚类算法的抽样数均为1 000,基于地标点的加速谱聚类算法稀疏相似度矩阵的最近邻个数r为5。其中,本文算法中s参数,γ参数和c参数均为人工设定,选取较优的值。 表2和表3分别表示MINIST数据集和Pendigits数据集熵算法的各项指标对比。 表2 MINIST数据集上算法性能对比 表3 Pendigits数据集上算法性能对比 由表2和表3中可以看出,本文算法LSC-ILS聚类精度比Nyström和LSC-R算法高,比LSC-K算法低,运行时间短于LSC-K算法和Nyström算法,与LSC-R算法运行时间几乎持平。LSC-R-LR算法和LSC-K-LR算法的聚类精度分别与LSC-R算法和LSC-K算法几乎持平,但运行时间有所减少。因此,综合聚类精确度与运行时间本文算法做到了更好的平衡,并且本文中LR算法可扩展到其它算法中,在保持聚类精确度的情况下减少运行时间。 为了验证地标点个数对加速聚类算法的影响,将本文算法与其余3种加速谱算法在数据集MINIST上针对不同地标点数量在3个指标上进行对比。地标点数量从300开始,增量为300,到2 100结束,结果如图2~图4所示。 图2 MINIST数据集上ACC指标随地标点增长变化 由图2~图4可以看出,除了Nyström算法,其余算法的聚类精确性均随着地标点个数增加而增加。本文算法聚类精确度始终保持在LSC-K与LSC-R之间,但运行时间几乎与LSC-R算法持平,远小于LSC-K算法,运行时间增长慢于LSC-K算法,并且随着地标点个数的增加,本文算法精确度增长加快。 图3 MINIST数据集上NMI指标随地标点数量增长变化 图4 MINIST数据集上时间指标随地标点数量增长变化 为了进一步验证本文中LR算法对LSC-R和LSC-K算法随地标点数量增长的变化的影响,将LSC-R和LSC-K分别与LSC-R-LR和LSC-K-LR在数据集MINIST上针对不同地标点数量在3个指标上进行对比。地标点数量同样从300开始,增量为300,到2 100结束。结果如图5~图10所示。 由图5~图10可以看出,LSC-R-LR算法和LSC-K-LR算法在不同的地标点数量情况下的聚类精度几乎与LSC-R算法和LSC-K算法持平,运行时间有所减少,进一步证明了本文LR算法的稳定性和有效性。 图5 ACC指标随地标点数量变化 图6 NMI指标随地标点数量变化 图7 Time指标随地标点数量变化 图8 ACC指标随地标点数量变化 图9 NMI指标随地标点数量变化 图10 Time指标随地标点数量变化 本文针对传统加速谱聚类算法存在的一些问题提出了改进地标采样的加速谱聚类算法。通过多次随机采样选取多组地标点集,利用各个地标点集内地标点之间相似度矩阵的行标准差和衡量地标点的分布情况,选取最佳地标点集,并根据地标点的密度权重去除一些离群地标点。本文从理论和实验分析证明了该算法的有效性。下一步计划将本文算法扩展到分布式计算框架上,进一步提高算法效率。3 实验验证
3.1 数据集
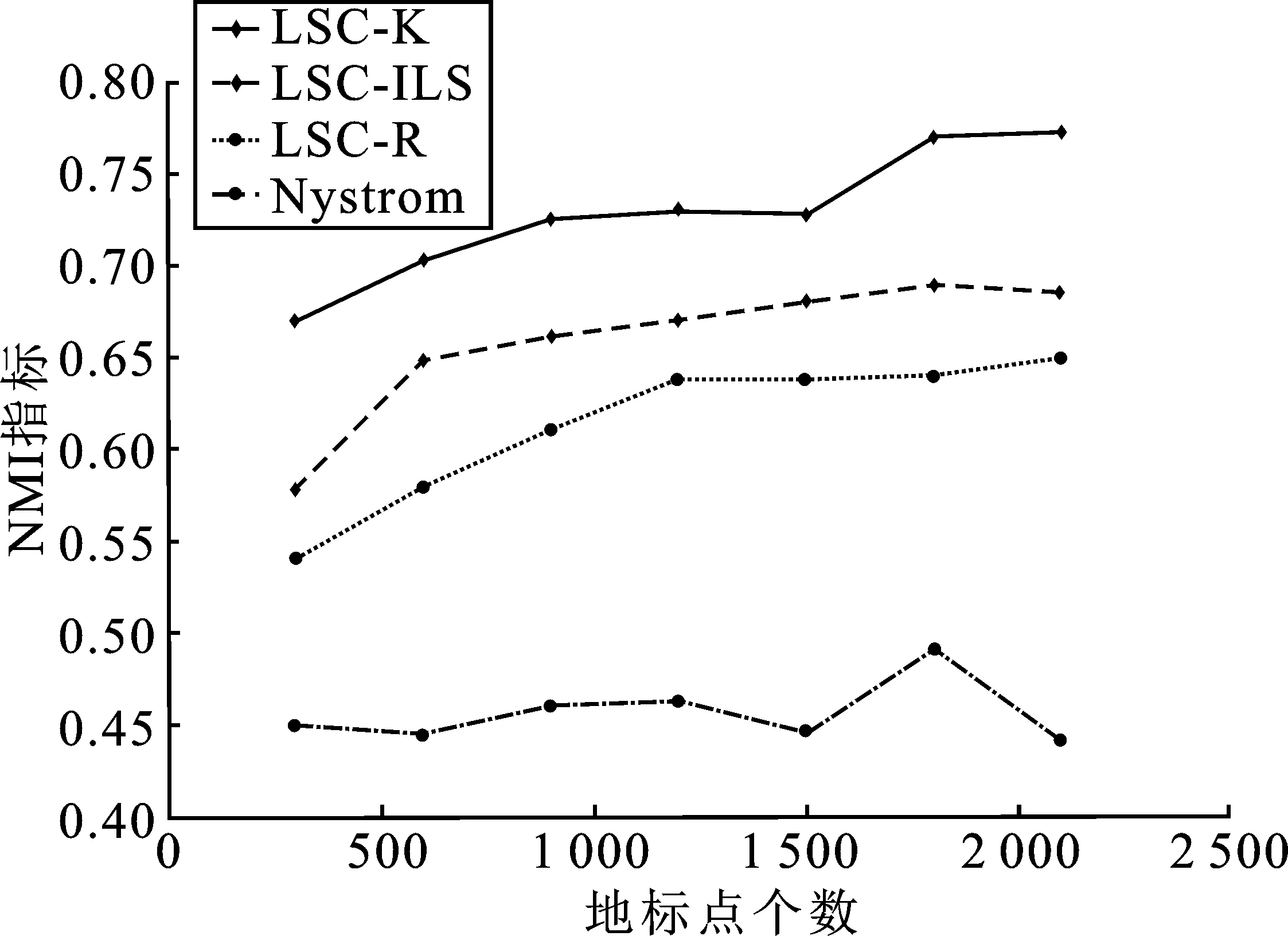
3.2 评价指标
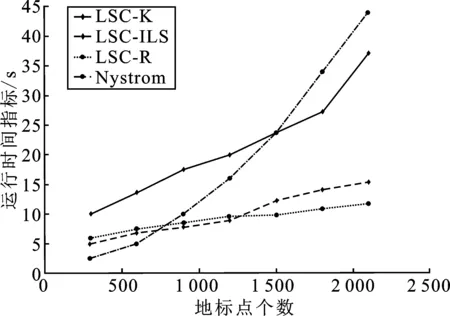
3.3 实验结果
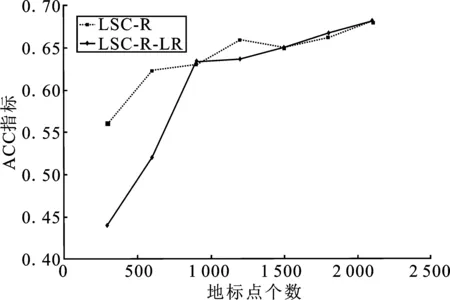
4 结束语
