流场压缩感知渗透率计算

郭 龙，姚树新，郑法威

(1.中海油信息科技有限公司，广东 深圳 518000；2.中国科学院 深圳先进技术研究院，广东 深圳 518000)

多孔材料(例如吸附剂、锂电池、岩石、建筑材料等)的评价检测过程中均需要对其进行计算机断层扫描(Computed Tomography，CT)，从而得到三维多孔介质模型，然后对模型进行渗透率分析。这种模型渗透率分析需要计算流体动力学(Computational Fluid Dynamics，CFD)技术。流体模拟目前是计算机算法的一个重要研究分支[1]。基于工程物理中的流体力学模型，已有众多计算研究对CFD算法进行了优化。渗透率计算的准确程度通常与流体的细节相关，例如在地质学上要计算出更精确的数字岩心渗透率，即需要更多的网格采样点。网格点的增多使计算开销增大，导致模拟速度变慢，同时也引起了内存需求增加。

钻井时，通过岩屑迅速CT扫描工具，可获得数字岩心并求取在钻地层的渗透率。但钻井速度较快，要得到实时的渗透率信息，仍需要长时间的流体模拟与三维渲染，这使得数字岩心扫描方法的速度优势已不存在。因此众多研究者们致力于探寻各种方法，在加快流体模拟速度的同时保证模拟的细节。通过细节质量确保最终计算结果准确与实时的计算要求。

流体模拟的两大类基本方法为：欧拉网格法与拉格朗日粒子法。其中，欧拉网格法在空间中设置固定的网格采样点，通过求解流体方程得到短时间内网格上速度、压强、密度[2]。文献[3]用格子玻尔兹曼方法(Lattice Boltzmann Method，LBM)得到了Nnvier-Stokes(NS)方程的数值解，并用该方法进行三维多孔介质内渗透率的计算。拉格朗日粒子法处理流体为小颗粒组成的粒子系统，使每个颗粒与周围颗粒互相作用，以求解短时间内粒子的速度、加速度、位置等变化[4]。光滑粒子动力学(Smoothed Particle Hydrodynamics，SPH)[5-6]是一种经典的粒子法。在渗透率计算中，粒子法的时间复杂度随粒子数以几何倍数增加，且精度较低；而欧拉网格法的数值精度高且便于实现，是较为常用的方法。

欧拉网格的LBM求解器可分为：碰撞、迁移、计算宏观量、边界处理共4个步骤。网格等同于流场的采样点，也将压缩感知中的采样点与流场格子相对应。渗透率计算需要统计每个格点的瞬时流量，为减小误差，通常采用如下3种方法在计算量与精度之间平衡：(1)自适应网格；(2)额外细节；(3)模型缩减。

欧拉方法通常使用自适应网格节省计算资源。文献[7]使用了八叉树网格优化采样格点。文献[8]用粗网格投影，先计算粗网格，再使内部细网格满足无散条件。欧拉网格也可以在粗网格模拟的基础上，添加湍流细节，例如文献[9]在粗网格上的工作。欧拉网格的模型缩减法通过数据降维，降低计算的复杂度。文献[10]在2006年首次使用主成分分析了将满足不可压缩条件的高精度速度场进行降维，获得代表流场特征的正交基，然后在低维模型中求解方程。结果表明，其模拟效率大幅提高，但精度也相应地显著降低。文献[11]在其基础上将模拟场景进行分块降维再重新拼接，获得了在超大尺度空间实时模拟的效率。以上优化方法均可减少欧拉方法的计算量，但基本都是以精度大幅下降为代价。传统网格取样受限于经典的Nyquist采样理论，在计算时无法将采样数量降至定理指出的最小采样数。因此，需要借助压缩感知(Compressive Sensing，CS)突破Nyquist采样理论的限制，从而降低粗网格计算量，然后再恢复到高精度计算结果。由文献[12～14]建立起的压缩感知理论，颠覆了Nyquist经典采样定理。其建立了数学理论框架，在满足一定的限制条件下，可以通过一些重构优化算法从少量的采样数据中较好地还原出原始数据。

1 渗透率计算步骤

1.1 使用LBM求解NS方程组

Navier-Stokes方程组是一组描述粘性不可压缩流体运动的方程。用于生成速度场的NS方程组为

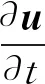
(1)

式中，ρ是流体的密度；u是流体的速度；t是时间。网格中每一个采样点上均有一个带方向的速度矢量，组成了一个速度场。三维空间的每个速度矢量有3个分量，分别展开成ux、uy、uz标量场，后续压缩感知可处理的数据即是这种标量场切片。g是外力对格点内密度造成的加速度，v是流体的粘滞系数。在统计物理学中，式(1)等价于Boltzmann方程的粒子速度分布描述函数。文献[15]指出了格子玻尔兹曼方程是玻尔兹曼方程的有限差分求解形式，即LBM可以通过差分格式求解NS方程。Boltzmann-BGK方程对粒子速度分布函数f时空变化进行了描述[16]

(2)

式中，f=f(x，c，t)是粒子速度分布函数；c为格子上的离散速度；g为外力及表面力产生的加速度；f对c的偏导数是速度空间中的单方向导数；τ为上述单一松弛时间模型中的特性松弛时间。在方程右侧是BGK碰撞模型，其中feq是无量纲的离散速度空间的局部平衡态分布函数。选择合适的f是构造格子Boltzmann模型的关键，而f的形式与构造离散速度模型相关。文献[15]提出的DnQm系列模型是目前被广泛应用的模型，其中n表示维数，m是离散速度c的方向个数。D2Q7、D2Q9、D3Q15模型，如图1所示。

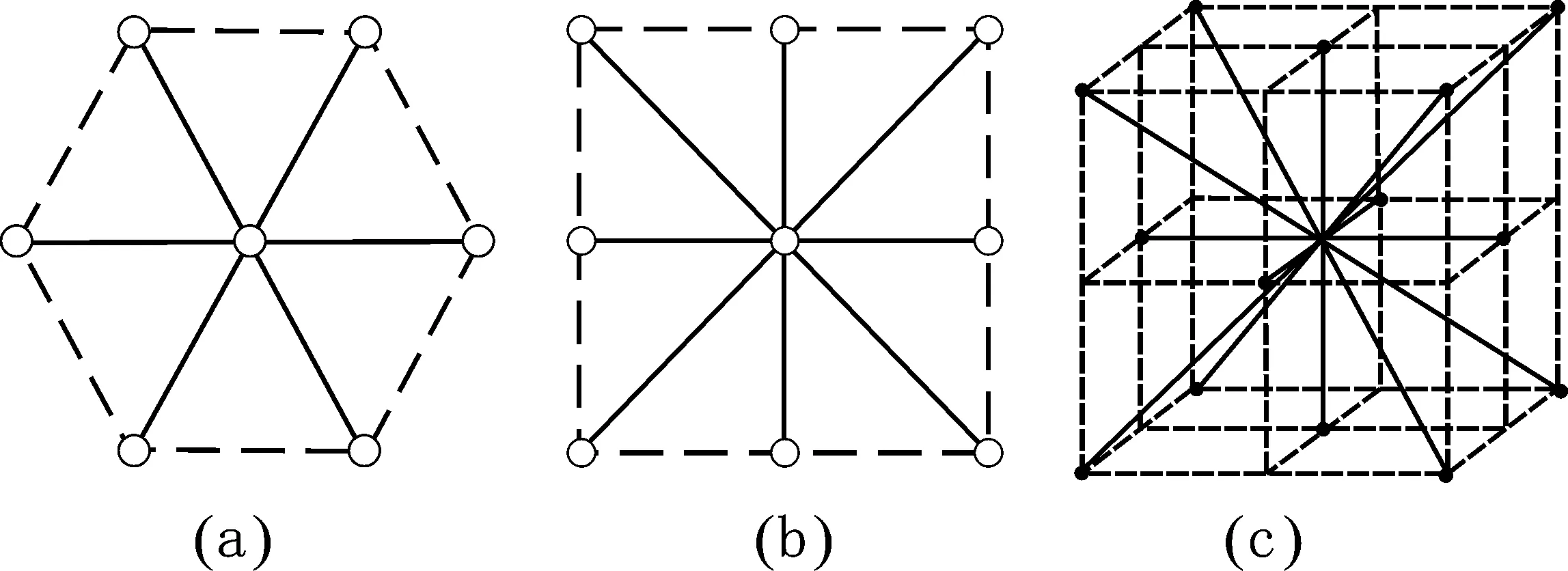
图1 DnQm系列模型的离散速度方向

这类模型的f可以写成以下形式

(3)

式中，cs是格子的声速，也是一个常数；ρ是当前格子的流体密度；u是瞬时的流体速度；ci是本格子第i个方向的离散速度；wa是权系数。通过替换等式中的平衡速度ueq来实现外力(或压力梯度)作用。

(4)

其中，F为外力项，其在速度u的坐标轴x、y、z方向上分解后，可以以加速度g=τF/ρ的形式与速度分量相加得到平衡速度。由外力作用后的f(t+Δt)，以式(5)的形式传播迭代。从而完成一次“碰撞、迁移、计算宏观量、边界处理”计算循环。

(5)

式中，Δt为一次迭代所消耗的格子时间，其需要经过格子尺度转化为真实世界时间，具体模拟方法已较为成熟，本文不再赘述。在同样的真实世界尺度下，不同精度的网格计算渗透率具有差异。如图2所示，在100×41×41的管道模型中，格子数量降低至10×5×5。则本该是近似抛物面包围面积的区域被线性插值包围面积所替代，从而造成流场计算误差，影响渗透率的计算。

根据渗透率的定义，速度场在某个方向上的投影切片均为该切片上的渗透率。本文中的流场是指流体速度场。如何在较小网格精度下得到高精度的速度场，从而得到高精度的渗透率计算结果，成为了流场压缩感知的重要问题。

1.2 压缩感知

压缩感知理论[14]可推导出：只要流场截面中包含众多零或通过变换得到一个稀疏域，即可将采样频率降至低于Nyquist采样定理要求的频率，然后通过重构从稀疏流场中恢复高精度流场。压缩感在大量减少流场采样的同时，保证将渗透率较好地计算还原出来。

定义一个n维信号向量r∈Rn，当r中只有k个非零采样点而其余均为0时，若k≪n，则称r是稀疏的。向量r的稀疏度为k/n，而r的l0范数含义是其中非零元素的个数。

‖r‖0=k

(6)

通常流场在x、y、z方向上的分量均不是稀疏的，则需要寻找一种正交稀疏变换方法Ψ将r转换为变换域下的向量s，使得s是稀疏的。常用的稀疏变换方法为离散余弦、小波变换等。变换如式(7)所示。

r=ψs

(7)

式中，Ψ为压缩基，是一个n×n的正交矩阵。再定义一个m维向量b∈Rm，其中m≪n。b是由r通过矩阵M下采样得到的，M为采样基。m×n的感知矩阵A是采样基与压缩基的乘积，即整个压缩感知可用下式表达

b=Mr=Mψs=As

(8)

其目的是从流场截面b中恢复出r。需要求解的精确流场切片即为式(8)解集中最稀疏的解。于是问题转换为求解一个l0范数最小的优化问题

min(‖s‖0) s.t.b=As

(9)

但求解l0范数最小问题是NP难问题。因此，需要放宽优化条件为求l1范数，其含义是向量中各元素的绝对值之和，表达式为

min(‖s‖1) s.t.b=As

(10)

式(10)是压缩感知的基追踪形式。根据式(7)，若希望恢复的是一个N×N的二维高精度流场，则转换成向量r后是一个N2×1的向量，稀疏向量也是一个N2×1的向量s。此时，压缩基Ψ的大小为N2×N2。该矩阵相对较大，计算矩阵乘法时的速度也较慢。因此使用的压缩矩阵是直接与N×N的流场矩阵相乘，对其进行直接变换，不需要将流场数据转换为一维向量。

2 速度场稀疏重建

2.1 稀疏变换方法

考虑到流场在某方向上的分量切片与普通灰度图像的相似性，可以用灰度图像的压缩感知理论来处理流场信息。对于较平滑的斑点图像，主要有两种稀疏变换方法：离散小波变换和离散曲波变换。二维离散小波变换每层变换均会分解为4个大小相同的系数矩阵，其长宽均是被分解数据的1/2。若边长出现非2的幂次数值，则在分解前补0。图3是对一个真实岩心图像计算所得流场切片的Haar小波变换示意图。离散小波变换后的系数矩阵数据量大幅减少，只需用大约10 %的数据即可高概率的还原至原速度场切片。

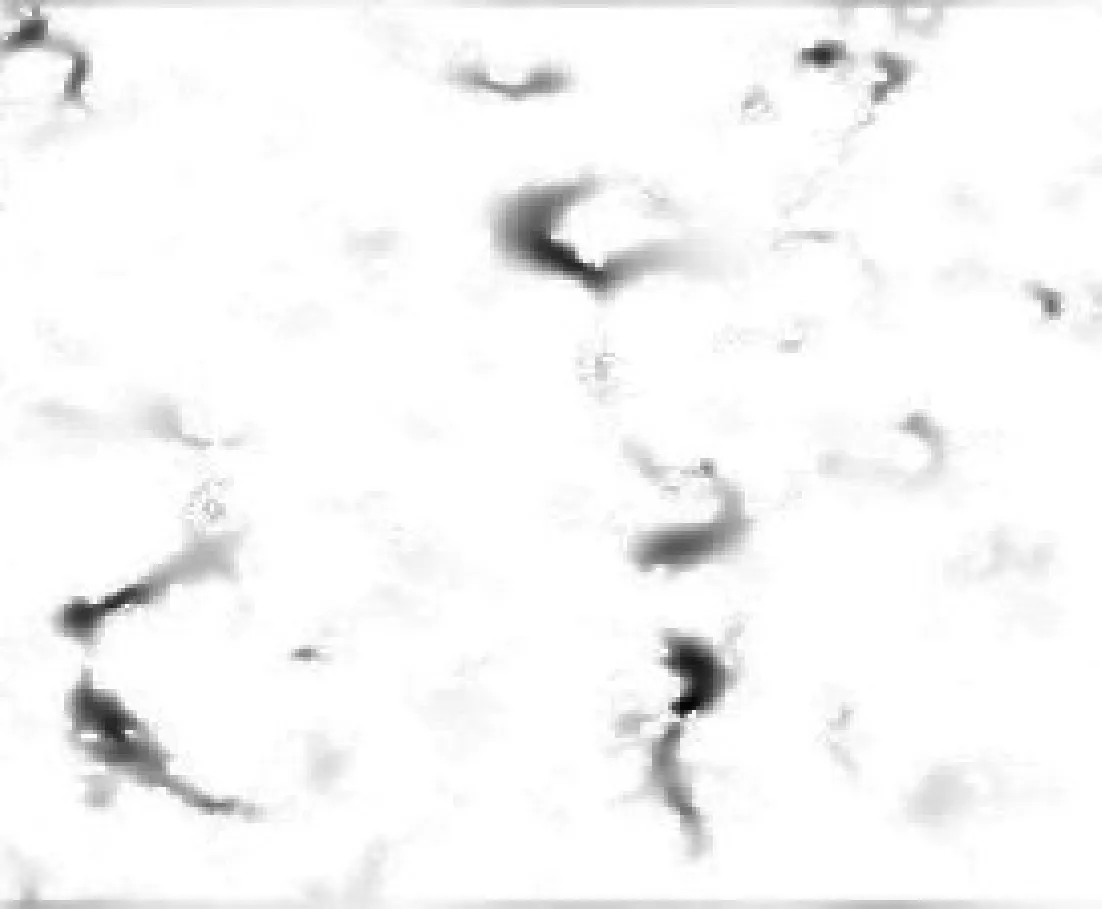
(a)

压缩感知中稀疏度越高，则可在相同数据量下恢复出精度更高的流场信息。本文对比了Haar、Daubechies、Symlets Biorthogonal共3种小波在多层分解条件下的稀疏度，如表1所示。

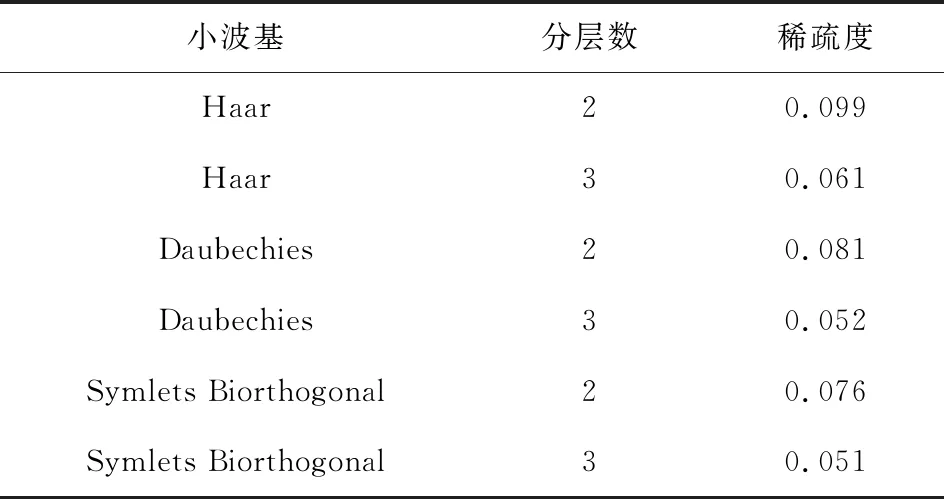
表1 流场切片在多种子波压缩感知中的稀疏度

表1中的数据显示，使用Symlets Biorthogonal小波比Haar与Daubechies变换后的矩阵稀疏度更小。考虑到小波基较多，限于篇幅，本文使仅对比几类常用的小波基。下文中所对比使用的小波变换默认采用Symlets Biorthogonal小波基。

曲波变换(Curvelet)是基于傅里叶变换与小波变换的高度各向异性的一种改进，常用于恢复图形边缘和抑制周边噪声。曲波变换各向异性的优势在于拉伸、平移的基础上同时引入了一个旋转变化。本文用MATLAB软件的CurveLab-2.0程序包实现了Wrapping形式的曲波变换，并将曲波变换后得到的系数矩阵稀疏度与小波变换进行比较，如表2所示。通常其在进行渗透率计算时，总是向特定方向上施加一个压力梯度以驱动流体流动，流场在压力梯度方向的投影绝对值明显大于其他方向，造成了各向异性。而二维曲波变换在各向异性图像中生成的稀疏矩阵系数更少，稀疏程度更高，更适合作为流场切片压缩感知的压缩基。

表2 小波变换和曲波变换稀疏度对比

2.2 采样基

通常LBM模拟框架中，使用的是规则网格。缩减网格相当于将高精度速度场r变成低精度流场b的过程。一般低精度流场也是规则网格，若随机采样，则采样点是不规则网格难以匹配，因此下文使用均匀下采样。由于孔隙分布是随机的，这种采样满足随机采样标准。构造的采样矩阵，将网格精度缩减为原来的0.5倍。对于一个N×N的二维高精度流场，其某一方向上的切片是一个N2×1的向量，得到的低精度流场大小为(N/2)×(N/2)，采样信号b是一个N2/4×1的向量。此时采样矩阵M的大小为N2/4×N2，其为一个较大的矩阵。这里将采样矩阵拆分成两个矩阵，在采样时不需要将速度场切片转换为一维向量，而是与两个N×(N/2)的矩阵相乘。该采样矩阵的构造原理如下：当网格数下降至0.5倍原始网格时，需要将2×2的4个数据合成1个位于中心的数据，每个数据双线性插值的系数均为1/2；采样矩阵先左乘流场矩阵得到(N/2)×N的中间结果，相当于对流场切面矩阵的纵向进行单次线性插值，然后用中间结果右乘采样矩阵的转置，相当于再进行了一次横向的线性插值。

(11)

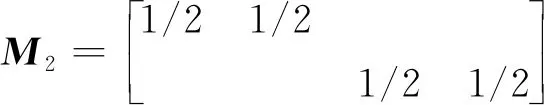
(12)

2.3 流场重构算法

重构算法的主要目的是求解式(10)，即稀疏优化问题。为了解决稀疏优化问题，本文对比了几个高引用率的算法：梯度投影稀疏重建(Gradient Projection for Sparse Reconstruction，GPSR)[17]、谱投影梯度L1最小化(Spectral Projected-Gradient forL1minimization，SPGL1)[18]、快速迭代收缩阈值算法(Fast Iterative Shrinkage Thresholding Algorithm，FISTA)[19]与凸集投影(Projection onto Convex Set，POCS)[20]。在均匀取样的条件下，本文比较了这些取样和稀疏优化的算法。首先进行高精度网格的LBM模拟得到高精度速度场，随机选择其中一个X分量的256×256格子的切片1。然后进行0.5倍精度的网格模拟，得到低精度速度场。如图4所示，在低精度速度场对应切片图4(a)，用压缩感知稀疏重建方法恢复速度场得到切片图4(b)。对比切片1与切片2得到两者的均方误差(Mean-Square Error，MSE)，即可得出不同稀疏恢复方法在流场压缩感知中的适应性，如表3所示。

(a)

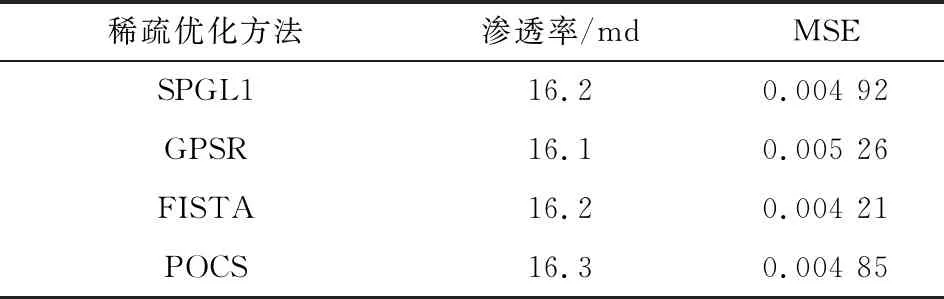
表3 小波变换和曲波变换稀疏度对比

从表3的MSE列可以看出，4种稀疏优化方法求解而恢复出的高精度流场切片与直接用高精度网格计算的结果较相似。原高精度网格计算的渗透率为16.1 md，低精度网格计算的渗透率为15.4 md。4种方法恢复出的切面渗透率与原始高精度流场计算的渗透率最大差0.2 md，从低精度网格恢复的渗透率与高精度网格模拟的结果较为接近。

表4 恢复重构时间对比

作者使用Intel I7-8700K CPU @ 4.7 GHz与双通道16 GB@3.8 GHz内存多线程运行MATLAB，并得到了表4的运行时间数据。切片大小设置为256×256网格，计算流场共进行了2 000次迭代达到平衡态，用时275 ms。若使用1 024×1 024网格计算，则用时2 140 ms。使用高精度的流场计算时间减去低精度计算时间，再减去重建恢复时间即可得到算法节省的计算时间。在4种稀疏优化方法中，GPSR方法和POCS恢复重建速度较快。

3 结束语

本文在多孔介质的渗透率计算LBM模拟中引入了压缩感知，利用切片上1/4的流场采样点，以较低的MSE恢复了高精度的流场信息。基于压缩感知理论，构建了渗透率计算中流体模拟压缩感知采样方法与稀疏恢复方法。

根据计算网格的特性，本文使用均匀采样矩阵作为压缩感知的采样基。对比针对l1范数最小的4种重构算法，且对比了曲波变换、小波变换的多种压缩基的稀疏度。最后，利用实际岩心的256×256切片模拟实际的渗透率计算。从模拟结果中可以看出，压缩感知在渗透率计算中的应用能够将低网格数的速度场切片计算结果恢复到高精度的速度场切片结果，从而提高计算效率。