对一道课本例题的推广

安徽省合肥市第四中学(230000) 周赛龙 储炳南

1 问题的提出

普通高中课程标准实验教科书(人教A 版)数学选修4-4第33 页例3 是这样的:

例题如图1, 已知O是直角坐标原点,A、B是抛物线y2= 2px(p ＞0) 上异于顶点的两动点, 且OA ⊥OB,OM ⊥AB并与AB相交于点M,求点M的轨迹.

下文将具体说明: 在保留题设条件“OA ⊥OB”不变的情况下,该问题有着极其丰富的推广价值.另外,为了使该问题能与函数更好地结合,将题设中的抛物线改为焦点在y轴上的抛物线.

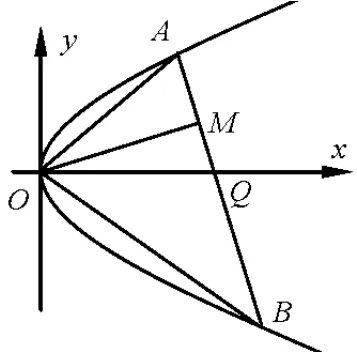
图1

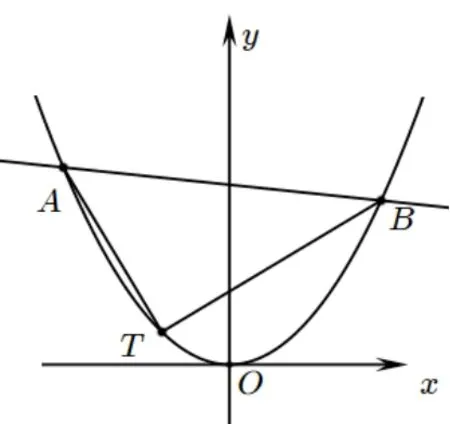
图2

2 问题的推广

结论1(抛物线情形): 如图2, 已知O是直角坐标原点,A、B是抛物线C:x2= 2py(p ＞0) 上异于顶点的两动点,T(2pt,2pt2)是抛物线C上一定点(t ∈R 为常数),且TA ⊥TB,则直线AB过定点Q(-2pt,2p+2pt2).

证明设A(x1,y1),B(x2,y2),Q(x0,y0), 由于直线AB与抛物线必有两个交点, 故可设其方程为:y -y0=k(x - x0), 其中k为直线AB的斜率.联立方程:从而x2-2pkx+ 2pkx0-2py0= 0, 所以x1+x2= 2pk,x1x2= 2pkx0-2py0,由y1- y0=k(x1- x0),y2- y0=k(x2- x0), 得y1+y2= 2pk2-2kx0+ 2y0, 由x21= 2py1,x22= 2py2,得y1y2== (kx0-y0)2, 又因为TA⊥TB, 所以= 0, 因为(x2-2pt,y2-2pt2),所以=x1x2-2pt(x1+x2)+4p2t2+y1y2-2pt2(y1+y2)+4p2t4=0,将

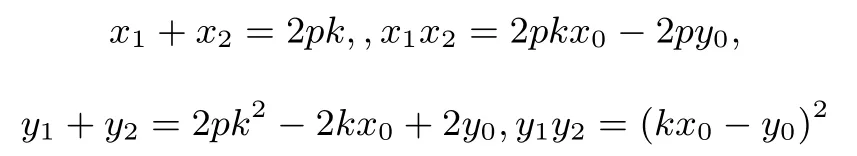
代入上式整理得:

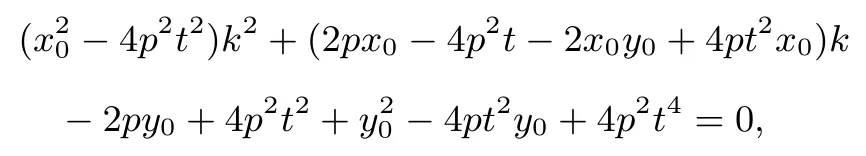
因为当k ∈R 时,上式恒成立,所以

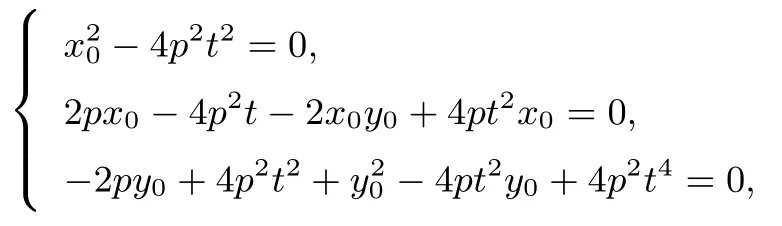
结论2(椭圆情形)如图3, 已知O是直角坐标原点,A、B是椭圆C:1(a ＞b ＞0) 上异于顶点的两动点,T(m,n) 是椭圆C上一定点(m,n为常数), 且TA ⊥TB, 则直线AB过定点

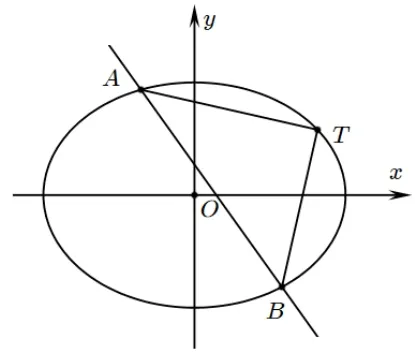
图3

证明设A(x1,y1),B(x2,y2),Q(x0,y0),设直线AB方程为:y-y0=k(x-x0),其中k为直线AB的斜率.联立方程:从而

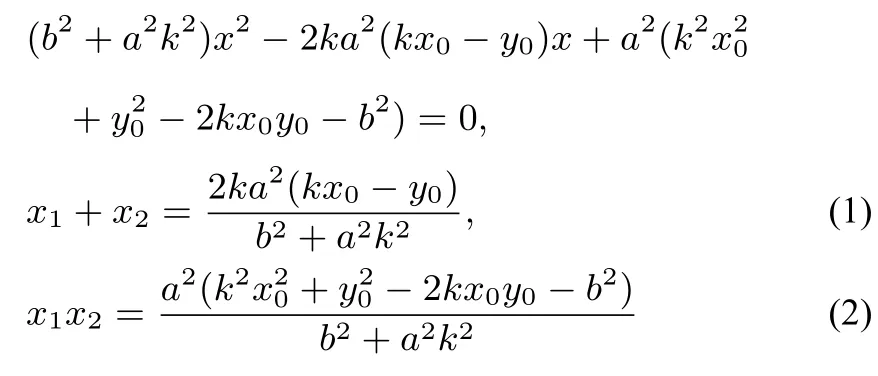
由y1-y0=k(x1-x0),y2-y0=k(x2-x0)得到

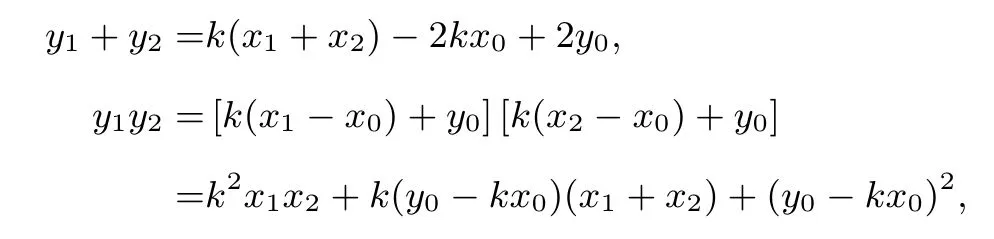
又因为TA⊥TB,所以

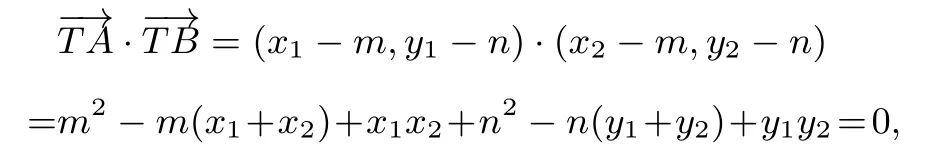
将y1+y2=k(x1+x2)-2kx0+2y0,y1y2=k2x1x2+k(y0-kx0)(x1+x2)+(y0-kx0)2代入上式得:

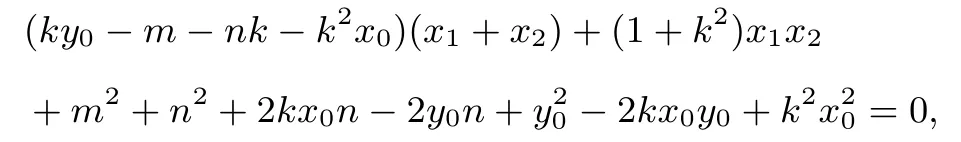
将(1)(2)代入上式整理得:

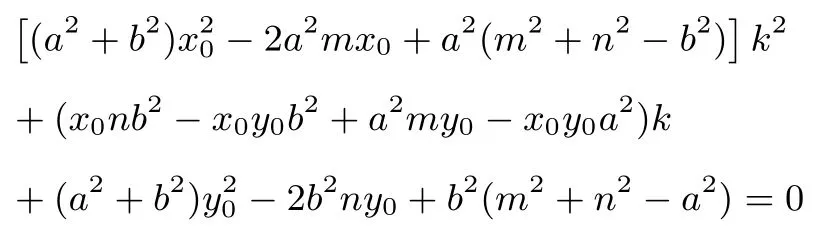
所以当k ∈R 时,上式恒成立.由于T(m,n)是椭圆C上一定点,所以

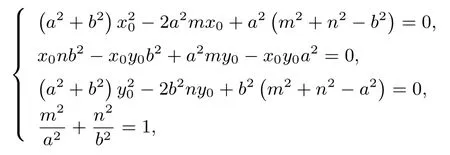
结论3(双曲线情形) 已知O是直角坐标原点,A、B是双曲线C:= 1(a ＞0,b ＞0 且a /=b) 上异于顶点的两动点,T(m,n) 是双曲线C上一定点(m,n为常数), 且TA ⊥TB, 则直线AB过定点

双曲线情形的证明方法与椭圆情形类似.

圆锥曲线的统一性质1已知O是直角坐标原点,A、B是抛物线C:x2=2py(p ＞0)(或椭圆C:=1(a ＞b ＞0)或双曲线C:=1(a ＞0,b ＞0 且a/=b))上异于顶点的两动点,T是抛物线上一定点,且TA ⊥TB,则直线AB过定点.

结论4(抛物线情形)如图4,已知O是直角坐标原点,A、B是抛物线C:x2= 2py(p ＞0) 上异于顶点的两动点,T(2pt,2pt2) 是抛物线C上一定点(t ∈R 为常数), 且TA ⊥TB,TM ⊥AB并与AB相交于点M,则点M在定圆x2+(y-p-2pt2)2=4p2t2+p2上运动.

证明由结论1 可知直线AB过定点Q(-2pt,2p+2pt2).又因为T(2pt,2pt2)也为定点,且TM⊥AB,所以点M在以线段TQ为直径的定圆上运动.圆心为线段TQ中 点(0,p+2pt2), 半径所以点M所在定圆的方程为:x2+(y-p-2pt2)2=4p2t2+p2.证毕.

结论5(椭圆情形) 已知O是直角坐标原点,A、B是椭圆C:= 1(a ＞ b ＞0) 上异于顶点的两动点,T(m,n) 是椭圆C上一定点(m,n为常数), 且TA ⊥ TB,TM ⊥ AB并与AB相交于点M, 则点M在定圆上运动.

结论6(双曲线情形) 已知O是直角坐标原点,A、B是双曲线C:= 1(a ＞0,b ＞0 且a /=b) 上异于顶点的两动点,T(m,n) 是双曲线C上一定点(m,n为常数), 且TA ⊥TB,TM ⊥AB并与AB相交于点M, 则点M在定圆上运动.

结论5、6 的证明方法与结论4 类似.由结论4-6 可得:

圆锥曲线的统一性质2已知O是直角坐标原点,A、B是抛物线C:x2=2py(p ＞0)(或椭圆C:=1(a ＞b ＞0)或双曲线C:= 1(a ＞0,b ＞0 且a /=b))上异于顶点的两动点,T是抛物线上一定点,且TA ⊥TB,TM ⊥AB并与AB相交于点M,则点M在定圆上运动.

结论7(抛物线情形) 如图5, 已知O是直角坐标原点,A、B是抛物线C:x2=2py(p ＞0) 上异于顶点的两动点,T(2pt,2pt2) 是抛物线C上一定点(t ∈R 为常数),且TA ⊥TB,点M是线段AB的中点,则M的轨迹方程是抛物线(x+pt)2=py-2p2-p2t2.

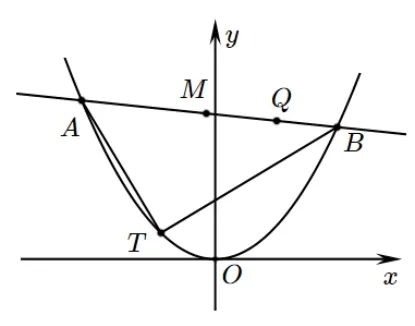
图5

证明设A(x1,y1),B(x2,y2),M(x,y), 直线斜率为k.则两式做差化简得由结论1 可知直线AB过定点Q(-2pt,2p+2pt2),所以

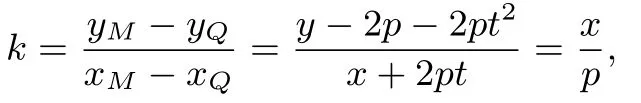
由上式化简整理得(x+pt)2=py-2p2-p2t2.证毕.

结论8(椭圆情形)已知O是直角坐标原点,A、B是椭圆C:= 1 (a ＞b ＞0) 上异于顶点的两动点,T(m,n)是椭圆C上一定点(m,n为常数),且TA ⊥TB,点M是线段AB的中点,则M的轨迹方程是椭圆

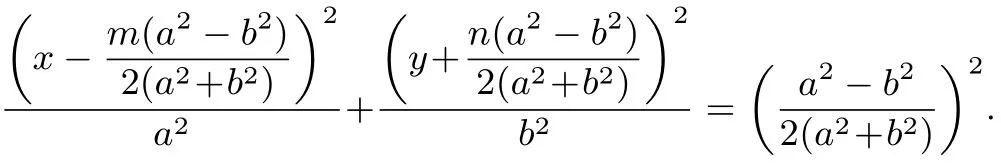
结论9(双曲线情形)已知O是直角坐标原点,A、B是双曲线C:=1(a ＞0,b ＞0 且a/=b)上异于顶点的两动点,T(m,n)是双曲线C上一定点(m,n为常数),且TA ⊥TB,点M是线段AB的中点,则M的轨迹方程是双曲线

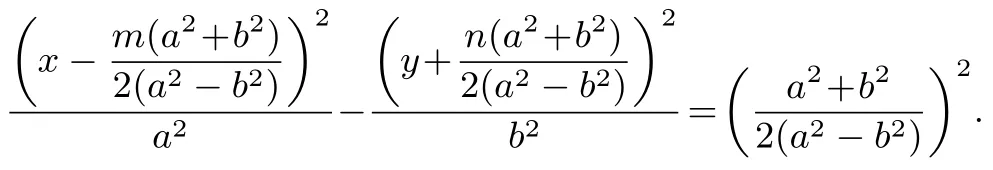
结论8、9 的证明方法与结论7 类似.由结论7-9 可得:

圆锥曲线的统一性质3已知O是直角坐标原点,A、B是抛物线C:x2=2py(p ＞0)(或椭圆C:b ＞0)或双曲线C:=1(a ＞0,b ＞0 且a/=b))上异于顶点的两动点,T是抛物线上一定点,且TA ⊥TB,点M是线段AB的中点,则M的轨迹仍是抛物线(或椭圆或双曲线).

结论10(抛物线情形)如图6, 已知O是直角坐标原点,A、B是抛物线C:x2=2py(p ＞0) 上异于顶点的两动点,T(2pt,2pt2) 是抛物线C上一定点(t ∈R 为常数),

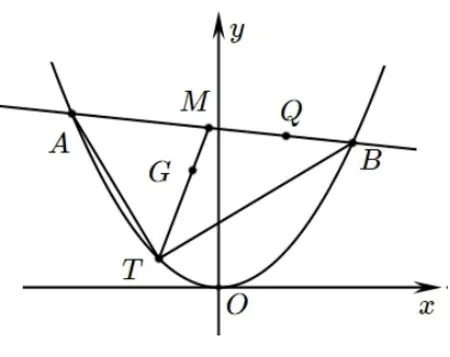
图6

且TA ⊥TB,点M是线段AB的中点,点G是ΔTAB的重心,则重心G的轨迹方程是抛物线: 9x2=6py-8p2-8p2t2.

证明设M(x0,y0),G(x,y).则=(2pt-x,2pt2-y)并且= (2pt - x0,2pt2- y0).由重心的性质知所以

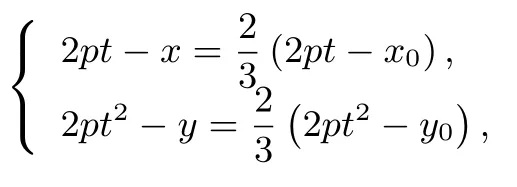
化简得

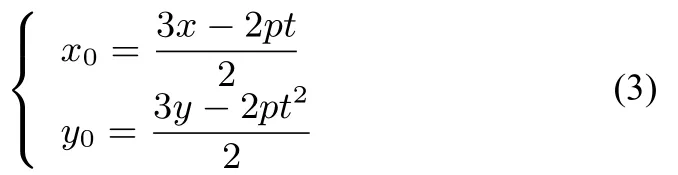
由结论7 知:M点满足(x0+pt)2=py0-2p2-p2t2.将(3)代入上式化简整理得: 9x2=6py-8p2-8p2t2.证毕.

结论11(椭圆情形)已知O是直角坐标原点,A、B是椭圆C:= 1 (a ＞b ＞0)上异于顶点的两动点,T(m,n)是椭圆C上一定点(m,n为常数),且TA ⊥TB,点M是线段AB的中点,点G是ΔTAB的重心,则重心G的轨迹方程是椭圆:

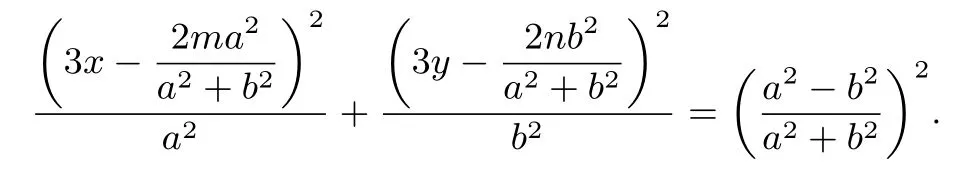
结论12(双曲线情形)已知O是直角坐标原点,A、B是双曲线C:= 1(a ＞0,b ＞0 且a /=b)上异于顶点的两动点,T(m,n)是双曲线C上一定点(m,n为常数),且TA ⊥TB,点M是线段AB的中点,点G是ΔTAB的重心,则重心G的轨迹方程是双曲线:

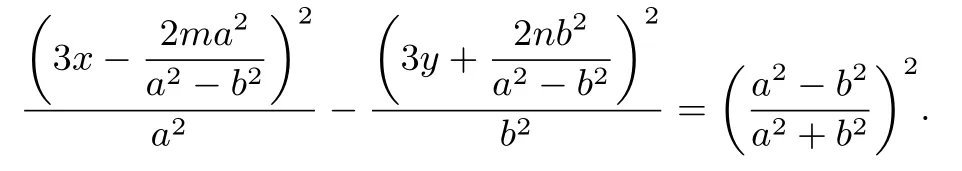
结论11、12 的证明方法与结论10 类似.由结论10-12 可得:

圆锥曲线的统一性质4已知O是直角坐标原点,A、B是抛物线C:x2= 2py(p ＞0)(或椭圆C:1 (a ＞b ＞0) 或双曲线C:= 1 (a ＞0,b ＞0且a /=b))上异于顶点的两动点,T是抛物线上一定点, 且TA ⊥TB,点M是线段AB的中点,点G是ΔTAB的重心,则重心G的轨迹仍是抛物线(或椭圆或双曲线).

3 问题的总结

课本例题、习题既是知识应用的典型,也是思维训练的范例.从往届的高考试题的命制来看,课本例题、习题往往是其最大的知识生长点之一.通过对课本习题多角度、全方位的深入探究,不仅可以加深学生对数学概念、法则、定理等基础知识的理解和掌握,更能够提升学生发现问题、提出问题、分析问题、解决问题的能力,对开发学生的智力,培养学生的数学思维,提升学生的核心素养具有积极重大的意义[1].