基于MKECA的离心铸造过程炉管故障监测方法研究
2021-05-12苑保利林其钊蔡振宇
苑保利 ,林其钊,蔡振宇
(1.中国科学技术大学 能源动力,安徽 合肥 230000; 2.合肥美的电冰箱有限公司,安徽 合肥 230000)
在我国机械加工、精炼生产过程中,工业炉作为主要的能源供 应设备,其重要性是显而易见的。但由于技术、设备等原因,国内多数炼化公司对工业炉的燃烧监测一直处于人工监控且不安全的阶段。与国外一些发达地区相比,在燃烧监控系统的研究与推广应用方面,我国差距较大。
近年来,在安全、效率和环境保护方面,国家对主要炼化公司的要求一直在提高,并且对人力和财力的投资逐年加大。同时,一些国内燃烧监测设备制造商也在逐年增多,技术与设备越来越精细化与复杂化,过去只能靠进口的火焰监测和控制设备,现能实现国产化,且更精良,可以极大提高炼化企业监控水平。这一切,都为我国石化行业全面提升工业炉燃烧监测及控制水平,保障炼化企业的安全生产,实现节能降耗提供了有利条件[1]。于兴智[2]提出利用远程监控及计算机图像识别技术实现对排放黑烟进行自动监测,但这一方法无法确定烟气含量与黑度两者之间的对应关系,且需依靠人来判断颗粒物排放浓度,会引入人为误差。刘玲玲[3]提出基于WinCC的工业炉群智能监控系统,集中了智能化、信息化、网络化等先进技术,但该方法涉及的系统较复杂,无法广泛、短时间推广。冯素梅[4]提出利用主元分析(Principal Component Analysis,简称PCA)构建炉管故障监测模型,PCA方法是一种成熟有效、数据处理方法,构建的监测模型构建较简单,实用性较强,但PCA提取特征值波动性大,诊断结果不准确[5]。
针对以上方法的不足之处,本文提出一种基于多向核熵成分分析(Multiway Kernel Entropy Component Analysis,简称MKECA)的故障监测方法,应用于工业炉管的离心铸造过程。首先,将离心铸造过程三维数据进行数据预处理,利用沿批次-变量展开方法,将三维数据转换成二维数据,再将正常批次的二维数据带入MKECA监测模型内计算正常批次下的角结构相似度统计量,统计量控制限利用核密度估计值算法获得,本文选取99%的置信区间,最后将实时数据进行数据预处理后,代入模型内进行炉管故障监测。本文通过对乙烯裂解炉管实际生产数据进行分析实验和各种对比研究,验证了该方法的有效性。
1 离心铸造过程
1.1 离心铸造过程简介
离心铸造过程的定义是将熔融金属液体注入到高速旋转的模具型筒内,且在离心力的作用下填充并固化液态金属的一种铸造方法[6]。离心铸造工业主要包括6个部件,由图1可以看出整个工作原理与各个部件位置。
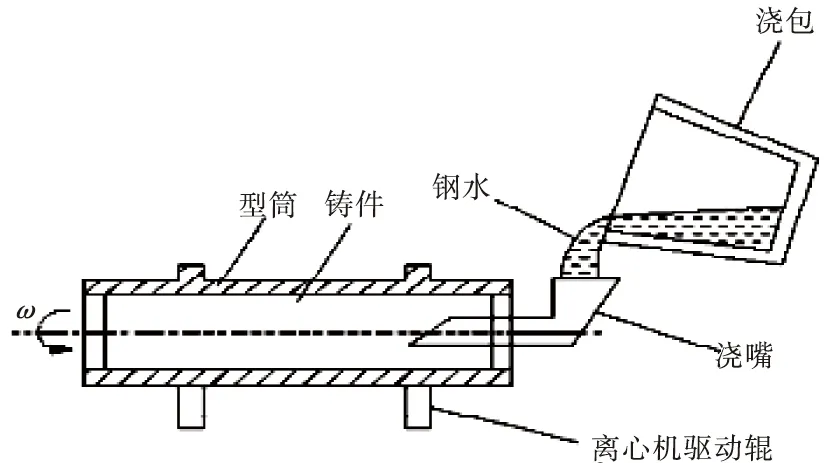
图1 离心铸造过程
1.2 离心铸造过程的变量特征
工业炉生产过程主体由原料熔融与离心铸造两大部分构成。原料熔融阶段,该过程是将原材料熔融,主要是为了获得合格的钢水,用于浇铸。钢水中含有多种化学元素,比如C、Si、Mn、P、S、Cr、Ni、W、Nb、Mo、Cu、Al、Fe。
离心铸造工业过程是工业炉第二大组成部分,该过程存在批次、时间、变量三个维度数据,与其他间歇工业工程类似,是一个复杂的工业过程,每个工业炉管的铸造过程可视为一个批次,每个工业炉管随时间迁移,特征变量也会随之变化,批次、时间、变量三者之间都有复杂的联系。本文参考文献[4],选取工业炉离心铸造工业过程中的变量如表1所示。

表1 离心铸造过程监测变量
1.3 离心铸造过程三维数据处理
针对上节所述,离心铸造过程表现为三维数据,其中,I为批量数,J为变量数,K为采样点数(时间点),比普通连续工业过程的数据多出一维批次数据,数据结构更加复杂。三维数据向二维扩展,常用的两种方法:沿批量和变量扩展,其中沿批次方向展开原理图如图2所示。
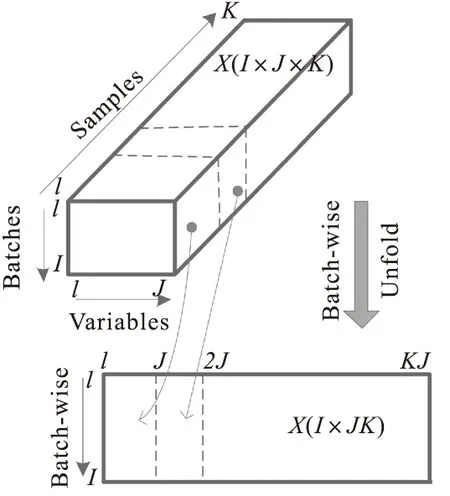
图2 沿批次数据展开
沿批次方向展开的主要优点是,在对数据集列向矩阵进行标准化后,能突出显示每个批次的变化信息,提取该过程变量的平均轨迹,并且消除或减弱非线性的影响。主要缺点是,在监视故障时,各批次数据需要完整,每个批次数据长度一致,当进行故障监测时需要估计从当前采样点到批次结束的数据值,该过程预估值与实际值会存在一定误差,预估值较少,误差可以忽略不计,但预估数值较多时,整个监测结果误差较大。沿变量方向展开原理如图3所示,该方法的优点是无需考虑批次数据长度一致性,对监测采样数据也无需填补成一个完整的批次,但缺点无法突出批次之间的关系与差异,且该方法无法消除或减弱时间变量上的非线性,故对故障敏感程度低,从而实现的故障监测效果较差。
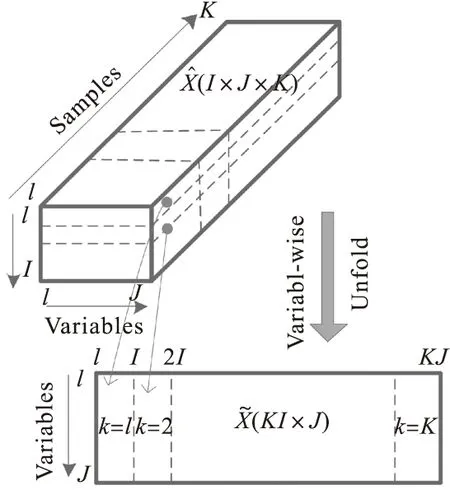
图3 沿变量数据展开
针对上述两种三维数据预处理的不足,本文引用文献[7]所提的方法,将三维数据沿批次-变量展开,展开原理图如图4所示。将三维数据,先沿批次方向展开,再按变量方向展开,沿批次展开可以突出批次信息,沿变量展开无需考虑完整批次数据,可以综合前两者优点,弥补两者缺陷,能有效的提取数据信息,为构建高效的故障监测模型打好良好的数据基础。

图4 沿批次-变量数据展开
2 基于MKECA离心铸造过程故障监测
2.1 KECA理论
KECA与KPCA选取特征数据不同在于,KECA通过Renyi熵大小来选取特征信息。假设某一概率问题中有n个事件,第i个事件Xi产生的概率为Pi(i=1,2…,n),则时间转换成Renyi熵指标的公式为
(1)
式(1)对数函数属于单调函数,在取值范围内单增或单减。因此可以单独分析积分部分,对积分部分进行单独定义,公式如下:
(2)
V(p)是对概率值的平方求积分,需计算出具体值才能确定Renyi熵值,本文引入Parzen概率密度算子[8],根据高斯函数卷积理论,再结合函数的单调性,可以将公式化简得到
(3)
(4)
式中:I表示矩阵内所有元素均为1的N维向量;K为样本核矩阵。
通过式(5)可以实现Renyi熵的核矩阵表达,该矩阵分解公式表示为
K=EDλET
(5)
式中:Dλ为特征值λ1,…,λn组成的对角矩阵;E则为由特征向量e1,…,en组成的矩阵。
因此,式(3)进一步可表示为
(6)
式中:1为n×1的向量,式(6)可以表示为每个特征值,和特征值对应的特征向量对Renyi熵产生不同的贡献,得到的转换数据:
(7)
式中:Φeca为KECA映射;D是特征值为λ1,λ2,…,λn的对角矩阵;E=[e1,e2,…en]。
2.2 角结构相似度统计量
由于采样数据经过KECA转换后,数据信息内有较好的角结构信息,因此本文引入一种新型故障监测统计量-角结构相似度统计量CV,用于故障监控,定义如下[9]:
(8)
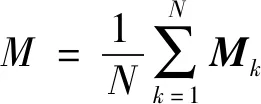
角结构相似度统计量CV是计算矩阵与矩阵之间的相似度,对比矩阵则是其他矩阵的平均值。相似度越高,CV值就越高,但为在图纸和结果表现更直观,将该数据值用1减去相似度值得到统计量值。因此在正常批次数据下,数据与原历史数据相似度高,就会低于控制限,反之就会高于控制限,表示为故障,可以实现高效故障监测。为避免选取控制限方法而引入的误差,本文采用核密度估计计算CV统计量的控制限(CK),该方法在计算控制限时,无须假设数据遵从高斯分布,数据处理更加偏于实际生产。
3 实验分析与讨论
3.1 实验数据来源
为验证本文提出方法的有效性,共收集到32根实际工业炉生产的炉管数据,其中24根合格,8根不合格。本文实验分析主要从两部分分析,一是主元个数选取,二是整体监测效果对比。为对比本文提出方法的有效性,两部分都引入MKPCA方法作对比实验。
3.2 主元个数选择MKECA与MKPCA对比分析
在构建MKECA故障监测模型时,数据主元个数的选取与监测效果有很大关系。数据主元选取过多,数据处理时间长,虚假、杂质信息过多,影响监测效果;主元个数过少,故障特征信息表现少,削弱故障表现能力,也会影响监测效果,因此故障监测效果与MKECA处理后的主元个数选取至关重要。本文将正常三维数据预处理成二维数据后,代入MKECA监测模型内,获得该模型不同主元个数下的控制限和原始数据矩阵,再将预处理后的验证数据代入监测模型内,计算在不同主元个数模型下,各个监测模型的诊断率和误报率,本文规定误报率为合格炉管被误诊出故障的概率,诊断率为不合格炉管被诊断出故障的概率。该过程验证的合格数据和故障数据都是同一组,为对比研究,本文增加MKPCA进行对比验证。表2和图5列出了验证数据在不同主元个数时,MKECA与MKPCA两种监测模型误报率诊断率的结果。
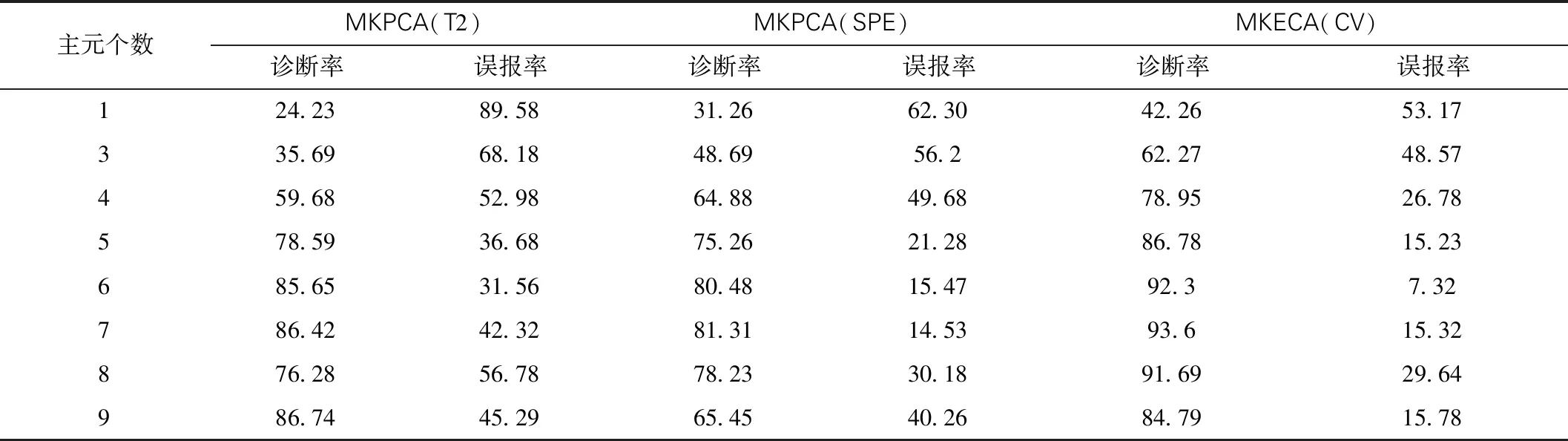
表2 验证数据选择主元个数的结果 %

图5 MKECA主元选取个数诊断率与误报率结果图
由表2数据可以看出,在MKPCA数据结果中,统计量T2在主元个数为6个时,效果最佳,误报率在同模型下也最低,SPE的统计量在主元个数为7时综合检测效果最好,但MKPCA是综合T2与SPE两种统计量来算,因此综合两者分析,主元个数为6,效果最佳;相比MKPCA,MKECA监测效果由图5可以看出,虽然当主元个数为7时,诊断率最高,但是综合误报率来看,主元个数为6时,MKECA的CV统计量监测效果最好,因此当取主元个数为6时,整体故障监测效果最佳,构建的该模型效果最好。
3.3 MKECA与MKPCA故障监测对比研究
为研究MKECA在离心铸造过程中的故障监测能力,利用16组正常数据构建MKECA离线监测模型,再将8组合格数据集与8组故障数据集代入构建好的故障监测模型内,实现在线故障监测误报率和故障诊断率。为对比研究本文提出方法的有效性,利用MKPCA进行对比,两种模型的主元个数都选6。
表3和图6~图11是取99%的置信区间取CV、T2和SPE的控制限,表2是8组合格与8组故障数据的整体监测效果,从数据中可以看出,MKECA误报率为6.75%,误报率相比MKPCA的T2与SPE效果最低,说明MKECA的误报最少,效果最好,反之诊断率须越高越好,MKECA的CV诊断率整体效果最高,说明识别故障效率最好,因此验证了MKECA统计监测效果最好,验证了该方法的有效性。图6~图11展现的是某个合格批次和不合格批次误报率、合格率效果图,从图6~图11可以直观看出MKECA的监测效果更佳。

图11 某不合格数据集MKPCA诊断率SPE效果图

表3 故障监测误报率与故障诊断率对比 %

图6 某合格数据集MKECA误报率效果图
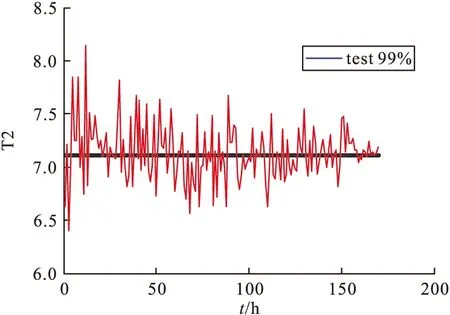
图7 某合格数据集MKPCA误报率T2效果图
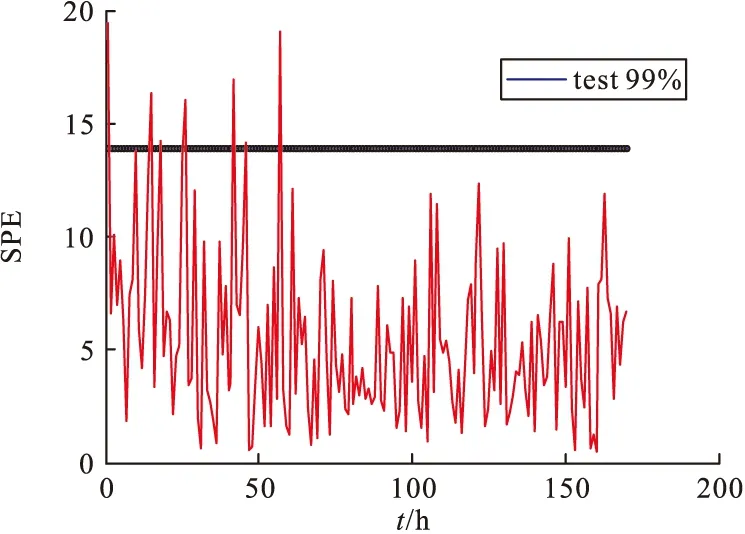
图8 某合格数据集MKPCA误报率SPE效果图
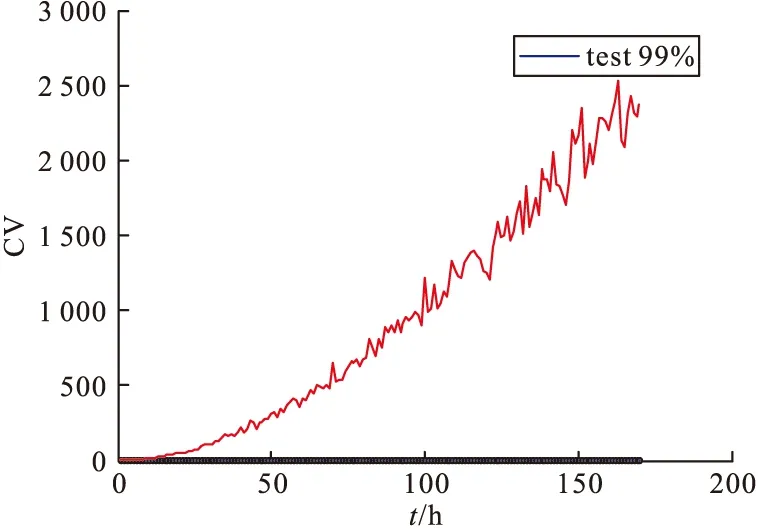
图9 某不合格数据集MKECA诊断率CV效果图
4 结 论
针对目前离心铸造工业炉管生产过程监控方法复杂、耗费高等特点,本文提出基于MKECA进行离心铸造过程故障监测方法。工业炉管的离心铸造过程是一种间歇工业过程,间歇过程表现是三维数据集,首先将三维数据集沿批次-变量二维数据展开,再利用MKECA建立离线故障监测模型,得到CV控制限和历史正常矩阵数据,再代入验证数据计算验证数据的CV统计量,判断是否超出控制限,以此方法进行故障监测。本文利用乙烯裂解炉管实际生产过程数据,代入MKPCA监测模型内与本文提出的MKECA监测模型进行对比验证,从结果来看,本文的方法误报率6.75%,故障诊断率是94.53%,远高于MKPCA的方法,验证了该方法的有效性与可行性,为实际生产提供一条可行的故障监测思路。
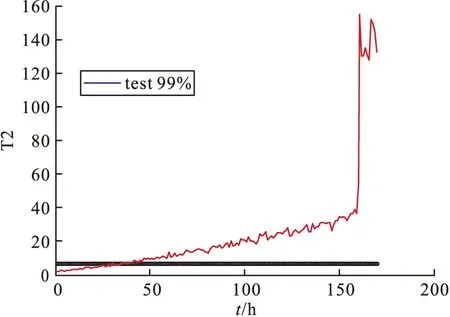
图10 某不合格数据集MKPCA诊断率T2效果图
