基于多尺度行波功率的T接线路故障识别方法

2021-05-11胡潇涛顾小平陈佳豪

电力系统及其自动化学报 2021年4期

杨杰，吴浩，2，胡潇涛，顾小平，陈佳豪

（1.四川轻化工大学自动化与信息工程学院，自贡 643000；2.人工智能四川省重点实验室，自贡 643000）

随着社会经济的不断发展，以及对电能需求的日益增加，电网变得越来越复杂。从节约投资以及其他客观条件限制等方面考虑，T接线路因其接线方式的独特性，在高压和超高压电网中得到广泛应用。然而，T接线路常常伴随着大电厂和大系统，线路传输功率高，当线路发生故障时，有可能造成大面积停电事故。因此，为防止事故扩大，减小因停电而造成的经济损失，要求能快速准确地诊断故障[1-6]和排除故障。

目前，国内外学者对T接线路故障识别的研究主要是基于工频或暂态故障信息建立判据，识别区内外故障。文献[7]利用T接线路三端电压故障分量相量和与电流故障分量相量和的比值大小，识别区内外故障。文献[8]利用T接线路三端电流故障分量之和以及三端电流故障分量中的最大电流与另外两端电流之和的矢量差建立判据，识别区内外故障，但判据中制动系数的选取会对故障识别的灵敏性和可靠性造成影响。文献[9]针对文献[8]中存在的问题，利用T接线路三端故障电流分量中最大电流结合另外两端电流矢量之和及其余弦夹角建立判据，识别区内外故障。文献[10]根据文献[8-9]中的判据建立综合判据，实现光伏T接高压配电网络区内外故障的识别，但未对算法性能进行分析。文献[11]通过比较T节点正序电压叠加分量的最大幅值与三端正序电压叠加分量的最大幅值关系，识别区内外故障。文献[12]利用T接线路三侧电压幅值差和测量阻抗特征建立的综合电压幅值差作为主判据，结合自适应距离辅助判据识别区内外故障。文献[13]利用T接线路三端暂态电流的余弦相似度建立判据，识别区内外故障。在传统T接线路故障识别研究中，T接线路故障识别算法仅能识别区内外故障，不能识别具体的故障支路，而且部分算法故障识别准确度易受其他变量影响。在算法性能分析方面，传统算法大都未对故障识别性能进行进一步研究。

近年来，学者们广泛研究怎样把神经网络应用于电力系统故障诊断中，但神经网络用于T接线路故障诊断方面的研究还比较少。为克服传统T接线路故障识别算法的不足，本文借鉴文献[14-16]的研究思路，利用多尺度平均行波有功功率表征T接线路故障特征，结合神经网络强大的模式识别能力，提出了一种基于多尺度行波有功功率和概率神经网络的T接输电线路故障识别新算法。该算法利用S变换后T接线路区内三端行波保护单元的初始电压和电流行波，计算多个S变换频率下的行波平均有功功率，并将其组成T接线路故障特征向量样本集，结合概率神经网络PNN（probabilistic neural network）故障智能识别模型进行训练与测试，识别T接线路故障所在支路。仿真结果表明，所提算法在各种工况下均能快速准确地识别T接输电线路区内外故障所在支路。

1 故障初始行波功率分析

1.1 故障行波的基本理论

图1为500 kV的T接线路，由区内支路AO、BO、CO和区外支路AD、BE、CF组成，行波保护单元TR1～TR3分别安装在区内支路靠近A、B、C 3端母线处。当故障发生在区内AO支路F1处时，行波沿线路从故障点向两侧传播，在线路波阻抗不连续处发生折反射[17]。

图1 500 kV的T接线路Fig.1 500 kV T-connection transmission line

根据行波传播理论，设t0m分别为初始行波首次到达A、B、C 3端的时刻，t1m为行波在线路波阻抗不连续处发生折反射后第2次到达A、B、C 3端的时刻，m=1,2,3；在t0m～t1m时段内，区内支路近A、B、C 3端处的行波保护单元TRm获取的故障行波分别称为初始电压行波Δum和初始电流行波Δim。

1.2 故障初始行波功率分布

1.2.1 区内故障时初始行波功率分布

设电流方向流出母线为正，流进母线为负，功率可根据各母线关联线路电流方向定义正或负。

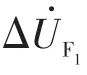
图2 T接线路区内支路OA故障时彼得逊等效电路Fig.2 Peterson equivalent circuit under fault in internal branch OA of T-connection transmission line

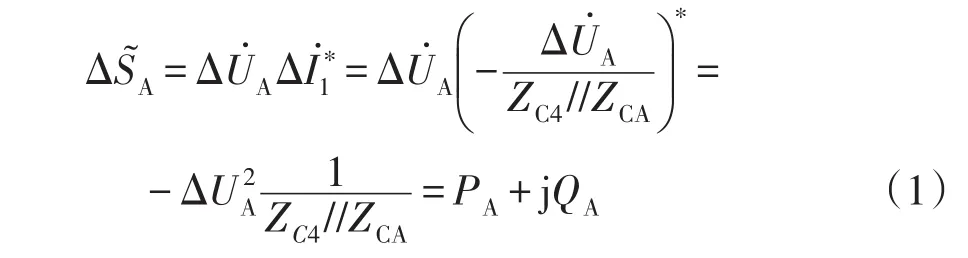
式中：PA为线路初始行波有功功率；QA为线路初始行波无功功率。

当T接线路区内故障时，PA可表示为

1.2.2 区外故障时初始行波功率分布

当故障发生在T接线路区外AD支路F2处时，T接线路的彼得逊等值电路如图3所示。

图3 T接线路区外支路AD故障时彼得逊等效电路Fig.3 Peterson equivalent circuit under fault in external branch AD of T-connection transmission line

由等效电路可得，行波保护单元TR1的复功率为

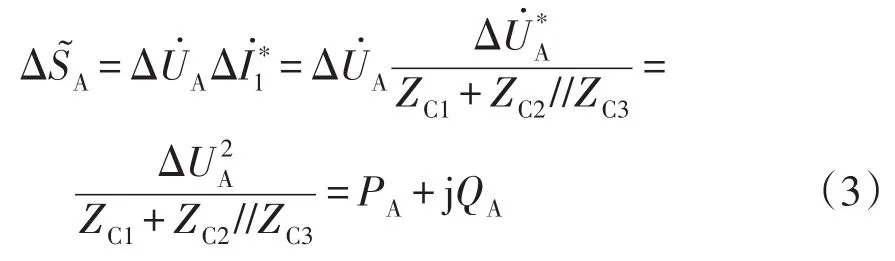
当T接线路区外故障时，PA可表示为

2 基于S变换计算初始行波有功功率

在三相输电系统中，各相电压和相电流之间的耦合会对电压电流造成影响，因此需要对相电压和相电流进行解耦处理，本文采用Clarke变换，对相电压和相电流进行解耦处理，再利用组合模量法来反映T接线路的各种故障类型[16]。解耦处理后的模量电压Δuz和模量电流Δiz可分别表示为

式中：Δuα、Δuβ分别为模电压的α、β分量；Δiα、Δiβ分别为模电流的α、β分量。

本文采用文献[19]所用方法，将对解耦后的故障电流、电压行波模量进行离散S变换，选取故障后多个频率下的电流、电压初始行波波头附近的采样点信息计算初始行波有功功率。

对信号进行S变换后得到1个反映该信号时频特性的复矩阵，矩阵的行对应行波在离散S变换后的频率信息，矩阵的列对应行波时域下各采样时间点的幅值信息和相位信息[19-21]。

2.1 S变换初始行波有功功率

以第m个行波保护单元TRm的某一特定频率fn对应的有功功率计算为例，具体步骤如下。

步骤1对行波保护单元TRm测得的初始电压、电流行波分别进行S变换，得到初始电压、电流行波的复时频矩阵，分别记作SVm、SIm矩阵。

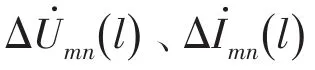
步骤3求取频率fn下各采样点对应的复功率ΔSmn(l)为

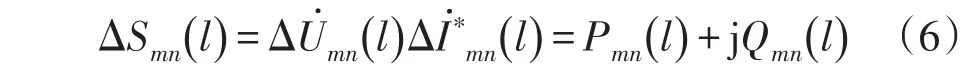
步骤4计算各行波保护单元TRm在频率fn下20个采样点的平均有功功率Pmn为

2.2 T接线路区内外故障初始行波有功功率分析

2.2.1 区内故障初始行波有功功率分析

设置T接线路区内BO支路距O点155 km处发生AC相接地故障，故障初始角为60°，过渡电阻为300 Ω。以S变换后频率为20 kHz对应的信号为例，各行波保护单元TRm相关波形分别如图4～6所示，其中Δim、Δum分别为行波保护单元TRm的初始电流、电压行波，Pm为行波保护单元TRm的初始行波有功功率。

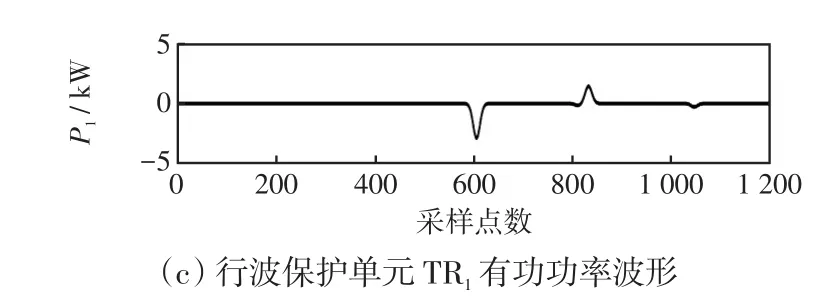
图4 区内BO支路故障时行波保护单元TR1相关波形Fig.4 Corresponding waveforms of traveling wave protection unitTR1under fault in internal branch BO

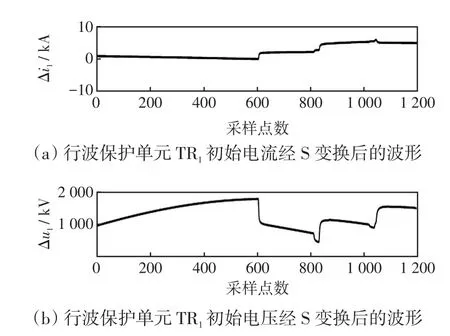
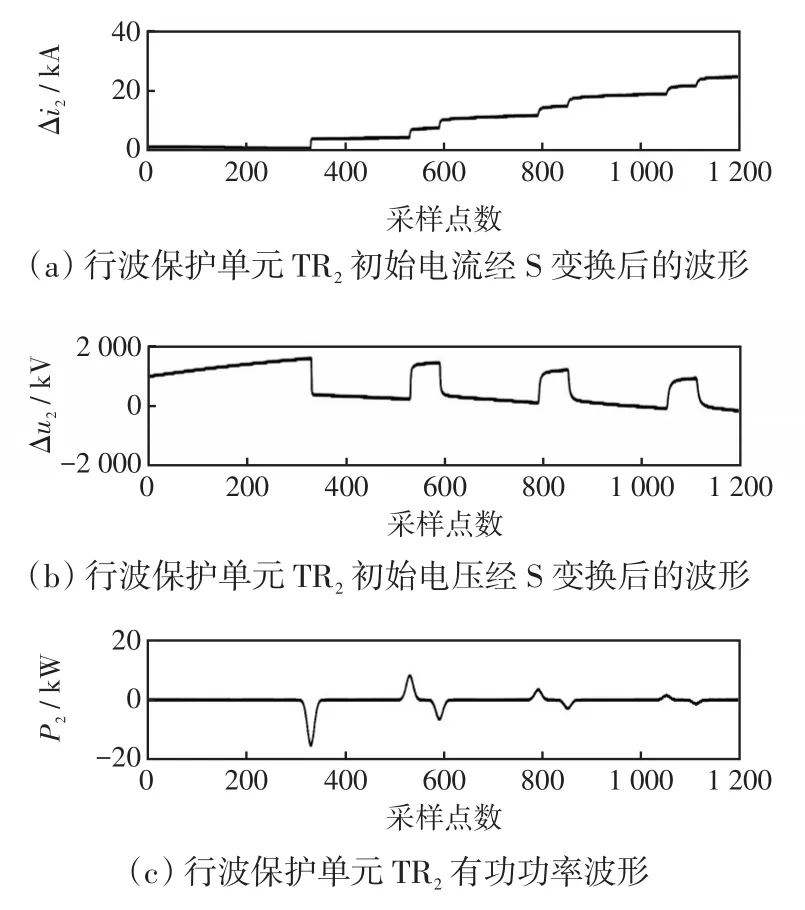
图5 区内BO支路故障时行波保护单元TR2相关波形Fig.5 Corresponding waveforms of traveling wave protection unitTR2under fault in internal branch BO

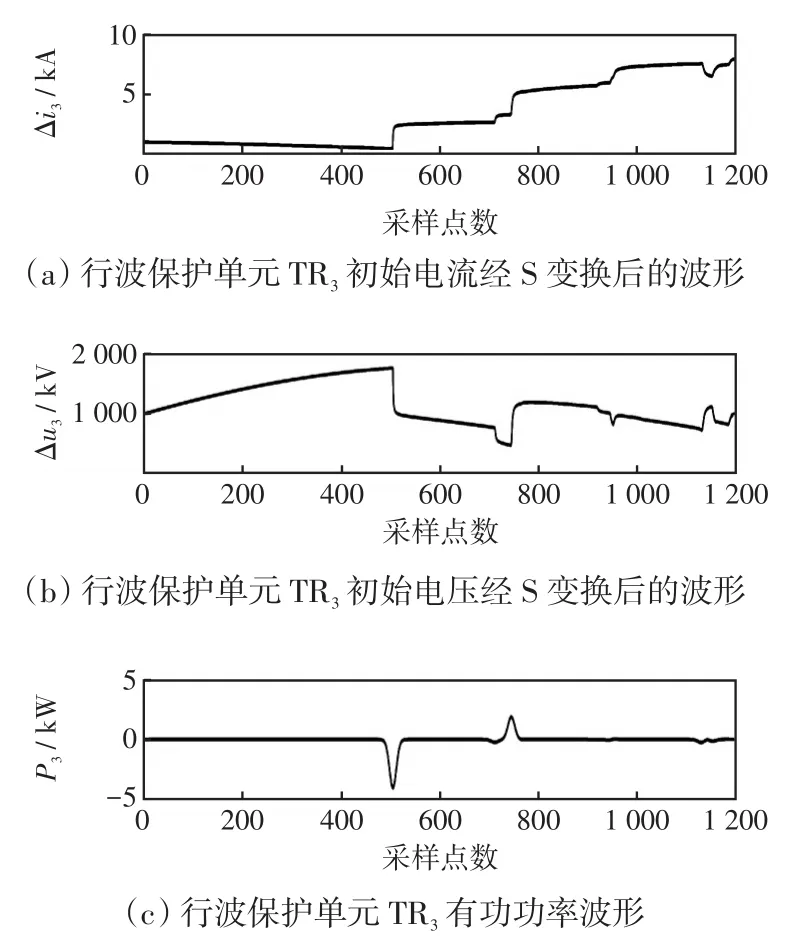
图6 区内BO支路故障时行波保护单元TR3相关波形Fig.6 Corresponding waveforms of traveling wave protection unitTR3under fault in internal branch BO

由图4～6可知，当T接线路区内支路BO发生故障时，根据各行波保护单元初始电压、电流行波波头附近数据所求的有功功率均为负值。

2.2.2 区外故障初始行波有功功率分析

设置T接线路区外支路BE距O点270 km处发生AB相接地故障，故障初始角为45°，过渡电阻为200 Ω。以S变换后频率为20 kHz对应的信号为例，各行波保护单元TRm的相关波形分别如图7～9所示。

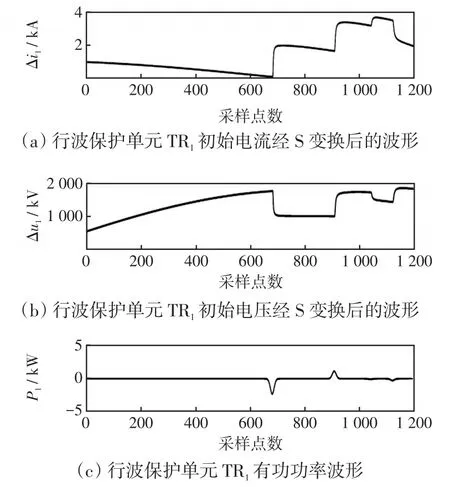
图7 区外BE支路故障时行波保护单元TR1相关波形Fig.7 Corresponding waveforms of traveling wave protection unitTR1under fault in external branch BE

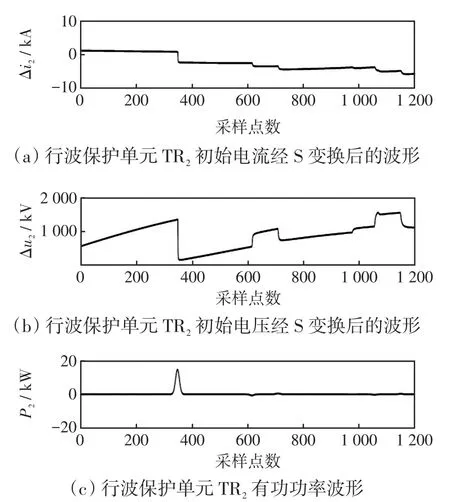
图8 区外BE支路故障时行波保护单元TR2相关波形Fig.8 Corresponding waveforms of traveling wave protection unitTR2under fault in external branch BE

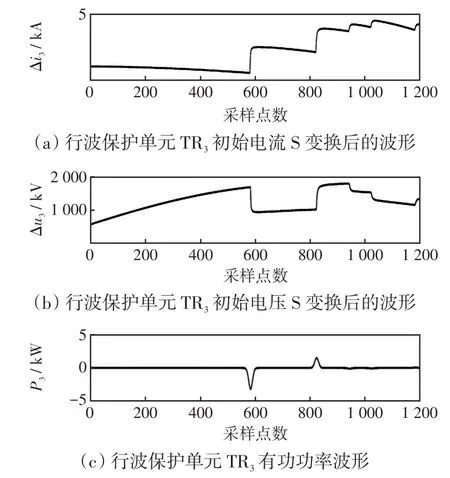
图9 区外BE支路故障时行波保护单元TR3相关波形Fig.9 Corresponding waveforms of traveling wave protection unitTR3under faut in external branch BE

由图7～9可知，当T接线路区外支路BE发生故障时，根据行波保护单元TR2初始电压、电流行波波头附近数据所求的有功功率均为正值；根据行波保护单元TR1、TR3初始电压、电流行波波头附近数据所求的有功功率均为负值。

3 PNN理论

PNN是一种结构简单、训练时间短且不易产生局部最优的前馈型神经网络，其理论依据是贝叶斯最小风险准则即贝叶斯决策理论。该网络由输入层、模式层、求和层和输出层组成，其基本网络结构[22]如图10所示。

图10 PNN网络结构Fig.10 Structure of PNN

4 故障识别算法

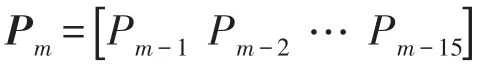
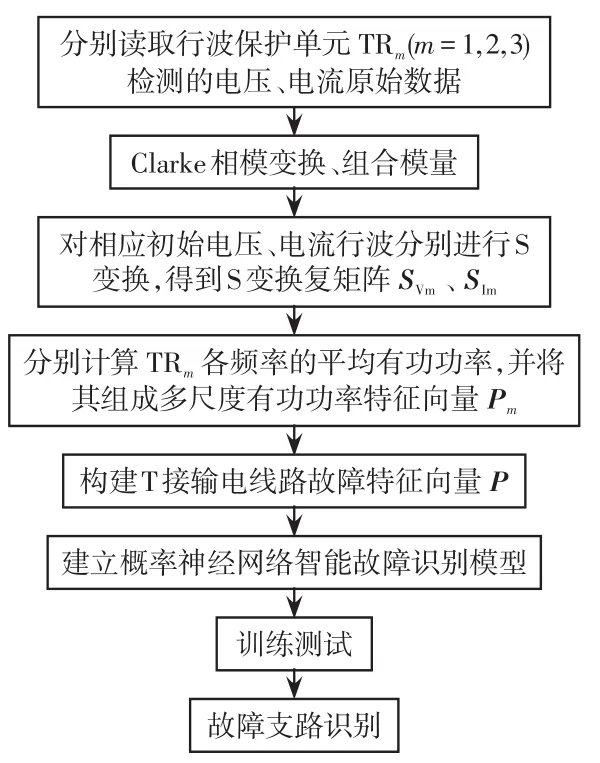
图11 故障支路识别算法流程Fig.11 Flow chart of fault branch identification algorithm

5 仿真与实验

利用PSCAD/EMTDC电磁暂态仿真软件建立图1所示500 kV的T接线路仿真模型，线路模型采用能精确反映暂态和谐波响应的频率相关的分布参数模型，线路型式选用3H5杆塔，输电线配置如图12所示，其中，C为导线，G为地线，输电线路参数如表1和表2所示。母线杂散电容设定为Cm=0.01 μF ，仿真采样频率为200 kHz，各支路长度分别为 AO=300 km，BO=200 km，CO=150 km，AD=170 km，BE=150 km，CF=180 km。

表1 输电线路参数ITab.1 Transmission line parameters I

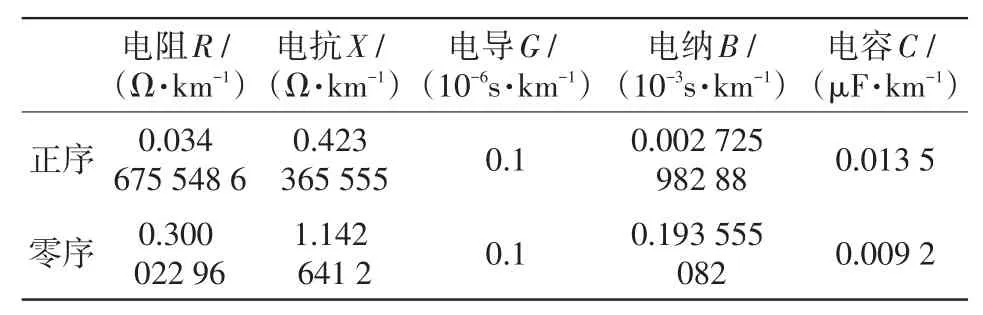
表2 输电线路参数IITab.2 Transmission line parameters II

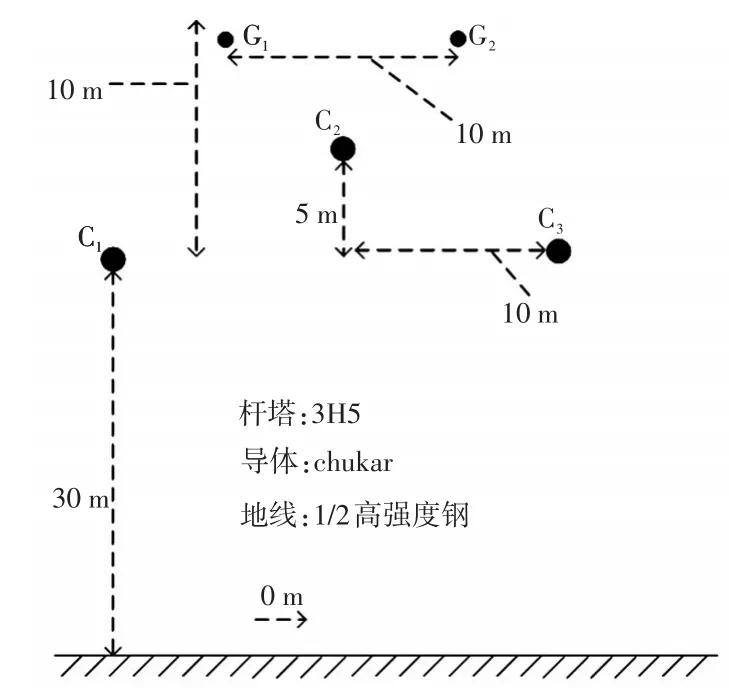
图12 输电线配置Fig.12 Configuration of transmission line

5.1 样本数据

PNN的训练样本由T接线路各支路随机故障样本和区内近O点故障样本2部分组成。

（1）各支路随机故障样本由T接线路区内外6条支路在不同故障初始角、不同过渡电阻、不同故障类型及不同故障距离中4大类各选取5种不同故障情况，仿真得到120组故障特征向量。

（2）区内近O点故障样本是在区内支路AO、BO、CO上分别选取距O点10 km、9 km、8 km、7 km、6 km、5 km、4 km、3 km、2 km、1 km的故障距离，以不同故障条件仿真得到30组故障特征向量。

各支路随机故障样本和区内近O点故障样本共同组成故障特征训练样本集。

5.2 样本实验结果与分析

把故障特征训练样本输入PNN中进行训练，得到1个训练好的T接线路智能故障识别模型。

将故障训练样本输入训练好的PNN模型中测试，得到预测结果与真实值对比如图13所示。由图13可知，训练样本在识别模型中的测试结果正确率均为100%。

图13 训练集预测结果与真实值对比Fig.13 Comparison of prediction results based on training set with true values

5.3 测试样本测试分析

5.3.1 不同故障类型测试

将区内外不同故障类型的故障测试样本输入PNN故障识别模型中测试，预测结果如表3所示，与表3所对应故障情况的预测结果对比如图14所示。由图14与表3可知，当T接线路各支路发生不同类型故障时，算法均能准确识别区内外故障的具体支路，因此所提故障识别算法不受故障类型的影响。

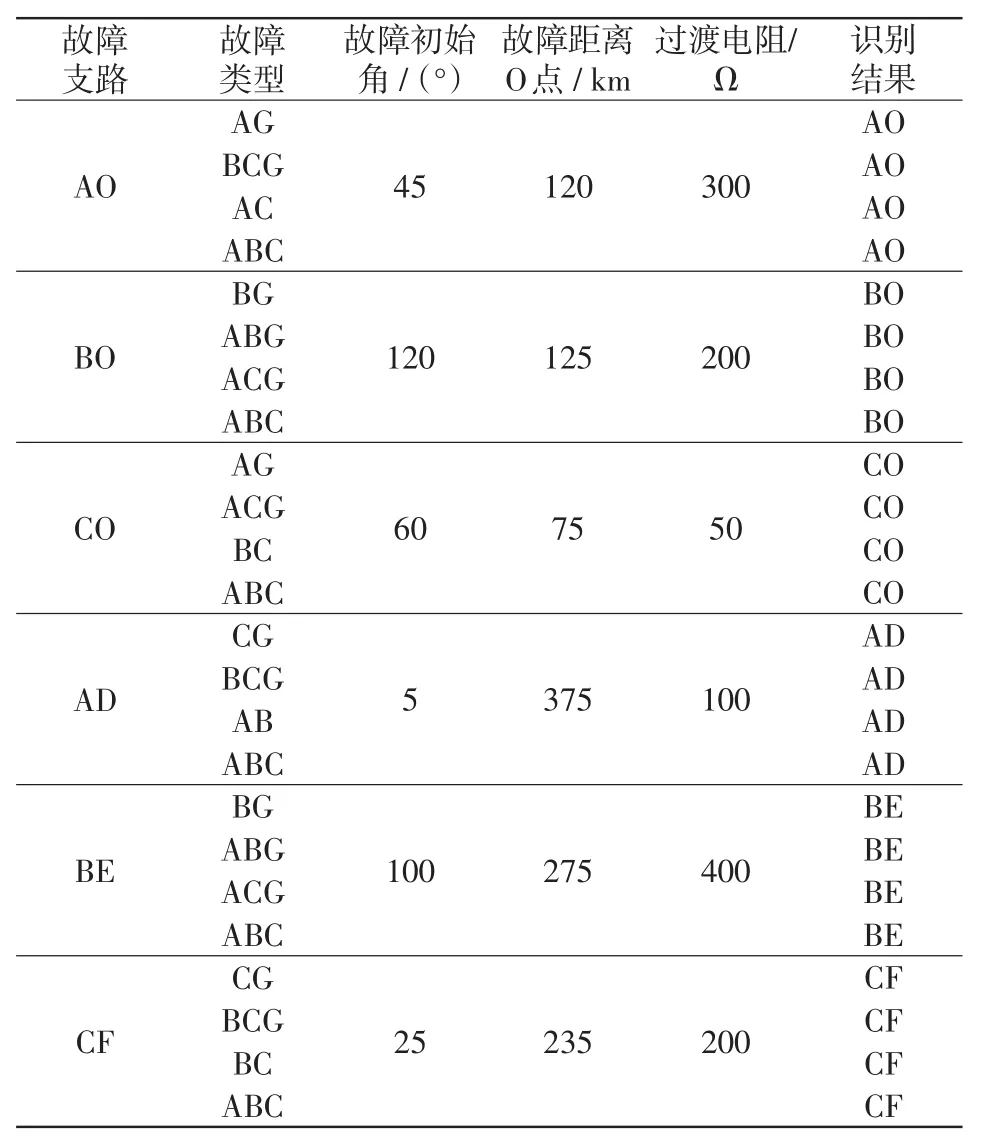
表3 不同故障类型测试集仿真结果Tab.3 Simulation results of test sets of different fault types

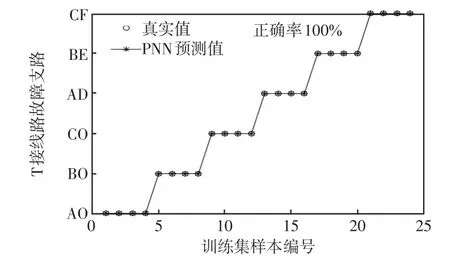
图14 不同故障类型测试集预测结果与真实值对比Fig.14 Comparison of prediction results based on test sets of different fault types with true values

5.3.2 不同过渡电阻测试分析

将区内外不同过渡电阻的故障测试样本输入PNN故障识别模型中测试，预测结果如表4所示。由4表可知，不同过渡电阻故障测试样本在识别模型中测试均能准确识别出故障支路，因此所提故障识别算法不受过渡电阻的影响。

表4 不同过渡电阻故障测试集仿真结果Tab.4 Simulation results of fault test sets with different transition resistances

5.3.3 不同故障距离测试分析

将区内外不同故障距离的故障测试样本输入PNN故障识别模型中测试，预测结果如表5所示。

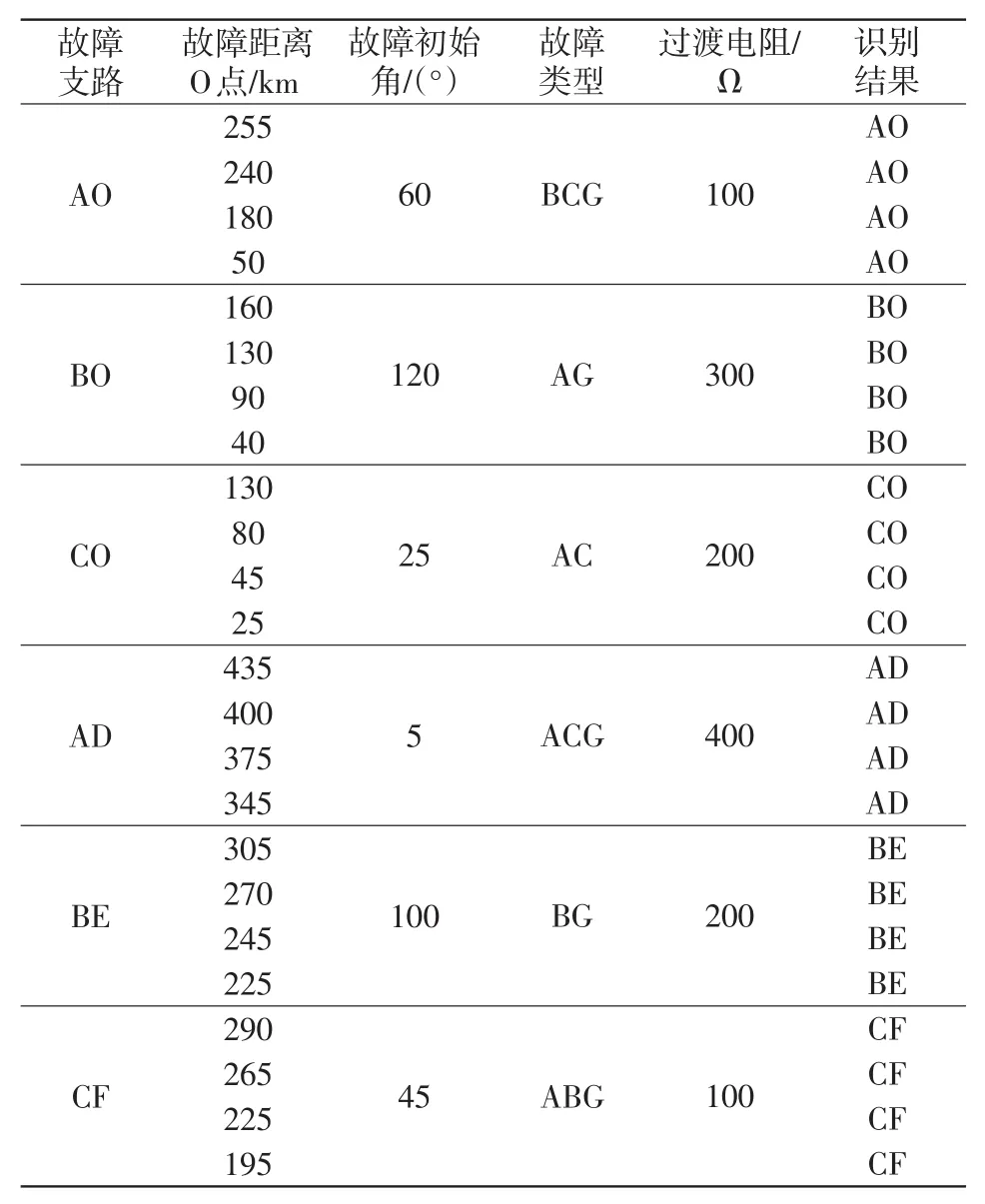
表5 不同故障距离测试集仿真结果Tab.5 Simulation results of test sets with different fault distances

由表5可知，不同故障距离与故障测试样本在识别模型中测试均能准确识别出故障支路，因此所提故障识别算法不受故障距离的影响。

5.3.4 不同故障初始角测试分析

将区内外不同故障初始角的故障测试样本输入PNN故障识别模型中进行测试，预测结果如表6所示。由表6可知，不同初始角故障测试样本在故障识别模型中测试均能准确识别出故障支路，因此所提故障识别算法不受故障初始角的影响。

表6 不同故障初始角测试集仿真结果Tab.6 Simulation results of test sets with different fault initial angles

5.4 故障识别算法性能分析

5.4.1 近O点故障测试样本分析

将O点附近故障时的故障测试样本输入PNN故障识别模型中测试，得到对应故障情况的仿真结果如表7所示。由表7可知，该保护算法能很好地识别T接线路近O点发生故障的支路。

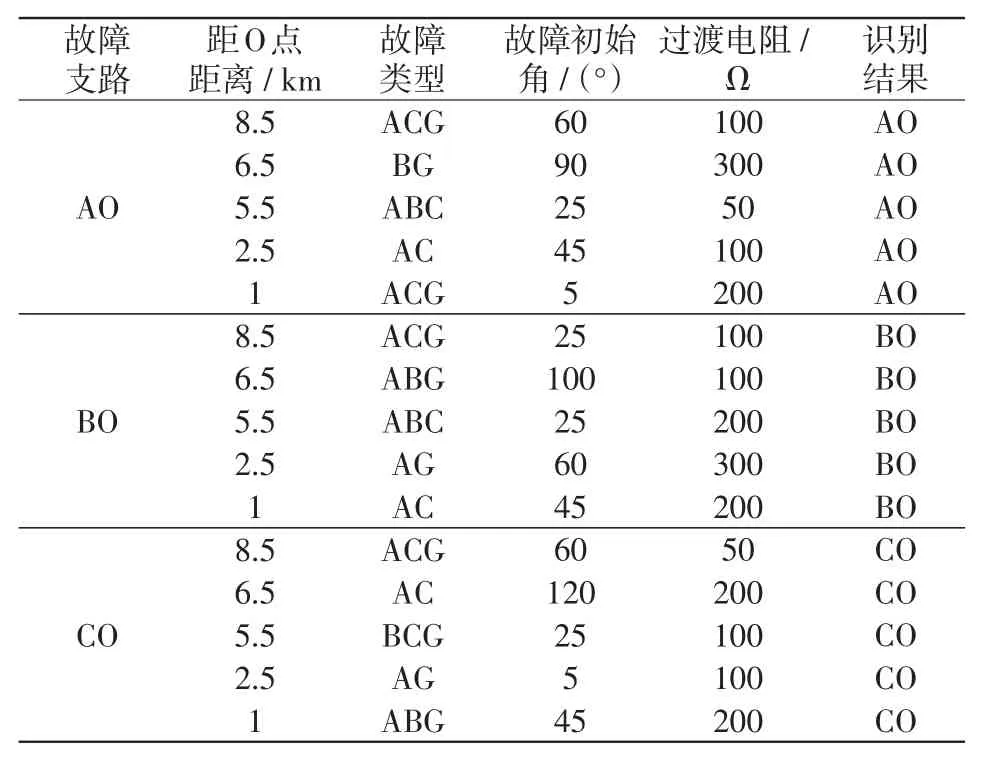
表7 T接线路近O故障测试集仿真结果Tab.7 Simulation results of test sets under fault at the near-O point in T-connection transmission line

5.4.2 数据随机丢失影响分析

保护装置在实际运行中可能出现数据丢失的情况，为验证该情况下的算法性能，以保护单元TR2测量到的初始电流行波数据随机丢失为例，分别选取区内支路BO和区外支路AD进行仿真分析。

以数据窗中随机丢失10个采样点数据为例，图15为区内支路BO在距离O点120 km处发生ABG故障时初始电流行波波头附近数据随机丢失后有功功率分布的相关波形。图16为区外支路AD在距离O点395 km处发生BG故障时初始电流行波波头附近数据随机丢失后有功功率分布的相关波形。

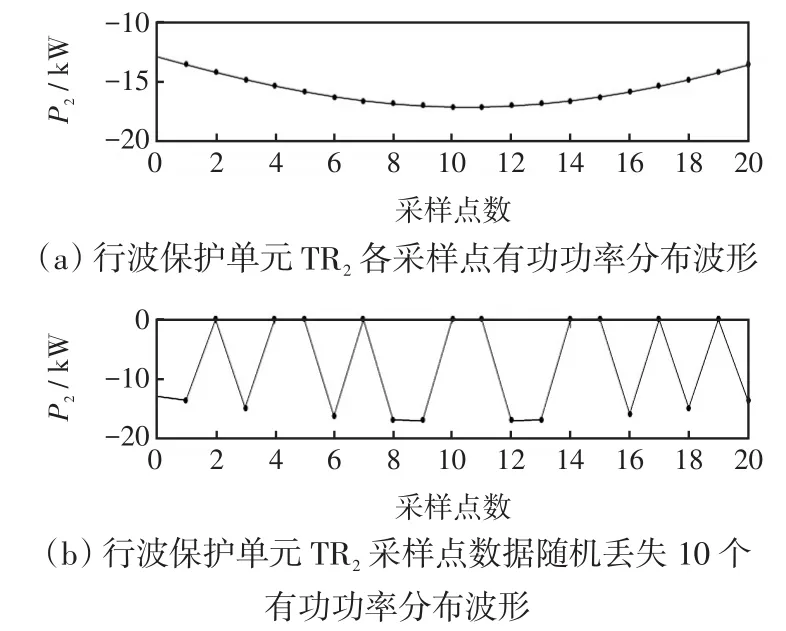
图15 BO支路故障时TR2各采样点有功功率分布Fig.15 Distribution of active power at each sampling point ofTR2under fault in branch BO

图16 AD支路故障时TR2各采样点有功功率分布Fig.16 Distribution of active power at each sampling point ofTR2under fault in branch AD

将故障特征测试样本输入PNN模型中测试，得到预测结果如表8所示。

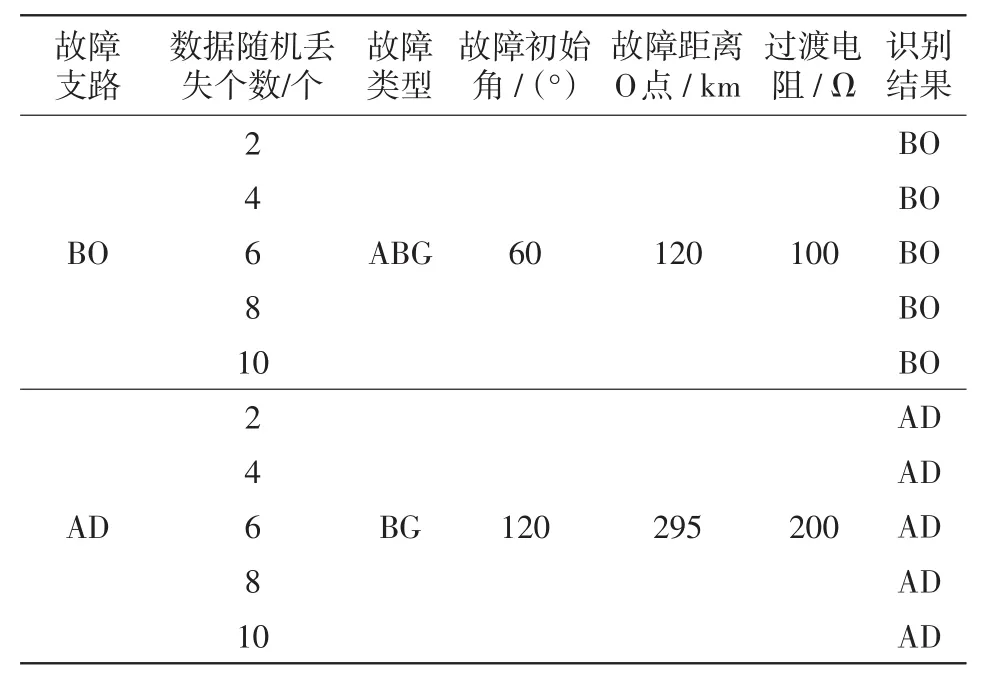
表8 区内支路BO和区外支路CF数据随机丢失下的测试集仿真结果Tab.8 Simulation and verification results of test set when data is randomly lost in internal branch BO and external branch CF

由表8可知，当T接线路区内外支路发生故障并发生行波波头附近采样点数据随机丢失时，该算法也能准确识别故障所在支路。

5.4.3 抗CT饱和能力分析

为验证本文所提保护算法的抗CT饱和性能，对T接线路各支路发生故障时CT饱和分别进行仿真分析，CT饱和仿真模型采用具有较好时频特性的非线性时域等效电路模型[23]。

以T接线路区内支路AO出现CT饱和为例，在T接线路区内支路AO出现CT饱和的条件下，在T接线路各支路仿真一组故障，得到6组T接线路故障特征向量，将故障特征测试样本输入PNN识别模型中测试，得到测试集预测结果如表9所示。

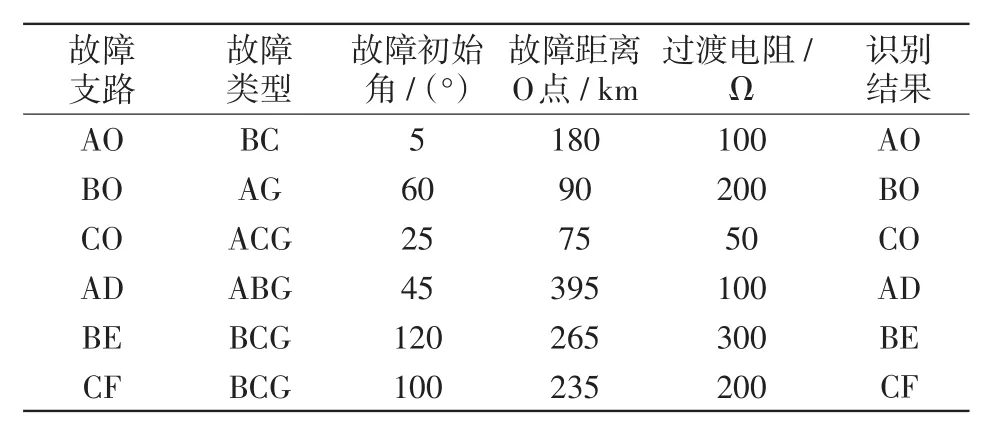
表9 T接线路区内支路AO出现CT饱和时测试集仿真结果Tab.9 Simulation results of test set when CT saturation occurs in internal branch AO of T-connection transmission line

由表9结果分析可知，当T接线路区内支路AO出现CT饱和时，该算法能100%识别故障支路，受CT饱和影响较小。

5.4.4 噪声影响分析

为验证信号在噪声影响下算法的可靠性，对T接线路各行波保护单元TRm测量得到的电压、电流信号中加入噪声，信噪比SNR（signal-noise ratio）为30～70 dB。

以行波保护单元测量到的电流行波在SNR为30 dB和S变换后频率为20 kHz为例。图17为T接线路区内支路CO故障行波保护单元测量的电流相关行波波形。

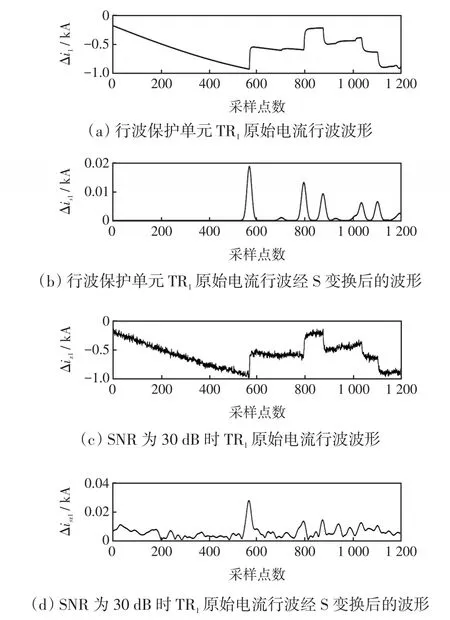
图17 T接线路区内支路CO故障行波保护单元TR1测量的电流相关波形Fig.17 Measured current-dependent waveforms of traveling wave protection unitTR1under fault in internal branch CO of T-connection transmission line

在区内AO支路和区外CF支路分别选取一种不同于训练样本的故障情况，在电压、电流信号中加入噪声，SNR分别为30 dB、40 dB、50 dB、60 dB、70 dB，仿真得到10组T接线路故障特征向量，将故障特征测试样本输入PNN识别模型中测试，得到预测结果如表10所示。

由表10可知，当区内支路AO和区外支路CF在不同信噪比故障下时，该算法能100%识别故障支路，受噪声影响很小。

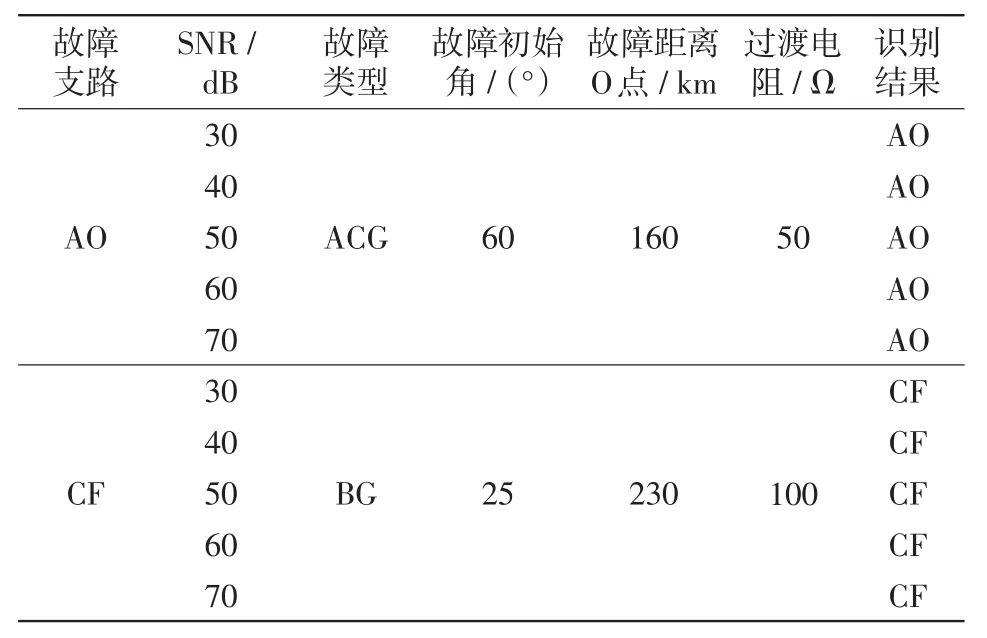
表10 T接线路区内支路AO和区外支路CF在不同SNR故障下的测试集仿真结果Tab.10 Simulation results of test set for internal branch AO and external branch CF in T-connection transmission line under different SNR faults

6 与传统算法的对比分析

6.1 算法动作速度分析

目前传统T接线路区内外故障识别算法广泛使用全周或半周傅氏算法进行计算，全周（半周）傅氏算法数据窗长为20 ms（10 ms），而本文算法所需数据窗长为0.1 ms，相较于传统算法，大大缩短了数据窗长，因此所提算法动作速度将远高于传统工频量T接线路区内外故障识别算法。

6.2 算法性能分析

目前，传统T接线路判据类故障识别算法大都未对算法在噪声影响、CT饱和及数据丢失情况下的性能进行分析，故无法验证算法在极端情况下能否准确判别故障。本文针对以上情况均对算法性能进行了仿真分析，仿真结果显示，本文所提算法在噪声影响、CT饱和及数据丢失情况下均能较好地识别故障。

6.3 识别精度分析

传统T接线路故障识别算法虽能识别T接线路的区内外故障，但是不能识别到区内外具体的故障支路，且部分算法识别效果易受其他变量影响。与传统T接线路故障识别算法[2-13]相比，本文所提算法不仅能准确识别区内外故障，而且能对具体的故障支路进行识别。

7 不同神经网络分类结果对比分析

为分析样本数据在不同神经网络中故障识别的精确度，分别将样本数据输入反向传播BP（back propagation）神经网络、极限学习机ELM（extreme learning machine）及PNN中进行测试，得到测试结果如表11所示。

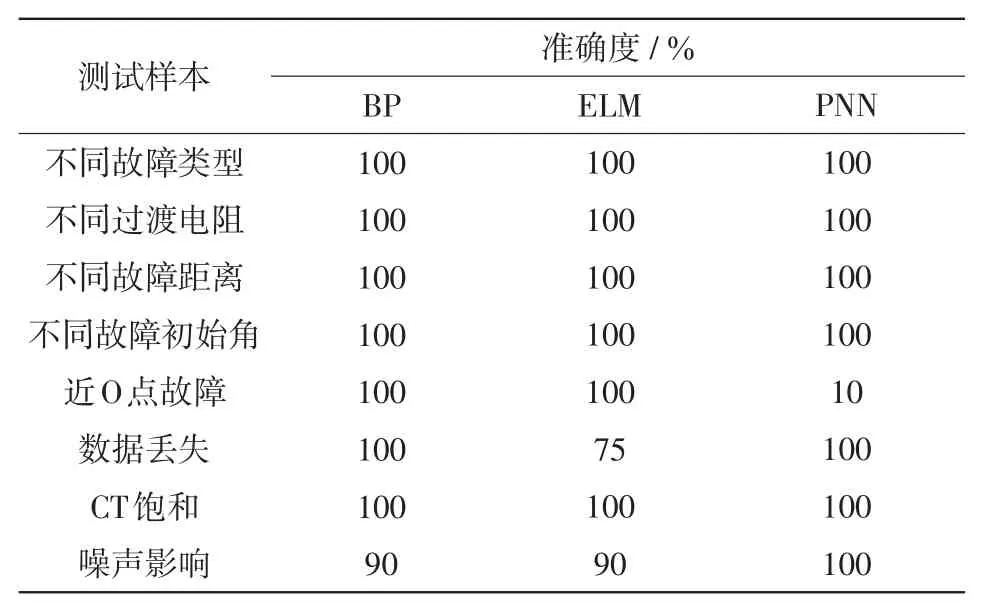
表11 不同神经网络分类结果准确度Tab.11 Accuracy of classification results of different neural networks

由表11结果分析可知，不同故障类型、不同过渡电阻、不同故障距离、不同故障初始角及近O点故障的测试样本在3种网络中均能准确识别故障；而在3类性能分析的测试样本中，仅PNN能准确识别故障。

8 不同电压等级及线路参数下算法可靠性分析

利用PSCAD/EMTDC电磁暂态仿真软件建立图1所示220 kV的T接线路仿真模型，T接线路各支路长度分别为AO=130 km，BO=100 km，CO=80 km，AD=50 km，BE=70 km，CF=60 km，其中输电线路参数如表12所示。

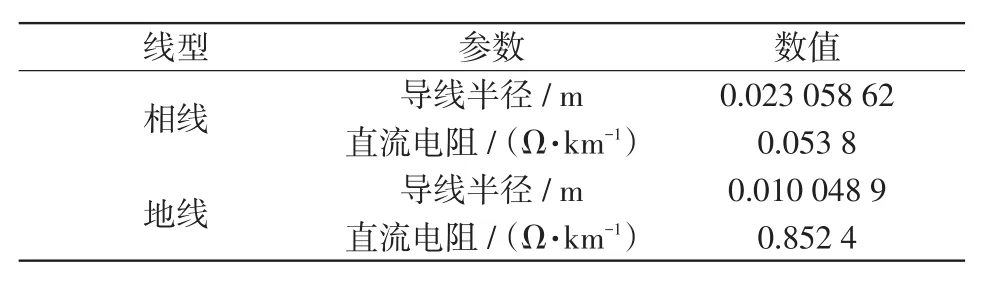
表12 仿真模型输电线路参数ITab.12 Transmission line parameters I of simulation model

训练样本由120组随机故障特征向量（由T接线路6条支路对4类故障情况随机各仿真5组故障）和30组近O点故障特征向量（区内3条支路各仿真10组近O点故障）组成。测试样本数据是在T接线路各支路下随机仿真4组故障，得到24组T接线路故障特征向量，将故障特征测试样本输入PNN识别模型中测试，得到预测结果如表13所示。由表13可知，本文所提算法在该电压等级及线路参数条件下均能可靠识别故障所在支路。