基于多数据融合的电机故障诊断方法研究

（河北机电职业技术学院电气工程系，河北 邢台 054000）

电机作为各类电驱设备的主要动力装置，具有结构简单、控制方便、能效高、无污染等优点，被广泛运用于各类机电设备。电机的运行状态不仅对其本身，更会对整个机电系统的正常运行产生巨大影响。然而，电机故障种类繁多，各种故障类型的征兆与表现又相似，且不同故障产生的原因也错综复杂，这给电机故障诊断带来了很大难度。若能在电机运行过程中精确地辨识电机运行状态及故障类型，便能极大地提高生产效率，降低维修成本。

传统的电机故障诊断方法多以单一的传感器数据信息为样本，对电机故障进行诊断。其中，定子电流信号是一种典型的故障判别依据，文献[1]提出一种对转子断条故障进行诊断的方法，对电机启动电流进行小波分析，实现了转子断条故障的在线诊断；文献[2]采用基于电机电流信号分析（motor current signature analysis，MCSA）的故障在线监测与诊断方法，通过分析定子电流的Hilbert模量频谱，实现了异步电机转子故障准确诊断；文献[3]提出一种电机典型故障通用诊断系统，通过理论推导确定了电流信号中的故障特征参数，并通过实验验证了所提出故障诊断系统的可行性。

电机振动信号也蕴含着一些典型故障信息，文献[4]提出一种基于小波变换和BP神经网络的电机故障诊断系统，通过小波变换从电机振动信号中提取到故障特征量，并通过BP神经网络进行故障识别，提高了故障诊断的准确性；文献[5]针对振动信号的特点，提出一种基于自回归（autoregressive，AR）模型的分析方法，消除了特征提取过程中的“频率模糊”现象，实现了对电机故障信息的快速提取；文献[6]通过分析气隙偏心故障与机座振动信号的关系，得到气隙偏心故障所对应的特征频率，并通过模拟试验对该故障特征频率进行验证；文献[7]以振动信号为依据，提出一种异步电机滑环面损伤的故障诊断方法，通过对比故障前后振动信号的小波能量谱分布及占比状况，得到故障特征信息，为电枢滑环面故障诊断提供依据。

此外，一些学者还通过分析电机转速信号以辨识电机故障类型，文献[8-9]提出一种阶次自分离方法，提取到蕴含在转速信号内部的异常波动成分及故障特征，实现了对轮毂电机的故障诊断；文献[10]针对定子电流中存在的电机断条故障特征频率易被基频淹没的缺陷，提出一种基于瞬时转速的电机故障诊断方法，研究发现，转速信号不仅能在频域上良好地反映故障情况，其波动程度和平均转速还能反映故障的严重程度。

分析上述研究可知，虽然电机电流、振动、转速信号中包含一些与电机某些故障类型相对应的可检测参数，然而，由于所建立的故障特征模型及电机运行环境存在很多不确定因素，单参数故障诊断具有不确定性，甚至可能会导致错误的诊断结果[11]。另外，电机实质上是一个机—电—磁强耦合的复杂系统，其故障特征与故障形式往往不是简单的一一对应，而是具有复杂的非线性关系。只有尽可能全面地收集故障特征，并对这些数据进行综合分析，才能对电机故障做出准确的判别。

针对上述问题，本文提出一种基于多传感器数据融合的电机故障诊断方法，振动加速度计和电流传感器被用于采集电机机座振动信号和定子电流信号，以此作为依据对电机故障进行综合诊断。简要介绍了多传感器数据融合技术的基本结构，分析了异步电机的故障机理，对基于神经网络学习算法和D-S证据推理的多传感器数据融合电机故障系统进行分析，并通过实例对系统的有效性进行验证。

1 多传感器数据融合技术

多传感器数据融合技术最初起源于军事应用场合，如通过综合分析多个雷达信号以达到精确锁定目标物准确位置的目的[12-13]。因多传感器数据融合技术具有较好的容错性、高精度、快速处理能力、强互补性等优势，逐渐在众多领域得到应用和发展。当多传感器数据融合技术应用于电机故障诊断过程时，可将其看成一种通过对多传感器获得的故障特征信息进行综合分析，以准确辨识电机故障类型的过程。根据融合对象或融合过程发生的阶段，可以将数据融合抽象为3种形式：数据层融合、特征层融合和决策层融合。这3种结构层次各具特色，具体分析如下。

图1为数据层融合结构图，该结构不对传感器采集到的信号数据做任何处理，而是直接融合传感器信号，根据融合结果的特点，提取相应特征，从而进行故障识别，这种结构对传感器的同质性要求较高，信息耗损率最小，但系统容错性较差，计算量也很大。

图1 数据层融合结构图Fig.1 Structural diagram of data level fusion

图2为特征层融合结构图，这种结构首先需要提取各传感器采集到信号的特征信息，并将这些特征信息进行融合，根据融合结果识别故障信息。这种结构对各传感器的同质性不作要求，系统的容错性较好，计算量也较小，但在特征提取过程中会存在信息丢失。

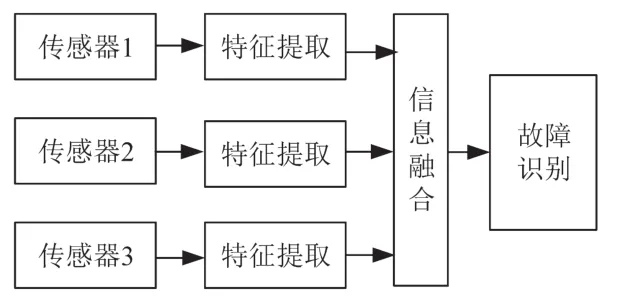
图2 特征层融合结构图Fig.2 Structural diagram of characteristic level fusion

图3为决策层融合结构图，决策层融合针对所有传感器信息进行单独处理，分别提取特征信息并进行识别，并对单独识别的结果进行融合，从而进行故障判别。该结构对原始信息的损失量最大，对前期特征提取和故障识别要求较高，但容错性较高，计算量也最小。本文正是基于这种融合模式，对所提出电机故障诊断系统进行设计。

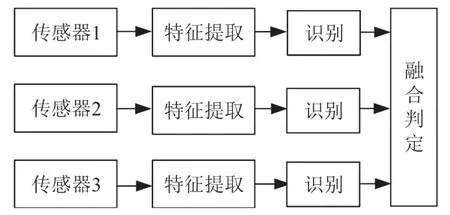
图3 决策层融合结构图Fig.3 Structural diagram of decision level fusion

2 电机故障机理

异步电机的主要故障类型包括电气类故障与机械类故障，其中，电气故障包括定子绕组故障、转子绕组故障等；机械故障包括转子故障、轴承故障等。要想实现对电机故障的精确辨识，首先需要对电机的故障机理进行分析。

2.1 基于定子电流的电机故障机理

当定子绕组发生短路故障时，定子绕组的对称性会遭到损坏，其电流成分中的奇次谐波，特别是5次谐波会因三相绕组的非对称性而增强[14]。定子短路故障体现在定子电流的特征频率为

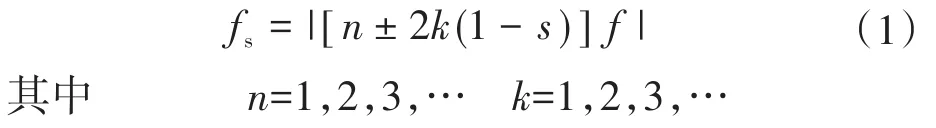
式中：f为电源频率；s为异步电机转差率。

当电机存在定子短路故障时，分析定子电流的频谱图，会发现定子短路故障状态时的定子电流频谱图中特征频率处幅值较正常状态时偏大，且偏离程度与故障严重程度成正比，这样就可以对定子短路故障进行识别。

当异步电机没有故障时，定子电流频谱中只有一个工频成分。而当存在转子断条故障时，在定子电流频谱中距离电源频率2s位置会存在一个边频带，基于定子电流的转子断条故障判别原则是电流频谱中存在如下式所示的特征频率：

2.2 基于振动信号的电机故障机理

当异步电机没有故障时，定子机座受旋转力作用，会发生频率为2f的振动。但当异步电机存在定子绕组故障时，机座振动信号会加强，且在正常频率之外，还会存在4f，6f，8f等谐波成分。通过振动加速度计检测电机机座的振动信号的特征频率，即可判别电机是否存在定子绕组故障。

当异步电机存在转子偏心故障时，机座振动信号中存在2种特征频率，分别为静态偏心特征频率fjt与动态偏心特征频率fdt，其频率值分别为

异步电机轴承故障诊断也多以振动信号为依据，当电机轴承存在故障时，机座振动信号的频谱中会含有相应特征频率成分，且不同故障类型所呈现出特征频率也不同，其中，轴承外圈故障频率fod、内圈故障频率fid、滚珠故障频率fbd、保持架故障频率fcd分别为

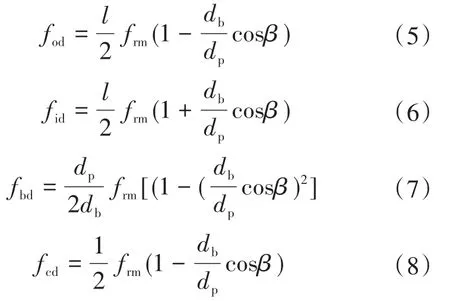
式中：frm为电机转动频率；db，dp分别为轴承滚动体直径与保持架直径；l为轴承滚动体个数；β为滚动体接触角。

3 基于神经网络和证据理论的电机故障诊断系统

3.1 BP神经网络学习算法

BP神经网络具备强大的非线性数据处理能力与学习能力，以及抗干扰性等优势，非常适合电机故障诊断等故障特征不确定性强的场合。电机是一种机电强耦合系统，建立准确的数学模型具有很大难度。针对这种问题，引入神经网络算法，可以将电机故障诊断等效成一个模式辨识的问题，即把电机的运行状态分为正常状态与故障状态，故障的种类各式各样，诊断其故障类型即为一种模式识别的过程。这为电机故障诊断提供了一种新途径。

BP神经网络学习算法的基本特点是数据向前传播，误差向后传播，如图4所示，包括输入层、隐含层和输出层。其中，wih为输入层到隐含层的权系数，who为隐含层到输出层的权系数，BP神经网络在使用前需输入一定样本（每个样本必须包含输入向量与期望输出值）进行网络训练，即输入数据的正向传播与偏差的反向调整，对不同层之间的权系数进行优化，直到误差量达到所需的最小误差阈值之内。训练结束后，便可以针对类似的输入样本，输出误差最小的结果。

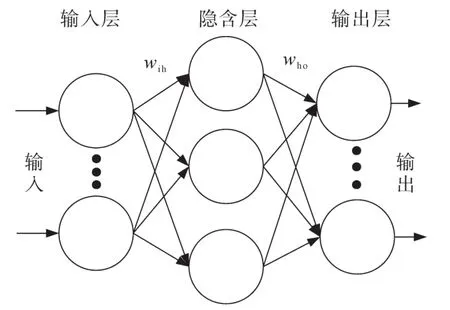
图4 BP神经网络结构示意图Fig.4 Structural sketch of BP neural network

3.2 D-S证据理论

D-S证据理论实质上是一种辨识框架，可用Θ表示，具体来说，Θ为一个完备的命题集合，其集合元素为一系列互斥命题，m为各命题的可信度函数，也可以称之为mass函数，对任意一个命题A，mass函数满足以下2式：

由式（9）可知，命题集Θ中不包含空命题。而式（10）反映了命题集Θ中所有命题所赋予的可信度之和（也称为总信度）等于1。

当已知所有命题的mass函数，则可以求出命题集Θ中某一具体命题A的信度函数Bel（A）和似然函数Pl（A），即

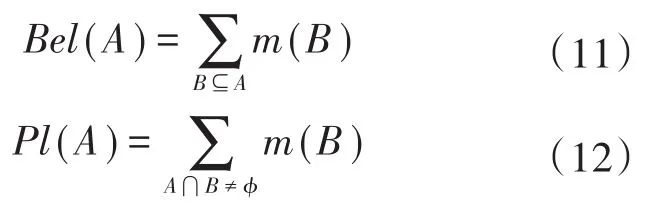
由式（11）、式（12）可知，命题A的信度函数是指所有属于A命题集合中所有命题元素的mass函数之和。似然函数是指所有与A相交不为空的命题集合中所有命题元素之和。命题A的信度函数和似然函数组成的闭合区间[Bel(A),Pl(A)]为命题A的信任区间，是对命题A的信任程度的一种较为抽象的描述，如图5所示。

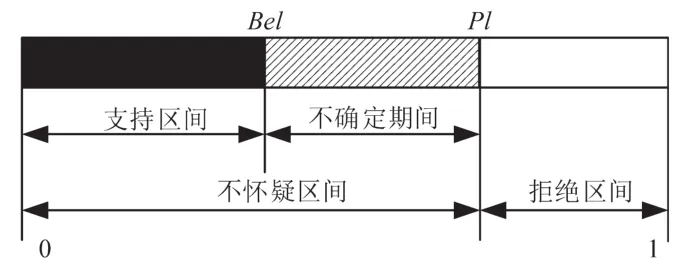
图5 命题不确定性示意图Fig.5 The schema of propositional uncertainty

当2个均指向命题A且相互独立的证据的mass函数分别为m1和m2，这2个证据所对应的命题元素分别为Ai和Bj时，基于D-S证据合成规则，可以将命题A的mass函数融合为

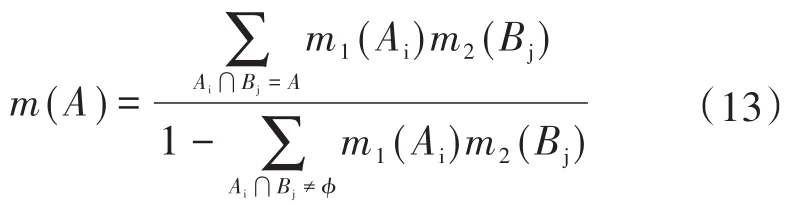
当具体到电机故障诊断过程中时，电机所有可能发生的故障集合构成辨识框架，而各种故障类型所可能表现出来的症状构成证据集，每种症状对应的各种可能性故障均存在一定概率，即为该症状下所对应的故障类型可信度函数。

3.3 基于神经网络的电机故障证据推理

在电机的故障诊断过程中，不同传感器多点测试所测得的参数众多，从各测点提取到的故障特征可能存在随机性和矛盾性。若将大量高维特征信息同时输入同一神经网络进行处理，会导致训练时间过长，诊断效果变差，甚至会导致网络输出结果发散。为避免这种情况，各测点信号首先由对应神经网络进行局部诊断，将所测得特征信息空间分解为多个证据空间，构造相应可信度函数，并利用证据融合规则将各证据体合成为一个新证据体，以确定新的信任区间。最后，利用证据理论将各证据空间进行决策融合，得出证据融合后的结果，实现对电机故障的准确判断，基于BP神经网络算法的多证据融合故障诊断流程以及系统原理图如图6和图7所示。

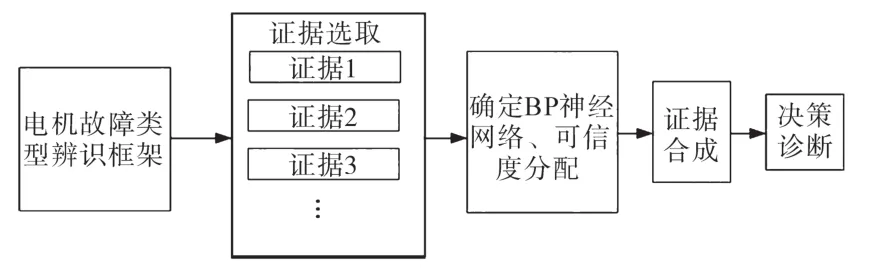
图6 多证据融合电机故障诊断流程Fig.6 Multi evidence fusion motor fault diagnosis process

图7 基于多传感器的电机故障诊断系统Fig.7 Motor fault diagnosis system based on multi-sensor

4 应用实例

以某型异步电机为例，对本文所提出基于神经网络和证据理论的多传感器数据融合电机故障诊断方法的有效性进行验证。图8为电机故障诊断试验测试原理图。

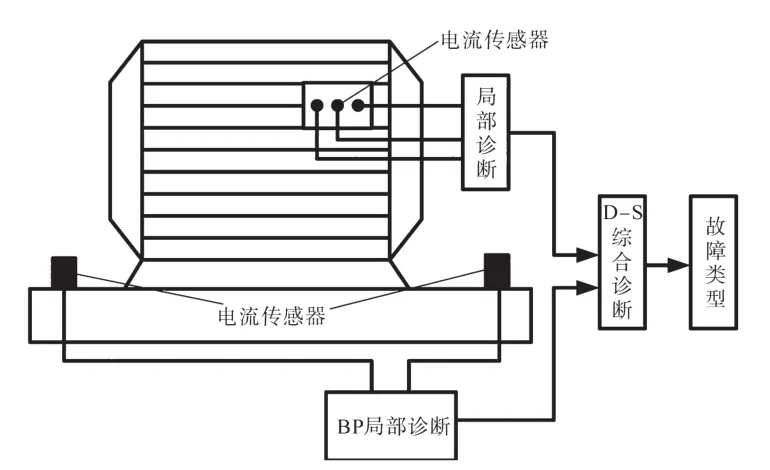
图8 电机故障诊断测试原理图Fig.8 Schematic diagram of motor fault diagnosis and test

首先，在试验台上模拟电机4种典型故障：定子绕组短路、转子断条、轴承故障、转子与轴承复合故障。在测试过程中，采用振动加速度计和电流传感器，分别测得电机在无故障工况及4种故障工况下的机座振动信号和定子电流信号，利用小波变换得到所测信号在各频段的小波能量谱，并对能反映电机故障的子频段能量ai进行提取，得到电机故障的特征向量为[a1，a2，a3，…]。

在提取到电机故障特征向量后，需要对BP神经网络进行训练，此例中用到2个传感器，因此需要对2个BP子网络进行训练，每个子网络的输入单元个数等于故障特征向量的维数，这里取特征向量为6，即在振动信号和电流信号的小波变换结果中选取6个子频段能量。2个子网络所用到的训练样本参数如表1和表2所示。

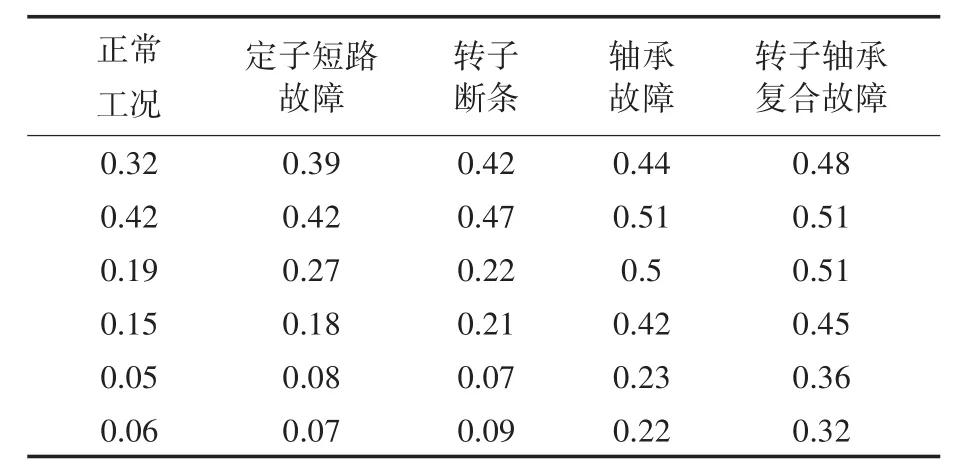
表1 振动特征向量训练样本Tab.1 Training samples of vibration eigenvector

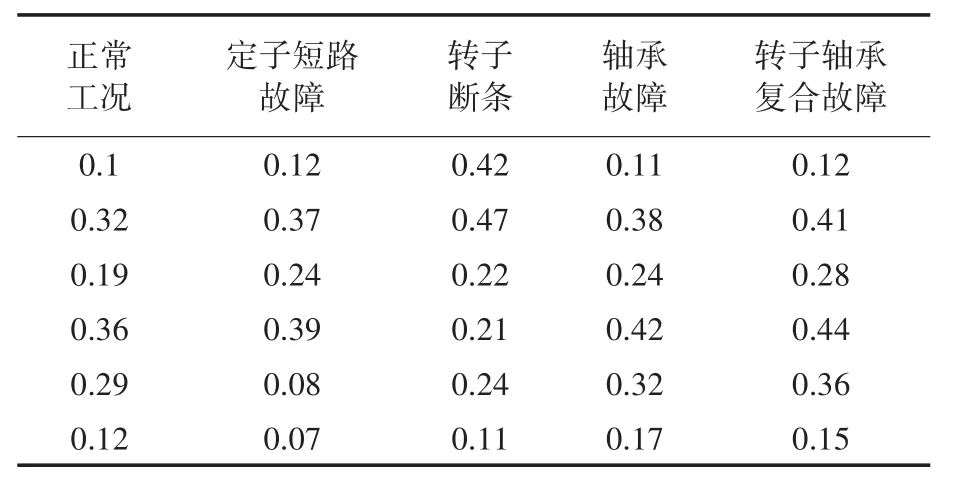
表2 定子电流特征向量训练样本Tab.2 Training samples of stator current eigenvector

2个BP子网络的的输出节点个数均为5个，代表着上述的电机运行状态，表3为2个BP子网络的期望训练结果。

表3 BP神经网络期望输出Tab.3 Expected output of BP neural network

为降低测试成本，选择了异步电机轴承滚珠故障进行实验，对振动加速度计和电流传感器信号分别进行小波变换处理后，得到轴承滚珠故障所对应的振动特征向量与电流特征向量，利用这2组特征向量对BP神经网络进行学习训练，得到了2个BP子网络的初步诊断结果为

O振动=[0.0035,0.120 5,0.040 0,1.0060,-0.0870]

O电流=[-0.0832,0.0985,0.1440,1.2035,-0.0088]

为提高故障诊断的准确性与可信度，基于DS证据理论对上述2个输出结果进行融合。具体来说，证据理论辨识框架中的元素为Ai（i=1～5，分别对应着正常工况、定子绕组短路、转子断条、轴承故障、转子轴承复合故障）。

结合电机轴承故障工况下的BP子网络输出结果，得到相应可信度函数，如表4和表5所示。需要注意的是，表中的m（φ）对应着诊断结果为不确定的可信度函数。

表4 振动信号子网络可信度函数分配Tab.4 Distribution of reliability function for vibration signal subnetwork

表5 电流信号子网络可信度函数分配Tab.5 Distribution of credibility function for current signal subnetwork

基于D-S证据融合规则，得到融合诊断结果如表6所示。综合分析图4～图6可知，当证据融合判定准则为Bel＞0.5且m（φ）＜0.2时，若只以电流子网络的置信区间作为诊断依据，则诊断结果只能为不确定，而经过数据融合之后，电机轴承故障工况所对应的置信区间与不确定结果的可信度函数较单一信号子网络时小，提高了轴承故障这一诊断结果的可信度，也符合实验中的故障模拟工况。

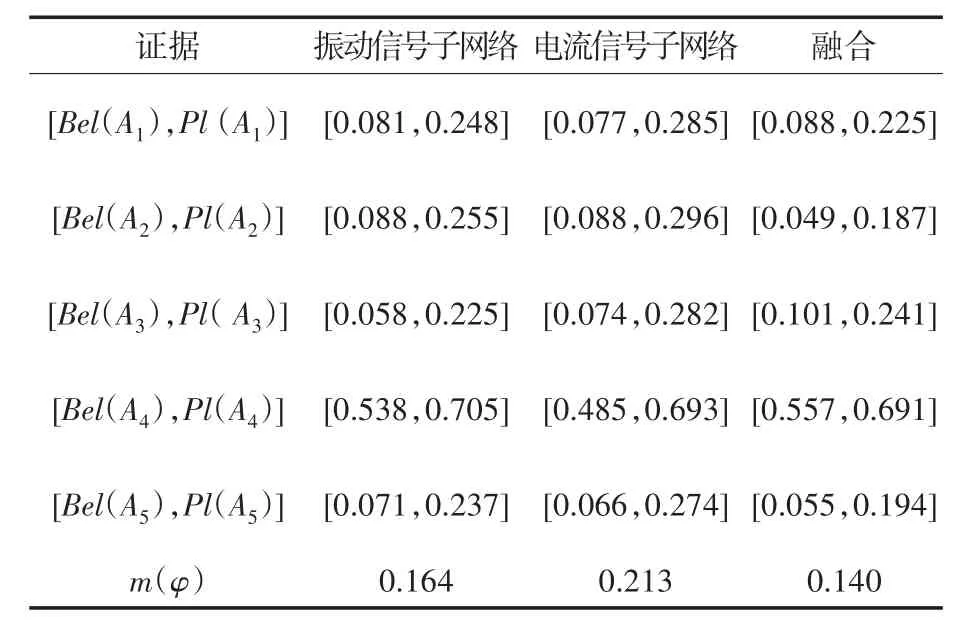
表6 电机各运行状态的置信区间Tab.6 Confidence intervals of motor operation states

5 结论

为克服基于单传感器的电机故障诊断方法存在的不确定性大、精度较差等缺陷，提出一种基于BP神经网络和D-S证据理论的多传感器数据融合电机故障诊断方法，振动加速度计和电流传感器被用于采集电机机座振动信号和定子电流信号，以此作为依据对电机故障进行综合诊断，并结合神经网络学习算法和D-S证据推理理论，对电机的故障类型进行综合诊断。通过对电机轴承故障诊断实例进行分析，验证了所提出系统的有效性，研究结果表明：采用基于多传感器数据融合的故障诊断系统可以高置信度地诊断出电机的故障类型。