光储气微网优化运行研究

马磊，张超，钟鸣，李剑，刘晓华，袁博

（1.国网新疆电力有限公司，新疆 乌鲁木齐 830063；2.中国电力科学院有限公司，北京 100192）

随着化石能源的枯竭及环境问题日益凸显，可再生能源与清洁能源的发展受到了广泛关注，其在能源结构中的占比逐年增加。由于光伏发电和风力发电具有不确定性及间歇性的特点，目前还存在着较大的弃风弃光量。此外，我国天然气资源较为丰富，天然气发电仍是拉动天然气消费的重要推手[1]。我国天然气发电行业处于刚起步阶段，具有较为广阔的发展前景。如何提高可再生能源的利用率、减小可再生能源发电并网对电力系统产生的影响以及对天然气发电参与电网调峰的研究是现如今的热点问题。

在我国推动能源互联网建设下，天然气以其清洁、高效和可储存性，在与可再生能源融合发展中具有明显优势。目前国内外学者对于互补发电系统的研究有如下几个方面：文献[2-4]对于含电转气（P2G）设备的电-气互联系统的控制策略、容量规划进行研究，建立了多目标优化运行模型，但是多目标优化问题由于各目标权重的确定未能有统一标准，因此最优解并不唯一；文献[5-7]以系统运行成本最小为目标，开展了基于风光气储多能互补的联供系统优化经济调度及容量配置的研究，发挥能源各自的优势，提高了能源利用效率的目的，但系统所体现的效益评价指标也较为单一，未考虑到碳排放成本对效益的影响；文献[8]考虑可靠供能率，提出长期优化电-气互联能源系统规划模型；文献[9]建立水火电力系统发电模型，充分利用了水资源的存储特性，起到了较好的调峰效果，但容量较小，在负荷波动的工况下，承担基荷的火电机组出力曲线变化较大，并且在火力发电的约束中未设置火电机组的备用容量，存在一定的运行风险；文献[10-11]构建了风电与火电机组协同调度模型，协调效果好，但是受火电机组的调峰能力制约，风电机组容量在模型中所占的比例不高；文献[12]分析了多能源系统运行对电网运行可靠性的影响，建立了包含多个能量载体的能量系统通用建模和优化框架；文献[13]建立了风水气互补发电模型，克服了水能容量小，风电出力波动的缺陷，但部分气电机组在负荷低谷时运行效率较低，在一定程度上增加了一次能源的消耗。

在研究中将燃气发电机组碳排放税纳入微网运行优化中，依据微网系统实际运行条件和运行方式，以此为基础建立一种以经济运行为目标，包含光伏发电、储能系统及天然气发电系统的协同优化运行模型。之后，针对粒子群算法存在的早熟缺陷，提出一种狼群与粒子群混合算法，将狼群算法中的搜索策略应用在前期对约束条件及最优结果的求解过程中。所提出的混合算法能够弥补传统粒子群算法的缺陷，解决其早熟及易陷入局部最优的问题。通过算例验证，混合算法的求解结果降低了光储气微网运行的经济成本，减小了微网系统在高峰时段对电网的负担。

1 光储气互补微网结构及模型

1.1 光储气微网系统结构

光储气互补发电系统结构如图1所示，微网由光伏发电系统、天然气发电机组、储能系统及负荷所构成。其中，光伏发电系统在白天8：00—18：00时刻出力，并且光伏发电系统存在着间歇性与波动性，因此需要天然气发电机组及储能装置对其输出的功率进行平抑，减小出力波动对配电网的影响。天然气机组提供大部分的电能。同时，储能装置根据当前微网的运行状态及时充放电，对微网内功率波动起到缓冲作用。

图1 微网系统结构图Fig.1 Structure of the micro-grid

当微网系统内负荷处于低谷时，若光伏发电量较为充足，则调整部分天然气机组减小或停止出力，同时对荷电量较低的蓄电池组进行充电；当负荷处于较高时段，且光伏出力较低时，调整燃气机组增加出力，同时利用蓄电池的富余电量，微网系统中多余的电能根据实时电价并入电网。

1.2 光伏发电系统模型

光伏发电系统的输出功率[14]如下：

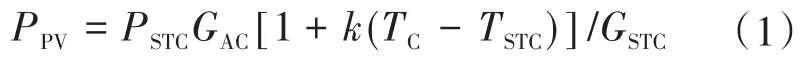
式中：PSTC为光伏发电系统在标准测试条件下的最大功率值；GAC，GSTC分别为当前日照辐射强度与测试条件下的日照辐射强度；TC，TSTC分别为工作点光伏电池板温度与测试条件下的参考温度。

光伏发电系统的日常运行无须考虑燃料成本及碳排放。

1.3 微燃机组

天然气发电所用燃气轮机作为动力装置，其优点有燃料选择范围广、燃料利用率高、启动快、废气几乎无污染且余热可回收等。在发电过程中，压缩的空气进入燃料室与天然气混合燃烧，通过涡轮透平装置，产生机械能，进而带动发电机完成发电过程。

燃气轮机工作耗气量[15]公式如下：

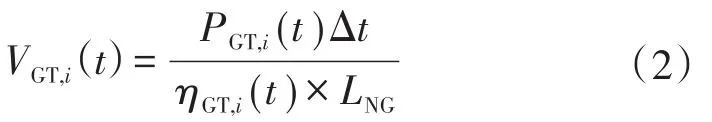
式中：PGT，i（t）为第i台燃气发电机在第t时刻的发电功率；ηGT，i（t）为第i台燃气发电机在第t时刻的发电效率；LNG为天然气低热值，取9.7（kW·h）/m3。

燃气轮机的发电效率公式用三阶多项式来描述：

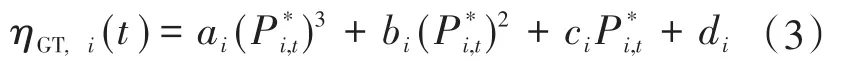
式中：ai，bi，ci，di为效率系数，通过曲线拟合得出；P*i，t为燃气发电机在t时段内电功率的标幺值。

1.4 储能装置

储能装置是光储气微网中关键部分，能够平抑光伏发电波动，缓解微网中供需不平衡的矛盾。同时，储能装置在电价低谷时大量充入，在用电高峰期电价较高的时段，将存储的电能供给负荷或电网中，减小了微网的运行成本，起到削峰填谷的作用。t时刻储能装置充放电公式[16]如下：

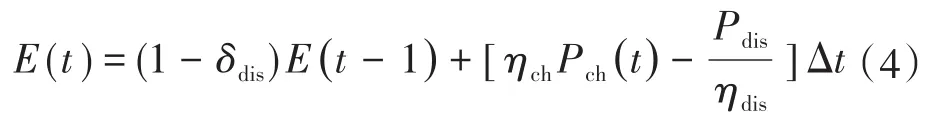
式中：E（t）为储能电池在t时刻的剩余容量；δdis为储能电池的自放电系数；ηch，ηdis分别为储能装置的充、放电效率。

2 光储气微网运行模型及求解

微网中的储能装置、光伏发电系统、天然气发电机组的协同配合是保证微网稳定运行的前提。以微网的经济运行成本及碳排放税成本之和最小为目标，综合考虑各项约束条件、分时电价等因素，建立微网调度运行模型。调度模型的决策变量为各天然气发电机组的出力、光伏发电系统出力和储能系统的充放电功率及荷电量状态。综合上述条件，并依据前述光储气微网结构及实际运行状态搭建优化运行模型。

2.1 目标函数

微网优化运行的目标函数以日运行成本最小和碳排放量最少为目标。若以多目标问题考虑，对最优调度进行求解时，各目标权重系数的确定具有较强的主观性，不能客观衡量其求解结果。为此，碳排放最小化目标转换为碳排放税成本最小，具体为日运行下的碳排放量与税率的乘积。由此，最小日运行成本及最少碳排放量两个目标则可以转变为日运行成本与碳排放税成本之和最小，上述问题变为了对单一经济性问题的求解。

微网的日运行成本中包含天然气发电成本和微网向电网购售电的交互成本。以24 h为调度周期，对各小时内的天然气发电成本、电网交互费用及碳排放税成本求和，得到光储充微网在调度周期内的总费用。目标函数如下：

式中：F为微网在调度周期T内总运行费用；CNG（t），CGR（t），CCO2（t）分别为t时刻的天然气发电成本、微网与电网交互费用和微网碳排放产生的相应税收；SCH4为单位体积天然气价格；VGT，t为 t时刻内发电的耗气量；Sgb（t）为t时刻电网电价；Sgs（t）为t时刻上网电价；Pmg（t）为当前时刻微网与电网的交互功率；αGT，i为天然气发电机组CO2的排放系数；βmg为电网供电对应排放系数[17]。

其中，天然气发电成本CNG包括购气费用SCH4VGT，t以及燃气机组启停费用Ssc，交互费用CGR为微网的购电费用与向电网售电收益之差，碳排放税收CEN为各天然气机组出力及电网交互功率对应产生的碳排放量与税率单价λCO2的乘积。

上述以微网碳排放税来衡量微网碳排放量，以运行成本及碳排税成本之和最小作为优化目标求解调度问题，对微网的运行评价能够更客观。之后考虑微网系统实际运行过程及方式，制定协同运行模型的约束条件，使微网各系统满足实际运行工况。

2.2 约束条件

2.2.1 功率平衡约束

微网在t时刻各系统发电出力值等于微网内负荷与电网交互电功率之和，如下式：

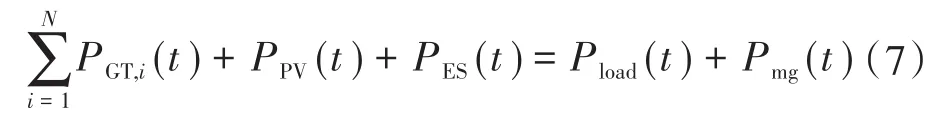
式中：PGT，i（t），PPV（t），PES（t）分别为第i台天然气发电机组在t时刻的发电功率、光伏发电系统在t时刻出力值、储能系统在t时刻的充/放电功率；Pload（t），Pmg（t）分别为t时刻微网用电负荷、t时刻微网与电网交互功率。

2.2.2 光伏发电功率约束

光伏发电某时刻的出力值为各光伏电池组功率之和，光伏电池的功率上下限约束为

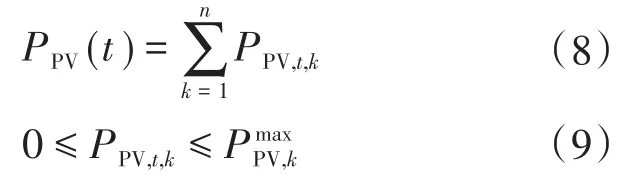
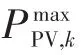
2.2.3 天然气发电机组约束

机组的变化功率和启停次数需要设置在一定范围内以满足机组的爬坡功率限制以及降低机组的启停成本。天然气发电机组的约束有功率上下限约束、机组爬坡功率约束和机组启停次数约束，公式如下：

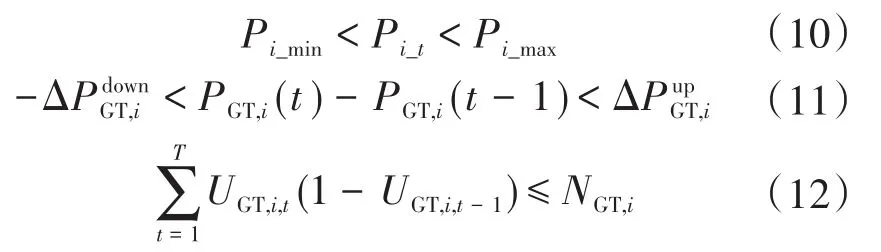
式中：ΔPGT，i为连续时间段Δt内机组功率变化范围；UGT，i，t表示第 i个机组在时间 t时刻的启停状态，0表示停机，1表示启动。

微网内部的优化调度需考虑日前负荷预测值及光伏出力预测值，由于预测值存在一定的预测误差，因此需要留有一定的备用旋转容量，以降低微网内部供需不平衡的风险，以及降低微网波动对配电网造成的电压和频率偏差影响。因此天然气发电机组的功率如下：

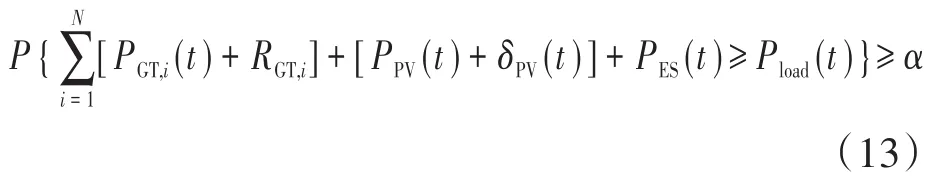
式中：RGT，i为微网中第i台可控机组在时段所提供的备用值；置信水平α为备用约束不等式成立下所满足的概率值；δPV为对应于光伏预测值的误差正态分布均值。

2.2.4 储能系统约束

蓄电池作为储能装置中的主要设备，起到了对电能的缓冲作用。当电价较低或微网发电功率高于负荷需求时，驱动储能装置蓄能；电价较高或微网发电功率不能满足负荷需求时，蓄电池释放存储的电量，缓解电量供需矛盾。考虑到实际运行情况，在整个调度周期内，设置蓄电池初始容量等于调度结束容量约束如下式，以便微网在下一调度周期内稳定运行。

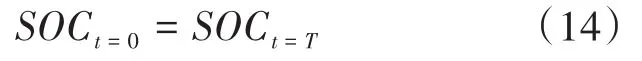
储能电池的充放电功率约束和容量约束公式如下：

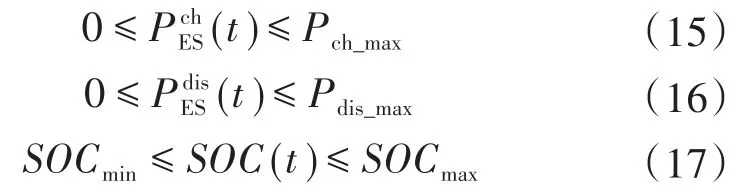
2.3 求解算法

传统的粒子群算法中惯性权重ω随着迭代次数的增加而递减，但是由于粒子的启发性得不到提高，常常会使得种群陷入局部最优解[18-19]。粒子群算法速度及位置更新公式如下：

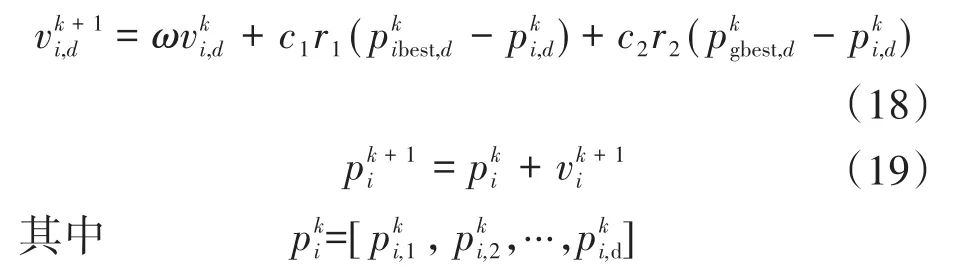
权重系数ω仅与迭代次数有关，没有与计算中实际过程状态建立联系，因此缺乏一定的合理性。在此考虑到传统粒子群算法的缺陷，提出将狼群算法中的搜索策略结合粒子群算法应用于对模型约束度的求解中。

狼群算法为近年来通过仿生自然界中的狼群捕食行为而提出的群体智能算法，该算法抽象出狼群捕食过程中存在的游走、召唤及围攻行为以及优胜劣汰的狼群更新机制。

传统粒子群算法收敛速度较快，但在求解前期存在全局搜寻能力较弱及易陷入局部最优的缺点。狼群算法具有较强的全局搜索能力，但寻优过程较复杂，且收敛速度不如粒子群算法，同时不同粒子间缺乏信息的交互，使得探狼粒子游走相对单一、盲目化。为充分发挥上述算法各自的优势，以及弥补两种算法各自的缺陷，提出狼群-粒子群混合算法（WPA-PSO），并利用该混合算法对前文搭建的模型进行求解。

狼群算法前期探狼的游走搜索阶段，通过探狼对不同方向的嗅寻，能够感知猎物浓度的变化。探狼分别向h个方向分别前进一步，并记录h个方向上猎物气味浓度的大小，并退回原位置。之后，探狼向气味最浓的方向前进并进行下一步的嗅寻。在狼群算法中探狼的游走行为如下：

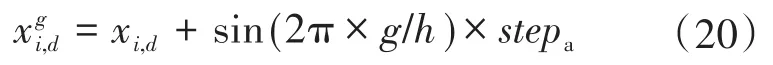
由于狼群算法在求解前期，探狼粒子具有从当前位置向各方向的试探性搜寻行为，因此相较于粒子群算法，对最优解的搜索更为全面，全局寻优能力更高，在前期不易陷入局部最优。在搜寻过程中，考虑到传统狼群算法在前期搜索中不同狼之间没有信息交互行为，不能及时把握全局状态，游走行为较单一，因此结合粒子群的速度更新思想，引入了信息交互行为。以个体狼粒子适应度值作为猎物气味浓度，适应度的值越优，则猎物气味越浓。所提出的混合算法中的探狼搜寻更新公式如下：

在混合算法后期精细求解的过程中，速度公式与粒子群算法的速度更新公式类似。但考虑到作为头狼的最优位置可能不是理想解，因此对狼群速度更新方向做出修改，前进方向选择为最优头狼和次优头狼的折衷方向。混合算法中粒子前进的步长公式及狼群更新公式如下：

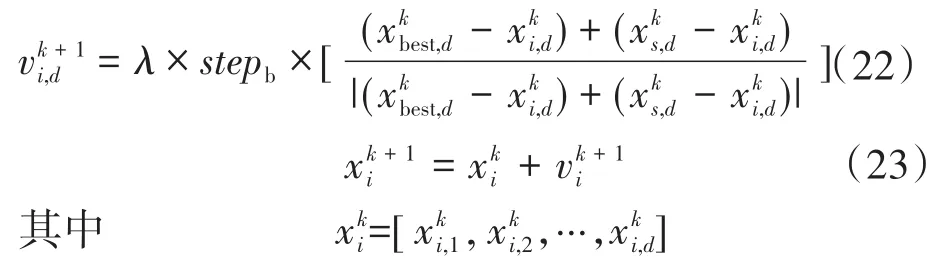
当最优狼粒子经过t次迭代后，若其适应度值未作改变，此时引入狼群算法内的优胜劣汰制，淘汰掉适应度较低的若干粒子，保持种群的多样性。优胜劣汰机制为：若在连续t次内最优粒子产生了更新，此时无需更改；若在连续的t次迭代后，最优粒子的位置未得到更新，则此时淘汰一定数量适应度较差的粒子，保持种群的多样性。综上，混合算法的具体流程如下：

1）在解空间中初始化狼群粒子的空间位置坐标，根据初代适应度值选择最优粒子作为头狼。

2）探狼向h个方向搜寻，并同时向适应度更优探狼粒子靠近，当第gb方向上的猎物气味更浓时，更新探狼xi位置，若在此次嗅寻未发现更优位置，则继续搜寻行为直到最大搜寻次数Ts。

3）在混合算法精细搜索阶段，调整粒子以步长λ·stepb向头狼最优粒子及次优狼粒子靠近。

4）当聚集过程中出现距离猎物更近，位置更优的粒子时，该粒子替代成为头狼或次优狼。

5）在粒子聚集过程中，记录迭代次数，若在t次迭代后头狼位置未得到更新，则淘汰一定比例的适应度较差的粒子，同时在解空间中随机生成新粒子实现狼群更新。

6）继续迭代更新，若满足目标适应度值，停止迭代输出结果。若达到最大迭代次数，则转向步骤2），开始新一轮游走行为。

3 算例及分析

3.1 算例描述

算例求解以国内某地区微网案例为背景，选择冬季和夏季典型日的负荷预测曲线及光伏出力预测曲线如图2，光伏发电系统始终工作在最大功率点处，算例以24 h为周期，时间间隔为1 h。

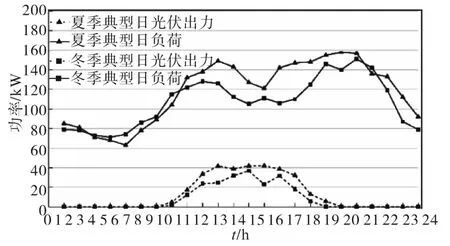
图2 夏冬季典型日光伏出力预测及负荷预测曲线图Fig.2 Typical daily PV power generation and load forecasting curves in summer and winter

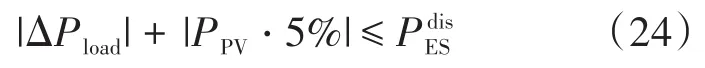
图2中微网负荷波动最大约为23 kW，最大预测误差约为5 kW，由此储能电池充放电功率应在30 kW较为合适。

同时，按国家标准GB/T 33589—2017《微电网接入电力系统技术规定》第4.1条的规定，微电网独立运行模式下向负荷持续供电时间不低于2 h。考虑到机组故障问题，假设最坏情况为：在晚间负荷高峰时段，某台燃气机组发生故障，且光伏由于没有太阳辐射不出力。由此储能电池容量应满足：

微网内能量的主要来源为太阳能、天然气和电能，实验中忽略太阳能的发电成本。算例中天然气低热值 LNG取 9.7（kW·h）/m3，天然气单价为[21]2.5元/m3。分时电价如表1所示。

表1 分时购、售电价格Tab.1 Electricity prices in the different periods

微网优化调度运行以运行成本及碳税之和最小化为目标，运行成本包括微网燃料消耗成本、电网交互成本及碳排放成本。目标函数为

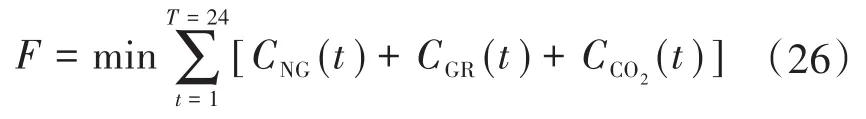
其中，天然气发电机组燃料消耗成本CNG、电网交互成本CGR及碳排放成本CCO2由式（6）计算得到。光伏发电系统作为微网发电设备，存在波动性和不可控性，因此在调度运行的求解中将其看做值为负的负荷，将微网内用电负荷预测值与光伏发电功率预测值的差值作为微网系统的等效负荷。

以碳排税来衡量微网运行过程中CO2的排放量，天然气发电机组二氧化碳排放系数αGT取值为0.619 kg/（kW·h），电网以燃煤电厂作为电力来源计算，碳排放系数βgrid取值为0.971 kg/（kW·h）。

由于地方税率有所区别，算例中的税率取为7$/t。通过将最少碳排放问题和最低运行成本两个目标转换为碳排放税与运行成本之和最小，进而将多目标优化问题转变成对单一经济性问题的求解，以降低求解难度。

根据上述各设备参数，天然气发电出力约束有4个方面：发电机爬坡功率限制、出力约束、停启次数限制及备用容量限制，分别如下：

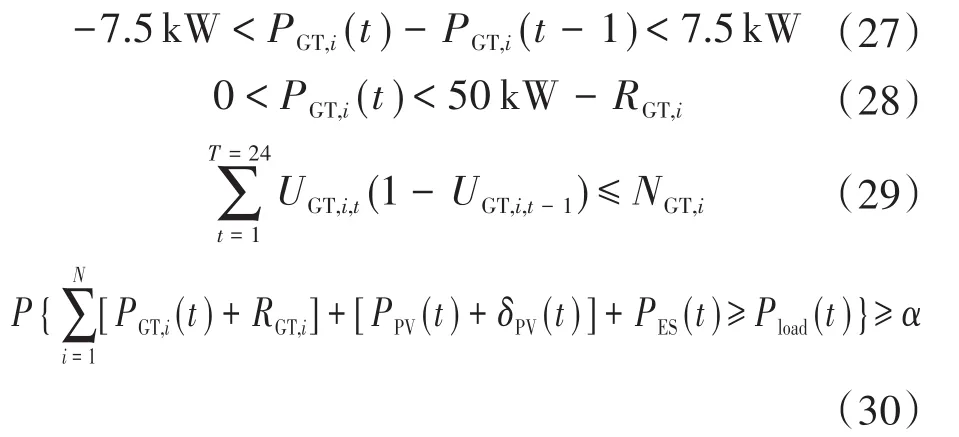
由于当燃气轮机低于一定功率运行时，会出现燃烧不稳定以及燃烧室的差压波动，在此限制其最低出力为10 kW。对于停启次数的限制，实验中设置的启停次数NGT，i为6次。由于光伏发电功率预测中存在一定的预测误差，因此需要根据式（30）留有一定备用容量，文中预测值的波动方差取值为0.01，置信水平α取90%。储能系统约束公式为

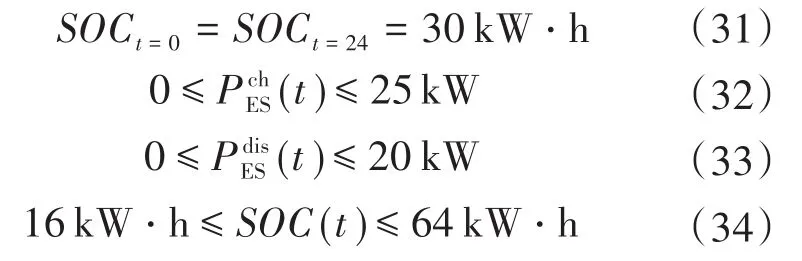
微网内各时刻功率等式约束为

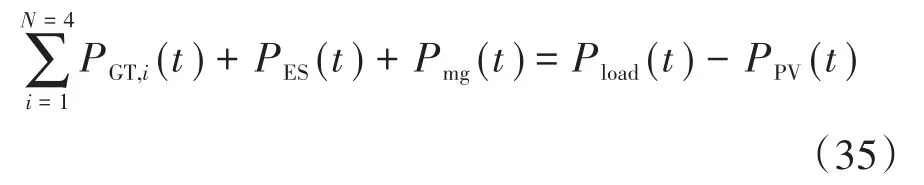
每个时刻微网内的4台天然气发电机组功率PGT，i、光伏发电功率 PPV、电网交互功率 Pmg以及蓄电池充放电功率PES应满足当前微网电负荷Pload。

由上述公式，设置求解算法的决策变量维度为 X=[PGT1（1） PGT2（1） PGT3（1）PGT4（1）PES（1）Pmg（1）PGT1（2）PGT2（2）PGT3（3）…Pmg（24）]，共6×24维。

3.2 求解结果及分析

算例选取自适应权重粒子群算法（APSO）和自适应步长狼群算法（AS-WPA）作为对比算法。

以约束度适应值为目标，求解得到狼群-粒子群混合算法（WPA-PSO），APSO与AS-WPA的对于违反约束的适应度变化曲线，适应度值越小，则违反运行约束的程度越轻，当适应度为0时，即为满足运行约束。其结果如图3所示。

图3 约束值适应度曲线Fig.3 Constraint value fitness curves

从算法迭代过程中可以看出，所提出的混合算法，在前期相较于其他两种算法，具有更快的收敛速度。其中，WPA-PSO混合算法平均在60次迭代之内满足运行约束要求，AS-WPA和APSO的平均求解迭代次数分别为84次与93次。由此表明，WPA-PSO混合算法能够更快地使粒子满足于运行约束。

算例对于约束条件的求解共进行了200次实验。WPA-PSO混合算法求解成功率为94%，高于AS-WPA的88%成功率和APSO的79.5%成功率。改善了粒子群算法早熟的缺陷，基本解决了其易陷入局部最优问题。寻优精度具有明显提高。

三种算法对于夏季和冬季典型日下的日运行成本结果如表2所示。

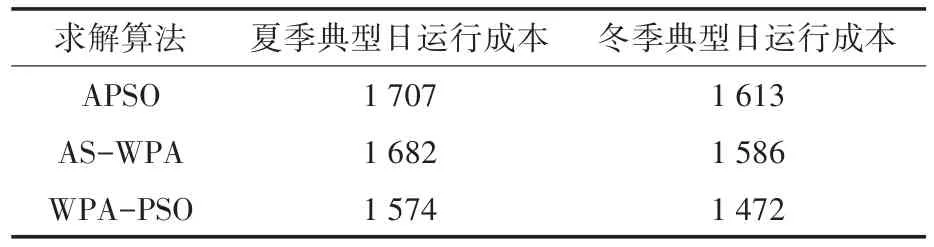
表2 典型日下三种算法运行成本结果Tab.2 Microgrid operating costs under three algorithms

AS-WPA算法和APSO算法对于光储气微网的调度优化结果分别如图4和图5。

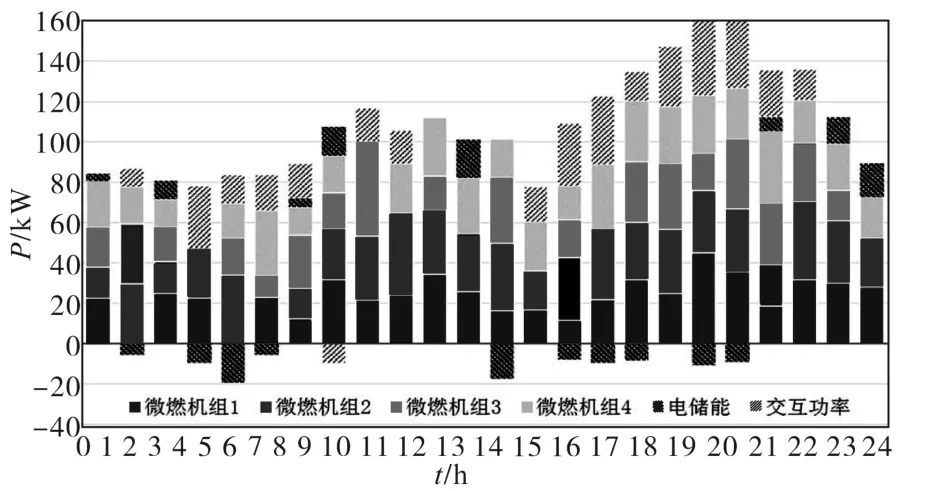
图4 夏季典型日AS-WPA求解结果Fig.4 Adaptive step wolf pack algorithm results

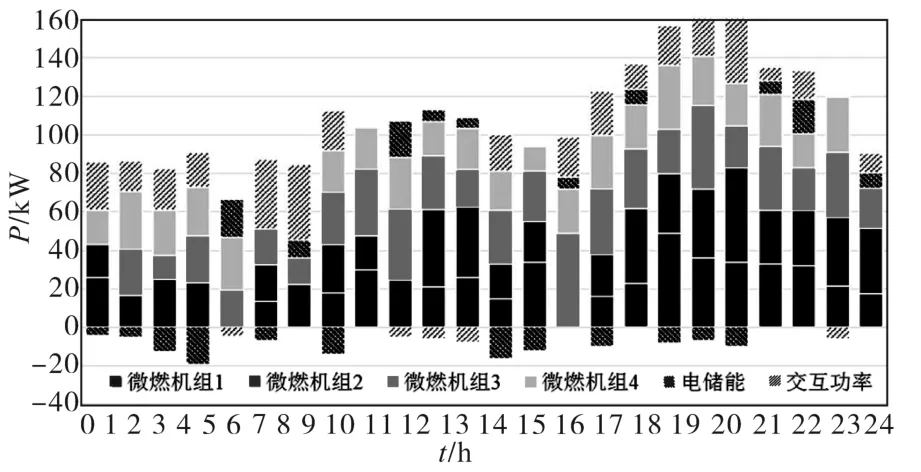
图5 夏季典型日APSO求解结果Fig.5 Adaptive weight particle swarm optimization algorithm results

从自适应步长狼群算法（AS-WPA）和自适应权重粒子群算法（APSO）优化调度结果中可以看出，在低谷时刻的机组大部分都在启动状态，以较低效率运行，未充分利用燃料，造成了燃料的浪费；部分机组启动较为频繁，造成调度周期内停启成本较高；同时，储能电池充放电较为混乱，在负荷及电价尖峰时段，由于储能电池的荷电量较低造成储能装置未启动，没有分摊微网内的负荷，因此对电网造成了一定的负担。WPA-PSO算法优化调度结果如图6所示。

从WPA-PSO算法的优化结果中可以看出，该算法在应用于微网调度时微燃机组启停次数更少，降低了机组启停成本；在负荷低谷23：00—7：00及平段14：00—15：00时刻，WPA-PSO混合算法求得的机组出力值为仅由部分机组启动，其余停止，使得微燃机组工作在高效率点处，对天然气的利用率较高，并在电价及负荷低谷时刻对储能系统进行充电。当负荷高峰10：00—12：00，18：00—20：00及电价高峰时刻，控制储能装置向电网及微网系统释放电能，一方面缓解电网压力，另一方面减小了微网日常的运行成本，对电网起到了一定的削峰填谷作用。

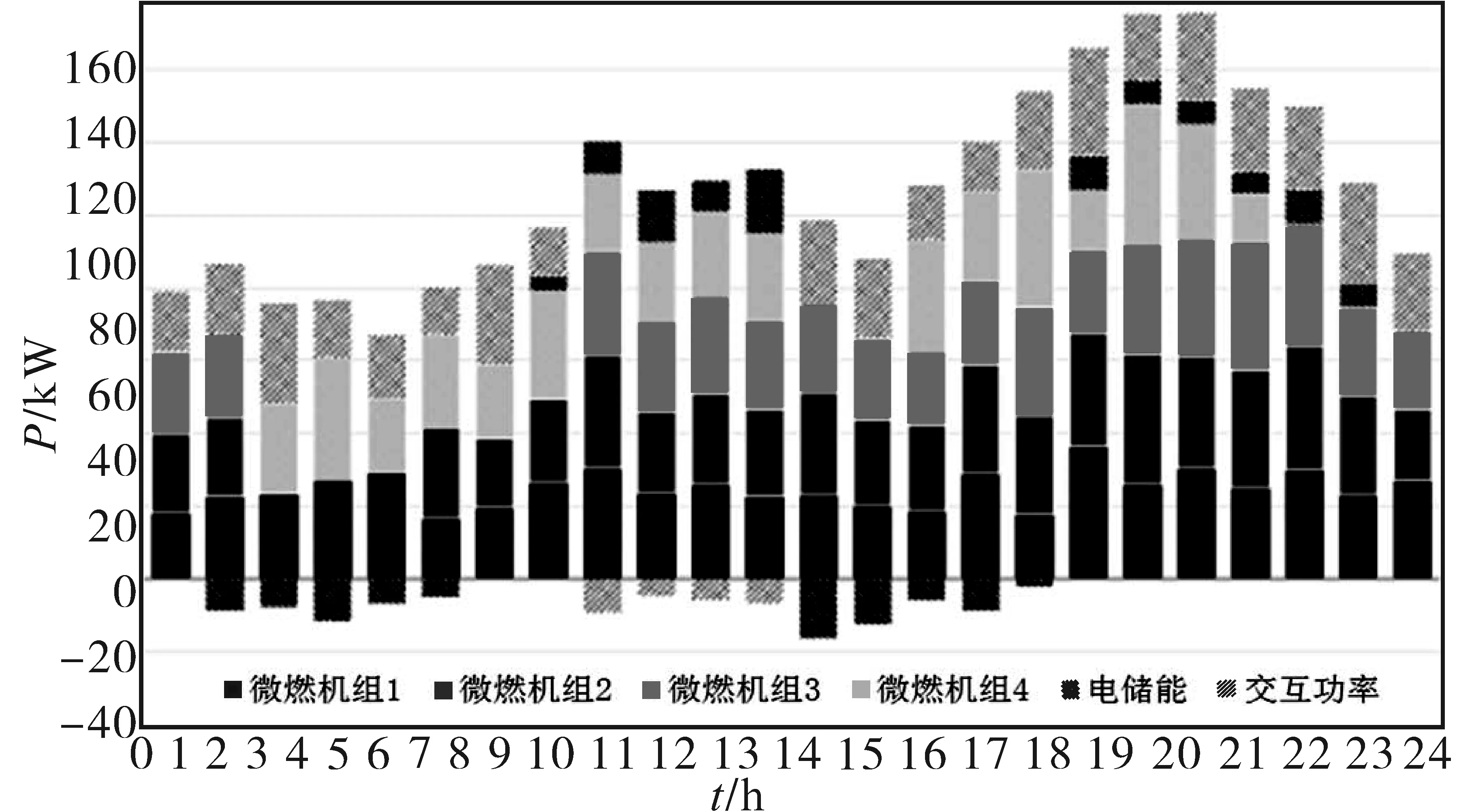
图6 夏季典型日WPA-PSO求解结果Fig.6 WPA-PSO hybrid algorithm results

4 结论

文章依据微网系统实际运行工况和运行方式，以微网经济运行成本与碳排放治理成本之和最小为目标，建立了光储气微网协同优化运行模型。在分析传统粒子群算法的缺陷及狼群算法搜索策略的优势基础上，提出结合狼群搜索及淘汰机制的狼群-粒子群混合算法，并对研究中所搭建的模型进行计算验证。算例结果表明，相较于另两种对比算法，所提混合算法具有收敛速度更快、寻优精度更高的优点，使微网运行成本降低了6.4%，具有较好的应用前景。

研究所提出的混合求解算法对于微网系统模型的求解能够充分发挥微型天然气机组和储能系统的快速响应特性，减小了微网内可再生能源及负荷波动对配电网的影响，充分发挥微网内设备参与电网削峰填谷的作用。该模型及求解算法可以为光储气型微网的规划及经济运行提供一定的参考。此外，文中对于光伏发电预测精度误差的研究及天然气发电中热能的利用可作为下一阶段的研究方向。