基于SIMD的Square Root函数高性能实现与优化*

赵永浩,贾海鹏,张云泉,张思佳

(1.大连海洋大学信息工程学院，辽宁 大连 116023;2.中国科学院计算技术研究所计算机体系结构国家重点实验室，北京100190)

1 引言

平方根函数是基本的数学运算，也是处理器软件生态的重要组成部分。平方根函数的应用极其广泛[1]，可应用于图形处理器[2]、神经网络、计算机图形学和积分计算等科学领域。随着处理器架构的不断发展和完善，为了更好地支持和完善计算机的并行性,SIMD(Single Instruction Multiple Data)技术得到了快速的发展，已经被广泛使用到各种处理器上，并成为其中重要的技术,比如ARM架构的NEON指令集[3]，MIPS的MSA指令集和Intel x86架构中的MMX/SSE/AVX指令集[4]。NEON技术是对ARM Cortex-A和Cortex-R系列处理器中SIMD的扩展。NEON寄存器存储的是同一数据类型的向量，相比其他指令其优点是NEON指令可以对4个32 bit和2个64 bit的元素同时进行计算，并且还支持int、float、double等多种数据类型。该技术通过同时计算多个元素，加快计算速度，来达到提升整体性能的目的。

研究基于SIMD的平方根函数的高性能实现与优化具有十分重要的研究价值和实际意义。针对ARM架构处理器在市场供不应求的现状，SIMD向量化技术也在不断发展，所以完善ARM SIMD生态是十分重要的工作。目前基于SIMD NEON技术的高性能函数实现与优化的研究比较少，可以查阅到的资料有对处理器的扩展函数库的实现与优化，另一个是针对SIMD功能的函数优化算法，但这2项研究的时间较早，技术还不算完善。所以，利用SIMD NEON技术针对ARM架构进行平方根函数高性能实现具有重大意义。平方根函数高性能实现与优化[5]的基本思想是，在保证精度的条件下，尽可能地提升算法的性能。所以，设计高精度、高性能的平方根函数算法是本文的研究重点。就目前来说，处理器已经提供了sqrt指令，可实现平方根的SIMD求解，但其性能较低。在测试数据长度相同的情况下，直接调用SIMD求平方根的指令，计算时间需要0.214 570 ms，而本文的计算方法只需要0.069 750 ms，性能可以提高将近3倍。平方根函数计算方法是基于数值分析[6]领域的方法，其中用到的算法是平方根倒数和泰勒展开[7]，使用2个算法的目的是使计算在满足计算精度的同时尽量提升计算时间性能。本文实验中，将与本文算法与libm算法库[8]进行性能比较，并和处理器本身提供的sqrt指令进行比较。本文的主要贡献如下所示：

(1)依据计算平方根函数的方法，得出平方根函数高性能实现的思想和原理；

(2)总结出平方根函数高性能实现和优化的具体方法；

(3)实现了具有高性能平方根函数的算法，并与libm算法库进行了性能对比。

2 相关工作

本文主要基于数值分析的相关原理利用SIMD对平方根函数的高性能实现进行优化；现有的一些函数库提供了计算平方根函数的算法，如ARM_M算法库、ARM Performance Library(ARMPL)和libm算法库。本文最后要与libm算法库和处理器提供的sqrt指令在计算性能和精度2个方面进行对比。

2.1 libm

Newlib是一个面向嵌入式系统的C运行库，对于与GNU兼容的嵌入式C运行库，Newlib并不是唯一的选择，但Newlib具有独特的体系结构，使得它能够非常好地满足嵌入式系统的要求，此外，Newlib具有很强的可移植性和可重入性，且功能完备，已广泛应用于各种嵌入式系统中。

libm算法库是C运行库Newlib的一部分，也是Newlib中一个完整的IEEE数学库，提供了用于嵌入式系统接收float和double 2种类型参数的函数。

在基于 SPARC 的系统上，libm 中的初等函数是使用表驱动算法和多项式有理数近似算法的组合实现的，可以实现更高的性能或精确度。

在基于x86的系统上，libm的某些初等函数是使用x86指令集中提供的初等函数内核指令实现的；其他函数是用基于 SPARC 的系统上的相同表驱动算法或多项式/有理数近似算法实现的。

libm 中常见单精度初等函数的表驱动算法和多项式/有理数近似算法都将准确的计算结果传送到最后位置单元内，通过运算法则直接分析这些误差界限。

2.2 ARMPL

ARMPL是ARM公司为满足科学计算和高性能计算社区应用开发需求所推出的，针对ARM V8-A系列处理器精准化的商业数学函数库。ARMPL通过充分利用芯片合作伙伴为ARM V8-A架构系统单芯片设计的创新特性和功能，确保基于ARM V8-A架构的高性能服务器和系统到达极致，在科学计算应用程序使用中，可以确保获得的结果更加准确。

2.3 ARM V8 架构

ARM 是一种负载性的存储体系结构，是RISC 处理器的典型之一。ARM V8兼容了ARM V7，是一个支持64 位指令集的ARM 处理器架构，引入64 位体系结构之后，还保持了与现有32 位系统结构的兼容性。

ARM V8 提供了31个64 bit 通用寄存器和32 个128 bit 浮点寄存器，浮点寄存器在执行指令时一条指令可以操作多个操作数，可以提高指令的执行效率。ARM V8架构提供了sqrt指令，可以直接对浮点数进行开平方计算。本文将与sqrt指令在性能方面进行对比。

2.4 向量化SIMD

SIMD用一个控制器来操作多个处理单元，时间上的并行性是通过对数据中的每个元素进行相同的计算来实现的。目前该技术已经在多个平台使用，而且每个平台都拥有不同的指令集。编译器把代码翻译成SIMD指令的操作叫做SIMD并行化或者SIMD向量化。在执行SIMD指令时，通过一条指令可以同时对多个元素进行计算。例如，在一个128 bit的向量寄存器下，每次编译时，可以对4个float类型数据或2个double类型数据进行计算。理论上，在性能方面，SIMD 指令是普通运算的4倍。

2.5 平方根算法综述

目前计算平方根的方法有以下几种：Newton-Raphson(牛顿一拉斐森)算法[9]、Goldschmitdt算法、SRT-Redundant算法[10]和Non-Redundant算法[11]。

Newton-Raphson算法[9]已经广泛应用于许多工程。该算法的实质是利用泰勒展开定理把非线性方程展开为线性方程，在迭代过程中需要使用乘法操作来计算除数的倒数，这会导致延时变大，此外，迭代的周期数与初始值有关，所以没有固定的周期。

Goldschmitdt算法是Newton-Raphson迭代算法的改进，通过增加子操作之间的并行性来减小延时。

上述2种算法的缺点是运算速度慢，在精度上无法满足IEEE浮点数标准规定的精度要求。

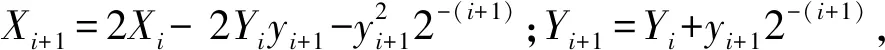
Non-Redundant算法[11]与SRT-Redundant算法类似，但该算法是用补码的形式来表示平方根，其运算精度低。

3 研究背景

本文平方根函数主要使用的是平方根倒数算法和泰勒展开[12]。

3.1 平方根倒数速算法

IEEE 754标准浮点数在内存中的存储方式如图1所示。

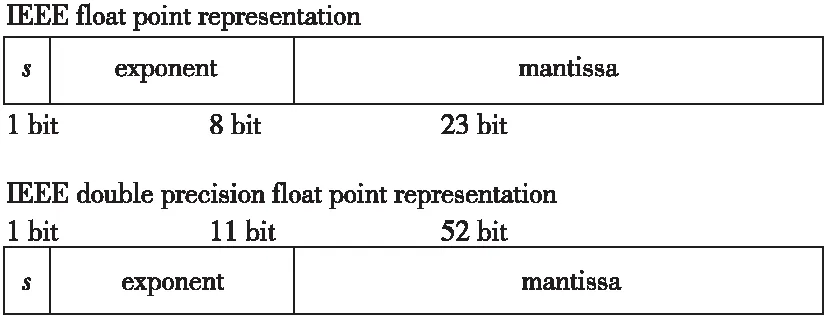
Figure 1 IEEE 754 float point format图1 IEEE 754浮点数格式

IEEE 754标准中,一个规格化浮点数的真值可以表示为式(1)所示：

x=(-1)s*(1.M)*2e

(1)

其中,s代表符号位，e(exponent)代表指数，单精度浮点数e=E-127，双精度浮点数e=E-1023,1.M代表尾数域，

平方根倒数速算法(Fast Inverse Square Root)[13]是适用于快速计算积的算术平方根的倒数的一种算法，公式如式(2)所示：

(2)

其中，x是符合IEEE 754标准格式的32位浮点数(该算法是为IEEE 754标准中的浮点数存储规则设计的)。该算法的优势在于减少了求平方根倒数时浮点运算操作带来的巨大运算消耗，大大提高了运算速度，比调用sqrt指令快了约20倍。但是，该算法所得到的结果精度不够，所以本文将采用泰勒展开公式对其精度进行补偿。

3.2 泰勒级数

如果函数f(x)在点x0处可以求导，则有:

f(x)=f(x0)+f′(x0)(x-x0)+o(x-x0)

(3)

当|x-x0|的结果很小时，则有：

f(x)≈f(x0)+f′(x0)(x-x0)

(4)

等式右边是等式左边的近似值，但右边的式子明显精度不高，与等式左边相比误差过大。所以，可将上式推广至高次多项式：

f(x)=f(x0)+f′(x0)(x-x0)+

(5)

等式右边的多项式次数越高，对应结果的精度也越高。但是，若要达到可以满足条件的精度，有时相应的多项式次数会过高，造成计算时间增加到无法接受的地步。

(6)

4 平方根函数的算法实现

本文研究了4种类型的平方根函数的计算方法，包括单精度浮点数、双精度浮点数、单精度复数和双精度复数，每一种类型函数的实现都是基于C语言的代码进行SIMD并行优化[15]。下面主要介绍计算每种数据类型平方根函数的算法的高性能实现的原理及其计算方法。

4.1 单精度浮点数的算法实现

就目前来说，处理器已经提供了计算sqrt的指令实现平方根的SIMD求解，但是在性能方面比较差。在测试数据长度相同的情况下，直接调用SIMD求平方根的指令，计算时间需要0.214 570 ms，而本文方法只需要0.069 750 ms，性能可以提高将近3倍。

(7)

(8)

(9)

将(x/x0)-0.5根据泰勒公式展开,得：

(10)

最终表达式为：

(11)

在计算过程中，用平方根倒数的算法得出的结果只能精确到前8 bit，所以本文用泰勒展开对精度进行补偿,来确保计算精度。具体计算过程如算法1所示：

算法1单精度浮点数的计算

Input:x0。//约等于x的数

Output:y。

1．a←rsqrt(x)；

2．b←x*a；

3．y5←0.5*a；

4．y9←0.5 *(1-ab)；

5．y11←b*(1+0.5*(1-ab))；

6．y5←0.5*a(1+0.5*(1-ab))；

7．y←y11+(x-y112)*y5。

通过该计算过程计算得出的结果，在性能和精度方面相比直接调用sqrt指令有了很大的提升，性能方面可以提高大约7倍；精度方面，平方根倒数算法可以精确到前8 bit，此后用泰勒展开的方法对精度进行补偿，2种方法结合在一起，既保证了性能，也达到了对精度的要求。

4.2 双精度浮点数的算法实现

(12)

具体包括如下步骤：

步骤2对尾数域1.M进行计算，如果直接对1.M开根号计算，不仅计算的时间较长，而且计算结果会有很大误差。所以，本文将1.M拆分成2个单独的部分分别进行计算。令1.M=x，然后将x表示为x0和x1，对x0进行计算用的是开根号取倒数的方法，此方法只针对单精度浮点数；对x1进行计算用的根据泰勒展开公式的方法。具体算法将在后面介绍。

(13)

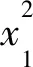
(14)

最终的计算公式为：

(15)

需要使用联合体(union)来把输入重新解释为浮点数、整型数和无符号整型数，并且通过联合体可以使用逻辑运算求得浮点数的指数位和尾数位。

使用union将双精度浮点数x重新解释为一个无符号的整数，通过逻辑运算取出指数位，以判断浮点数x指数的奇偶性。下面介绍对指数位的计算过程：

(1)首先，为了将11位的指数位取出，利用union将64位浮点数重新解释为64位无符号的整数。

(2)用0x7ff000000000000与重新解释为64位无符号的整数进行“与”运算，通过运算可以得到指数位e，其他位置0。

(3)接下来判断指数的奇偶性，将取出后的指数位按位取反,将～e和0x0010000000000000进行一次“与”运算。

(4)将(3)的计算结果加上0xbfd0000000000000,然后用该结果再减去(2)取得的指数位。

通过以上运算，得出e的表达式为：

(1)当e% 2=0时：

(16)

(2)当e% 2=1时：

(17)

接下来介绍对x0进行的运算。计算x0是按照单精度浮点数计算方式，在计算指数部分时，先对取出来的指数位进行奇偶性判断，然后再与x0整合在一起，形成一个新的单精度浮点数。计算x0的具体过程如下所示：

(1)设e是浮点数的指数位，将e与0x07f0000000000000相加,得到相加结果后再整体往右移动29位。

(2)用0x001fffffffffffff和重新解释为64位无符号的整数进行“与”运算，得到尾数位，其他位置0。然后将尾数位整体往右移动29位，这样双精度浮点数的尾数位上前29位为0，后23位为移动前尾数位的高23位，将其当作新浮点数的尾数位。

(3)将(1)和(2)的结果进行“或”运算后，组成一个新的32位单精度浮点数，然后就可以用平方根倒数的算法对其进行计算。

(4)平方根倒数算法得出的结果为float类型，需要将其转换成double类型，可使用SIMD NEON提供的verinterpretq_f64_u64转换指令完成。这条指令在转换后没有改变值，只改变数据类型。具体计算过程如算法2所示。

算法2x0计算过程

Input:x。

Output:y0。

1.DECLAREsrcAS DOUBLE_U；

2.DECLAREsAS FLOAT_U；

3.DECLAREtempAS FLOAT；

4.DECLAREe,src.uUNSIGNED INT；

5.src.f←x；

6.e←src.u&x_index；

7.e←0x001000000000000 & (～e)；

8.e←e+0x07f0000000000000；

9.e←e>> 29；

10.u←src.u&x_mantissa；

11.u←u>> 29；

12.s.u←u|e；

13.temp←rsqrt(s.f)；

14.y0←temp。

在计算x1时使用的是泰勒公式展开的方法，具体计算过程如下所示:

(1)在取出双精度浮点数的尾数位的运算中，使用0x001fffffffffffff和64位无符号整数进行“与”运算,得到的结果会保留指数位中最后一位。在下面的计算中采用位移的方法将指数位中末位的1去掉。

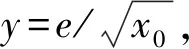
x1=1-x*y2

(18)

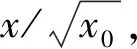
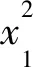
(19)

具体计算过程如算法3所示。

算法3x1计算过程

Input:x,y0。

Output:dst。

1.DECLAREb,dAS DOUBLE；

2.DECLAREe,u,EUNSIGNED INT；

3.DECLAREsrc,sAS DOUBLE _U；

4.src.f←x；

5.e←src.u&x_index；

6.e←0x001000000000000 & (～e)；

7.E←e+0xbfd0000000000000；

8.u←E-e；

9.s.u←u>> 1；

10.y←s.f*y0；

11.b←y*y；

12.x1←1-b*x；

13.d←x1*(x1*((x1*A5)+A4)+A3)+A2；

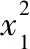
以上就是计算双精度浮点数的方法和过程，在保证双精度浮点数所能表示的数据精度和计算速度的同时，完成浮点数的开平方运算。

4.3 复数的平方根算法实现

在对复数进行平方根计算的时候，本文使用的是将复数的实部和虚部分开计算的方法。

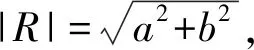
(20)

(21)

通过2个公式可以分别求出开根号之后的实部和虚部结果。具体计算过程如算法4所示。

算法4复数平方根的计算

Input：z=a+bi。

Output：w=c+di。

1．a=p_src.re；

2．b=p_src.im；

3．R=sqrt(a2+b2)；

4．c=sqrt((a+R)*0.5)；

5．temp.d=b*0.5；

6．d=temp.d/c。

5 SIMD优化

根据第4节函数算法的实现，在执行平方根函数的计算时，可以利用ARM NEON INTRINSIC指令对SIMD代码进行优化，以此加快对平方根函数的计算。此外，由于ARM NEON INTRINSIC提供的SIMD乘加指令的速度很快，因此可以在对程序进行精度补偿时使用泰勒展开公式，从而使用多个SIMD乘加指令加速运算。

在华为的鲲鹏920平台下，每个向量寄存器的长度为128 bit，所以可以同时计算4个float类型数据或者2个double类型数据。在ARM NEON INTRINSIC提供的指令中，只有load和store是寄存器与存储器之间的操作，其它指令都是介于寄存器与寄存器之间的操作。所以，可以把所有的计算放到寄存器中完成。

此外，在计算单精度浮点数时直接用了SIMD NEON的rsqrt指令，指令的功能是计算输入x的平方根再取倒数的值。此外，在计算双精度浮点数的过程中，采用了循环展开的方法，因为一个double类型数据是64 bit，而一个寄存器的长度为128 bit，所以用循环展开的方式，一次可以计算4个双精度浮点数，然后通过使用2个store把4个结果分别放到2个存储器中，这样可以加快计算速度。

6 性能评估

6.1 测试环境

(1)硬件环境。

本文实验采用鲲鹏920作为测试平台，鲲鹏920使用的是ARM架构，主频为2.6 GHz，测试环境的配置如表1所示。

Table 1 Hardware environment of experiment

(2)软件环境。

本文软件环境使用ARM V8架构提供的sqrt指令和C语言标准算法库作为计算速度的对比对象。对于单精度浮点数和双精度浮点数的测试样例输入，输出的平均精度需小于1E-6,最大误差小于1E-15才可以通过样例测试。

6.2 性能分析

如表2 所示，Open-v 是本文提出的算法实现，libm是C 语言标准算法库，sqrt 是ARM V8架构提供的求平方根函数的指令。表2中性能指标测试的输入向量长度为216。性能指标的单位是ns/item，即每个输入值计算所需要的平均时间。

Table 2 Performance comparison

由表2可以看到,本文工作相对于libm算法库在性能方面具有很大的提升，比libm算法库快了约7倍，比调用sqrt指令快了约4倍。并且可以看出算法对单精度函数的优化效果相较于双精度函数更明显。原因是计算float类型数据时可以直接调用指令来计算，缩短了计算时间。而在计算double类型数据时，算法比较复杂，首先，需要将尾数中的前23位取出来，当作float类型数据来计算；然后，再将计算结果转换成double类型数据；最后，需要利用泰勒展开公式对其展开多次，以达到对计算结果的精度要求。这是在算法上造成的性能差异的主要原因。另外的原因是在内存中的表示形式，float类型数据占4 B(32 bit)内存空间，double类型数据占8 B(64 bit)内存空间。在一个时钟周期内，CPU发射一个计算指令可以计算2个float类型数据，而double类型数据只能计算1个。综上所述，计算double类型数据要比计算float类型数据在性能上差距更大。

在性能指标测试的输入向量长度为65 536时，直接调用ARM V8架构提供的求平方根函数的sqrt指令计算时间为3 383 ns，而直接调用rsqrt指令计算时间为185 ns，可以看出速度比sqrt快约20倍，但是调用rsqrt指令计算，精度只能保证前8 bit，所以，本文使用泰勒展开公式对精度进行补偿。最后，本文算法既保证了计算速度，又保证了精度。

本文在基于ARM架构的鲲鹏920处理器上测试误差结果,2个对比对象是本文算法和ARM V8架构提供的求平方根函数的sqrt指令，结果如表3所示。

Table 3 Calculation accuracy

通过表3的测试误差对比情况可以看出，其单精度浮点数计算结果的平均误差为0.11E-08，而最大误差为1.15E-07。双精度浮点数计算结果的最大误差为0.20E-15，且双精度浮点数和双精度复数的平均误差为0.00E+00，最大误差不超过4.40E-16。

7 结束语

本文介绍并总结了基于SIMD的平方根函数高性能实现和优化原理与性能，并与已有的libm算法库和处理器提供的sqrt指令进行了比较，其总体性能是有优势的。针对平方根函数的实现主要是运用了SIMD NEON语言，在ARM架构上进行并行化，之所以使用这项技术一方面是由于ARM架构在市场上的需求逐渐提高，构建ARM架构完整的软件生态十分重要，另一方面是由于目前SIMD技术的重要地位。所以，基于ARM架构的函数开发是很有价值的。而今后的研究工作并不会只局限于本文中的平方根函数，接下来会继续研究反三角函数、三角函数等其他函数的开发。