计及网络重构的多变电站协同优化方法

臧 谦，胡文平，杨少波，孟 良，梁纪峰，柴园园

（1.国网河北省电力有限公司电力科学研究院，石家庄 050011；2.智能电网教育部重点实验室（天津大学），天津 300072）

随着分布式光伏在配电网中渗透率的提高，配电网从被动单向的配电网络转变为功率双向流动的有源网络，并面临潮流倒送和电压越限等安全运行风险[1]。在此背景下，研究配电网的优化调度策略、控制配电网中的无功调压设备和分布式光伏以及网络重构成为系统优化运行的重要手段[2]。

配电网无功优化方法多以网络有功损耗最小为目标建立无功潮流优化模型，利用数学规划算法或人工智能算法（如遗传算法[3]）求解无功调压设备的最优调度策略。文献[4]建立了基于支路潮流形式的配电网三相无功优化模型，并利用二阶锥松弛将原始优化模型转化为具有凸可行域的数学规划形式，对连续、离散无功补偿装置和分布式电源的无功功率进行优化调度。为满足含高渗透率分布式电源配电网的电压控制需求，有功-无功联合优化模型[5]被相继提出，实现配电网网络损耗最小和分布式电源利用率最大的综合目标。文献[6]建立了辐射状配电网有功-无功协调动态优化模型，将分布式电源出力、储能装置充放电功率以及电容器组投切等作为决策变量，最小化配电网的有功损耗。因配电网的最优潮流模型属于非凸NP难题，二阶锥松弛、半定规划松弛[7]和直流潮流约分[8]常被用于凸化最优潮流模型。

有载调压变压器OLTC（on-load tap changer）作为一种有效的电压调节手段，也常被纳入配电网最优潮流模型中。然而，OLTC的数学模型将为配电网最优潮流模型带来新的非凸、非线性约束而难以高效求解[9]。文献[10]提出了一种OLTC模型的线性化处理方法，可将含OLTC的配电网最优潮流模型转变为混合整数二阶锥松弛模型。

网络重构是优化配电网的一个重要措施，通过改变分段开关和联络线开关的组合状态，能够达到降低网损、消除过载、故障恢复、改善电能质量等目的。文献[11]以网络损耗最小为目标，建立了配电网重构的混合整数凸优化模型，并采用分支定界算法进行求解。文献[12]提出一种基于自适应二阶段鲁棒优化方法的三相不平衡配电网的动态重构方法，以减少开关费用和配电网运行成本为目标，并采用列与约束生成算法求解所提二阶段鲁棒动态重构模型。

配电网最优潮流方法虽已取得一定的研究成果，但很少考虑变电站无功调压设备、分布式电源以及联络线开关的联合优化调度。尤其是针对通过联络线开关互联的多变电站协同优化问题，目前鲜见有文章报道。本文以变电站为控制单元，首先建立单变电站的日前优化调度模型，然后提出多变电站协同优化调度策略，考虑利用站内OLTC、并联电容器组、分布式光伏和站间联络线开关的优化调度，实现多变电站的全局经济优化运行，并解决配电网的安全运行问题。

1 单变电站优化调度模型

单变电站的优化调度模型以网络日运行成本最小为目标，求解站内OLTC档位、电容器投切组数、分布式光伏有功和无功输出功率以及馈线开关状态等决策变量的最优解，实现本变电站的安全与经济运行。

1.1 目标函数

变电站优化调度模型的目标是最小化每日网络有功损耗成本，光伏有功发电损失成本，以及OLTC、电容器组和馈线开关等离散设备的动作成本之和，即

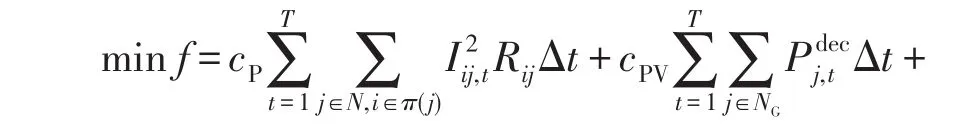
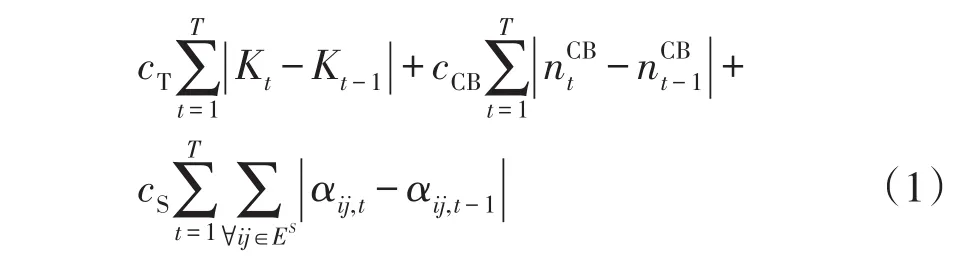
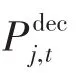
1.2 配电网运行约束

（1）支路潮流等式方程为

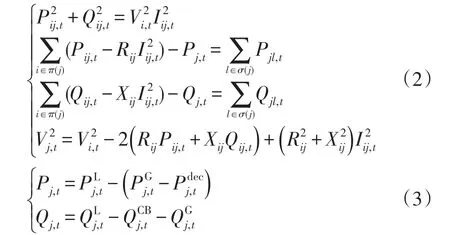
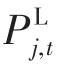
（2）配电网安全运行约束为

式中：Vmin和Vmax分别为节点电压的安全运行下限和上限；Iij,max为支路ij的最大传输电流。

（3）有载调压变压器的运行约束为

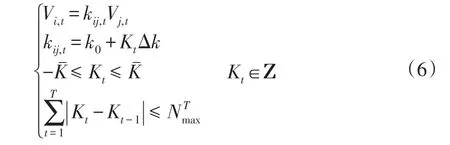
式中：kij,t为支路ij上OLTC的可调变比；k0和Δk分别为OLTC的标准变比和调节步长；为OLTC上调或下调的最大档位；为优化调度时间段内OLTC的最大动作次数。

（4）并联电容器组的运行约束为

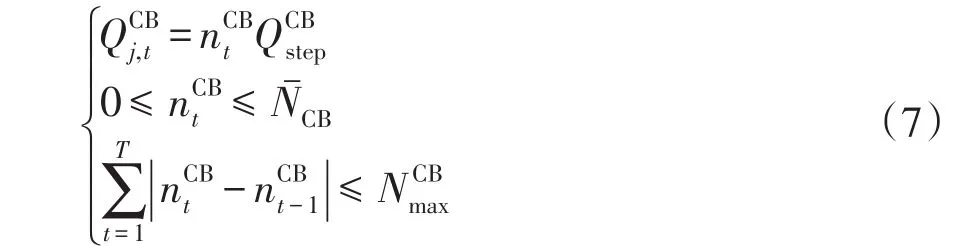
（5）分布式光伏的运行约束为

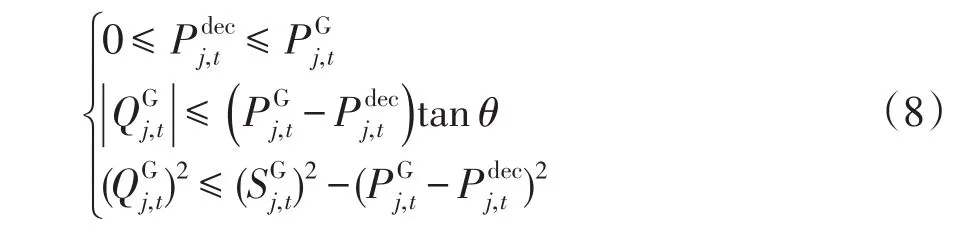
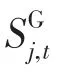
（6）馈线开关的运行约束为

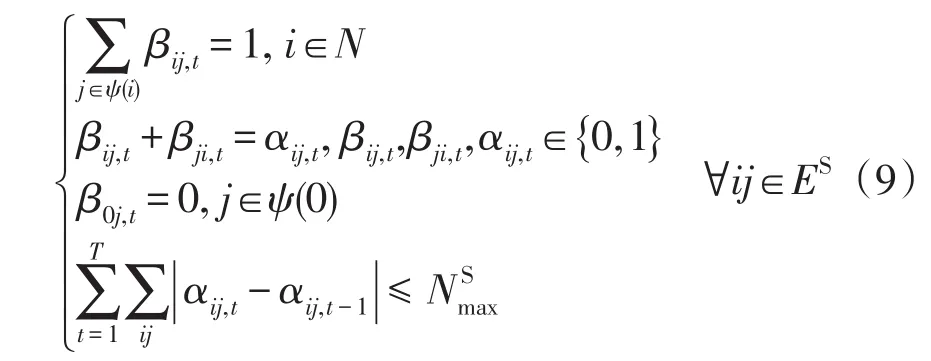
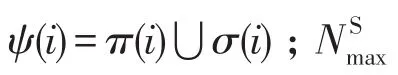
（7）开关支路的电流和电压约束为

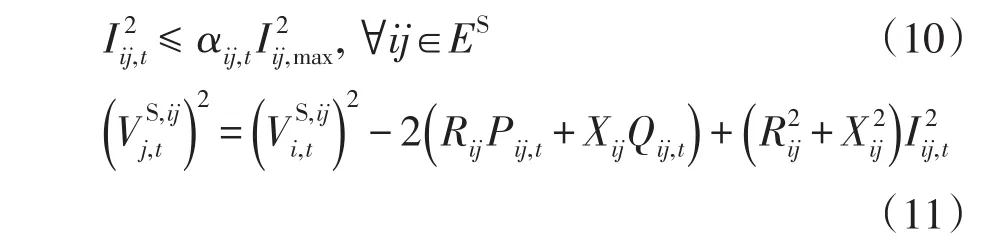
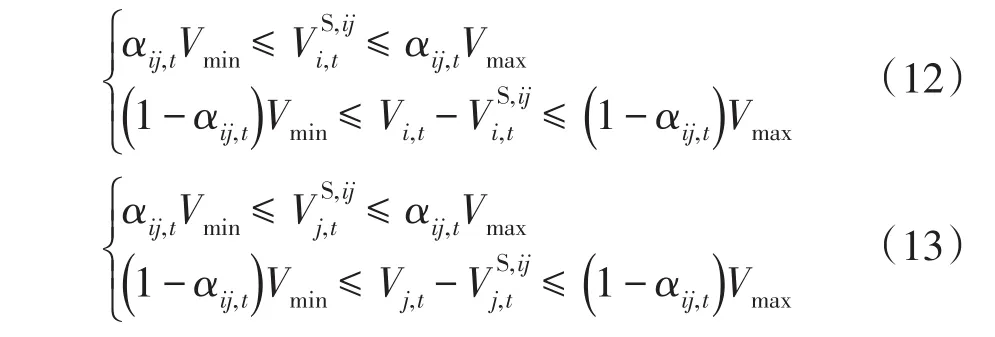
2 模型凸化方法

在单变电站优化调度模型中，式（1）、（2）和（6）存在绝对值项、变量平方项和变量乘积项，使得变电站优化调度模型非凸非线性而难以求解。本文采用变量替换、二阶锥松弛和线性化处理，将变电站优化模型转化为电压平方项vj，t和电流平方项lij，t的混合整数二阶锥优化模型。

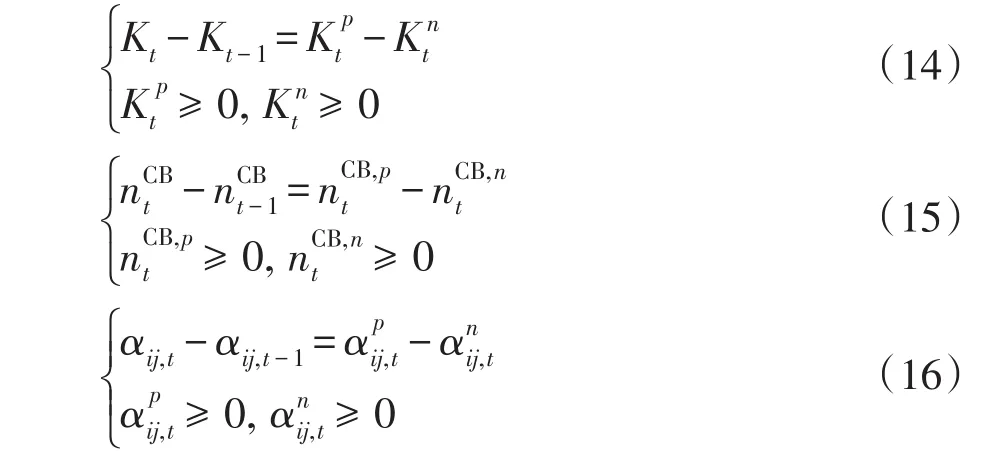
经过等价变形，式（17）可写成如下标准二阶锥形式：

经过变量替换和二阶锥松弛，单变电站优化模型的目标函数和支路潮流方程可转变为如下形式：

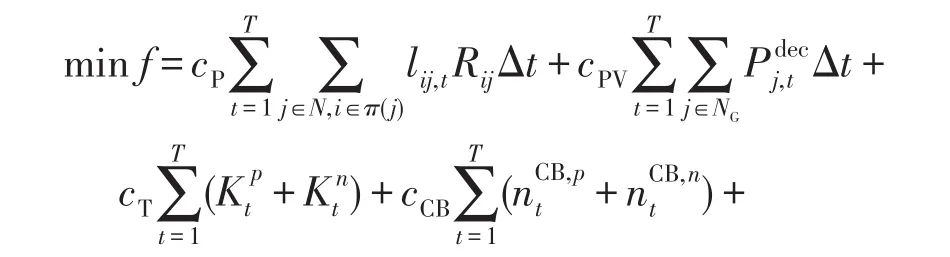
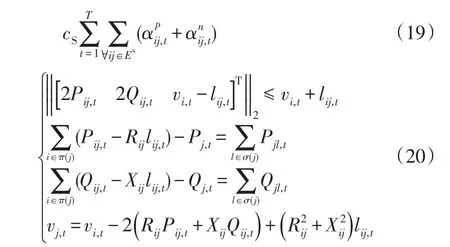
本文进一步引入二进制变量bij,k,t来表示OLTC处在每一档位的状态，则OLTC的运行约束可转化为

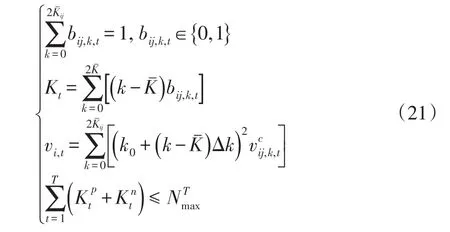
经过以上处理方法，变电站优化调度模型的目标函数为式（19），运行约束包括：式（3）、（7）～（16）以及（20）～（24）。

3 多变电站协同优化方法

图1所示为通过一个联络线开关互联的两变电站简单示意图。本文以图1所示的两互联变电站为例，介绍多变电站的协同优化方法。

图1 两互联变电站的简单示意Fig.1 Schematic of two simply interconnected substations

两变电站的协同优化模型除各变电站的站内优化模型外，还包含两变电站间的边界耦合约束。变电站间的边界耦合约束主要包括边界联络线的传输电流和功率等式约束、边界节点电压等式约束以及站间联络线开关耦合约束，分别如式（25）～（27）所示。

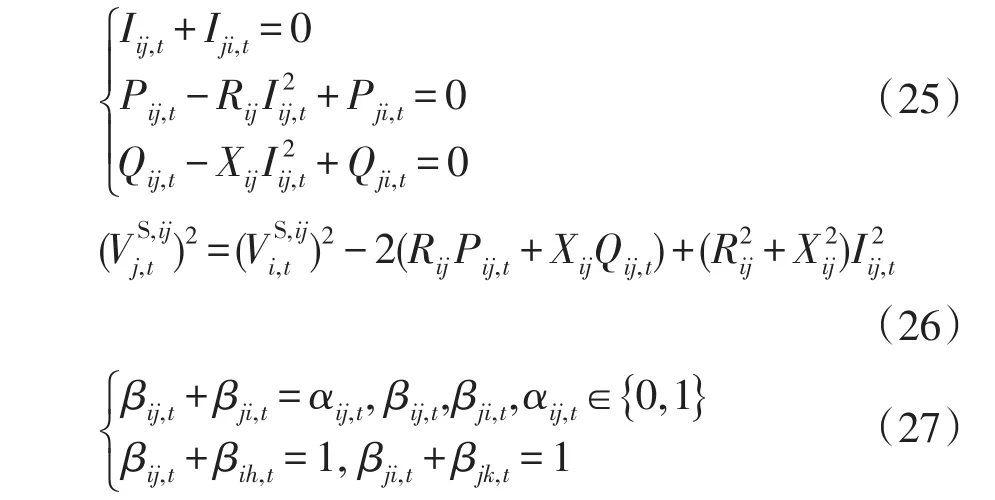
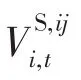
为实现两变电站的协同优化调度，两变电站的控制系统可首先交互两站互联支路的网络参数和负荷数据，并由其中一个控制系统开展互联支路的潮流优化计算，求得最优的开关动作策略。然后基于优化确定的互联支路开关状态，两变电站的控制系统开展站内潮流优化计算，求得本站OLTC、电容器组、分布式光伏以及站内开关的调度策略。

为提高两变电站协同优化的计算效率，两变电站可基于各支路的互联情况，对两变电站互联系统进行简单分区，然后分区开展互联支路的协同优化计算，确定互联支路上的最优开关策略。

4 算例分析

以图2所示的配电系统为例，两变电站互联支路包括B1-B3和B7-B11。根据这些支路的互联情况，B1、B7和B8支路可组成一个分区，而B2、B3和B9-B11可组成另一个分区。

4.1 仿真算例

本文以中国某地实际配电系统为案例进行算例分析，对本文所提出的多变电站协同优化方法进行仿真验证。本文利用Matlab R2013a环境下的CPLEX12.6.3算法包[13]对变电站的日前优化调度模型进行优化求解。该配电系统的网络拓扑结构如图2所示。该系统的网络阻抗参数和节点负荷数据可参见文献[14]。该配电系统共包含11条11.4 kV馈线，本文假定由两座变电站联合供电，两变电站的入口母线电压等级为110 kV，OLTC的电压调节范围均为1±4×1.25%，日最大动作次数设为4。两变电站内的并联电容器组均为10组，单组容量为0.5 Mvar，日最大动作次数设为20。该系统的日峰值负荷功率为28.35 MW+j10.35 Mvar，基准电压和基准容量分别为11.4 kV和1 MV·A。变电站1供给6条馈线上的46个负荷节点，共包含12个分段开关和5个站内联络线开关。变电站2供给5条馈线上的37个负荷节点，共包含13个分段开关和1个站内联络线开关。两变电站通过5个站间联络线开关T1～T5互联。假定两变电站共10个节点装有分布式光伏，安装位置如图2所示。其中，馈线B1、B5和B11上的分布式光伏安装容量均为3 MV·A，而其他馈线上的分布式光伏安装容量均为2 MV·A。系统总负荷和光伏总有功功率一天24 h的变化情况如图3所示。

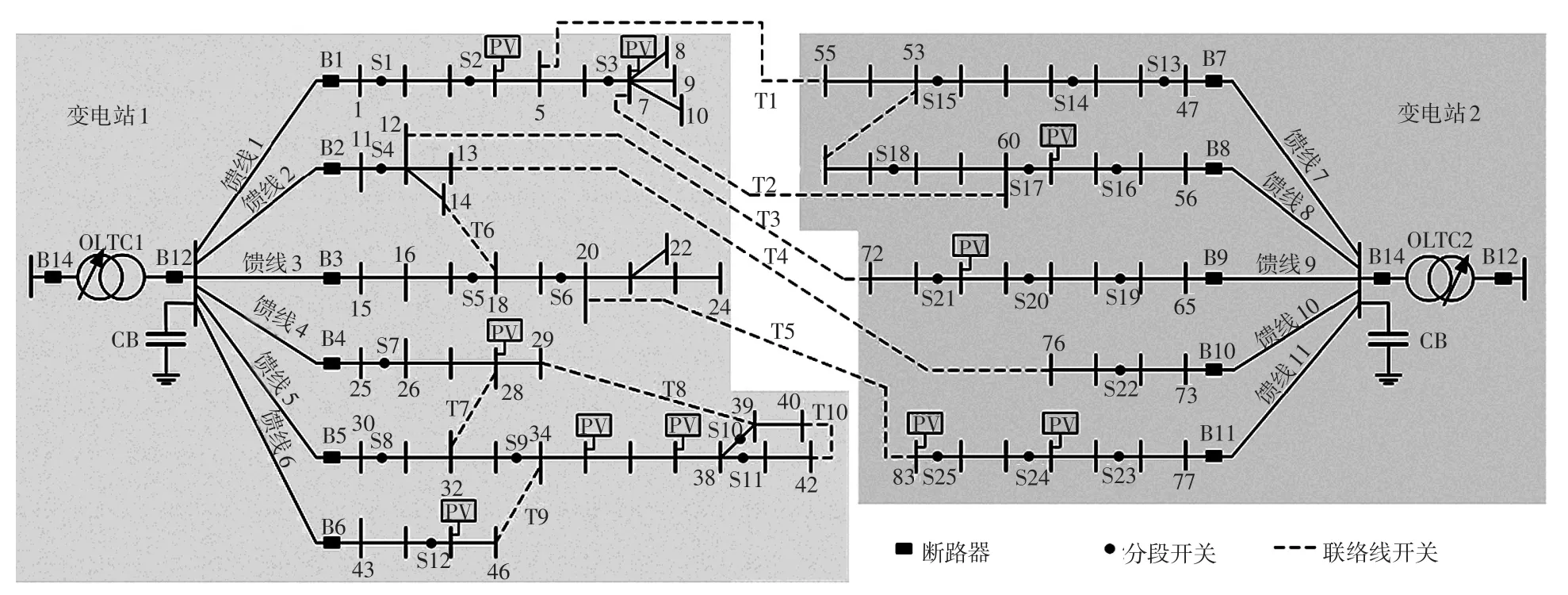
图2 中国某地实际配电系统拓扑Fig.2 Topology of a practical distribution system in China

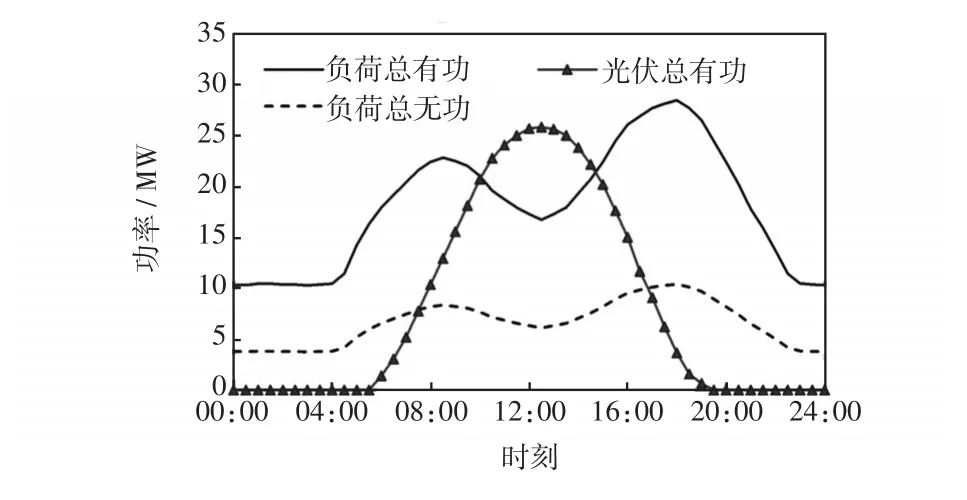
图3 系统内总光伏和负荷日运行曲线Fig.3 Daily curves of total PV power generation and load in the system

本文设定两变电站入口母线电压的标幺值为1.05p.u.，电压安全运行上、下界分别为Vmax=1.05p.u.和Vmin=0.95p.u.；光伏有功缩减成本cPV=700¥/(MW·h)，网络有功损耗成本cP=400¥/(MW·h)，有载调压变压器的单次动作成本cT=30.15¥/次，电容器组投切成本为cCB=1.39¥/次，分段开关和联络线开关的单次动作成本均为cS=5¥/次。该系统开关的初始状态为所有分段开关均闭合而所有联络线开关均断开。

4.2 多变电站协同优化结果

当两变电站开展站内协同优化计算时，变电站1将B1支路的网络参数、负荷和光伏的功率预测数据发送给变电站2，而变电站2将B9～B11这3条支路的网络参数、负荷和光伏的功率预测数据发送给变电站1。然后，变电站1对支路B1～B6以及支路B9～B11进行日前优化调度，确定站间联络线开关T3～T5的最优动作对；而变电站2对支路B7～B11以及支路B1进行日前优化调度，确定站间联络线开关T1～T2的最优动作对。最后，两变电站分别基于求得的站间联络线开关最优动作对，开展站内日前优化调度，求得两站OLTC、电容器组、分布式光伏以及站内联络线开关每30 min的调度策略。

多变电站协调优化时，光伏各时段的无功输出功率如图4所示。在光伏发电时段，大部分节点的光伏作为无功电源，通过输出感性无功来降低网络有功损耗。在正午时段，因光伏安装节点37的电压幅值过高，所以该节点的光伏通过吸收感性无功来避免过电压。

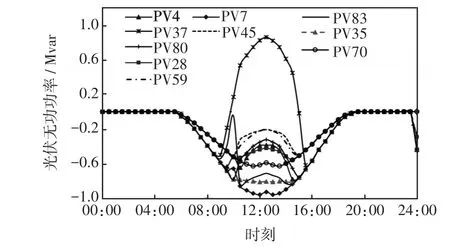
图4 系统内各光伏的无功输出功率曲线Fig.4 Curves of output reactive power from multiple PVs in the system

多变电站协调优化时，两变电站各时段的电容器投入组数如图5所示。在负荷重载时段，两变电站通过投入电容器供给无功功率来降低系统网络损耗。

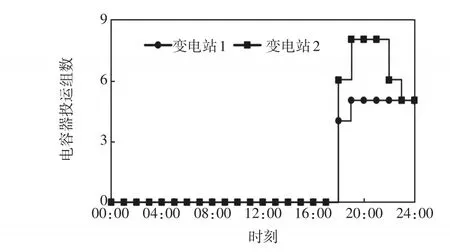
图5 两变电站电容器的投运组数Fig.5 Operation numbers of capacitor banks in two substations

多变电站协调优化时，在一天24 h内系统仅需在两个时刻对分段开关和联络线开关进行操作。在上午10：30时刻，系统开关动作对为：闭合联络线开关T1而断开分段开关S14、闭合联络线开关T5而断开分段开关S24。在下午16：00时刻，系统闭合分段开关S14而断开分段开关S2。其他时刻开关状态保持不变。

多变电站协调优化时，系统网络损耗、离散设备动作次数以及系统日运行总成本等如表1所示。网络有功总损耗为5.95 MW·h，OLTC档位无需调节，电容器共动作16组，光伏有功缩减量为零，开关共动作6次，系统日运行总成本为2 433.62¥。

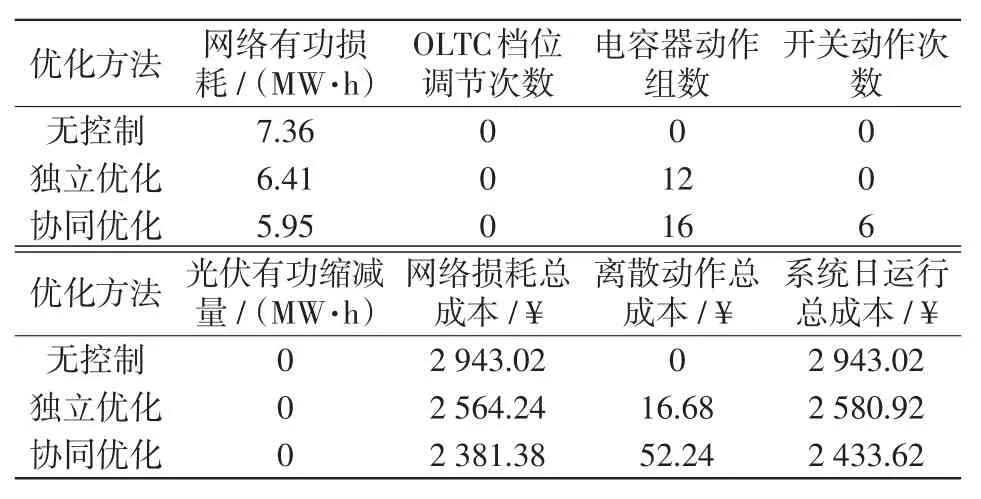
表1 不同优化方法的计算结果Tab.1 Calculation results obtained using different optimization methods

本文进一步对比了无控制和两变电站独立优化时的计算结果，如表1所示。无控制时，两变电站的网络有功损耗共为7.36 MW，系统日运行总成本为2 943.02¥。当两变电站开展站内独立优化计算而无协调时，网络有功损耗降为6.41 MW，两变电站电容器共动作12组，OLTC档位和开关状态均无需调节，系统日运行总成本为2 580.92¥。

无控制、两变电站独立优化以及协同优化时系统各时段的电压峰谷标幺值如图6所示。无控制时，该配电系统存在低电压问题，且在重载时段，系统电压峰谷值之差较大。独立优化和协同优化方法均能有效解决系统的低电压问题，并通过无功补偿减小网络损耗和系统电压峰谷值之差。此外，协同优化方法通过站间联络线开关的优化调度，能够促进分布式光伏的发电功率就近消纳，从而进一步降低网络损耗和日间系统电压的峰谷差。

图6 不同方法下系统电压的峰谷值Fig.6 Maximum and minimum values of system voltage obtained using different methods

由仿真结果可知，相较于无控制，两变电站独立优化方法通过无功功率补偿，能够大幅降低两变电站的网络损耗成本并解决低电压问题。两变电站的协同优化方法利用站间联络线开关的优化调度，能够促进分布式光伏发电功率的就近消纳，进一步降低系统网络损耗总成本。

5 结语

本文首先建立了单变电站的日前优化调度模型，对OLTC、电容器组、分布式光伏和馈线开关进行优化调度，并采用二阶锥松弛等技术对优化模型进行凸松弛，然后提出了一种多变电站的协同优化方法，通过站间协同优化确定站间联络线开关状态，最小化多变电站的总运行成本。最后，利用中国某地实际配电系统的仿真结果验证所提出的多变电站协同优化方法的有效性。仿真结果表明，所提多变电站的协同优化方法通过站间联络线开关的优化调度，能够促进分布式光伏发电功率的就近消纳，有效降低高渗透率分布式光伏配电网的总运行成本。