基于农村发展模式分析的中长期负荷预测方法

熊 宁，肖异瑶，姚志刚，钟士元，舒 娇

（1.国网江西省电力有限公司经济技术研究院，南昌 330096；2.华南理工大学电力学院，广州 510641）

在乡村振兴发展战略背景下，农村及农业产业的发展将促进农村用电需求发展，并伴随用电结构的多样性凸显、季节性问题加剧、供电质量要求提高等新阶段下农村用电需求的新特性。在此背景下，现有的电力负荷预测方法已难以适应新时代农村发展需求，因此，需要为农村地区负荷分布预测提供更具适应性的新方法。

电力系统的负荷预测就是依据系统内存储的历史负荷数据，通过一定的研究方法，得出负荷数据的变化规律，并且通过分析数据得出电力负荷与相关因素之间的联系，进而对未来电力负荷进行一个在误差允许范围内的科学预测。

目前，国内外关于电力系统负荷预测方面的研究很多，从传统的单耗法、弹性系数法、统计分析法，到经典的回归分析法[1-2]、时间序列分析法[3-4]、灰色预测法[5-6]和模糊数学法，甚至到现代的神经网络法[7]、优选组合法[8]和小波分析法[9-10]等，不同的预测方法有其不同的适用场景，进而导致预测精度也各不相同。文献[11]使用了广义回归神经网络进行中长期负荷预测；文献[12]针对长期电力需求预测的特点，提出了分段最优灰色系统预测模型；文献[13]基于物元理论建立了电力系统物元模型预测未来负荷变化；文献[14]使用改进的聚类算法对中长期负荷年份进行聚类，在此基础上根据预测年份的属性数据对电力负荷进行预测；文献[15]基于偏最小二乘回归分析的中长期电力负荷预测方法，该方法集主成分分析、典型相关分析和多元线性回归分析于一体；文献[16]采用了应用最大模糊熵模型进行电力系统的负荷预测方法根据历史数据，对各历史年进行分类，并分析得出各类的环境因素特征及负荷增长趋势，通过特征比较得到预测年的负荷曲线。然而，这些方法均是针对城市配电网负荷的预测方法，并未考虑农村负荷的特征。

由于农村缺乏控制性详规，且地区发展易受政策等因素影响，负荷性质、规模及增长趋势缺乏规律，上述方法难以应用于农村地区。张志强[17]将农村电力负荷分为大工业、商业、农业、居民等6类，基于历史负荷数据的分析，用时间序列法对各行业负荷展开预测。黄一凡[18]考虑农村电网对负荷的压制、电网健康程度改善时压制负荷的恢复性增长，提出农村负荷预测新方法。然而，时间序列法是利用过去负荷的规律来推测未来负荷的发展趋势，仅适用于短期预测；电网健康程度改善对负荷恢复性增长的影响更适用于未来1～2年内的负荷预测。因此，针对农村中长期电力负荷预测的研究几乎空白。

在已有研究的基础上，本文考虑了国家政策规划、经济、人口等影响农村负荷变化的因素，提出一种基于农村发展模式的电力负荷中长期预测方法。该方法分为农村发展模式预测模块以及电力负荷中长期预测模块两部分。首先，基于对农村发展模式和农村电力负荷特性的分析，改进了传统的K-means聚类和K近邻算法，提出了K-means-Robust聚类算法和加权自适应K近邻KNN（K-nearest neighbor）算法组成农村发展模式预测模块。在此基础上，针对不同农村发展模式，使用结合了灰色关联度分析的正则化门控循环神经网络方法进行中长期电力负荷预测。算例表明：本文所提算法在实际农村电力负荷数据集上的表现较好，准确率高于长短期记忆LSTM（long-short-term memory）网络、支持向量机SVM（support vector machine）等常见电力负荷预测模型。

1 农村中长期负荷预测基础

由于农村在不同发展模式下具有不同的用电用户类型分布，并且不同类型用电用户也具有不同的用电模式，因此，本文从农村用电数据出发挖掘了不同发展模式下的负荷类型分布，进而对农村不同发展模式进行精细模拟并预测中长期负荷。

1.1 农村用电负荷分类

农村用电负荷是指农村居民日常用电、农业生产用电、工业用电、商业负荷、学校和医院等用电负荷，并且不同的负荷类型具有不同的特点。比如农业负荷受气候、季节、地理等自然条件的影响很大，整体负荷密度较小，这是由农业生产的特点所决定的；居民负荷一定程度上和农业负荷类似，且在傍晚、清晨有用电小高峰期；工业负荷所占的比重较大，其负荷特性受工厂行业的生产周期影响较大。综合来讲，重工业的负荷量大，且需求平稳；轻工业负荷相对较低，且峰谷差较大。同时，由于商业、学校、医院等负荷相对较少，为了简化分析，本文将该类负荷统称为第三产业负荷。

对于电力负荷特性的研究有很多，按照时间可分为年负荷、月负荷和日负荷；而按照数据指标可分为最高利用小时、峰谷差等指标。然而，负荷日变化曲线可以很好地反映用户一天内的行为，因此本文采用负荷的日变化曲线作为负荷特性指标。

1.2 农村发展模式分类

针对农村在不同发展模式下具有不同的用电用户类型分布，以及不同类型用电用户具有的不同用电性质的特点，有必要结合用户用电类型分布和负荷特性，以及影响农村电力负荷变化的因素划分农村发展模式类型。然而，影响农村用电负荷变化的因素有经济、人口、国家政策导向、自然地理条件以及电价等众多因素，因此在分析不同农村发展模式下用电用户负荷类型以及影响因素的基础上，本文主要以经济水平、负荷类型和国家政策导向作为农村发展模式的划分依据，并将农村的发展模式分为以下3类[18]。

（1）农村发展模式1。

以农业生产用电负荷为主的农村发展模式。该类发展模式特征为：农村经济水平不高，发展政策导向不明确，农业用电、居民日常用电负荷占主导地位，且电力负荷波动不明显。

（2）农村发展模式2。

以工业负荷为主的农村发展模式。该类发展模式特征为：农村经济水平较高，发展政策导向较为明确，工业、第三产业用电负荷增加，且电力负荷波动较为明显。其中，发展模式按照发展速度可以划分为中速发展模式和高速发展模式。

（3）农村发展模式3。

以第三产业负荷为主的农村发展模式。该类模式特征为：农村经济水平很高，发展政策导向明确，工业、第三产业用电负荷猛增，且电力负荷波动很明显。

2 农村中长期负荷预测模型

2.1 农村发展模式预测模型

为解决农村用电负荷的分类以及不同农村发展模式的分类问题，本文建立了农村发展模型预测模型。首先，为了更好地利用电力负荷大数据，提出了改进的K-means-Robust聚类模型对农村用电负荷类型进行聚类分析；进而将聚类分析结果与农村电力大数据结合，提出了加权自适应KNN算法实现农村发展模式预测。农村发展模式预测模型流程图如图1所示。

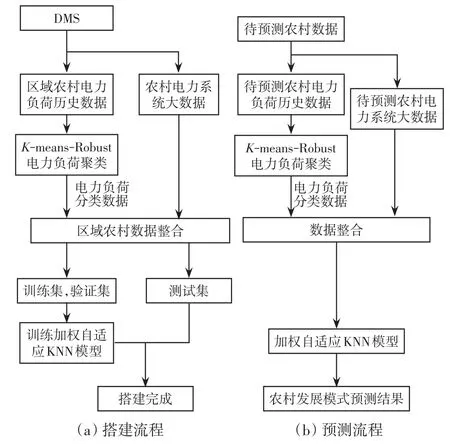
图1 农村发展模式预测模型流程Fig.1 Flow chart of rural development mode forecasting model

2.1.1K-means-Robust农村用电负荷聚类模型

1）K-means聚类算法

K-means聚类算法的核心思想是把每个元素聚集到其最近中心类，使同一聚类中的对象相似度较高，而不同聚类中的对象相似度较小。对于包含n个对象的数据集D={d1,…,dn}，目的是把n个对象分配到k组不同的聚类簇中S={S1,…,Sk}，其目标函数为

式中：S代表聚类结果；Cost(Si)为聚类簇Si中所有数据点到聚类中心的距离平方之和。

2）K-means-Robust聚类算法

虽然K-means算法具较高的准确性且易于实现，但它依赖于初始化中心的选择且受离群点的影响较大。在电力系统背景下，电力负荷的数据量较大且采集样本往往包含大量离群值，因此有必要从速度和鲁棒性角度改进K-means算法。本文在借鉴Elkan[19]提出的利用三角不等式提升K-means聚类速度方法，以及Olukanmi等[20]提出的K-meanssharp方法的基础上，提出了K-means-Robust聚类算法。改进后的K-means使用了三角不等式加速数据点到每个质心距离的计算过程；同时，在更新质心时加入了离群值检测，使得算法具有较好的鲁棒性。因此，本文采用K-means-Robust聚类算法对农村用电负荷进行预测。K-means-Robust聚类算法流程如下。

步骤1随机选择k个数据点作为初始质心。

步骤2计算k个质心间的距离，并使用哈希表保存每个质心到其他质心的最短距离，用d(Ci,Cj)表示，d(a,b)表示数据点a到b的距离。

步骤3遍历每个数据点，如果数据点x不属于任何簇，则将归属到最近的簇中；如果数据点x属于质心Ci所在的簇，且2d(Ci,x)≤d(Ci,Cj)，则数据点x无需变动；否则继续计算数据点x到现有k个质心的距离并将x分配到新的簇。

步骤4重新计算质心，在计算过程中仅使用与当前质心距离在3个标准偏差内的点进行计算，更新公式为

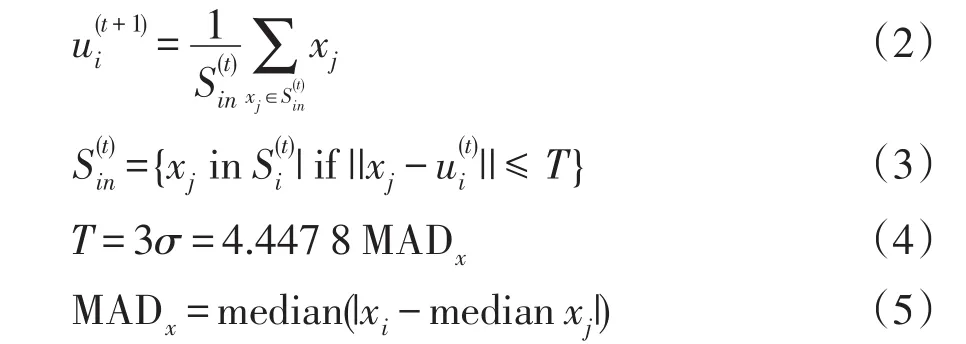
式中：xj为某一数据点；S(t)in为参与质心更新计算的数据点集合；σ为样本分布的标准差；T为参与质心更新的阈值；MADx为每个点到中值点的距离组成的所有数据的中值点。

步骤5重复步骤2～4直至所有质心不再变动。

2.1.2 加权自适应KNN算法

KNN算法是一种机器学习领域常用的分类算法。由于KNN理论较为成熟，实现方法简捷，能对复杂的决策空间有效建模，被广泛用于各个领域。KNN算法的3个基本要素为：k值的选择、距离度量及分类决策规则，其中分类决策规则通常是多数表决。

然而，在电力系统大数据背景下，运用传统KNN算法预测农村发展模式会导致较大预测误差，原因在于农村各维度特征对于农村发展模式的影响程度不同，同时人工选择的k值容易导致模型过拟合。因此，本文提出了加权k值自适应KNN算法，该算法对样本的每一维特征加权，并使用梯度下降法优化求解权重向量；同时，遍历搜索k值得到最优解。加权k值自适应KNN算法的目标函数为

式中：yi为数据点i的类别值；y′i为数据点i的预测值；n为训练样本数量。

加权k值自适应KNN算法流程如下：

步骤1在设定的取值空间内遍历k值，对于每一个k取值，重复步骤2和步骤3；

步骤2使用梯度下降法求解权重矩阵；

步骤3使用测试集测试模型性能并记录；

步骤4根据测试集上的模型性能表现确定最优k值及权重矩阵，性能度量指标使用所有类的平均准确率（mean precision）来度量。

相较于传统KNN算法，本文提出的加权k值自适应KNN算法在农村发展模式预测任务具有更高的准确率。

2.2 基于农村发展模式的负荷预测模型

针对不同农村发展模式下影响用电负荷变化因素不同的问题，本文采用灰色关联分析方法对农村的具体发展模式下负荷数据进行分析，得到该发展模式下不同影响因素与用电负荷的关联度，进而确定具体影响农村负荷变化的主要因素，并作为门控循环神经网络预测模型的输入。

2.2.1 灰色关联分析

采用灰色关联分析方法计算影响负荷变化的主要控制因素和其余因素的影响权重，计算过程如下。

步骤1各输入属性归一化处理。对农村不同类型的负荷分布、人口、经济、地理位置以及国家发展政策等信息进行归一化处理，计算公式为

步骤2关联系数计算。关联系数是比较变量间相似程度的参数，关联系数越大，代表变量间关联程度越大。关联系数计算公式为

式中：ε0ij(k)为关联系数；Δ为同一输入属性在k时段内的差值绝对值；ρ为分辨系数。

步骤3将大量关联系数信息通过求取平均值的方式进行耦合，得到总体的量化关联结果。关联度计算公式为

式中：ζ0ij为关联度；N为输入属性序列长度。

通过上述灰色关联度的分析计算，可以得到各变量与负荷变化的关联度及相关变量之间的耦合程度，并忽略次要因素，得到主要因素。

2.2.2 正则化门控循环神经网络负荷预测模型

随着深度学习的飞速发展，循环神经网络RNN（recurrentneuralnetwork）因为拥有较好的拟合能力被广泛应用于时间序列预测问题。考虑到电力负荷数据具有时间序列属性，本文使用深度学习中性能较强的门控循环单元GRU（gate recurrent unit）网络来进行电力负荷预测。GRU神经网络是对LSTM网络的改进网络，GRU网络内部信息流程如图2所示。

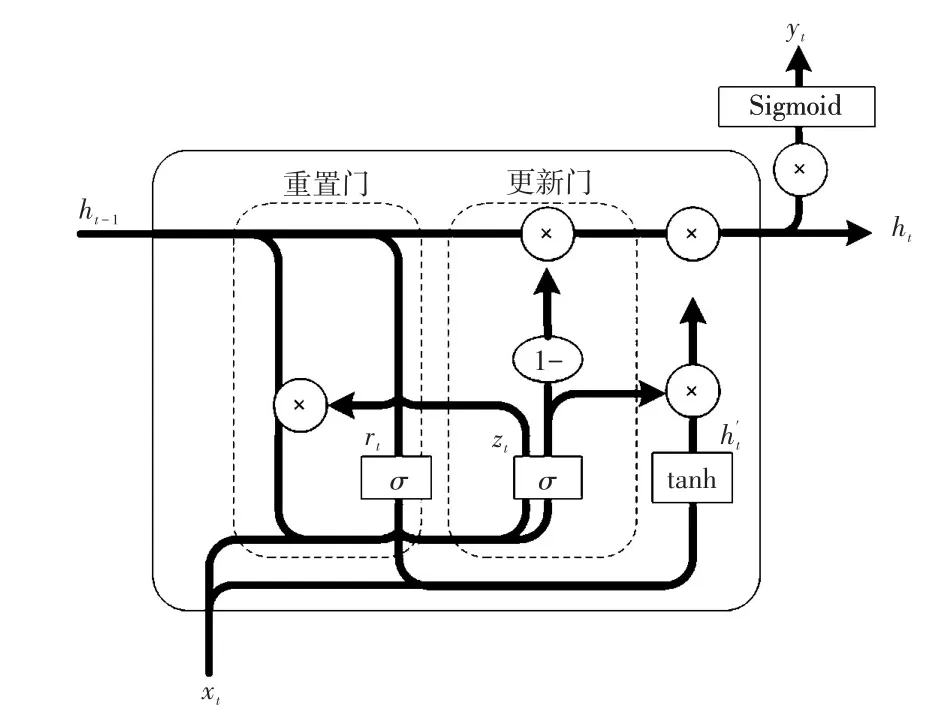
图2 GRU网络内部信息流程Fig.2 Flow chart of internal information of GRU network

与LSTM网络相比，GRU网络更为精简。GRU网络中舍去了细胞状态，同时把LSTM内部的3个门控单元简化为两个，分别是重置门和更新门。重置门负责控制有多少前一状态的信息需要保留，更新门负荷控制要舍弃哪些信息以及要添加的新信息。其中，zt确定是否要将当前状态与先前的信息结合起来，而rt表示需要保留多少信息。GRU单元的更新公式为

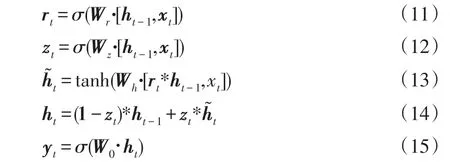
式中：[]表示两个向量相连；*表示矩阵的乘积；σ为sigmoid函数；ht-1、ht分别为t-1、t时刻GRU单元的隐藏状态向量；zt为t时刻更新门中间状态向量；Wz为更新门权重矩阵；rt为t时刻重置门中间状态向量；Wr为重置门权重矩阵；Wh为控制隐藏状态更新的权重矩阵；为t时刻隐藏状态的备选向量；tanh为双曲正切激活函数；yt为t时刻模型输出；W0为输出层权重矩阵。

网络训练中使用均方误差MSE（mean-squared error）损失函数，即

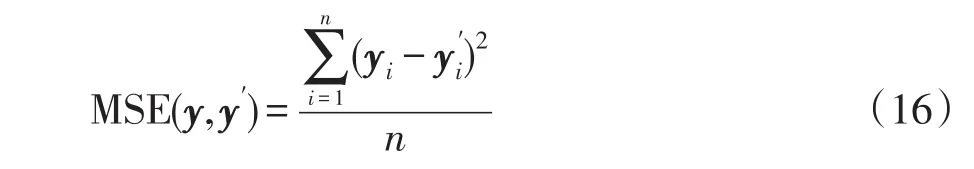
在模型的训练阶段，如果使用单样本梯度下降法优化参数，模型容易受到个别异常样本的影响。另一方面，由于模型的深度需要人工调参且通常为了避免过拟合选择较浅的深度，直接使用式（16）的损失函数在一定程度上影响了模型的准确率。因此本文使用了两种正则化方法优化GRU模型，即在模型的训练阶段使用小批量方法训练模型，并在模型的代价函数中加入模型的权重惩罚项，使得模型有效地避免过拟合，提高了模型泛化能力。

改进后的正则化GRU模型单次迭代的损失函数为

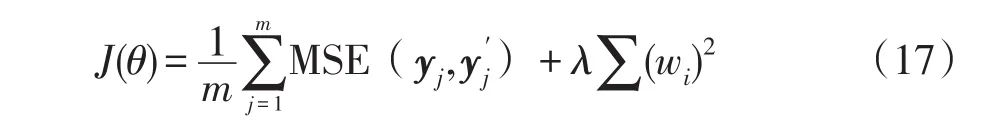
3 农村中长期负荷预测方法

本文在考虑农村负荷特性以及发展模式的基础上，既考虑了国家政策规划，也考虑了农村实际自然地理条件，提出了一种基于农村发展模式的电力负荷中长期预测方法。农村中长期负荷预测方法流程图如图3所示。

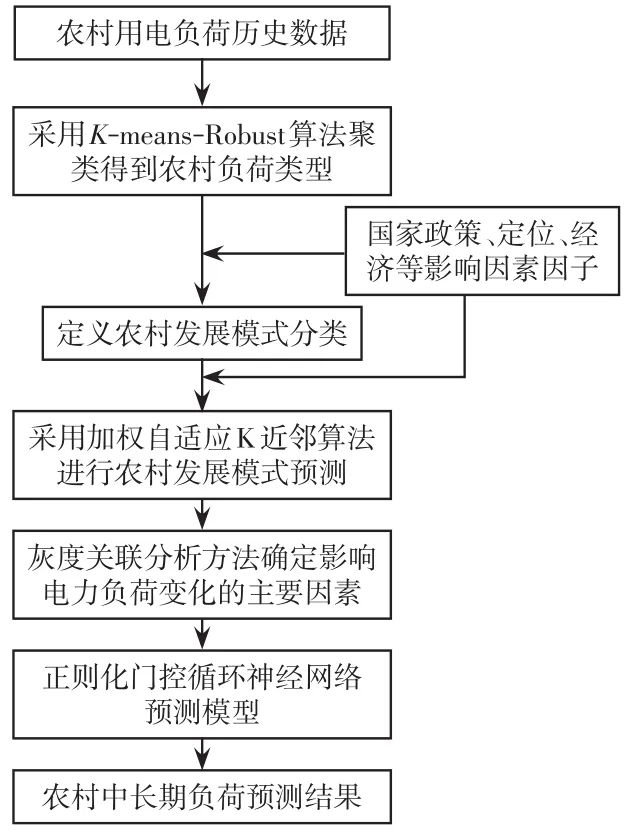
图3 农村中长期负荷预测流程Fig.3 Flow chart of medium-long-term load forecasting in rural areas

4 算例仿真

本文选取中国江西省某地区300个自然农村2016—2018年的历史电力负荷数据作为算例。电力负荷数据的采集间隔为15 min，即每一天包含96个采集时间点的负荷值。为了验证本文提出的预测方法，对该农村采集的数据包括：①农村电力负荷历史数据；②农村人口分布情况；③农村GDP历史数据；④农村自然条件数据，如海拔、温度、离县城中心距离、离二级高速路距离等；⑤农村发展规划，即工业园区规划、农业主导规划、第三产业规划如旅游业规划；⑥农村发展结果标签数据，即某一农村3年发展结果，分为以农业为主导、以工业为主导及以第三产业为主导。

首先，将所采集的农村大数据各维数据归一化，采用K-means-Robust聚类分析得到所有农村的电力负荷类型分布，并将每一类负荷值作为某一农村的一维特征。然后将电力负荷类型分布数据与上述采集的农村数据结合进行整合，以6∶3∶1的比例切分所有数据集为训练集、验证集和测试集。使用训练集和验证集训练加权自适应KNN模型，并使用测试集确定最佳的模型参数。基于农村发展模式的预测结果，对于3种不同的发展模式，分别使用灰色关联分析确定该发展模式下影响农村发展的主要成分，并训练对应的多维GRU模型。最后，对于待预测农村，利用训练好的农村发展模式预测模型和GRU模型对农村电力负荷进行中长期负荷预测。

4.1 电力用户类型聚类分析

算例中K-means-Robust聚类分析使用的数据为100个农村的2017年6月到2018年12月的历史日用电负荷数据。将每一天的日用电负荷数据作为一个样本，对每个农村的日用电数据随机采样10次，取10次聚类的平均结果作为聚类结果。为了避免K-means-Robust需要手动设置类别数而使聚类结果受先验知识影响，在聚类前使用Canopy聚类得到合适的聚类类别数。Canopy聚类是一种特殊的聚类算法，其特点是不需要人为设置聚类的类别数k值，对噪声的抗干扰能力较强，但聚类准确度略低于K-means-Robust。某农村电力负荷的Canopy聚类的结果如图4所示。

图4 电力负荷分类Canopy聚类结果Fig.4 Canopy clustering results of power load classification

由图4聚类结果可知，Canopy聚类出了3个相对独立的电力用户类别。因此，设置k值为3，使用K-means-Robust对农村大数据再次聚类分析，得到的聚类中心曲线如图5所示。

由图5可知，不同电力负荷的变化特点如下：

图5 电力负荷分类聚类结果Fig.5 Clustering results of power load classification

（1）第1类负荷有两个高峰用电区间，分别为07：00—12：00和17：00—22：00，且平均用电量较低，推测此类负荷为农村居民用电负荷。

（2）第2类负荷的特点是24小时内的平均用电量较高，相较于其他负荷在0：00—06：00和21：00—24：00仍保持较高用电量，推测此类负荷为工业用电负荷。

（3）第3类负荷的用电区间跨度较大，07：00—18：00间的用电较为稳定，且高峰期为18：00—21：00，推测此类负荷为第三产业用电负荷。

4.2 农村发展模式预测模型

对300个农村的历史用电负荷分别使用K-means-Robust聚类分析，得到历史用电负荷类型分布，进而计算出4种负荷的年用电量。在此基础上，结合采集的多维农村数据训练加权自适应KNN模型，并以kd树的格式储存农村发展模式数据。300个农村数据中，农业方向发展模式的有234个，工业方向发展模式的有19个，第三产业方向发展模式的有47个。其中，10个农村的相关数据见表1，将发展规划和发展结果数值化为0～3，分别代表没有规划方向、农业发展方向、工业发展方向以及第三产业发展方向。

表1 10个农村的相关数据Tab.1 Related data of ten rural villages

由表1中可知，政府的发展规划对于农村的发展方向有较大影响，并且不同发展方向的农村用电特性也有较大差异，相同发展方向的农村用电特征较为相似。对于待分析农村，使用K-means-Robust聚类分析得到三类产业的用电负荷，再与其他农村数据合并为特征向量。最后，使用训练好的KNN模型得到该农村的发展结果预测。

4.3 基于灰色关联分析的正则化GRU负荷预测模型

基于第1.2节中的发展模式分类，利用灰色关联分析算法分析该模式下影响电力负荷的主要因素，对农村电力大数据降维处理。对于不同发展模式的农村，使用灰色关联分析计算历史负荷数据与其他变量数据的灰色关联度，取所有该发展模式下农村的灰色关联度平均值如表2所示。

表2 不同发展模式下农村大数据灰色关联度统计Tab.2 Statistics of grey relevance degree of rural big data in different development modes

由表2可知，取各发展模式下与负荷灰色关联度高于0.5的变量作为用于预测负荷的数据，搭建并训练相应维度的GRU负荷预测模型，如：对于以第三产业为主的农村发展模式，取GDP、温度、电价时间序列数据和历史负荷数据作为GRU的输入，训练GRU模型。

将待预测农村2016—2018这3年的所有数据进行归一化处理，并以8∶2的比例切分训练集和测试集。在训练过程中，选用批量梯度下降法训练模型，批量设置为64，训练周期设置为15。算例中比较了包括SGD、RMSP、Adam等优化器，测试结果表明Adam优化训练的模型准确率最高。

为验证本文提出预测方法的预测性能，在实验中使用了普通GRU模型（不考虑农村发展模式）、LSTM和SVM作为对比模型，本文提出的基于农村发展模式的正则化GRU预测模型命名为Improved GRU。以某一个第三产业为主发展方向的农村负荷为例，各预测模型在测试集上的预测结果如图6所示。各预测模型在测试集上的性能用均方根误差RMSE（root-mean-squared error）和标准均方根误差 NRMSE（normalized root-mean-squared error）度量，如表3所示。

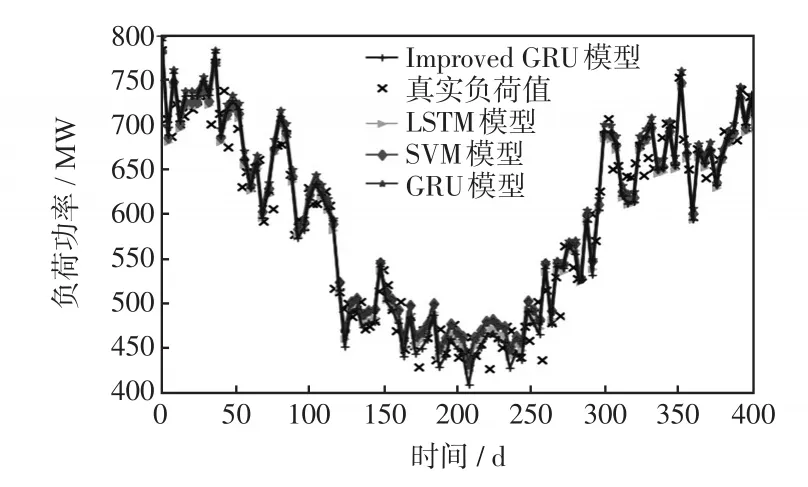
图6 GRU负荷预测曲线Fig.6 Load forecasting curves of GRU

由表3可知，SVM模型在测试集上的表现最差，Improved GRU模型在测试集上的预测误差最小，普通GRU模型和LSTM模型的预测误差相差不大。因此，本文所提出的负荷预测模型对于农村中长期电力负荷预测任务具有较高准确率。

表3 负荷预测模型性能比较Tab.3 Comparison of performance among load forecasting models

为实现电力负荷中长期负荷预测，将GRU模型的预测输出加入到下一个时刻输入向量中，从而实现电力负荷迭代预测。以第三产业为主发展的某农村迭代预测曲线如图7所示。

图7 某农村中长期负荷预测曲线Fig.7 Medium-long-term load forecasting curve of one rural area

5 结语

本文提出一种基于农村发展模式的中长期负荷预测方法，该方法考虑了影响农村负荷变化的经济、人口、国家政策规划等影响因素，提出了K-means-Robust聚类算法和加权自适应KNN算法，搭建了农村发展模式预测模型。在此基础上，利用灰色关联分析法挖掘不同农村发展模式下影响负荷变化的主要特征，并利用主要特征训练正则化的深度门控循环网络，从而实现农村中长期负荷预测。在预测过程中，考虑了符合农村发展实际的各方面因素，且考虑了农村不同的发展模式，使得农村负荷预测结果更准确、更切合实际。