基于低秩矩阵与稀疏约束的运动模糊图像盲复原
2021-05-11鱼轮韩美林
鱼轮,韩美林
(商洛学院电子信息与电气工程学院,陕西商洛 726000)
在数字成像设备采集图像过程中,由于设备的抖动、散焦等因素,获取的图像不可避免的会出现一定程度的模糊[1]。假设模糊是均匀的,则这一过程可以表示为:y=x⊗h+n,其中,x和y分别为原始清晰图像和退化图像,h为模糊核,⊗表示卷积运算,n为加性噪声。图像复原研究的是如何根据模糊图像y恢复出原始清晰目标图像x,这是一个具有病态性质的反问题:给定一张模糊图像,能推测反演出多组模糊核和不同清晰程度的图像[2]。要想高质量的恢复出原始清晰图像,就必须在求解过程中引入关于图像或模糊核的先验知识[3]。现有的先验知识主要集中在清晰图像的先验概率模型上,大致可以分为图像梯度上的先验信息和图像块的先验信息。图像梯度先验信息指的是清晰图像的梯度满足重尾分布的特征,Fergus[4]、Krishnan[5]、Shan[6]、Filip[7]等分别采用高斯混合模型、超拉普拉斯分布、分段函数、重尾分布来近似图像的梯度分布,但由于图像梯度表示的是图像相邻像素之间的关系,能提供的信息有限。图像块表示图像更大的结构上的关系,因此能表征更多的信息。Irani[8]把不同尺度图像间存在的结构自相似性作为先验知识进行图像盲复原,算法的准确性和复原效果有了一定提升。Dong等[9]基于图像非局部相似性满足低秩的特点,提出一种空间自适应迭代奇异值阈值方法进行图像复原。本文提出一种基于低秩矩阵与稀疏约束的运动模糊图像盲复原算法。首先,根据图像非局部自相似的特性,利用低秩矩阵恢复相似块组。其次,构造图像梯度和模糊核的稀疏正则项,将低秩矩阵和稀疏正则化方法结合,建立图像复原模型,通过变量分离策略,交替迭代解决模糊核估计问题。最后,利用非盲解卷积法完成最终的图像复原。
1 图像复原模型
通常假设点扩散函数是空间移不变的,图像模糊模型可简化为目标图像和点扩散函数的卷积过程:y=x⊗h+n,本文在此基础上建立的图像复原模型表示为:

式中第一项为保真项,是图像块匹配后的低秩部分;第二项和第三项分别代表图像梯度和模糊核的正则项约束、β、α为正则参数。图像先验约束项R(x)采用的是图像梯度的L0范数,这样能更好地表示图像稀疏特性,有效保留图像的主要边缘,抑制细小边缘。模糊核约束项采用的是稀疏约束,同时附加非负性约束和能量约束,即:
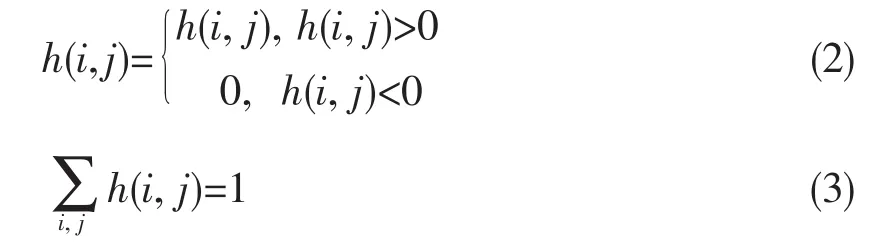
2 算法原理
2.1 模型求解
复原的目标函数可转化为三个子问题,低秩矩阵近似的目标函数式为式(4),最小化图像目标函数式为式(5),最小化模糊核的目标函数式为式(6)。

2.1.1 低秩矩阵目标函数式求解
采用文献[8]中的自适应阈值收缩的奇异值分解法求解。根据文献[8],当p=1,q=2时,‖Ai‖1,2可以表示为矩阵S(yi)的奇异值之和,即:

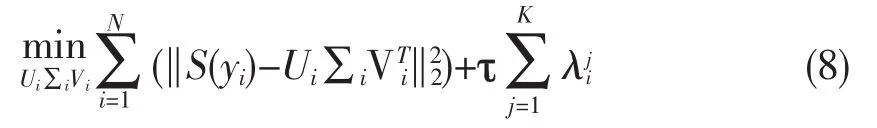
2.1.2 图像目标函数式求解
采用文献[9]中提到的半二次变量分裂最小化方法求解L0范数,引入变量g=Δx,将问题转化为二次凸优化,即:
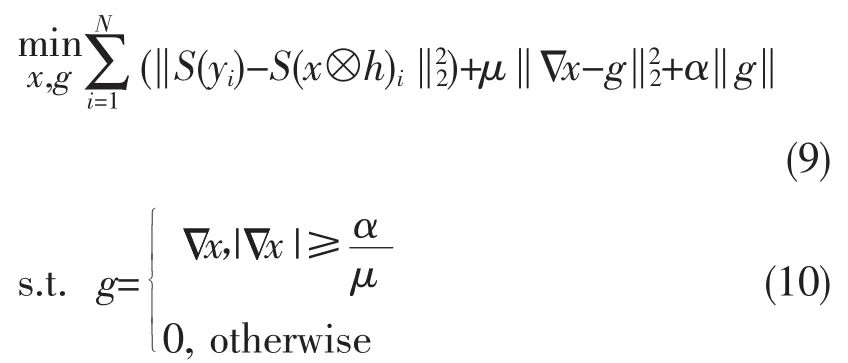
固定其他变量,交替求解x和g。g初始为全零,每次迭代时,x可由式(11)求解:

利用快速傅里叶变化(FFTs)提高求解速度,即:
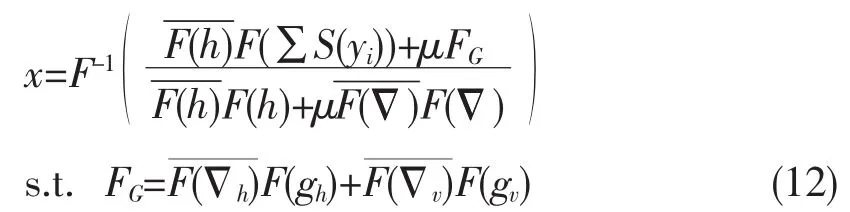
其中,F(·)和 F-1(·)分别为傅里叶正、逆变换,为傅里叶变换后共轭,h和v分别代表水平和垂直方向微分。
2.1.3 模糊核目标函数式求解
固定x,更新模糊核h时,考虑到式(6)灰度条件下的解不够准确[10],转化到梯度空间下。

式(13)同样采用半二次变量分离和FFTs求解。
2.2 算法整体流程
为了精细估计模糊核,本文采用由粗到精的多尺度图像金字塔策略渐进估计模糊核。图像分层采样系数为,具体步骤如下:

当模糊核确定后,再采用文献 [5]中的Hyper-Laplacian先验的正则化法反卷积,获得最终复原结果。
3 实验结果与分析
实验仿真环境为CPU Intel R Core(TM)i5-4210 CPU@2.70GHz,RAM4GB的计算机,使用Matlab R2015b完成实验仿真。客观评价指标上,用峰值信噪比(PSNR)、拉普拉斯梯度模(Laplacian Sum,LS)和灰度平均梯度(Gray Mean Grads,GMG)[11]衡量图像的复原效果。
用于测试本文算法的为Levin的运动模糊数据集[3],图 1(a)、图 1(b)分别为原始图像和模糊图像。对比算法为经典文献[5]、文献[7]、文献[12],各算法复原结果对比图,如图 1(c)、图 1(d)、图 1(e)所示。

图1 各算法复原结果对比图
由图1可知,文献[12]复原视觉结果最差,这是因为文献[12]中使用的Richardson–Lucy算法没有收敛条件,有可能最优解被迭代。文献[5]复原结果虽有所提升,但是复原图像中小女孩的脸蛋、小手处和小男孩的手臂处存在振铃现象。相对于文献[5]和文献[7]的复原结果,本文算法的复原质量有所提升,本文算法能恢复出较多的细节,如本文复原图像中,小女孩的衣服展现出了更多的细节。
另一方面,从实验指标(见表1)来看,本文算法指标均优于其他算法,PSNR、GMG、LS越大,表示图像内容越丰富,细节更好。
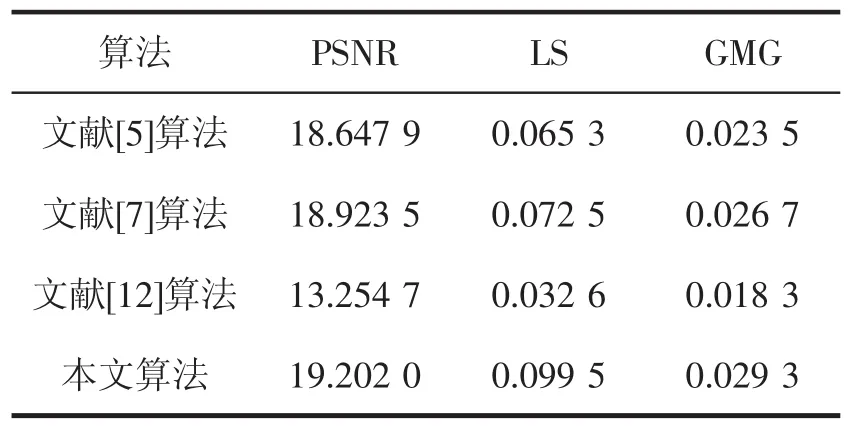
表1 各算法实验结果指标统计
4 结论
本文针对运动模糊图像,实现了基于低秩矩阵与稀疏约束的运动模糊图像盲复原,采用图像块的结构信息约束和稀疏约束作为图像先验信息,通过变量分离和交替迭代的方法求解目标函数方程。仿真实验表明,与具有代表性的运动模糊图像复原算法对比,本文的复原结果质量较高。
