灰色预测模型GM(1,1)的改进及应用
2021-05-11杨存典张雁王怡
杨存典 ,张雁,王怡
(1.商洛学院城乡规划与建筑工程学院,陕西商洛 726000;2.商洛学院经济管理学院,陕西商洛 726000)
灰色系统理论[1]是邓聚龙教授1982年提出的研究数据量小、信息贫瘠的不确定性问题的理论方法。灰色预测模型GM(1,1)是灰色系统理论的核心内容,通过已知的部分数据,将系统信息抽象量化,然后寻找最优化模型,并对未来数据进行预测[2]。该理论提出后一直受到人们的关注,在工业、农业、交通、经济等领域得到了广泛应用。然而,在灰色模型GM(1,1)预测过程中,出现了模型预测精度较低的情况。对此,杨华龙等[3]运用自动寻优定权和最小二乘法给出了改进预测模型,解决了原有模型中对背景值和初始值规定的不合理问题。何昕等[4]运用马尔可夫链理论对灰色GM(1,1)模型预测法进行了改进,解决了依靠灰色序列构造回归模型带来的误差,预测精度得到了改善。马维军[5]采用补充残差与加权平均的方法对灰色模型进行了改进,改进后的灰色预测模型精度较原始模型有所提高。任工昌等[6]通过对原始数据序列进行平滑处理,建立了新的灰色预测模型,并用此方法对电力负荷进行预测分析,提高了预测精度。程毛林[7]对灰色预测模型采用叠加三角函数多项式进行拟合,降低了误差,提高了精度。谭冠军[8]通过构造背景值表达式,使模型GM(1,1)适用于等间距和非等间距序列,扩大了GM(1,1)的适用范围。樊新海等[9]通过自动寻优定权的方法,改进了GM(1,1)模型背景值的选取。徐华锋等[10]、王健[11]、黄克[12]、郭金海等[13]、徐宁等[14]分别用不同方法对灰色模型进行优化,并提高了预测的精确度。综上所述,灰色预测模型GM(1,1)从提出到应用,很多学者在方法的改进和精度的提高方面做了大量的工作,但仍然存在初始值选取和背景值构造方面存在运算量过大,寻优参数等距增加而带来的局限性。本文运用最小二乘法,解决了上面所提到的问题,增加了灰色预测模型GM(1,1)应用的普遍性。
1 灰色预测模型GM(1,1)存在的问题
灰色预测模型GM(1,1)的建模过程是将无规律的原始数据进行1-AGO,减少数据的波动,得到规律性较强的生成数列后进行建模,运用模型进行预测,然后递减还原成原始序列。

若原始序列X(0)和一阶累加生成序列X(1)满足准光滑性检验:

则X(1)具有指数增长规律,灰色微分方程为:

其中,a称为发展灰数,b称为内生控制灰数,Z(1)(k)是紧邻均值,既

X(1)的白化微分方程为:
用最小二乘法拟合得到:
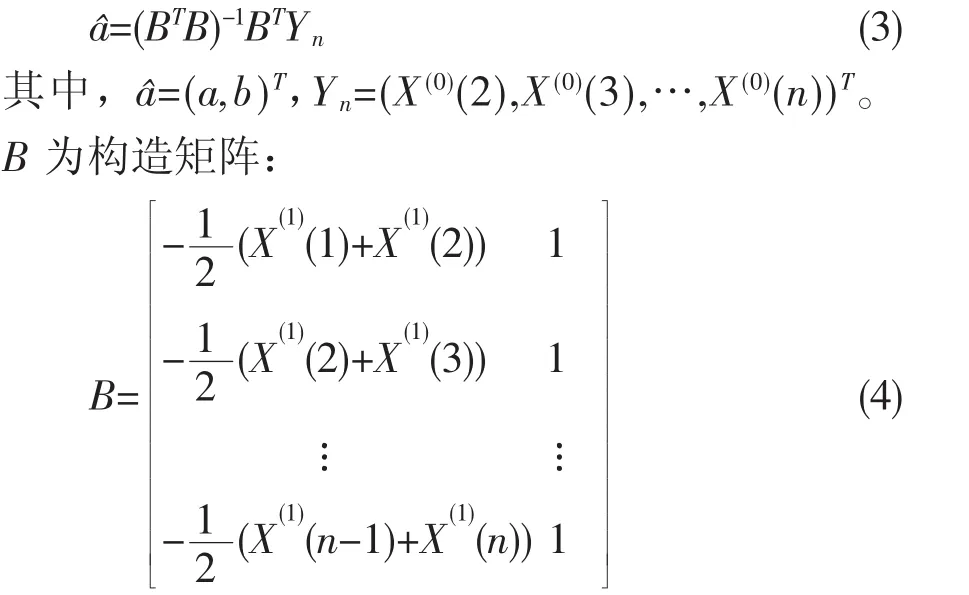
微分方程(2)所对应的事件响应函数为:
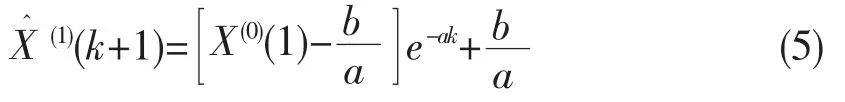
对(5)式递减还原,可以得到原始序列的灰色预测模型:
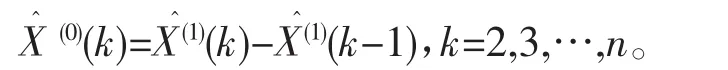
以上的建模过程存在的问题有三个:第一,必须进行准光滑性和指数规律的检验;第二,解微分方程的初始条件假设X(1)(1)=X(0)(1),认为拟合曲线一定经过初始点(1,X(1)(1)),实际上作为误差平方和最小的拟合曲线,并不一定通过初始点;第三,背景值用梯形的面积近似代替,即
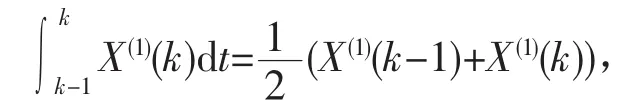
必然出现预测误差。
2 灰色预测模型GM(1,1)的改进
为了解决以上问题,按照1-AGO序列X(1)满足指数规律的要求,通过最小二乘法原理,找到指数方程中的参数估计,有效回避了初值的假设和背景值的近似计算。



有了参数p,q的估计值,就可以用X^(1)(t)=pe-at+q进行预测。
3 实例分析
根据商洛统计年鉴[14],商洛市2002—2011年房地产相关数据如表1所示。
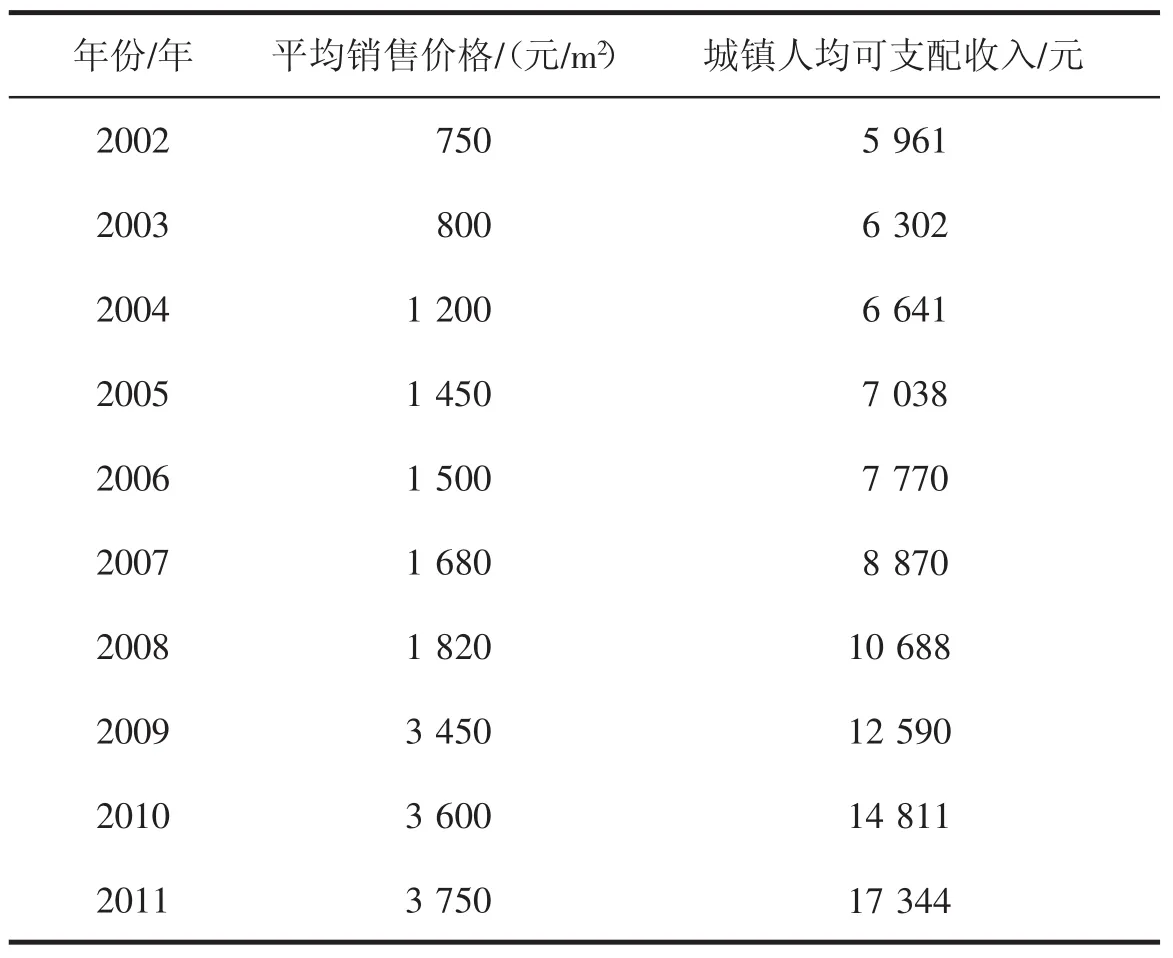
表1 2002-2011年商洛房地产市场价格及城镇人均收入
将平均销售价格进行处理,并作为原始数据序列:
X(0)={750,800,1200,1450,1500,1680,1820,3450,3600,3750}。
1-AGO序列是:
X(1)={750,1500,2750,4200,5700,7380,9200,12650,16250,20000}。
用MATLAB软件计算,由(3)式得:

根据改进后的预测模型计算得:
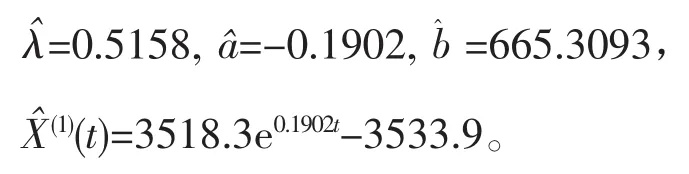
计算结果见表2及2002—2011年商洛市房地产市场价格趋势图(见图1)①。

表2 2002-2011年商洛房地产市场价格的预测值及绝对误差比较

图1 2002—2011年商洛市房地产市场价格趋势
计算原始数据序列的标准差:

计算相对序列的标准差:

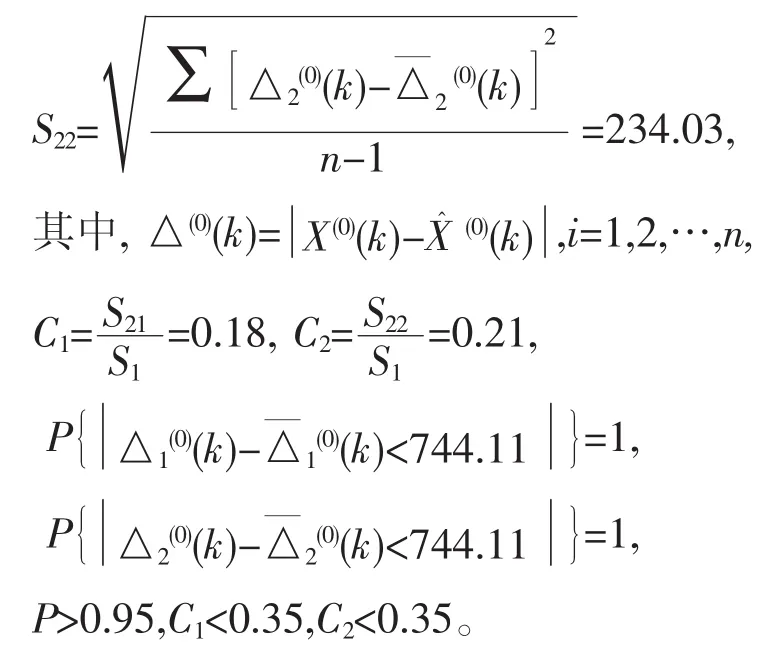
检验通过,预测精度达到精度要求。
4 结论
改进后的灰色预测GM(1,1)模型首先回避了初始条件X(1)(1)=X(0)(1)的假设,因为拟合曲线不一定经过X(0)(1)点;其次,把背景值由紧邻均值的近似计算进行了推广。通过实例分析,预测结果的相对误差由0.074 6提高到0.034 0,比原来的灰色预测GM(1,1)模型结果精度有所提高。
注释:
①表2及图1的预测数据来自作者承担的陕西省社科基金项目研究报告。
