一种多特征融合的特征匹配算法

李国祥,王继军,马文斌

(1.广西财经学院 教务处, 广西 南宁 530003; 2.广西师范大学 广西多源信息挖掘与安全重点实验室,广西 桂林 541004; 3.广西财经学院 信息与统计学院, 广西 南宁 530003)

图像匹配是机器视觉重要的组成部分,其主要作用是确定不同视角、光照等条件下的图像空间对应关系,广泛地应用于图像检索、目标追踪、遥感图像处理等领域。图像描述子是当前主要的图像匹配方法,通过对不同特征点描述子间的相似性测量,完成不同特征点之间的匹配。其中最著名的莫过于SIFT[1]算子,以及众多在此基础之上的各种改进算法。

PCA-SIFT[2]选定为以特征点为中心的41×41矩形,计算区域内水平、垂直方向的偏导数,形成该特征点3 042维的特征向量,计算图像所有特征向量的协方差矩阵,生成投影矩阵从而将特征向量降至K维,并显著地提升了SIFT的匹配性能。speeded up robust features(SURF)[3-4]对SIFT进行了有效改进,使用不同尺寸快速海森矩阵检测关键点,同时利用harr小波响应生成64维描述符,大幅提升了特征计算速度。Affine SIFT[5]是一种具备完全的仿射和尺度不变性的特征提取算法,不过其较高的计算复杂度,导致难以满足实时性的要求。另外还有各类基于核函数和混合核函数的特征描述子。BRIEF[6]提供了新的特征描述算法,当完成了特征点定位后，在领域块中随机挑选点对比较亮度值生成256位的二进制编码,但不具备旋转不变性。ORB[7]将特征点提取FAST算法和特征点描述BRIEF结合在一起,并改进了原BRIEF的旋转不变性,特征生成的速度大幅提升,但在尺度方面效果较差。

另外就是通过核函数的方式生成特征描述子。文献[8]通过核函数将图像映射至RKHS中的高维向量,通过向量内积完成2幅图像相似性的度量；文献[9]建立核函数描述子以笛卡尔坐标和极坐标,梯度模和梯度方向、梯度方向与极坐标角度差等特征信息为基础,通过傅里叶级数拟合将其映射为特征向量,最后使用克罗内克积形成新的特征向量。还有通过选择余弦核函数作为KPCA的映射核[10],对原SIFT向量降维至55维。

伴随着深度学习在语音识别、自然语言处理、计算机视觉、图像与视频分析、多媒体等诸多领域的应用取得成功,学者们提出了众多基于深度学习特征描述:DeepDesc[11]、TFeat[12]、LIFT[13],然而近年来的一些研究证明,并非深度学习特征完全优于传统特征描述,文献[14-15]通过大量的标准化对比实验,验证了深度学习可能没有比简单方法产生足够的额外效果,同时深度学习方法对于计算环境要求较高,在一定程度上限制了适用范围。

结合上述研究,本文回归至原始特征优化的层面,以广泛使用的SIFT算子为出发点,通过选择有效的核函数和简单易行的映射变换,构建一种可以适应复杂环境变换的特征描述子,大幅度降低特征维度。

1 图像核函数的空间映射

在图像识别领域,完备的图像特征对于大规模数据集带来了巨大存储和计算成本,原高维度特征的有效编码聚合,显得尤为重要。如Hamming Embedding[16]将原SIFT特征与聚类中心中值相减,形成新的64位二进制聚合编码,特征间的相似性测量就变成了二进制的或运算；Fisher Vectors[17]统计视觉词典与局部特征的差异,利用似然函数的梯度向量表达图像等。聚合编码本质在于单纯的特征点信息，一方面使得特征维度较高,另一方面特征点所具有的信息量并不含有典型可区分性信息,有时甚至是负面的,冗余的信息量对于识别匹配带来误判;通过特征聚合来生成简单具有代表性的特征表达。还有就是利用特征向量自身的数理特点,从中提取主成分。文献[18]使用PCA和白化对100 k词表直方图直接进行降维,效果显著;在原始特征的编码和降维基础上,文献[19]引入径向基核函数将图块映射为梯度、颜色和形状的特征描述；文献[20]使用Von Mises核函数完成角度向量的映射,结合上述思想,本文同样通过核函数实现特征空间映射、降低特征维度、保证点对的匹配精度。

设图像的特征向量集X={x1,…,xN},xi∈Rd,‖xi‖=1,Φ(xi)是特征向量xi在高维空间的映射,i=1,2,…,N。令Φ(X)={φ(x1)φ(x2) …φ(xN)}T,引入核函数:

K=Φ(X)Φ(X)T=

(1)

原始空间模型在高维空间映射后为:

Φ(X)Φ(X)Tμ=λμ

(2)

其中:μ为矩阵K的特征向量;λ为矩阵K的特征值;N为原始特征维度。左右两边同时乘以一个Φ(X)T后,有

(Φ(X)TΦ(X))Φ(X)Tμ=λΦ(X)Tμ

(3)

约简后的特征即为原始特征在归一化的前n个特征值对应特征向量上的投影，即

λ1≥λ2≥…≥λn

(4)

从而使得在低维度线性不可分的特征向量在高维空间变成线性可分,而高维空间中向量内积演变为核函数值。其中核函数及其参数的选择便成为了关键问题,理论上矩阵K是对称半正定的即可以作为核函数,比如常用的径向基核函数、多项式核函数等,而这些核函数的选择和优化有些需要样本数据多元正态分布[21],有些时间和空间复杂度较高,有些选择后的核函数其高维空间映射并非线性可分。考虑到一些核函数描述子通常转化为线性内积的形式,直接采用最简单的线性核函数，即

k(x,y)=xTy

(5)

为了验证线性内积核的简单有效,这里将其与常用的径向基核函数[19]、余弦核函数[10]进行对比,如图1、图2所示。

虽然径向基核函数在仿射变换上的表现优于其他核,但是其对于光照、模糊等变换鲁棒性较弱,关键是它的时间复杂度是简单线性核的近10倍,如要在大规模数据集中开展实时运算则比较困难，见表1所列,而余弦核函数对于仿射变换明显表现效果欠佳。

图1 Graffiti的不同核函数匹配

图2 Car的不同核函数匹配

表1 不同核函数的时间复杂度比较 s

2 集成的特征提取算法

文献[22]提出了RootSIFT、可区分的查询扩展和特征扩充3种简单的提高图像检索精度的方法。在特征描述子层面上,利用Hellinger kernel代替标准的Euclidean Distance进行SIFT特征点相似性测量,完成SIFT空间到RootSIFT的映射,该映射对于进一步的图像检索分类效果有明显的提升。通过与文献[14]大量对比试验证明了其特征的稳健性,因此为了形成可以有效应对复杂变换的特征,本文将其与核函数相结合,集成为一个新的低维度稳健特征向量，如图3所示。

设x、y为特征向量且‖x‖=1,‖y‖=1,则两者的欧式距离可以表示为:

D(x,y)2=‖x-y‖2=

‖x‖2+‖y‖2-2xTy

(6)

通过Hellinger映射:

(7)

对特征向量x、y取平方根,从而将相似性测量的Euclidean Distance映射至Hellinger Distance,将该过程称为Root，即

(8)

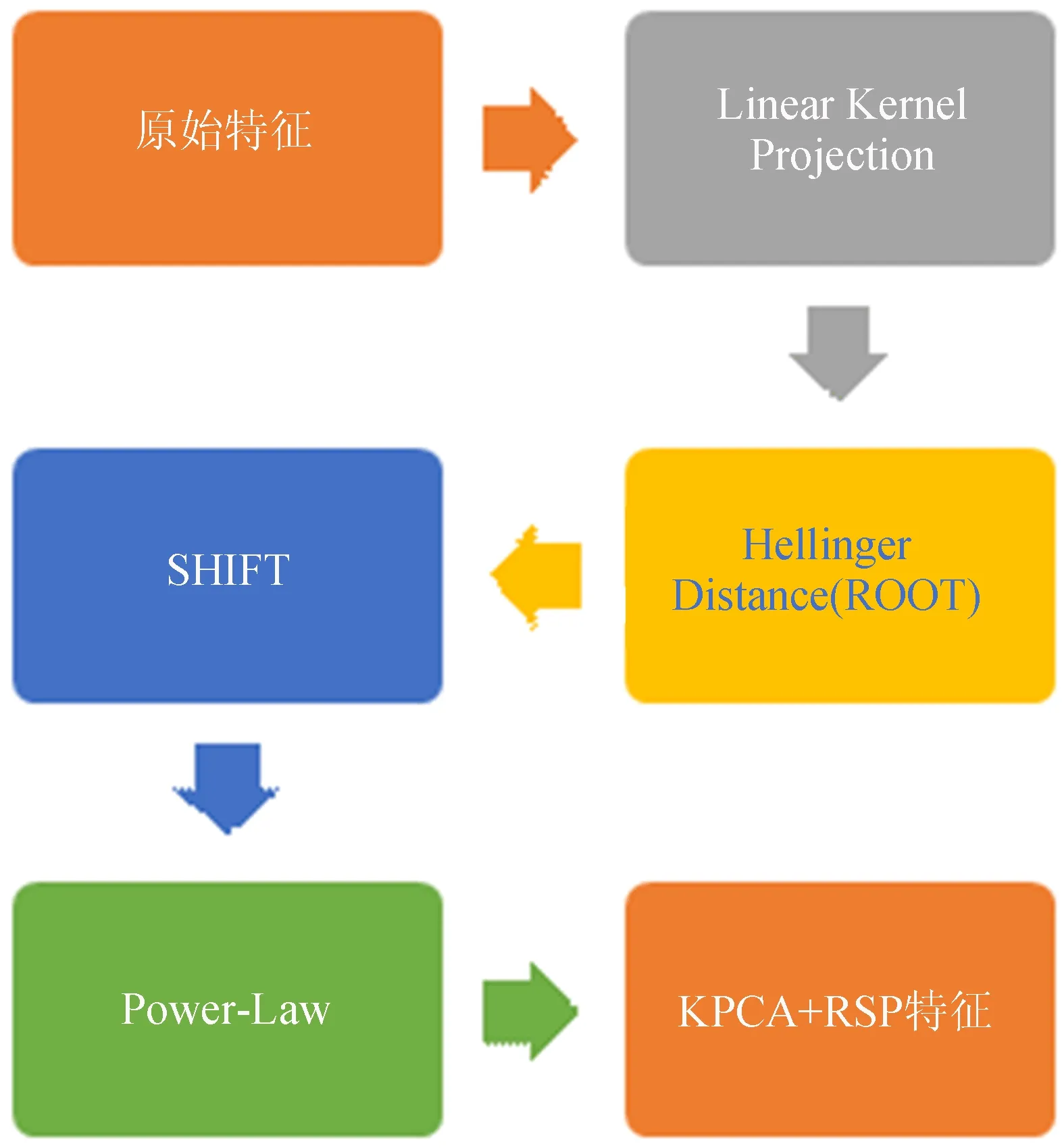
图3 集成特征的提取流程

由于通过线性核函数映射后的主成分包含负值,无法直接取平方根,这里将主成分最小值设为原点,将主成分向量在数轴上平移,使其相对距离保持不变。之后取平方根并对特征向量进行α中心化,仿照文献[23]将该过程称为Shift，即

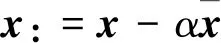
(9)

最后进行Power-law归一化,Power-law广泛地应用于BOW特征编码、聚合等的归一化[17-18,24],并对于特征表达有明显的提升。形成新的稳健特征向量，即

x:=sign(x)|x|β

(10)

3 实 验

为了验证集成描述子的有效性,这里实验数据库采用仿射、尺度等变换的Affine Covariant Regions Datasets以及复杂场景的Oxford Buliding。

(1) Affine Covariant Regions Datasets。该数据集中,本文选择仿射变换的Graffiti、模糊变换的bikes、尺度旋转变换的boat以及光照变换的cars 4类图像作为匹配图像。实验中首先使用最近邻距离和次近邻距离的比率作为特征点的初次选择,阈值为0.8。其次使用几何校验作为特征点的二次筛选。选择传统的SIFT和AS(Hessian Affine[25]SIFT)作为基本的特征描述子,在基本描述子基础上,本文提出的算法KPCA(linear)+RSP(Root+Shift+PowerLaw)分别与PCA、余弦核KPCA进行了对比实验，见表2所列。通过实验选取最优参数,α=0.95,β=1.2，令投影矩阵维度n=55,结果如图4所示,其中柱状图表示正确匹配的特征点数。

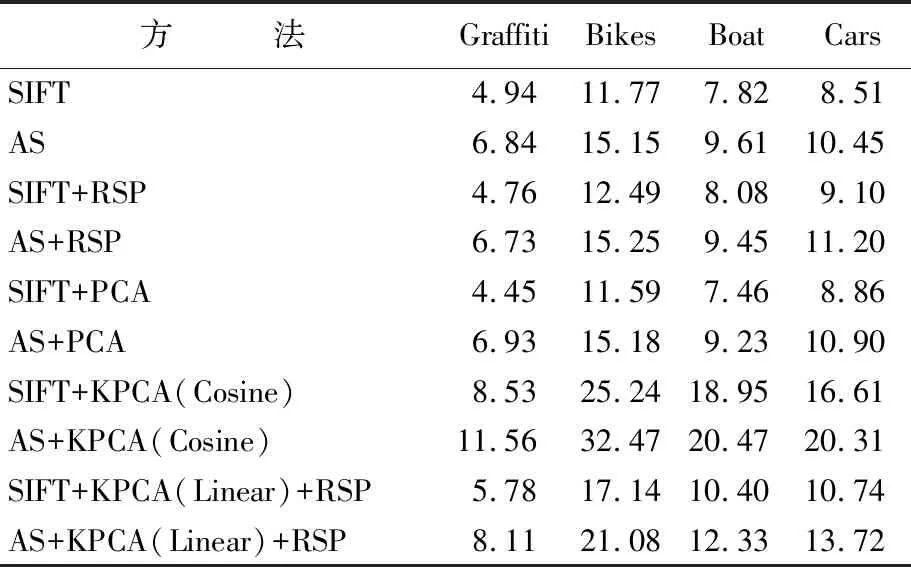
表2 时间复杂度对比 s

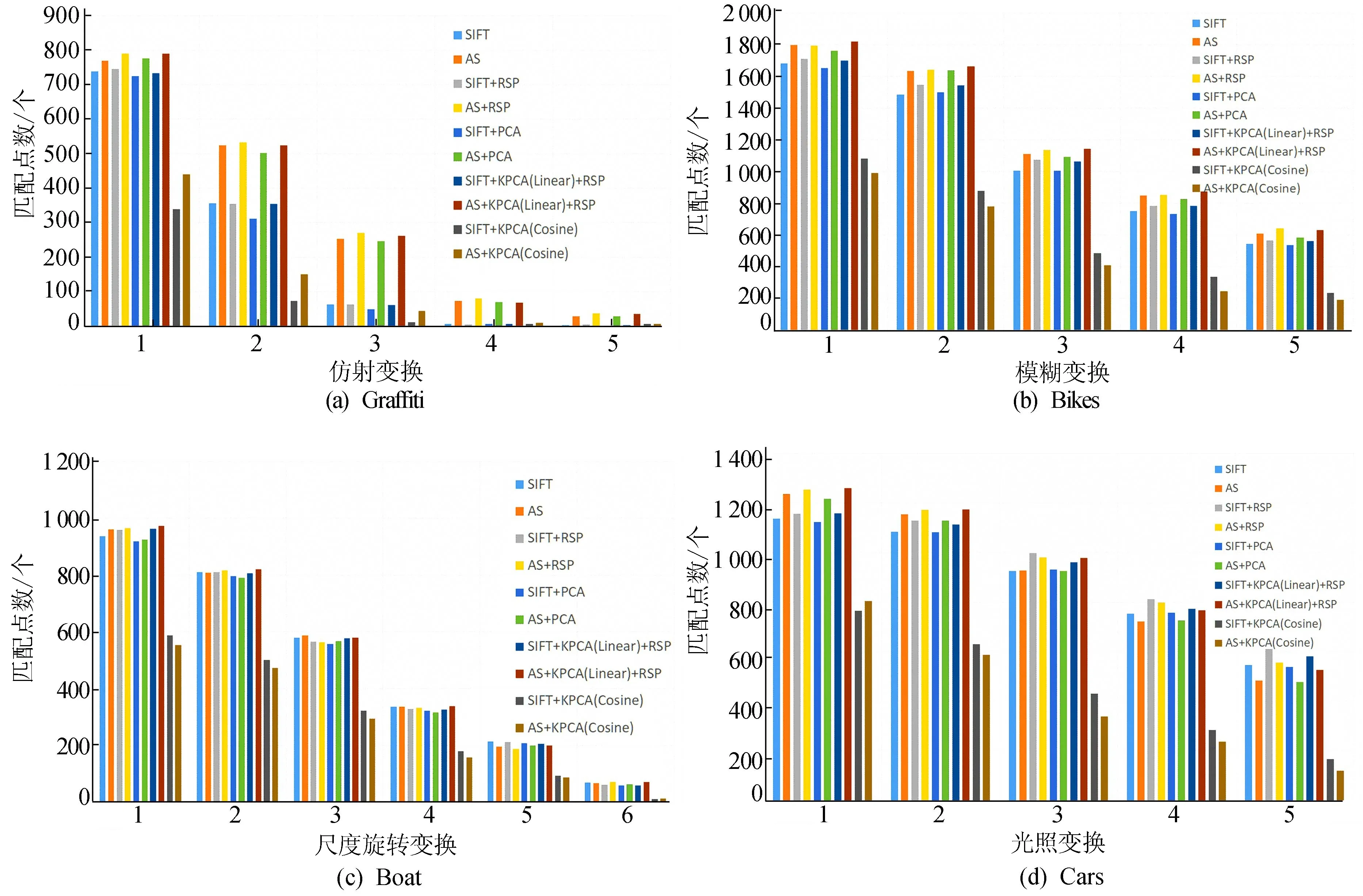
图4 Affine Covariant Regions Datasets 匹配点对数量图

根据上述实验可以看出,除了仿射变换Graffiti中SIFT和AS匹配效果有明显的差异外,其他3类图像两者效果基本相同,而且原始方法与RSP的集成,都在一定程度上提升了描述子的稳健性,说明了RSP的处理方法显著有效,本文所集成的线性核降维+RSP算法则略高于同类算法或与其持平,而非线性的余弦核函数匹配的特征点数量相对下降,且计算时间增加明显。

(2) Oxford Buliding。为了验证各算法在复杂变换环境下,特征算子的鲁棒性,选择图像检索领域中经常使用的Oxford Buliding数据集。该数据集包含10类建筑,并根据标的物在图像中的效果分别标记为good、ok、junk和bad。鉴于对特征稳健性的验证,实验中使用query作为原始图像,仅和ok标记图片进行匹配,ok标记代表了标的物在图像中呈现度大于25%,包含了各种复杂的视觉、尺度等变换。junk是标的物对象少于25%可见的图像,对于图像特征点匹配来说,即便人工标注部分图像也难以分辨。bad图像则与标的物不相关。为了应对场景中的复杂仿射变换,实验中使用Hessian Affine SIFT作为特征提取算子,选择数据集ok列表中前6副图像,共计50副图像作对比。

图5 All Souls 类别中ok标记图像的匹配效果

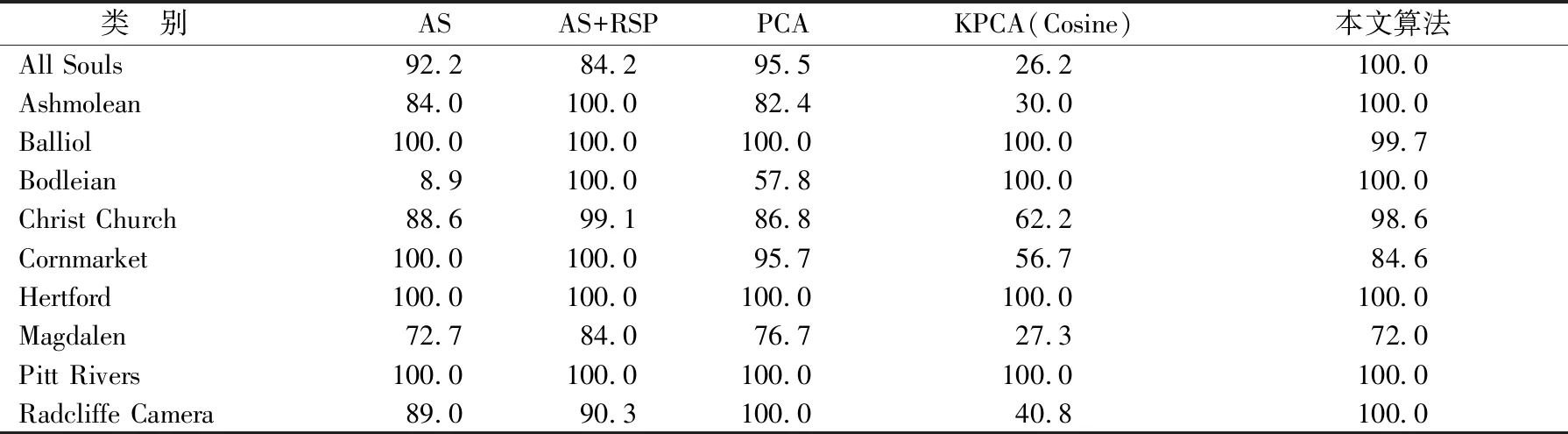
表3 匹配准确率对比表%

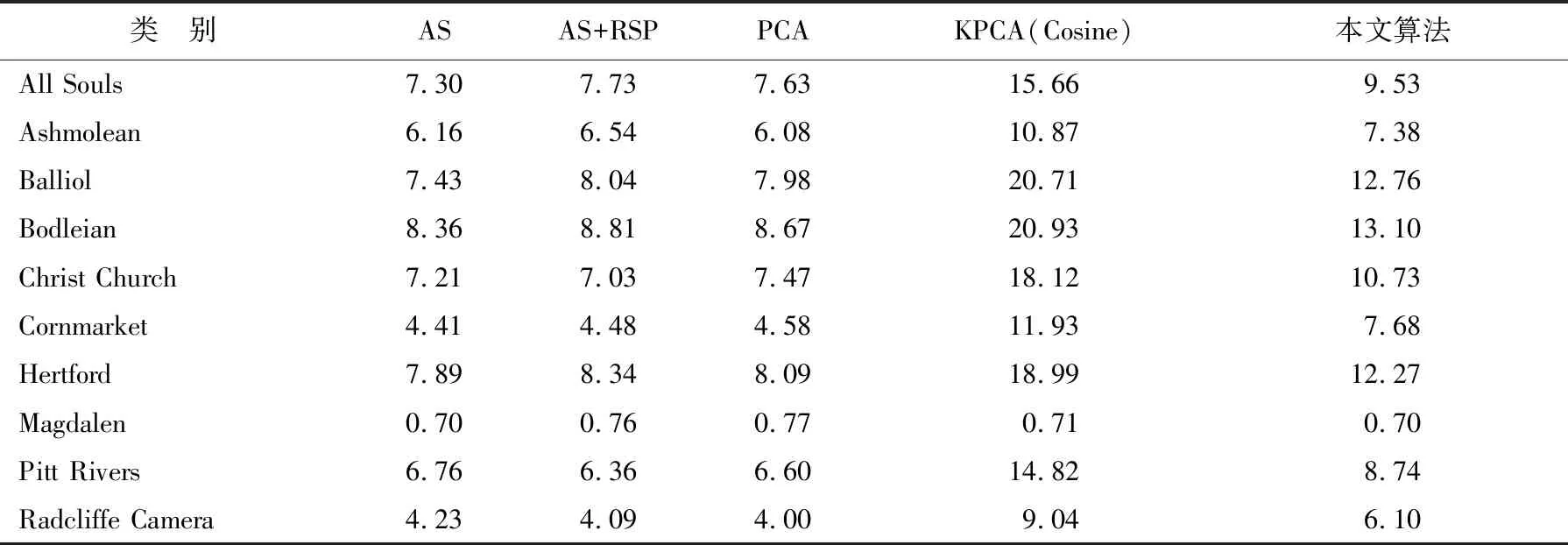
表4 时间复杂度对比表 s

通过对比可以发现,相对于其他方法,AS+RSP和本文方法能够在复杂变换的环境中保证特征点的匹配精度,证明了RSP的确能在一定程度上保证特征稳健。而线性核KPCA与之结合,在仅增加简单计算的基础上,通过设置投影矩阵维度,使得特征维度由原来的128维约简至55维,契合了大数据集时间和空间的实时性要求。AS、PCA和余弦核KPCA对于复杂变换表现不够稳定,部分特征出现局部最小值导致误匹配增加。

4 结 论

特征描述子的提取作为匹配的重要内容,除了要具备基本的仿射、尺度、旋转等不变性外,还要能够在复杂场景中保证相对的稳定。本文结合当前众多文献的研究方法,从简单易行、特征维度的降低和特征稳健3个方面,提出一种多特征融合的匹配算法。利用线性内积核映射原特征至高维空间提取主成分,减少特征冗余,解决特征维度过高的问题;利用Root、Shift和PowerLaw,在Hellinger空间对主成分平移和归一化,解决特征稳健性的问题。实验证明,相对于其他同类算法,该方法的匹配精度得到一定的提高,且鲁棒性较强。