子午线轮胎周向花纹沟共振频率预测方法

蔡青青,张永斌

(合肥工业大学 机械工程学院,安徽 合肥 230009)

0 引 言

随着汽车工业技术不断发展以及新能源汽车的普及,汽车的发动机、传动系统等噪声问题得到很大的改善,因此汽车轮胎噪声显得尤为突出[1],轮胎噪声已经成为汽车噪声的主要部分。轮胎噪声按机理主要分为轮胎振动噪声、空气动力学噪声以及花纹沟共振噪声[2]。以轿车为例,子午线轮胎是轿车常用的轮胎,汽车行驶时,轮胎表面的周向花纹沟与地面接触会形成一个两端均为开口的声学管道, 当外界的声音进入该管道时,与管道共振频率相同的声波会在该管道内形成驻波,这种由于共振产生的噪声称为轮胎花纹沟共振噪声。该共振噪声声压级较大,是轮胎噪声的重要组成部分。这个特定的频率与汽车行驶速度无关,只与花纹沟尺寸以及接地区域长度有关。周向花纹沟共振噪声一般固定出现在1 000 Hz左右。研究表明,乘用车噪声能量主要集中在800～1 200 Hz,而在这部分噪声中,轮胎周向花纹沟共振噪声占了很大比重。

通过错开花纹沟共振频率或运用亥姆霍兹共鸣消声器[3]等方法对管共振噪声进行降噪设计等措施都需要对花纹沟管道共振频率有较精准的预测,而针对轮胎花纹沟与地面形成的管道,其理论模型还未提出,管端修正还不够完善。

计算开口管声管共振频率的经验公式为:

(1)

其中,Δl为管端修正。

国内外现阶段对该管共振噪声频率预测运用的管端修正还局限于开口于自由场的圆管[4]Δl=0.6r和开口于无限大障板的圆管[5]Δl=0.85r,或通过实验测得，而关于汽车轮胎花纹沟管道的管端修正理论研究较少。实验研究结果表明,上述2种管端修正的计算结果比实际测量结果偏大。因此,有必要对轮胎花纹沟管端修正进一步优化。

1 轮胎/地面模型共振频率的推导

1.1 轮胎/地面模型的提出

根据对声管共振机理深入研究得知，管端修正是管口辐射阻抗引起的[6]。声源在管中传播时,管口会向外界辐射声波,即把管口看成声源；声源向外界辐射声波时,声源也会受到其产生的声场的反作用，即管口的辐射阻抗。辐射阻抗的辐射抗部分相当于增加声源表面的振动质量,即由于辐射抗Xr的存在,相当于有质量为Mr=Xr/ω的媒质黏附在声源上,随声源一起振动,这部分质量称为同振质量；同时使得管的有效长度比实际长度增加了Δl=Mr/(πr2ρ0),Δl称为管端修正。

实际上,子午线轮胎的周向花纹沟与地面形成的开口管的管口并不是开口于自由场。一方面,轮胎表面对管口声源辐射的声波具有反射作用;另一方面,地面对声音也具有反射作用。两者都会对管口的辐射阻抗产生影响,进而影响管端修正和管共振频率。地面可看成无限大刚性面,轮胎表面是一个较大的圆柱面,实际上的管端声阻抗的计算相当复杂,只能通过简化的方式进行近似计算。

本文提出描述轮胎花纹沟共振的“轮胎/地面模型”,如图1所示,即将胎面看成声学中的无限大障板。

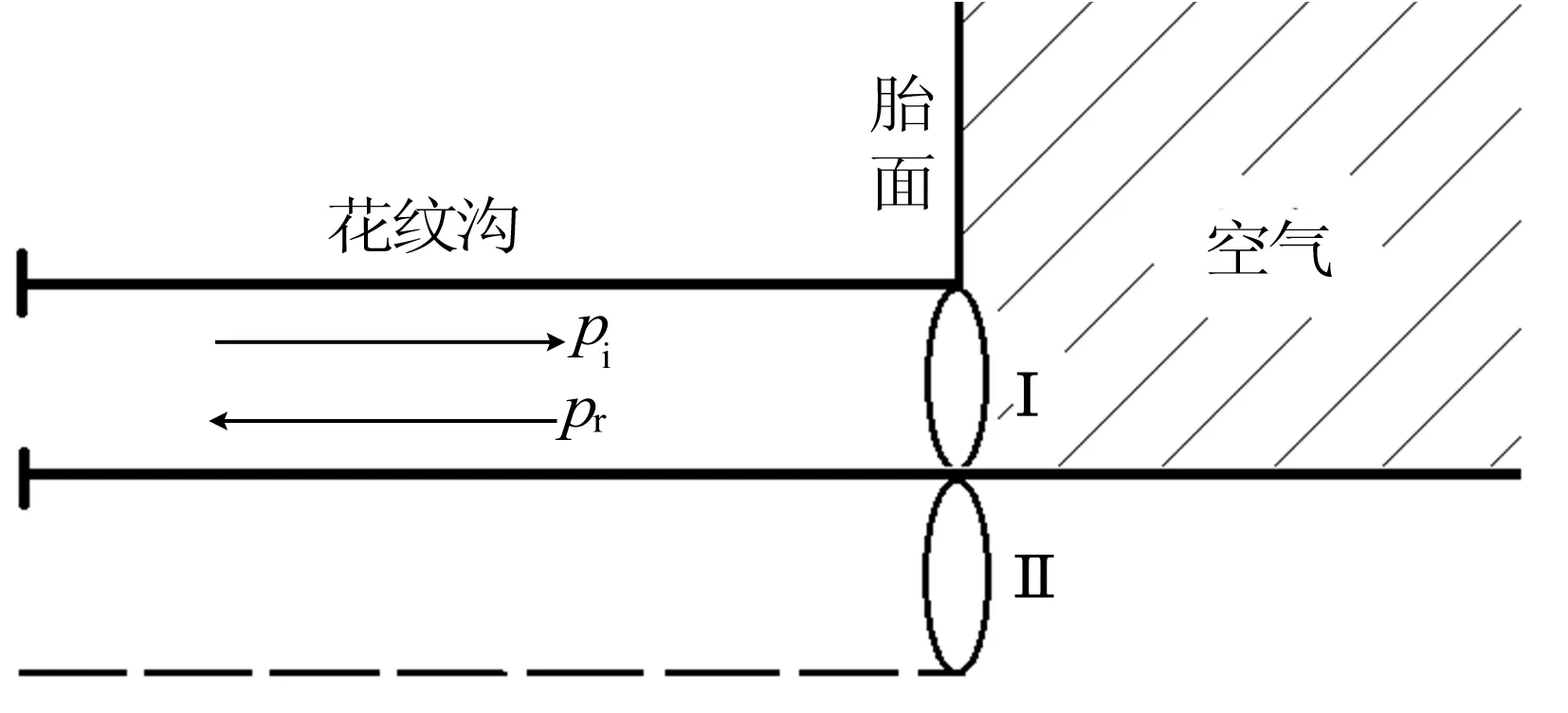
图1 轮胎/地面模型

1.2 管端修正及共振频率的计算

根据镜像原理,即当一声源靠近刚性面时,由于刚性面对声波的反射作用,使得声源向周围媒质辐射声波的情况与在自由空间条件下不一样,此时的辐射相当于它本身以及关于刚性面对称的“虚声源”组成的“组合”声源的辐射。

轮胎/地面形成的花纹沟管道如图2 所示。管口Ⅰ位于刚性面附近,根据镜像原理,靠近刚性面的管口声源Ⅰ向外辐射声波等于管口Ⅰ与管口Ⅰ关于刚性地面对称的虚声源Ⅱ辐射声波之和。

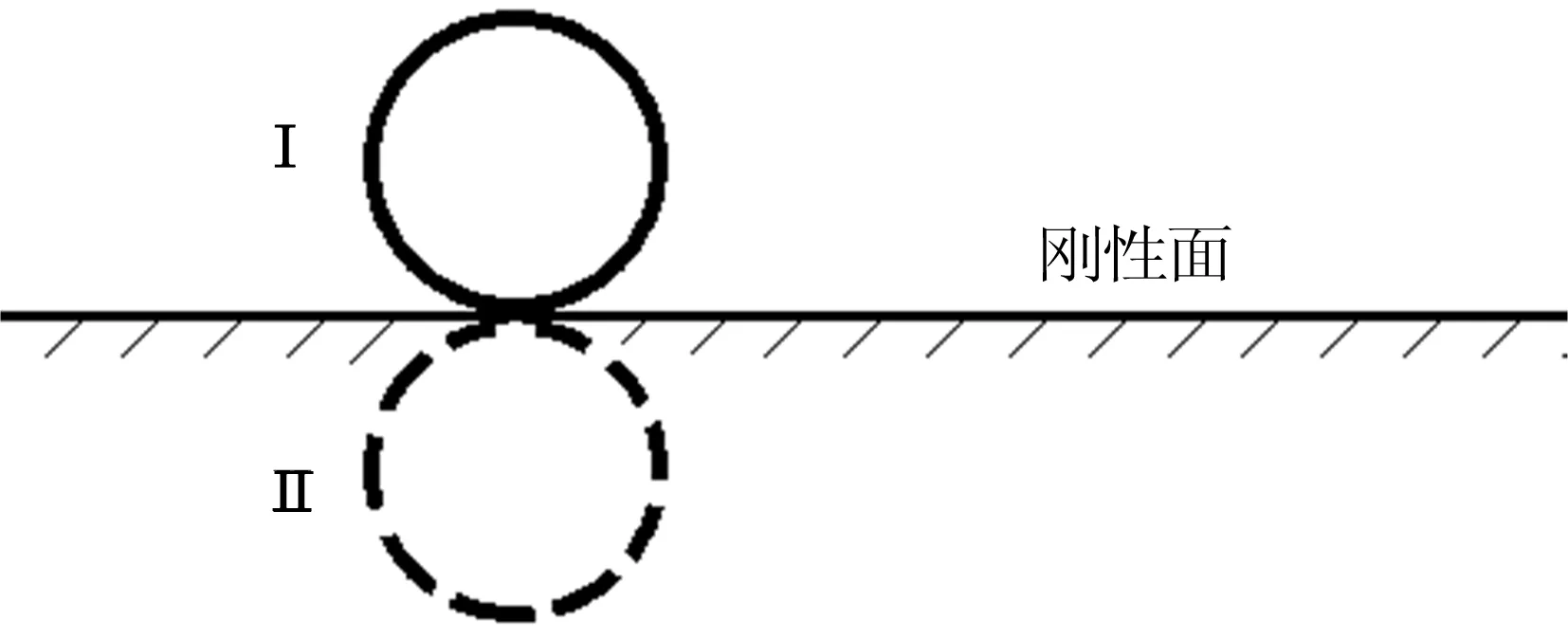
图2 管口及虚声源示意图

2个嵌于无限大障板的声源如图3所示。图3中嵌于无限大障板上的圆形活塞声源Ⅰ与声源Ⅱ声源大小、形状相同,均做同频率、同相位、同振幅的振动,声源平面位于yOz平面内,且中心位于y轴上,关于z轴对称分布,声源半径为a,2个圆形声源中心距离为d。

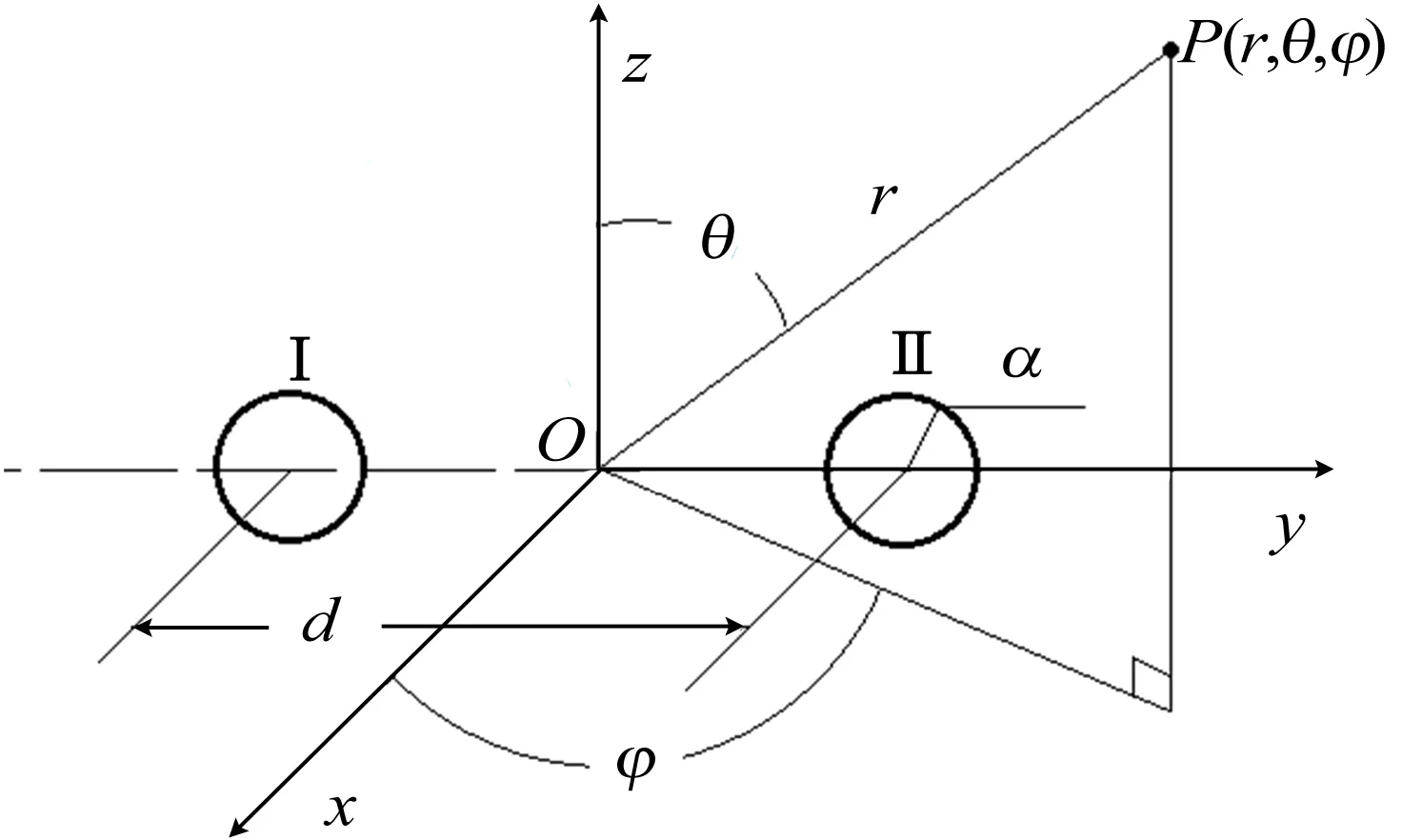
图3 2个嵌于无限大障板的声源示意图

在计算辐射阻抗时,利用辐射阻抗的定义计算声源表面受力会遇到积分难以求解的数学问题。文献[7]给出了图3中声源Ⅰ与声源Ⅱ组成的组合声源的总辐射阻抗,即

sinθdθdφ

(2)

其中:ρ0c0为声特征阻抗;S为声源总面积;λ为声波波长;K(θ,φ)为声源指向特性函数。

K(θ,φ)可以表示为:

(3)

其中，J1为一阶第一类Bessel函数[8]。

将(3)式代入(2)式,即得声源Ⅰ与声源Ⅱ组成的组合声源的总辐射阻抗,即

(4)

对轮胎/地面模型中管道末端Ⅰ进行受力分析可知,声源Ⅰ受到其自辐射力和虚像对其互辐射力,即f1=Z11v1+Z12v2,其中v1=v2,则有:

Z1=f1/v1=Z11+Z12=Z0/2

(5)

对(4)式求解得声源Ⅰ的总辐射阻抗为:

[1+cos(kdsinθsinφ)]sinθdθdφ

(6)

根据Bessel函数[8]性质,对(6)式进行化简可得:

[1+J0(kdsinθ)]sinθdθ

(7)

在(7)式中,互辐射阻抗Z12的部分可以用Bessel函数积分[9]写成如下形式,即

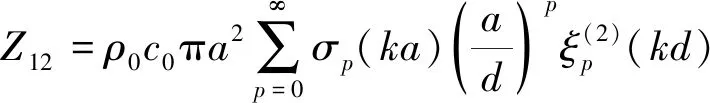
(8)

其中

σ1(ka)=2J1(ka)J2(ka),

(9)

(10)

(10)式中H函数为Struve函数,以无穷级数形式[10]表示如下:

(11)

将(9)～(11)代入(7)式,其中d=2a,则声源Ⅰ辐射阻抗为:

(12)

根据(12)式,可知声源Ⅰ辐射阻抗的的声抗部分为:

jX1≈

(13)

因为ka≪1,所以sin(ka)≈0,cos(ka)≈1;管端声抗部分相当于增加了管的长度Δl,满足:

V=Δlρ0πa2=Xr/ω

(14)

即可求得管的单端管端修正为:

Δl≈

a=1.12a

(15)

对于两端均开口的轮胎/地面模型,由于两端均向外界辐射声波,管的两端管端修正都要考虑在内,则总管端修正为Δl≈2×1.12a=2.24a,即理论共振频率为:

(16)

2 声管共振实验

以精加工的黄铜管作为声管、塑料障板作为无限大障板在半消声室中做声管共振模拟实验,轮胎/地面模型实验的模拟和实物图如图4所示。

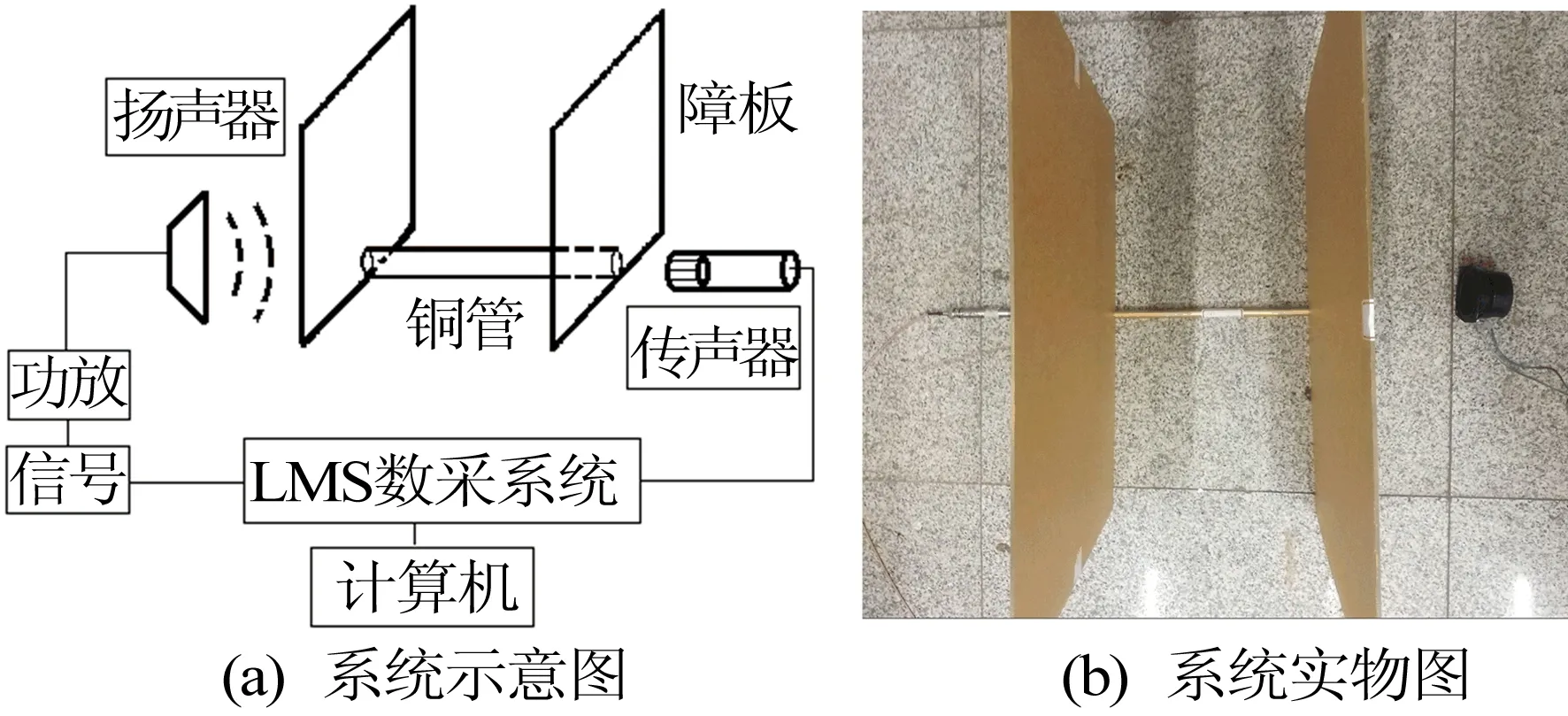
图4 安装完成的实验系统示意图和实物图

图4中,铜管横放于地面上,用地面模拟真实的路面,用障板模拟轮胎表面。

实验中声源是扬声器,采用的声信号为扫频信号,信号由LMS数采系统输出,并通过功率放大器进行放大。

由于扬声器与传声器表面具有一定的几何结构,会对管口的声波起反射作用,改变原有的管口辐射阻抗,进而影响管端修正和共振频率。因此,在实验能测得较明显的共振峰值的条件下尽可能使扬声器与传声器远离管口,以减小实验的系统误差。

分别进行以下2组实验:

(1) 管的内径为11.3 mm,管长变化。

(2) 管的长度均为140 mm,管径变化。

经过多次测量,求得平均共振频率以及按实测共振频率计算出管端修正Δl,见表1所列。

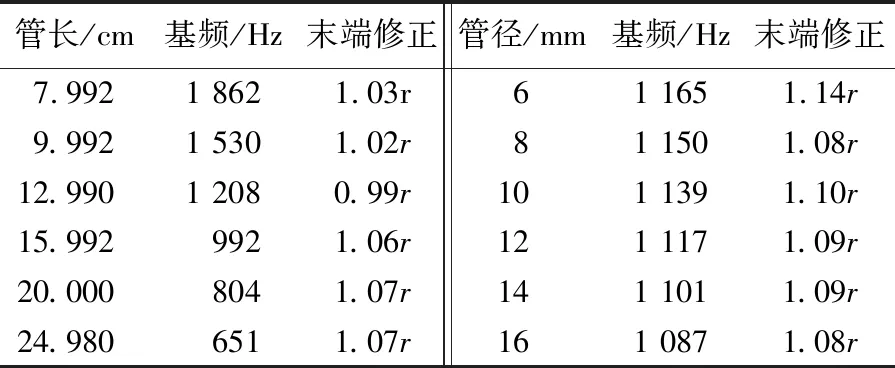
表1 实测共振频率以及计算出的管端修正

从表1可以看出,声管共振的管端修正可近似为常数,且与理论推导的管端修正Δl=1.12r接近。

3 子午线轮胎周向花纹沟共振实验

此次实验目的是测出子午线轮胎花纹块与地面接触形成的单个声管的管共振频率。实验中的轮胎是测试专用轮胎。实际花纹沟管共振噪声是汽车在行驶时产生的,轮胎行驶的路面可能会有高低起伏,引起汽车超重或失重,进而使得花纹沟的实际接地长度、有效深度增加或者减小,导致共振频率有所波动,这些在实际中应考虑在内。

本文采用静态的理想模型,参考常见汽车轮胎的载荷,并用螺旋挂钩将载荷施加到测试轮胎中心轴上,加载并测量出轮胎花纹沟接地长度。安装加载后的实验装置如图5所示。实验测试原理和方法与声管共振实验相似。

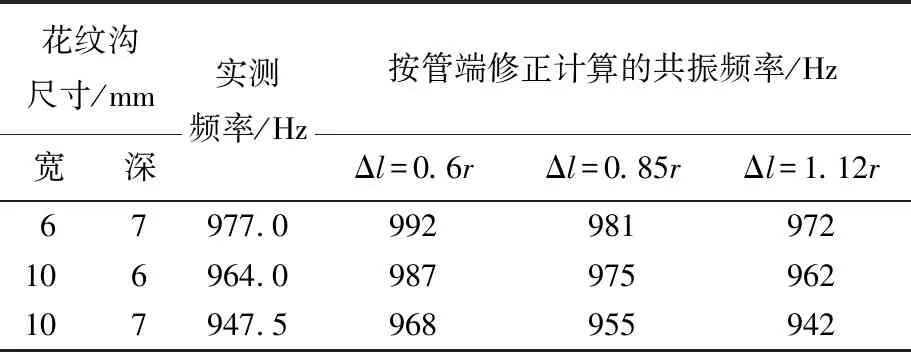
分别对宽6mm深7 mm、宽10 mm深6 mm、宽10 mm深7 mm的花纹沟进行实验。经过多次实验,将实验实测结果与按各种理论模型计算出的共振频率进行对比，结果见表2所列。

为计算方便,这里用圆管来等效近似实际上的矩形截面的花纹沟管。

图5 轮胎声管共振噪声测试装置

设等效半径为r,实际矩形截面的长和宽分别为a、b,则等效半径为:

(17)

从表2可以看出,按轮胎/地面模型计算出的共振频率比按管端修正Δl=0.6r、Δl=0.85r计算出的频率更接近实测值,精度更高。

4 结 论

本文提出了描述子午线轮胎周向花纹沟声学开口情况的轮胎/地面模型,从声学的角度推导出该模型的管端修正和共振频率,并通过声管共振实验与花纹沟共振实验验证其正确性,得出结论:本文提出的轮胎/地面模型推导出的共振频率比现有公式的计算精度更高,可为子午线轮胎周向花纹沟共振频率的预测提供参考。